水培作物生长所需营养液投放周期模型

于淑妹，杨俊仙*，曹宗宏

（安徽农业大学 理学院 a.应用数学系；b.应用数学研究所，安徽 合肥230036）

水培作物生长所需营养液投放周期模型

于淑妹a，b，杨俊仙a，b*，曹宗宏a，b

（安徽农业大学 理学院 a.应用数学系；b.应用数学研究所，安徽 合肥230036）

为了水培作物更加健康快速的生长，同时又考虑到营养液的成本，将普遍采用的一次性投放足够量的营养液转变为分时分阶段的投放。在此基础上建立两个阶段的数学模型，即作物定植前在基质中仅靠水源生长阶段，以及定植后投入一定量一定浓度的营养液后的生长阶段。最后以水培意大利生菜为例，测量出各阶段开展度的数据，并用Matlab给出时间与作物生长量之间关系的图像。

营养液；周期；模型

随着我国设施农业的发展，无土栽培特别是水培技术得到广泛的推广和应用。蔬菜水培可避免土壤栽培中容易出现的连作障碍，栽培条件易于控制，蔬菜生长整齐，周期短，而且清洁无污染，可多茬栽培，连续生产，均衡上市，具有很高的商业价值。

近几年兴起的家庭菜园方式种植植株一般会选择直接从市场购入配好的标准浓度的营养液，按说明一次性加入充足的营养液至定植后的植株中，这样的方式简易、好操作，但从节约成本，提高效率方面来说并非最优。一方面地下水水源中Ca和Mg的含量均接近和超出园试配方的浓度［1］，可充分利用其中的有用的营养元素；另一方面，若可以分次添加由低到高不同浓度的营养液，可减少营养液使用的总量，最终达到节约成本的目的。

可以查阅到的资料［4-8］以介绍水培作物具体的播种、分苗、定植方法以及如何配制适当浓度的营养液较为常见，而利用数学方法定量分析营养液的投放周期尚少见到。本文受到文献［2，9，10］的启发，建立微分方程模型，较精准地预测投放营养液的周期，对成长期较短的植株如生菜，我们可以计算出成熟期，而对成长期较长的植株如黄瓜、草莓等该周期即为分次投放营养液的时间间隔。

最后以意大利生菜在实验室条件下用充气式静止营养液培养方式，以开展度为测定目标，得出数据，并以Matlab给出时间与作物生长量间的关系图像，进一步验证了建立的数学模型的合理性。

1　建立模型

本文主要研究随着营养液的投入植物生长量随时间变化而变化的关系，这与众所周知的生物种群的变化动态可用Logistic模型［3］来描述不同。无论是第一阶段定植前作物仅靠基质中水源自身的营养而生长的阶段，还是第二阶段定植后加入适当浓度的营养液后的生长阶段，植物生长速率总是经过由快变缓的过程，最终目标是给出理论上的数值，控制再次投放营养液的时间［11，12］。

1.1第一阶段

水培作物定植前，用x代表其生长量，记r1为自然增长率系数，N为自然状态下的环境容纳量，t0为作物在基质中出苗时刻即开始观测时刻，t1为定植时刻，为了简化模型忽略作物定植与第一次投入营养液之间的时间间隔，因此，t1即为第一次投入营养液的时刻，ε＞0为给定的一个参数，表明某时刻的生长量的变化率。作物种子在基质中，仅靠水源及周围适宜的温度就可以保持短期增长趋势，当作物的生长速率减缓到ε时，即此时为t1时刻，则开始定植，随后第一次投放营养液。

1.2第二阶段

第一次投放营养液后，一段时间内作物营养充足快速生长，但随着时间推移，营养液中主要营养成分耗散，作物生长变缓，从而需要再次投放营养液。记ti为第i次投放营养液的时刻，i=1，2，…，m为加入营养液条件下环境容纳量，T为两次投放时间间隔。

2　模型求解

对于第一阶段的模型，欲求解

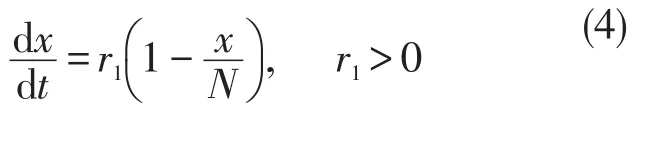
先求

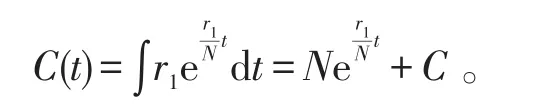
因此，（1）的通解为

将条件x（）t0=x0代入（6）可得

从而可得（1）的特解为

由（7）和（9），可得

即有

类似地，对于第二阶段的模型，欲求解（3）在条件（4）下的解，先对（3）用常数变易法然后使用条件（4），可得

3用MATLAB仿真

3.1实验

实验室条件下，用充气式静止营养液培养方式种植5株意大利生菜，营养液选用标准浓度的日本山崎配方。2015年9月5日，将蛭石用清水浸透，将生菜种子撒播于其中，9月8日出苗，开始每3日测量其开展度，生长变化率明显变缓后考虑分苗、定植，为了简化过程，忽略分苗与定植间的时间间隔。定植后投入标准浓度山崎溶液，每3日测其开展度，把测得的数据（见表1）取平均值描点得到生菜生长折线图，如图1所示。

图1　生菜生长折线图

表1　菜生长测量数据

3.2参数拟合

先确定模型（1）（2）中的参数，由专业知识可知 N=5，r1=2.28，再由表 1中的数据易知x0=1.12，t0=1，给定 ε=0.1，由（6）式可求出t1=7.33≈7天。

再确定模型（3）（4）中的参数，结合表1中的数据利用 SAS软件，易知 m=32，r2=3.1，α=0.02，最后将以上参数代入（7）式得：T=32.51≈33天。

3.3分析

用Matlab仿真的生菜生长图，如图2所示。从图2曲线态势看基本符合图1的意大利生菜的生长态势，图2中曲线明显的跳跃即为定植时机，随后添加营养液，之后进入一个由快渐缓的生长期直至成熟。

图2　生菜生长matlab仿真图

4　结束语

本文基于投放营养液前后水培作物的生长变化规律，建立营养液投放周期模型。若作物的生长期较短，所求周期T即为作物上市期，若生长期较长，则为多次投放营养液时，每两次间的时间间隔，对于较准确的预测、控制作物成熟期并减少营养液的用量有一定的意义，而所求定植时刻t1，将通过观察作物叶片特征选择定植时机转化为定量分析的方法，理论上更精确，最后，实验室条件下得出的数据与Matlab作出图像拟合较好。分阶段投放营养液时由于作物处在不同的生长期而导致营养液投放周期会有所变化，是否可将作物生长分为若干阶段更精确的给出周期T是今后讨论的方向。

［1］ 牟咏花，张德威，程前，等.利用地下水进行生菜无土栽培的营养液配方研究［J］.浙江农业科学，1996，18（3）：132-135.

［2］ 程述汉，徐臣善，李明，等.作物害虫化学防治的数学模型［J］.农业工程学报，2008，24（s2）：32-35.

［3］ 陈兰荪.数学生态模型与研究方法［M］.北京：科学出版社，1988：58-77.

［4］Tang S Y，Chen L S.Modelling and analysis of integrated pest management strategy［J］.Discrete and Continuous Dynamical Systems，Series B，2004，4（3）：759-768.

［5］ 张树文，陈兰荪.具有脉冲效应和综合害虫控制的捕食系统［J］.系统科学与数学，2005，25（3）：264-275.

［6］ 祝光湖，陈兰荪.脉冲治理害虫在一个新的生态-传染病模型中的应用［J］.福建师范大学学报（自然科学版），2009，25（3）：19-25.

［7］ Li B，Liu B P，Yu R R，et al.Bacterial brown stripe of rice in soil-less culture system caused by Acidovorax avenae subsp avenae in China［J］.Journal of General Plant Pathology，2011，77（1）：64-67.

［8］ Silberbush M，Ben-Asher J，Ephrath J E.A model for nutrient and water flow and their uptake by plants grown in a soilless culture［J］.Plant and Soil，2005，271 （1/2）：309-319.

［9］ 杨俊仙，于淑妹，闫萍，等.营养液对植物影响的数学模型的全局稳定性［J］.生物数学学报，2012，27 （4）：657-662.

［10］杨俊仙，闫萍.一类具饱和发生率的时滞SEIR传染病模型的分析［J］.中山大学学报（自然科学版），2015，53（3）：51-55.

［11］杨俊仙，徐丽.一类具非线性发生率的SIQS传染病模型的动力学性态分析［J］.浙江大学学报（理学版），2015，42（3）：271-275.

［12］杨俊仙，徐丽.一类具非线性发生率和时滞的SIQS传染病模型的全局稳定性［J］.山东大学学报（理学版），2014，49（5）：67-74.

Cycle model of sprinkling the required nutrition liquid for growth of hydroponic crop

YU Shu-meia，b，YANG Jun-xiana，b*，CAO Zong-honga，b

（a.Department of Applied Mathematics；b.Institute of Applied Mathematics，School of Science，Anhui Agricultural University，Hefei Anhui 230036，China）

A time-phased sprinkling is adopted instead of a disposable sprinkling sufficient amount of nutrient solution in order to make hydroponic crop grow more healthily and rapidly，and regarding the cost of nutrient solution.The mathematical model of two phase is established on its basis，namely growth phase on crop abutting the water when transplanting，as well as the growth phase on a certain amount and a certain concentration of nutrient solution.Finally taking Italy Hydroponic Lettuce as an example，measure data of their development，then draw its relationship image between time and crop growth with the help of Matlab.

nutrition liquid；cycle；model

O175.1

A

1004-4329（2016）02-024-04

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）02-024-04

2015-12-15

国家自然科学基金项目（11201002）；安徽农业大学校级质量工程项目（2015039）资助。

于淑妹（1983－），女，硕士，讲师，研究方向：微分方程与应用。

杨俊仙（1976－），女，硕士，副教授，研究方向：微分方程与应用。Email：yangjunxian@ahau.edu.cn。