基于改进偏互信息的火电厂SCR脱硝系统建模
秦天牧, 刘吉臻, 方连航, 刘红岩, 杨婷婷, 吕 游
(1. 华北电力大学 控制与计算机工程学院,新能源电力系统国家重点实验室,北京 102206;2. 海南电力技术研究院,海口 570203)
基于改进偏互信息的火电厂SCR脱硝系统建模
秦天牧1,刘吉臻1,方连航2,刘红岩2,杨婷婷1,吕游1
(1. 华北电力大学 控制与计算机工程学院,新能源电力系统国家重点实验室,北京 102206;2. 海南电力技术研究院,海口 570203)
由于传统偏互信息(PMI) 法利用条件期望计算回归值时计算误差较大,会对筛选正确率产生不利影响,将插值法应用于回归值的计算,提出了改进偏互信息(IPMI)法并利用Benchmark验证方法的有效性.将IPMI法应用于火电厂SCR脱硝系统,选取出最优变量集作为支持向量机(SVM)模型的输入,并利用现场历史数据建立了IPMI-SVM模型,将其与传统SVM方法进行了对比.结果表明:IPMI-SVM模型具有较高的预测精度,IPMI法可有效提高模型的泛化能力和鲁棒性,降低了模型复杂度.
烟气脱硝; 偏互信息; 支持向量机; 变量选择; 数据建模
随着环保要求的不断提高,火电厂SCR脱硝系统的高效运行得到了广泛关注[1-3].准确的SCR脱硝系统模型是优化控制的基础,而输入变量的正确选择是确保模型准确的前提.漏选变量会造成模型不完整,无法正确反映建模对象的特性,降低模型精度;而多选变量会引入冗余信息或噪声信息,导致模型泛化能力减弱,同时也会增加建模耗时.SCR脱硝系统反应机理复杂,变量之间存在强耦合关系,基于机理分析的变量选择方法容易出现多选或漏选现象.随着数据分析方法的不断发展,数据驱动的变量选取方法得到了广泛的关注和应用.Mehmood等[4]详细介绍了目前常用的变量选择方法.王慧文等[5]根据Gram-Schmidt变换原理,提出了一种基于主基底分析的变量选择方法.徐富强等[6]将径向基函数(RBF)神经网络模型与平均影响值(MIV)算法结合,提出了一种变量选择方法,并实例验证了该方法的有效性.Tran等[7]利用模型均方根误差和决定系数对变量进行评价,采用遗传算法进行变量选择.
信息熵是信息量化表达的一种方法,互信息(mutual information, MI)在信息熵的基础上对变量之间的关系进行了度量[8].Battiti[9]利用互信息对神经网络的输入变量进行筛选,并对筛选结果进行了分析.但是由于变量之间普遍存在耦合关系,为了消除耦合对变量选取带来的不利影响,May等[10]提出了偏互信息(partial mutual information, PMI)法.笔者对PMI法进行改进,提出了IPMI (improved partial mutual information)法,采用插值法计算回归值,利用Benchmark验证方法的有效性.将IPMI法应用于SCR脱硝系统中进行变量选取,并将选取结果应用于支持向量机(SVM)数据建模方法中.
1 IPMI变量选取方法
信息熵的提出实现了信息的量化度量.其中,变量间共同含有的信息对应的信息熵称为互信息.互信息的计算公式为
(1)
(2)
式中:I(x,y)为x、y的互信息;xi、yi为第i组样本数据;p(x)、p(y)为概率密度函数;p(x,y)为联合概率密度函数;n为样本个数;h为核函数参数;Σ为x的方差.
对于多输入系统,由于输入变量间存在耦合关系,在变量选取的过程中需要计算已选变量的回归值,根据回归值剔除已选变量的信息并计算PMI值.将PMI值作为变量选取的依据可以避免耦合信息对选取准确性的不利影响[11-12].回归值通常利用条件期望来计算,但由于变量的概率密度是根据核密度估计(KDE)计算的,概率密度的计算误差在条件期望的计算过程中进一步扩大,从而严重影响选取结果的准确性[13-14].为了提高变量选取的准确性,利用插值法计算回归值,计算式如下:
(3)
(4)
式中:my(x)为回归值;f(x)为x、y之间的回归函数;C为常数;R为余项.
通常,R值较小可以忽略不计,而且PMI法以马氏距离作为计算依据,常数C对计算结果没有影响,因此也不必进行估算.f′(x)可以通过泰勒级数求得:
(5)
(6)
式中:x1、x2、y1、y2分别为输入、输出变量的观测值;R1和R2包括了其他输入变量对应的输出值以及拉格朗日余项.
通过式(5)和式(6)可得:
(7)
利用n个观测值对f′(x1)进行估计:
(8)
为减少R对f′(x1)计算精度的影响,要尽可能增大n的取值,同时应利用距离x1较远的观测值进行计算.
设输入变量集为X,输出变量为Y,已选变量集为S,最大PMI值对应的候选变量为XS,IPMI法的变量选取流程如下:(1)初始化S,设为空集;(2)当X≠∅时;(3)计算u=Y-my(S),my(S)利用插值法求取;(4)对于每一个输入变量,分别计算I(Xj,u),并选取I(Xj,u)最大值对应的Xj作为XS;(5)计算赤池信息量准则(AIC)值,若AIC值减小,将XS移入S,返回第(2)步,若AIC值不减小则终止筛选.
由于回归值计算忽略了常数C,所以AIC值的计算也进行了相应改变,具体公式为
(9)
式中:hAIC为AIC值;ui为根据已选变量计算的Y的回归残差;d为变量集S的维数.
随着变量选取过程的进行,AIC值不断减小,当AIC值达到最小时最优自变量集合提取完毕.
2 Benchmark仿真验证
利用3组Benchmark数据集验证IPMI法的有效性并与传统PMI法进行比较.这些数据集具有多重共线性、非线性和强噪声干扰等特点,被广泛应用于变量选取方法的验证[8,10].数据集模型如下:
(1)线性自回归时序模型.
AR4xt=0.6xt-1-0.4xt-4+0.1ε
(10)
(2)非线性阈值自回归时序模型.
(11)
(3)非线性输入输出函数.
(12)
式中:x~N(0,1)为备选输入变量;ε~N(0,1)为噪声干扰.
对于前2组数据集,输出变量为xt,输入变量集为xt-i(i=1,2,…,10)和5组白噪声,共15个.对于Mexican Hat数据集,输出变量为y,输入变量为x1、x2和13组白噪声,共15个.3组Benchmark数据集的样本量设置为100和300,分别利用PMI法和IPMI法进行变量选取,每种情况进行了50次仿真.当且仅当选取结果与实际输入完全一致时视为选取正确,其他如多选或漏选都视为错选.仿真结果如表1所示.
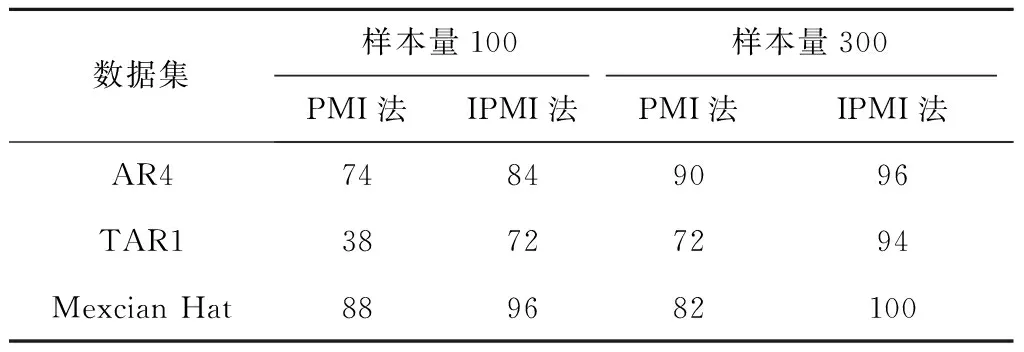
表1 Benchmark验证结果正确率
从表1可以看出,与PMI法相比,IPMI法筛选的正确率更高,说明插值法计算回归值更准确.随着样本量的增加,IPMI法的正确率也随之升高.因为在求取一阶导数的过程中,计算误差随着样本量的增加而减小,有利于提高筛选的正确率.同时,对比线性和非线性自回归数据集可以发现,前者的正确率更高,因为当输入变量相互耦合时,线性系统的插值余项为零,回归值计算更准确.通过仿真验证可以发现,当样本量足够多时,IPMI法的筛选正确率在94%以上,可以满足实际应用的要求.
3 IPMI法的应用
3.1SCR脱硝反应分析
随着污染物排放标准要求日益严格,SCR脱硝系统在火电厂中得到了广泛的应用.某1 000 MW超超临界机组燃煤锅炉的SCR烟气脱硝装置如图1所示.该SCR脱硝系统采用TiO2作为催化剂,稀释空气与氨气在混合器充分混合,经喷氨控制阀调整流量后通过喷嘴喷出,并与来自省煤器的烟气充分混合.混合气体在催化剂的作用下发生选择性催化还原反应,烟气中的NOx与NH3发生反应,生成无害的氮气和水,从而实现烟气脱硝[15].
用两倍稀释法将铁皮石斛匀浆液稀释成质量分数分别为1.25%、2.5%、5%、10%和20%的系列溶液。向制备好的培养基中分别加入不同浓度的稀释液1 mL,涂布均匀后置于培养箱中20 min。取出后,再分别加200 uL菌液于培养基表面,涂布均匀,倒置于培养箱中,37℃培养24 h。每个浓度重复3次,以不长菌的最低浓度作为最小抑菌浓度。
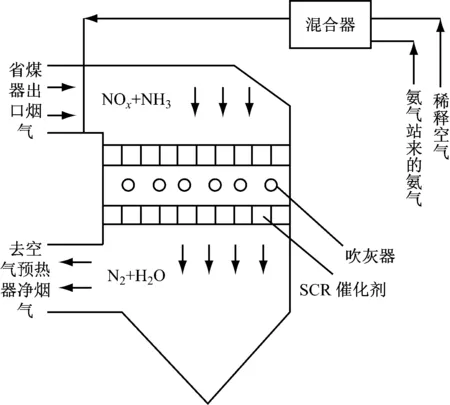
图1 SCR烟气脱硝装置结构图Fig.1 Structure of the SCR denitrification system
SCR脱硝过程中发生的化学反应主要有:
4NH3+4NO+O2=4N2+6H2O
(13)
4NH3+3O2=2N2+6H2O
(14)
其中,脱硝效率受到氨氮比、烟气含氧体积分数、反应温度和反应时间等因素的影响.当氨氮比小于1时,脱硝效率随着喷氨量的增加而升高;当氨氮比大于1时,脱硝效率较高,但过量喷氨会导致氨逃逸率升高.烟气含氧体积分数也会影响脱硝效率,烟气含氧体积分数过高会增加氨气的氧化反应,从而降低脱硝效率;烟气含氧体积分数过低会造成NOx催化还原反应不充分,导致脱硝效率降低.SCR脱硝系统的NOx催化还原反应温度为300~400 ℃,在此区间内脱硝效率随反应温度的升高而升高.此外,反应时间也是影响脱硝效率的重要因素,反应时间越长,反应越充分,脱硝效率越高.
根据以上分析,选取喷氨量、氨逃逸量、SCR入口NOx质量浓度(简称入口NOx质量浓度)、入口烟气含氧体积分数、出口烟气含氧体积分数、入口烟温、烟气流量、SCR脱硝系统出入口压差和机组负荷等9个变量作为输入变量.由于这9个输入变量相互耦合,所反映的影响因素也相互重叠,因此有必要进行变量筛选,选取最优变量集作为模型输入变量.
3.2数据预处理及变量选择
以某1 000 MW超超临界机组燃煤锅炉SCR脱硝系统为研究对象,选取稳态工况下的历史数据作为样本,根据3σ准则剔除其中的异常值,最终选取400组数据作为训练样本,70组数据作为预测样本.稳态工况判断公式为
(15)
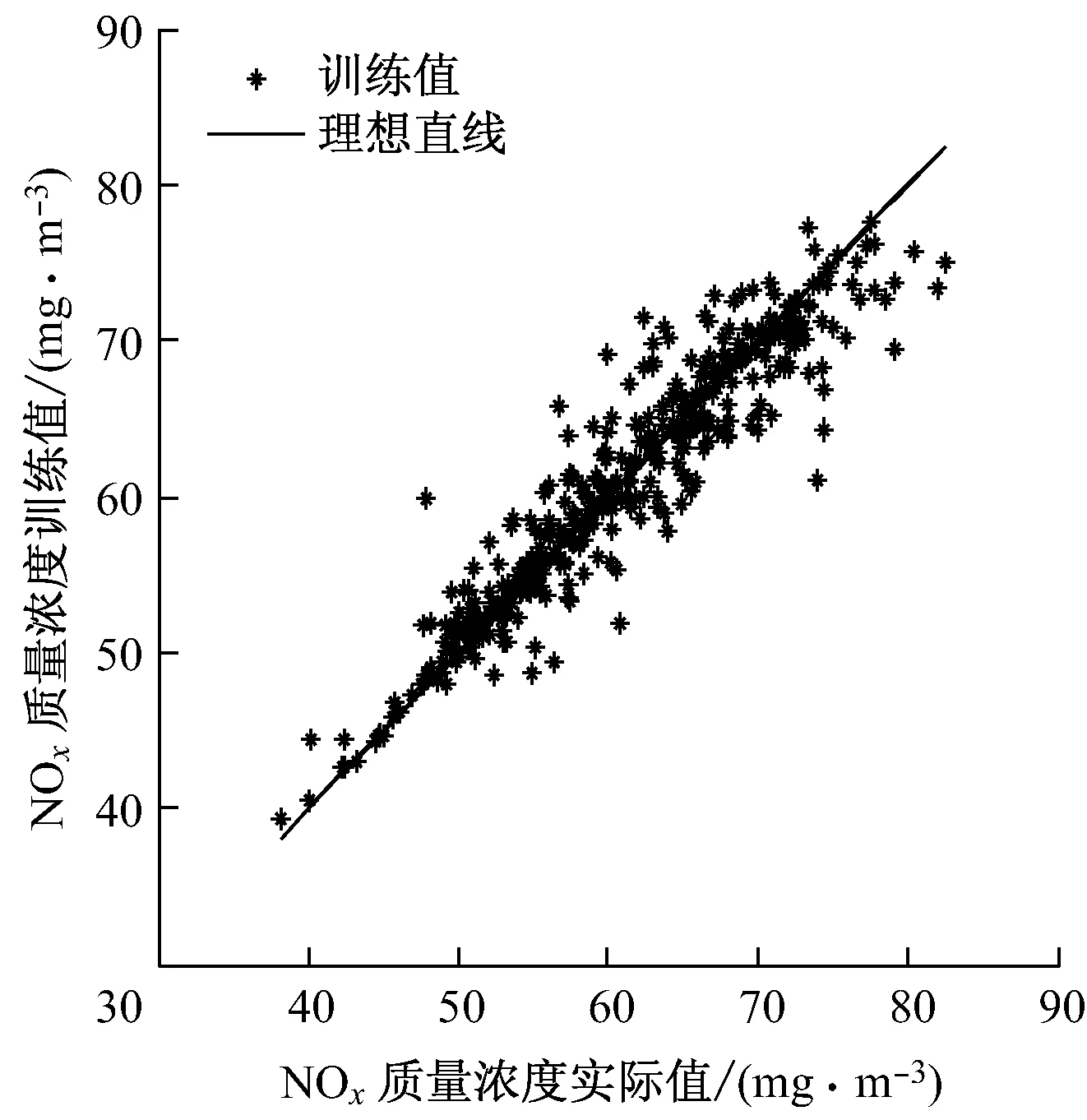
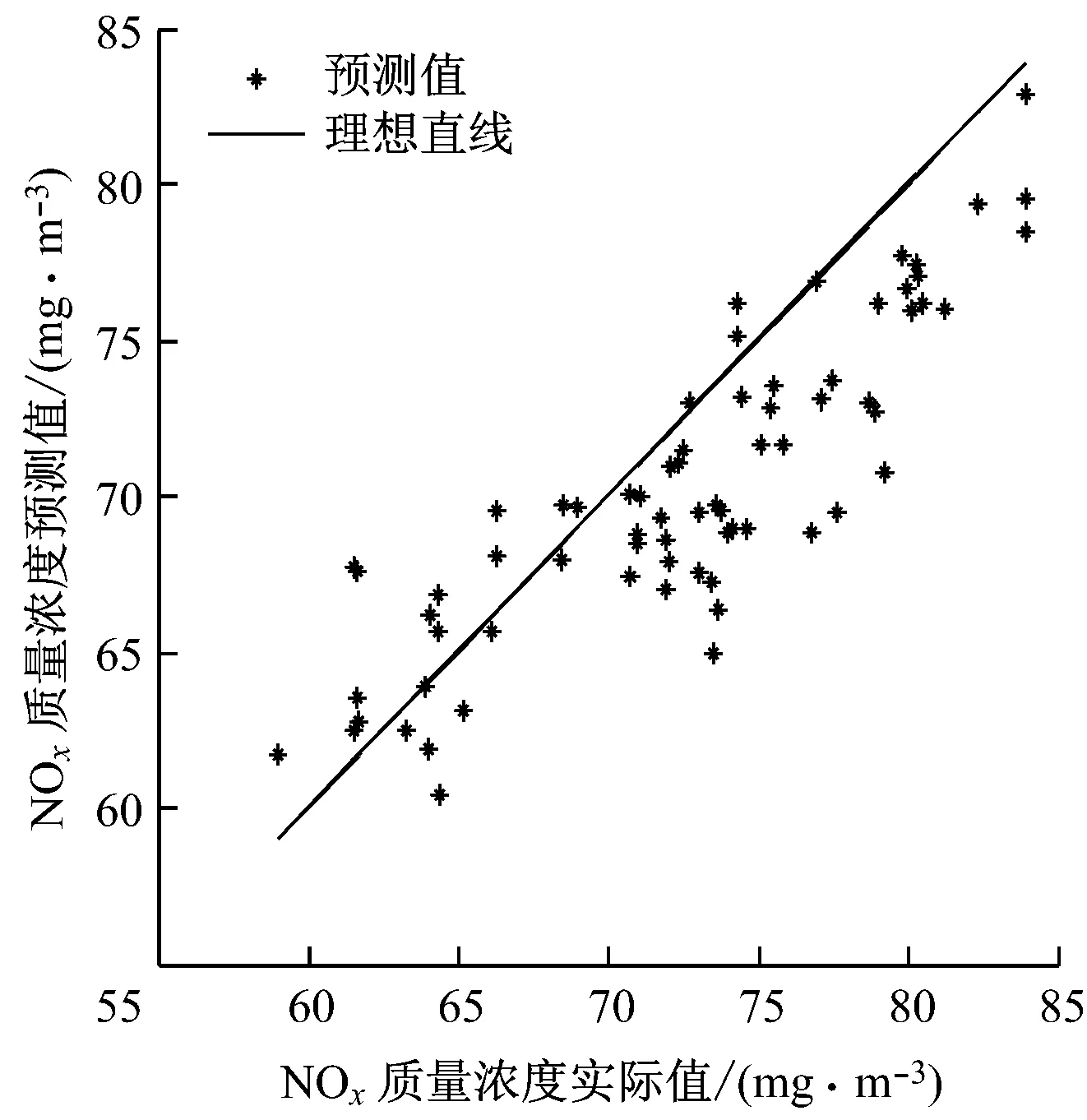
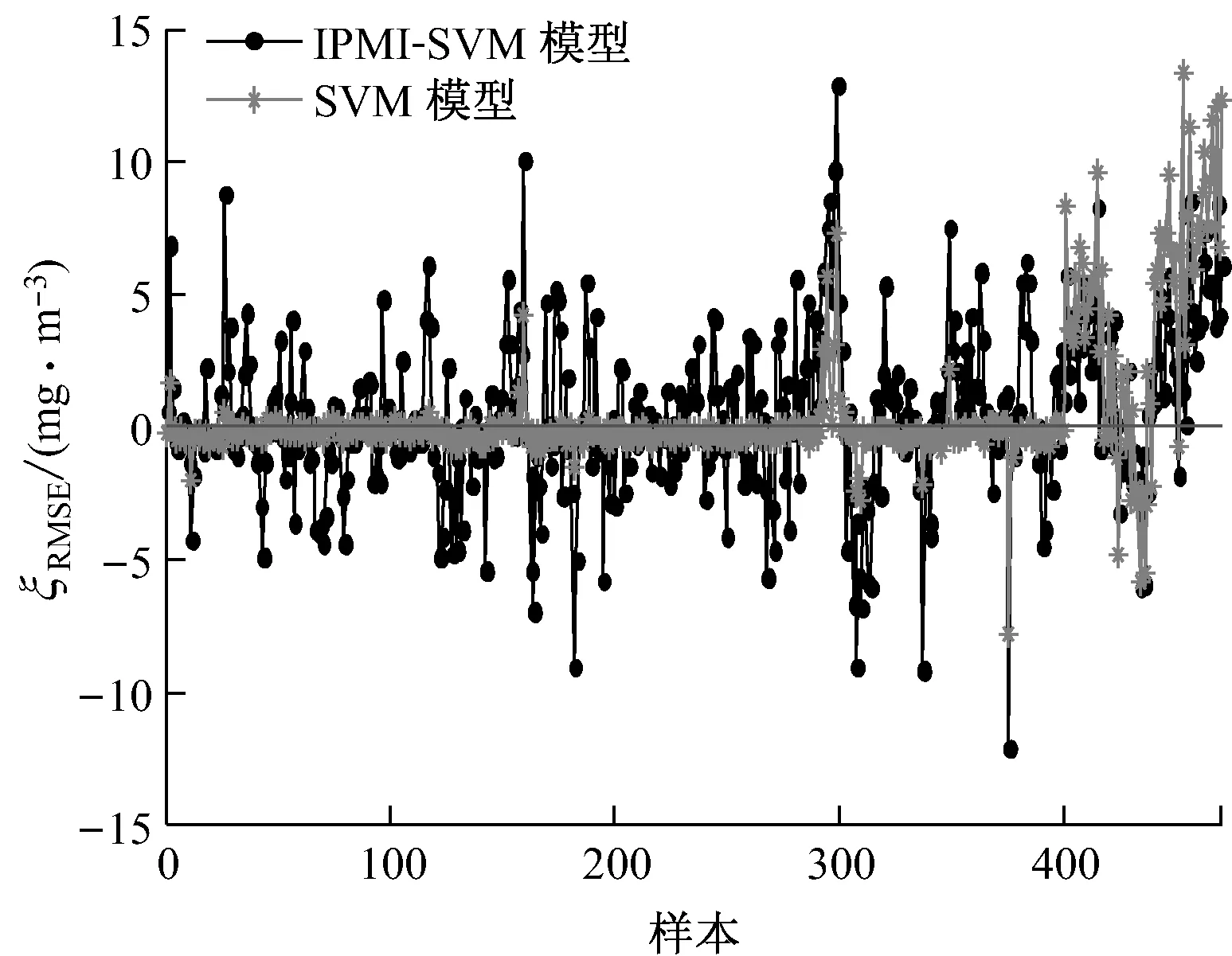
选取一段机组稳定运行时的负荷数据,计算其稳态指标Hmax作为上限值,选取满足H 选取上文9个变量作为备选输入变量,SCR出口NOx质量浓度(简称出口NOx质量浓度)作为输出变量.采用IPMI法进行变量选取,选取过程如图2所示.从图2可以看出,AIC值持续减小直至第5个变量被选取出来,AIC值最小为-1 765.9.选取的5个输入变量为入口NOx质量浓度、喷氨量、出口烟气含氧体积分数、入口烟温和机组负荷. 上述5个变量的数据分布如图3所示.其中,机组负荷的分布范围为700~800 MW,包括785 MW、755 MW和705 MW 3组稳态工况.与机组负荷相对应,喷氨量和入口NOx质量浓度也分为3组稳态工况.其中,喷氨量的分布范围为42~184 kg/h,入口NOx质量浓度的分布范围为149~405 mg/m3,入口烟温分布范围为343~355 ℃,出口烟气含氧体积分数分布范围为5.8%~7.4%. 图2 IPMI法变量选取过程Fig.2 Selection of IPMI variables 图3 变量数据分布图Fig.3 Data distribution of different variables 3.3模型建立及结果分析 SVM方法是一种数据驱动建模方法,在工业过程建模中已取得广泛应用[17-19].Lü等[20]利用SVM方法建立了锅炉燃烧NOx排放模型.利用全部输入变量建立SVM模型会将不必要的冗余信息或噪声信息引入模型,导致模型预测精度下降,造成过拟合.同时,输入变量过多也会产生模型参数辨识困难、模型复杂度高等问题.当模型输入变量不足时,输入变量无法充分反映建模对象的特性,会对模型的学习和泛化能力造成不利影响.针对以上问题,将IPMI法与SVM法结合,利用IPMI法对输入变量进行筛选,然后利用最优变量集建立SVM模型,在保证模型准确性的同时避免了过拟合,提高了模型的泛化能力. 将入口NOx质量浓度、喷氨量、出口烟气含氧体积分数、入口烟温和机组负荷5个变量作为模型输入,出口NOx质量浓度作为模型输出,利用训练样本建立SCR脱硝系统的SVM模型,并利用预测样本对模型进行验证.模型精度评价指标采用均方根误差ζRMSE和平均绝对百分比误差ζMAPE,计算公式如下: (16) (17) IPMI-SVM模型的训练及预测效果如图4和图5所示.从图4和图5可以看出,出口NOx质量浓度训练值和预测值分布在理想直线附近,训练精度评价指标为ζRMSE,T=2.855 6 mg/m3和ζMAPE,T=3.14%,预测精度评价指标为ζRMSE,P=3.933 7 mg/m3和ζMAPE,P=4.49%,下标T和P分别代表训练和预测精度评价指标.训练和预测效果表明,IPMI-SVM模型具有较强的学习和泛化能力,反映了SCR脱硝系统输入、输出变量间的非线性关系. 为了验证IPMI法对模型准确性的改善作用,选取全部9个输入变量建立SCR脱硝系统的SVM模型作为对比.模型输出为出口NOx质量浓度,训练样本和预测样本与IPMI-SVM模型一致,对比结果如表2所示.模型误差对比图见图6. 图4 IPMI-SVM模型训练效果Fig.4 IPMI-SVM training effect 图5 IPMI-SVM模型预测效果Fig.5 IPMI-SVM prediction effect 表2 不同模型的对比 从表2可以看出,SVM模型的ζMAPE,T=0.75%,ζMAPE,P=7.12%,训练误差很小但是预测误差很大,模型出现了过拟合现象.相比之下,IPMI-SVM模型的ζMAPE,T=3.14%,ζMAPE,P=4.49%,预测精度有所提高,说明IPMI法的引入有效降低了模型的预测误差,增强了模型的泛化能力,避免了过拟合现象的产生.此外,IPMI-SVM模型的建模耗时更短,因为最优变量集的选取减少了模型参数,降低了模型复杂度. 图6 不同模型的ξRMSE对比Fig.6 Comparison of model errors 从图6可以看出,IPMI-SVM模型的训练误差略高于SVM模型.这是因为SVM模型利用全部输入变量作为模型输入,在模型建立的过程中将冗余信息和噪声信息也引入模型中,虽然SVM模型具有很高的训练精度,但是模型泛化能力有限,容易产生过拟合现象.IPMI-SVM模型在最优变量集的选取过程中剔除了冗余信息或噪声信息,模型中不包含噪声模型,但是样本中却包含噪声数据,模型无法反映这部分噪声的数据特性,从而导致训练误差增大.通过2种模型的对比可以发现,IPMI法有效避免了冗余信息和噪声信息对模型准确性的不利影响,在保证模型学习能力的同时增强了模型的泛化能力和鲁棒性. 准确的模型是SCR脱硝系统优化控制的基础,而最优变量集的选取是确保模型准确性的前提.由于利用条件期望计算回归值会对筛选正确率产生不利影响,对传统PMI法进行了改进,采用插值法计算回归值,并用Benchmark验证了方法的有效性.仿真结果表明,IPMI法的筛选正确率高于PMI法,可以满足实际应用的要求.将IPMI法与SVM方法结合,应用于火电厂SCR脱硝系统建模,利用现场历史数据建立了IPMI-SVM模型,并与传统SVM模型进行比较.结果表明,IPMI-SVM模型具有较强的学习和泛化能力,IPMI法在提高模型准确性的同时降低了模型复杂度. [1]凌忠钱,曾宪阳, 胡善涛,等.电站锅炉SCR烟气脱硝系统优化数值模拟[J]. 动力工程学报, 2014,34(1):50-56. LING Zhongqian, ZENG Xianyang, HU Shantao,etal. Numerical simulation on optimization of SCR denitrification system for coal-fired boilers[J]. Journal of Chinese Society of Power Engineering, 2014, 34(1):50-56. [2]朱天宇,李德波,方庆艳,等.燃煤锅炉SCR烟气脱硝系统流场优化的数值模拟[J].动力工程学报,2015,35(6):481-488. ZHU Tianyu, LI Debo, FANG Qingyan,etal. Flow field optimization for SCR system of coal-fired power plants [J]. Journal of Chinese Society of Power Engineering, 2015,35(6):481-488. [3]杨建国,胡劲逸,赵虹,等. 660 MW超超临界机组运行方式对SCR系统氨逃逸率的影响[J].动力工程学报, 2015,35(6):476-480. YANG Jianguo, HU Jinyi, ZHAO Hong,etal. Effects of boiler control mode on ammonia escape of the SCR system in a 660 MW ultra-supercritical unit [J]. Journal of Chinese Society of Power Engineering, 2015,35(6):476-480. [4]MEHMOOD T, LILAND K H, SNIPEN L,etal. A review of variable selection methods in Partial Least Squares Regression[J]. Chemometrics & Intelligent Laboratory Systems, 2012, 118(16):62-69. [5]王惠文,仪彬,叶明.基于主基底分析的变量筛选[J].北京航空航天大学学报, 2008, 34(11):1288-1291. WANG Huiwen, YI Bin, YE Ming. Variable selection based on principal basis analysis [J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(11):1288-1291. [6]徐富强,刘相国.基于优化的RBF神经网络的变量筛选方法[J].计算机系统应用, 2012, 21(3):206-208. XU Fuqiang, LIU Xiangguo.Variables screening methods based on the optimization of RBF neural network [J]. Computer Systems & Applications, 2012, 21(3):206-208. [7]TRAN H D, MUTTIL N, PERERA B J C. Selection of significant input variables for time series forecasting[J]. Environmental Modelling & Software, 2015, 64(64):156-163. [8]SHARMA A. Seasonal to interannual rainfall probabilistic forecasts for improved water supply management: part 1—a strategy for system predictor identification[J]. Journal of Hydrology, 2000, 239(1/2/3/4): 232-239. [9]BATTITI R. Using mutual information for selecting features in supervised neural net learning[J]. IEEE Transactions on Neural Networks, 1994, 5(4):537-550. [10]MAY R J, MAIER H R, DANDY G C,etal. Non-linear variable selection for artificial neural networks using partial mutual information[J]. Environmental Modelling & Software, 2008, 23:1312-1326. [11]LI X, ZECCHIN A C, MAIER H R. Improving partial mutual information-based input variable selection by consideration of boundary issues associated with bandwidth estimation[J]. Environmental Modelling & Software, 2015, 71:78-96. [13]SILVERMAN B W. Density estimation for statistics and data analysis[M]. New York, USA: Chapman & Hall,1986. [14]SCOTT D W. Multivariate density estimation: theory, practice, and visualization[M]. New York,USA:John Wiley & Sons,2015. [15]周洪煜,张振华,张军,等. 超临界锅炉烟气脱硝喷氨量混结构-径向基函数神经网络最优控制[J].中国电机工程学报, 2011,31(5):108-113. ZHOU Hongyu, ZHANG Zhenhua, ZHANG Jun,etal. Mixed structure-radial basis function neural network optimal control on spraying ammonia flow for supercritical boiler flue gas denitrification [J]. Proceedings of the CSEE, 2011, 31(5):108-113. [16]吕游,刘吉臻,赵文杰,等.基于分段曲线拟合的稳态检测方法[J].仪器仪表学报,2012,33(1): 194-200. LÜ You, LIU Jizhen, ZHAO Wenjie,etal. A steady-state detecting method based on piecewise curve fitting[J]. Chinese Journal of Scientific Instrument, 2012,33(1): 194-200. [17]谷丽景,李永华,李路.电站锅炉燃烧优化混合模型预测[J].中国电机工程学报,2015,35(9): 2231-2237. GU LiJing, LI Yonghua, LI Lu. Hybrid model prediction of utility boiler combustion optimization [J]. Proceedings of the CSEE, 2015, 35(9): 2231-2237. [18]李新利,李玲,卢钢,等.基于火焰自由基成像和支持向量机的燃烧过程NOx排放预测[J].中国电机工程学报, 2015,35(6): 1413-1419. LI Xinli, LI Ling, LU Gang,etal. NOxemission prediction based on flame radical profiling and support vector machine [J].Proceedings of the CSEE, 2015, 35(6): 1413-1419. [19]IZADYAR N, GHADAMIAN H, ONG H C,etal. Appraisal of the support vector machine to forecast residential heating demand for the District Heating System based on the monthly overall natural gas consumption[J]. Energy, 2015, 93(9): 1558-1567. [20]LÜ You, LIU Jizhen, YANG Tingting. Nonlinear PLS integrated with error-based LSSVM and its application to NOxmodeling [J]. Industrial & Engineering Chemistry Research, 2012, 51(49): 16092-16100. Modeling of Power Plant SCR Denitrification System Based on Improved Partial Mutual Information Method QINTianmu1,LIUJizhen1,FANGLianhang2,LIUHongyan2,YANGTingting1,LÜYou1 (1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China;2. Hainan Electric Power Technology Research Institute, Haikou 570203, China) To solve the problem of large error in calculating the regression value with conditional expectation by traditional partial mutual information (PMI) method that may produce negative effect on the selection accuracy, an improved partial mutual information (IPMI) algorithm was proposed to calculate the regression value using interpolation method, of which the effectiveness was validated by Benchmark software. The IPMI algorithm was then applied to the SCR denitrification system of a power plant. The specific way is to set up an IPMI-SVM model based on the historical data by taking the optimal variable set of IPMI as the input of support vector machine (SVM) model, and then to compare the IPMI-SVM model with traditional SVM method. Results show the IPMI-SVM model has relatively high prediction accuracy, while the IPMI method can effectively improve the generalization ability and robustness of the model and reduce the model complexity. flue gas denitrification; partial mutual information; support vector machine; variable selection; data modeling 2015-10-13 2016-01-05 中央高校基本科研业务费专项资金资助项目(2015XS69,2016MS47);中国南方电网公司科技资助项目(073000KK51140001) 秦天牧(1990-),男,北京人,博士研究生,研究方向为火电厂SCR烟气脱硝系统建模与优化控制.电话(Tel.):13466504095;E-mail:qintianmu@ncepu.edu.cn. 1674-7607(2016)09-0726-06 TK39 A学科分类号:470.20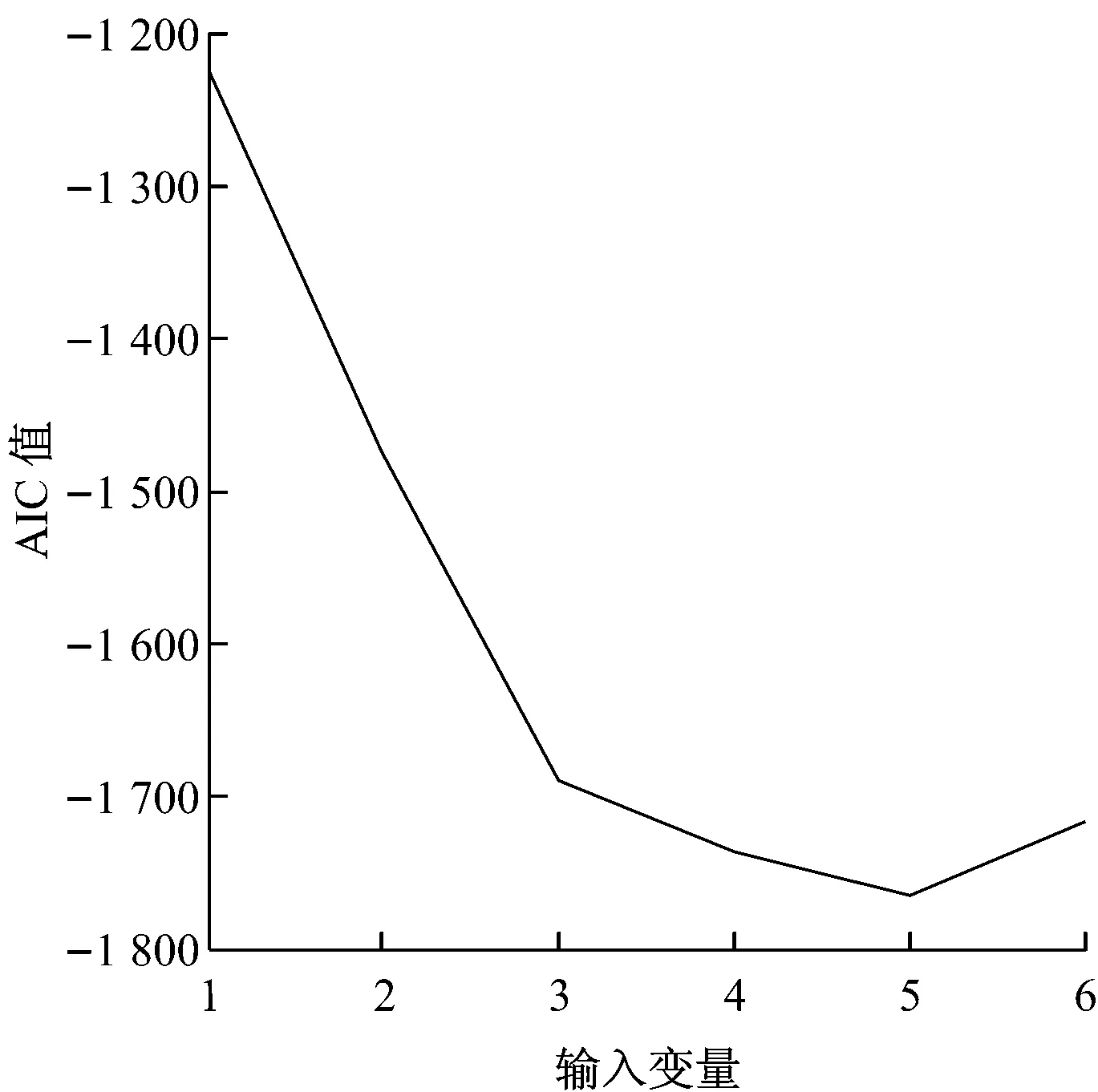
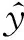
4 结 论

