材料沉降对水平圆形管道保温层设计的影响

赵　旭，　沈　惬，　张　宁，　孙大明，　邹　江

(浙江大学 能源工程学院， 杭州 310027)



材料沉降对水平圆形管道保温层设计的影响

赵旭，沈惬，张宁，孙大明，邹江

(浙江大学 能源工程学院， 杭州 310027)

定量分析了保温层材料下沉对经济厚度计算的影响，并通过分析整个保温层传热的热通路提出了经济厚度法的修正方法.在理论上研究经济厚度法的设计思路，通过修改设计参数值研究不同设计参数对经济厚度的影响.利用修正后的经济厚度法对黄台电厂实际运行的热力管道保温层进行设计.结果表明:采用修正后的经济厚度法可以使年总费用节约0.7%左右；热力管道直径D0、下沉率M和管内介质温度T0是影响经济厚度设计的主要参数.

火电厂； 热力管道； 散热； 保温； 经济厚度法

符号说明：

D0——热力管道直径，m

D1——保温层外表面直径，m

qL——周向漏热量，W

qf——下沉后的周向漏热量，W

T0——管内介质温度，℃

Tw——保温层外表面温度，℃

Ts——环境温度，℃

h——对流传热系数，kg/(m2·K)

Pi——保温层造价，元/m3

Pp——保护层造价，元/m2

M——下沉率

λ——导热系数，kg/(m·K)

τ——年运行时间，h

S——初始投资年分摊利率

Lf——下沉深度，m

D1f——考虑下沉之后的保温层外径，m

Pef——考虑下沉之后的散热导致的可用能损失，元

Pf——考虑下沉之后的年总费用，元

δ——传统设计保温层厚度，m

δf——考虑下沉之后的设计保温层厚度，m

Δδ——修正前后经济厚度差值，m

Pe——热价，元/GJ

火力发电厂中通过管道输送高温蒸汽、烟气、预热空气等载热介质，而在这些管道外部需要包裹保温层以保障生产安全，提高发电效率.当今世界能源消耗的30%～40%都用于工业生产领域，热力管道的保温对于节能减排具有重要意义[1].

目前，国内外学者主要通过经济厚度法对热力管道的保温层进行设计，该方法在设计过程中同时考虑了保温层铺设时的投资年分摊费用和投入使用后的年散热损失费用，取二者之和最小时的保温层厚度，即为“经济厚度”[2].我国目前已经出台了一系列相关章程，规定了采用经济厚度法设计热力管道保温层的流程[3-4].

经济厚度法在热力管道保温层设计方面发挥了很大的作用.Basogul等[5]的研究表明采用经济厚度法进行保温层设计可以使火力发电厂的CO2排放量减少21%左右；Sahin等[6]指出在进行经济厚度的设计过程中，管外自然对流和辐射的影响不可忽视；也有研究发现在进行经济厚度的设计时，引入分析的方法可以使经济性得到进一步提升[7].

依据规范，在采用经济厚度法进行设计时，通常认为管道周向的保温层是均匀厚度分布的，并在此假设的基础上计算热力管道的周向漏热量.近来，已有研究发现受管道运输过程中漏热的影响，管内介质的温度发生变化，从而导致管道不同部位的经济厚度发生变化[8].也有研究显示管道外部空气对流采用定传热系数和变传热系数会导致经济厚度法的设计结果不同[9].笔者所在课题组在研究热力管道保温层时发现，由于重力等因素的影响，水平圆形管道的保温材料常常会发生下沉现象，使管道周向包裹厚度不均，进而导致管道实际漏热量大于设计值，影响了保温设计的经济性.笔者利用形状因子法定量讨论了由于保温材料下沉导致的周向漏热不均对热力管道保温性能的影响，并提出了修正方法，对于完善经济厚度法，提高热力管道保温的经济性具有一定的指导意义.

1　经济厚度法改进的理论基础

1.1经济厚度法原理

图1为经济厚度法的原理示意图.图中曲线A为初始投资年分摊费用随保温层厚度的变化曲线，曲线B为年散热费用，曲线C为二者之和，即年平均总费用.随着保温层厚度的增加，初始投资的年分摊费用增加，而年散热费用减少，年平均总费用先减少后增加.年平均总费用最低时对应的保温层厚度即为“经济厚度”，其计算公式为

(1)

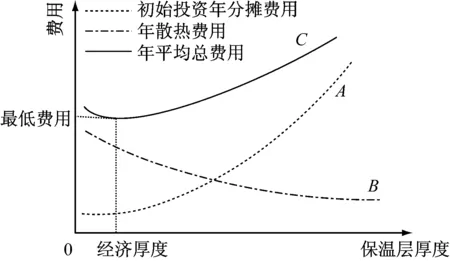
图1　经济厚度法原理示意图Fig.1　Design principles of the economic thickness method

1.2周向导热量的改进计算

图2为水平圆形单层保温管道截面示意图，左边为传统设计的热力管道保温层，右边为下沉后的热力管道保温层，在传统设计中各个角度保温层厚度是均匀的，管道和保温层的内部和外表面为等温面，则保温层导热量的计算公式为

(2)

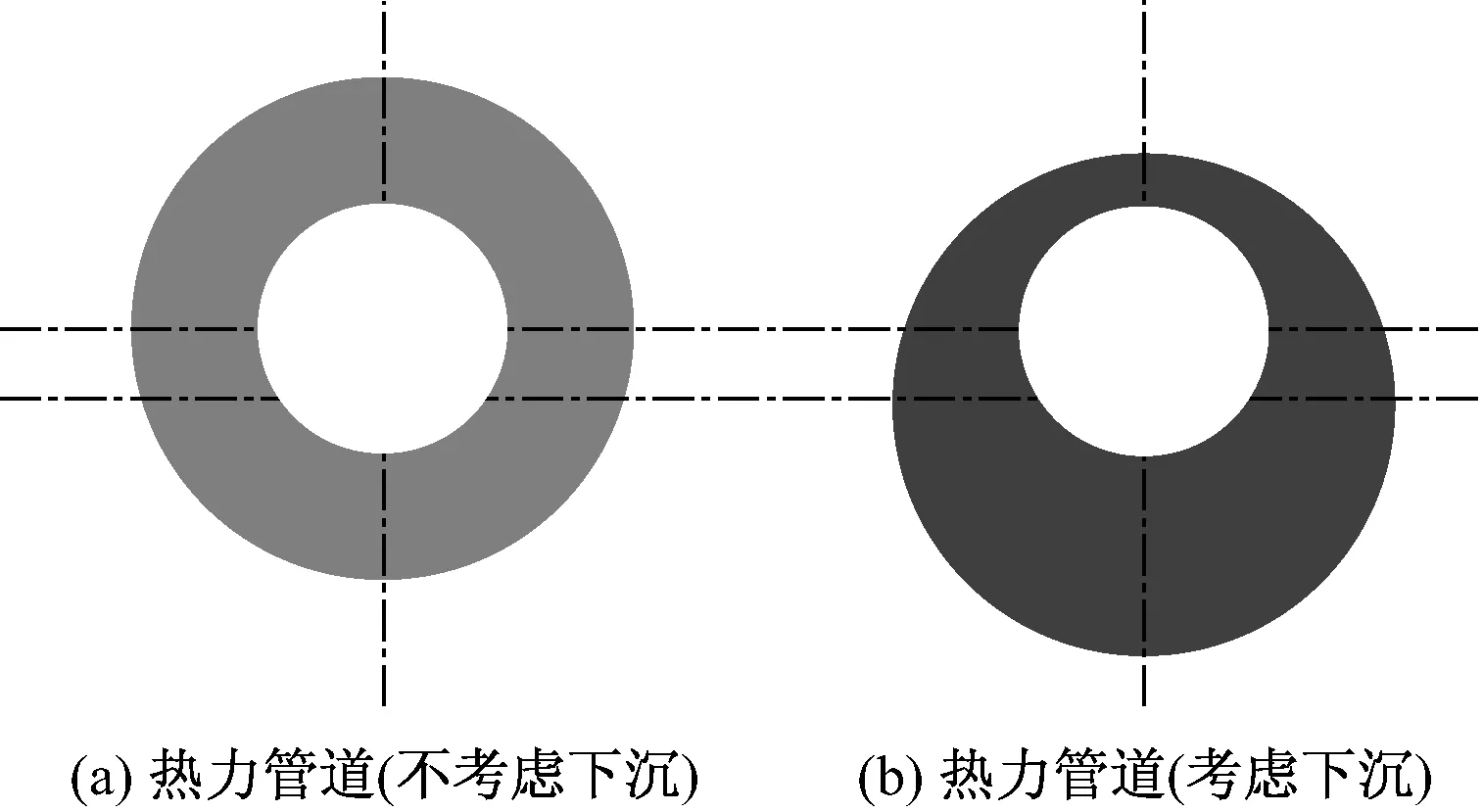
图2　水平单层保温圆管示意图Fig.2　Single-layer insulation for horizontal circular heating pipeline

然而在保温管道的实际运行过程中，由于重力等因素的影响，管道保温层会发生下沉，导致各个角度保温层厚度发生变化，如图2(b)所示.此时按照式(2)计算漏热量会导致很大的误差.

对于图2(b)形状的热力管道截面的导热问题，可以按照形状因子法计算导热量.该计算基于以下假设：(1) 保温材料下沉后的保温层仍然呈圆形；(2) 忽略由于保温材料形状变化导致的管外对流传热系数的变化；(3) 保温材料下沉后，保温层外表面为等温面；(4) 忽略由于保温层厚度变化导致的管外对流传热系数的变化，即修正前后经济厚度计算使用相同保温层对流传热系数.

图3中A点为保温层圆心，B点为热力管道圆心，由于保温材料下沉，A点与B点不重合，保温层厚度δ会随着θ角度发生变化.

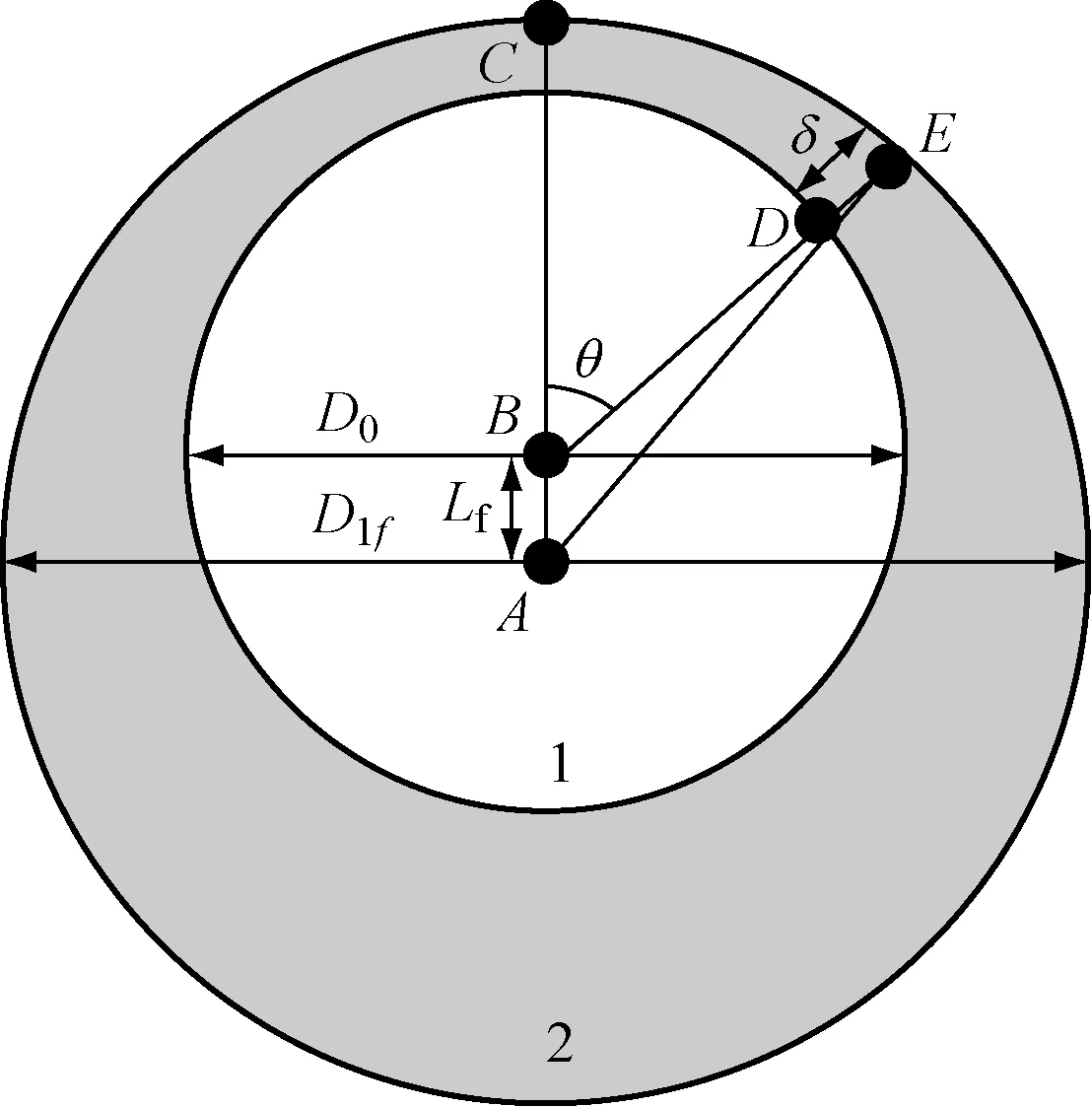
图3　保温层下沉示意图Fig.3　Sinking diagram of the insulation material

对于下沉深度为Lf的热力管道，其导热量为

(3)

式(3)中K为管道偏心保温层的形状因子[10]，当管道长度远远大于外表面直径时，单位长度该种管道的形状因子为

(4)

传统设计方法所用计算公式即是Lf=0时形状因子法的计算公式，由于导热量变化会影响经济厚度的设计，考虑保温材料下沉后保温层外径变为D1f，其计算方法将在下一节介绍.

1.3经济厚度的改进计算

根据形状因子法对管道导热量进行修正后，由于设计的导热量发生了变化，经济厚度值必然会相应发生变化.因此，整个经济厚度法的设计步骤也需

要进行修正.

由于保温材料下沉，热力管道保温层厚度发生变化，会导致保温层外表面局部温度和局部漏热量不均匀，对于本文讨论的管内介质为300 ℃，环境温度为25 ℃的热力管道，外表面最高局部温度和最低局部温度之间相差15 K左右，此时若假设管道外表面是一个温度为外表面平均温度的等温面，总漏热量和实际漏热量相差0.08%左右，因此可以按照外表面为等温面进行设计计算，也证明了1.2节中假设(3)的合理性.

对保温层厚度进行修正后，管外空气对流传热系数也会发生变化，从而影响漏热量的计算.然而由于管外对流热阻只占整个传热总热阻的5%左右，经济厚度变化导致对流传热系数的变化在2%左右，由此产生的总漏热量变化在0.1%以内，对经济厚度的影响可以忽略不计，证明了1.2节中假设(4)的合理性.

考虑保温材料下沉之后，散热导致可用能损失总费用为

(5)

式(5)中qf由式(3)和式(4)计算得到，质系数Ae用于计算可用能损失在总散热量中所占的比例，年运行时间τ和热价Pe均可根据相关章程进行计算[4].式(4)中的下沉深度Lf受到保温层厚度、热力管道直径等诸多因素的影响，为了方便计算，可以通过保温层外表面直径D1f将下沉深度Lf转化为无量纲的下沉率M.

(6)

则修正之后的热力管道运行总费用为

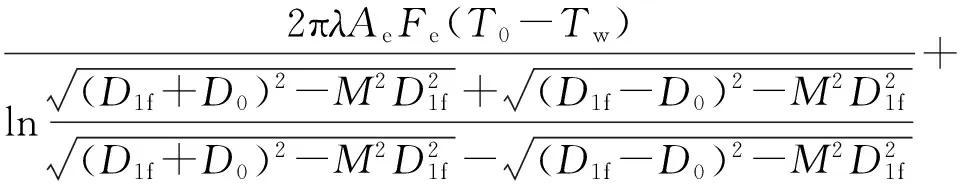
(7)

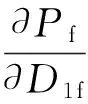
(8)

其中，

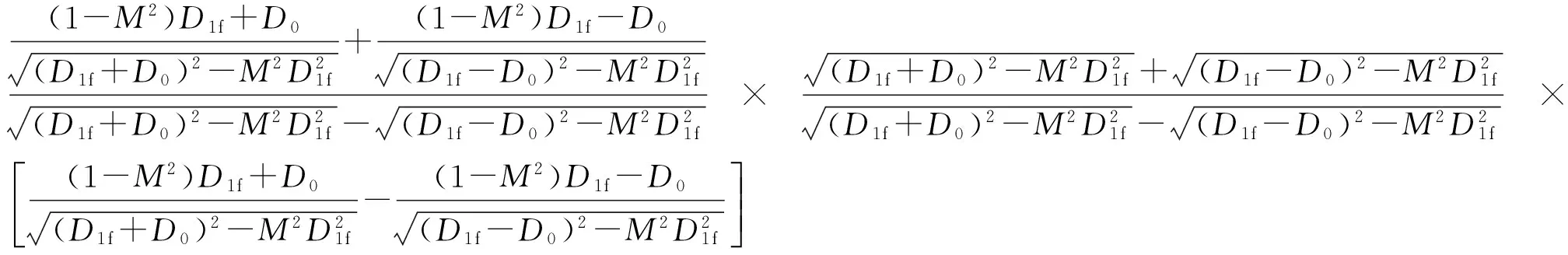
根据式(8)即可得到保温层外表面直径D1f，则修正之后的平均经济厚度δf为

(9)

2　影响经济厚度法修正计算的因素及其规律

2.1经济厚度法修正实例

为了验证和显示经济厚度法修正的必要性和效果，选取济南市黄台电厂9号机组的低温蒸汽管道进行修正计算.该管道的照片如图4所示，管道直径为0.5 m，外部采用复合硅酸盐(毡)包裹进行单层保温，全部保温层设计参数见表1.

图4　低温蒸汽管道Fig.4　Low-temperature steam pipeline表1　低温蒸汽管道设计参数Tab.1　Design parameters of the low-temperature steam pipeline

设计参数数值设计参数数值管道直径D0/m0.5管内介质温度/℃300热价Pe/(元·GJ-1)50环境温度/℃25年运行时间/h3000保温层造价/(元·m-3)500质系数1.0保护层造价/(元·m-2)600初始投资年分摊利率0.1保温材料岩棉(毡)下沉率0.2

根据相关设计规程，对于笔者设计的管道，考虑辐射和对流之后管外空气的等效对流传热系数可取5.51 W/(m2·K)，岩棉(毡)的导热系数可按λ=0.049+0.000 18×(Tm-70)进行计算[4].其中，Tm为保温层平均温度，其计算公式为

(10)

经过计算，传统设计方法的保温层经济厚度δ为0.166 2 m.根据式(8)可计算得到修正后的平均保温层经济厚度δf为0.185 m，修正后的平均经济厚度比原经济厚度厚11.3%，这是因为保温材料的下沉导致相同厚度下其保温效果更差，因此在经济厚度法的原理之下，需要周向均匀加厚保温层厚度以保证保温效果，而进行修正计算后，热力管道的实际漏热费用会明显下降.根据式(7)可知，考虑下沉之后设计所得经济厚度下年总运行费用比原设计经济厚度下年运行总费用节约0.7%左右.

2.2各参数对修正前后经济厚度差值的影响

由式(8)可知，保温层的经济厚度由多种因素决定，这些因素中除了年运行时间和质系数根据管道类型直接选取外，其他设计参数常会在一定范围内变化，本节针对图4所示的热力管道，通过单独改变设计计算中的各个参量，计算修正前后的保温层经济厚度差值Δδ的变化，其计算公式为

(11)

2.2.1管道几何参数和热学参数的影响

热力管道的几何参数和热学参数是设计保温层经济厚度的重要参数，也会对修正前后的经济厚度差值Δδ产生影响，其中热力管道直径D0、下沉率M和管内介质温度T0是影响比较大的3个因素.

图5给出了热力管道直径D0和下沉率M这2个保温层设计几何参数对经济厚度差值Δδ的影响.由图5可以看出，随着D0和M的增大，Δδ越来越大，由式(2)和式(7)可知，这是由于D0和M的增大会增大修正前后的设计散热量差距，Δδ也会随之增大.从图5还可以发现，当D0较大时，Δδ随M增大而增加的速率也越来越大，由式(6)可知，这是由于D0较大时，相同下沉率M对应的下沉深度Lf增加，因此Δδ也会随之增大；当M较大时，Δδ随D0增大而增加的速率也越来越大，同样由式(6)可知，这是由于M较大时，相同的热力管道直径D0对应的下沉深度Lf增加，因此Δδ也随之增大.

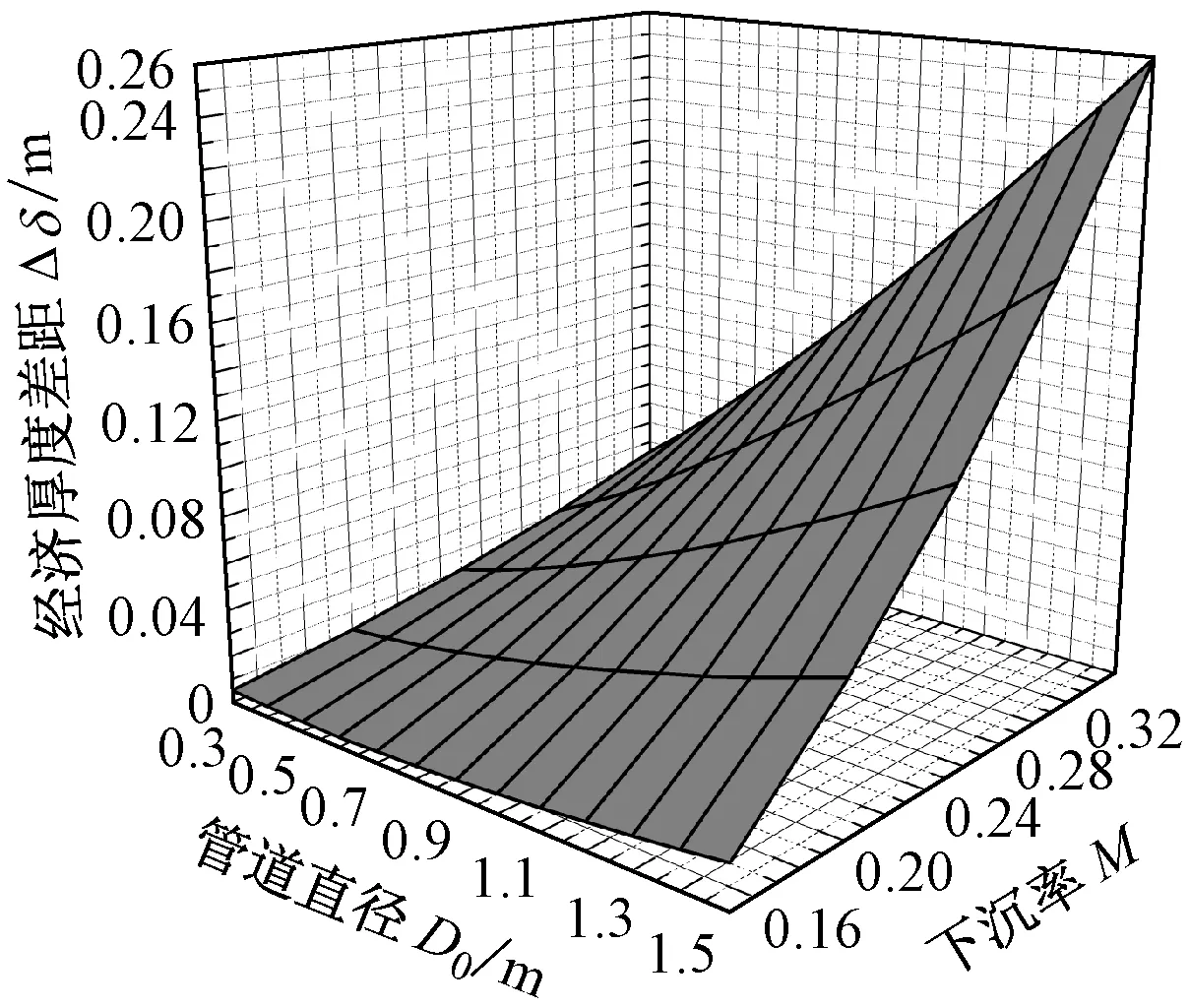
图5　管道直径和下沉率的影响Fig.5　Deviation of economic thickness vs. pipe diameter and sink rate

图6给出了管内介质温度T0对经济厚度差值Δδ的影响.从图6可以看出，随着管内介质温度从150 ℃升高到450 ℃，修正前后的经济厚度差值Δδ从0.225 m减小到0.013 m，由式(7)可知，这是由于介质温度下降后,保温层内外温差减小，修正前后的经济厚度都会变薄，相同下沉率M对应的下沉深度Lf减小，因此Δδ也会随之减小.

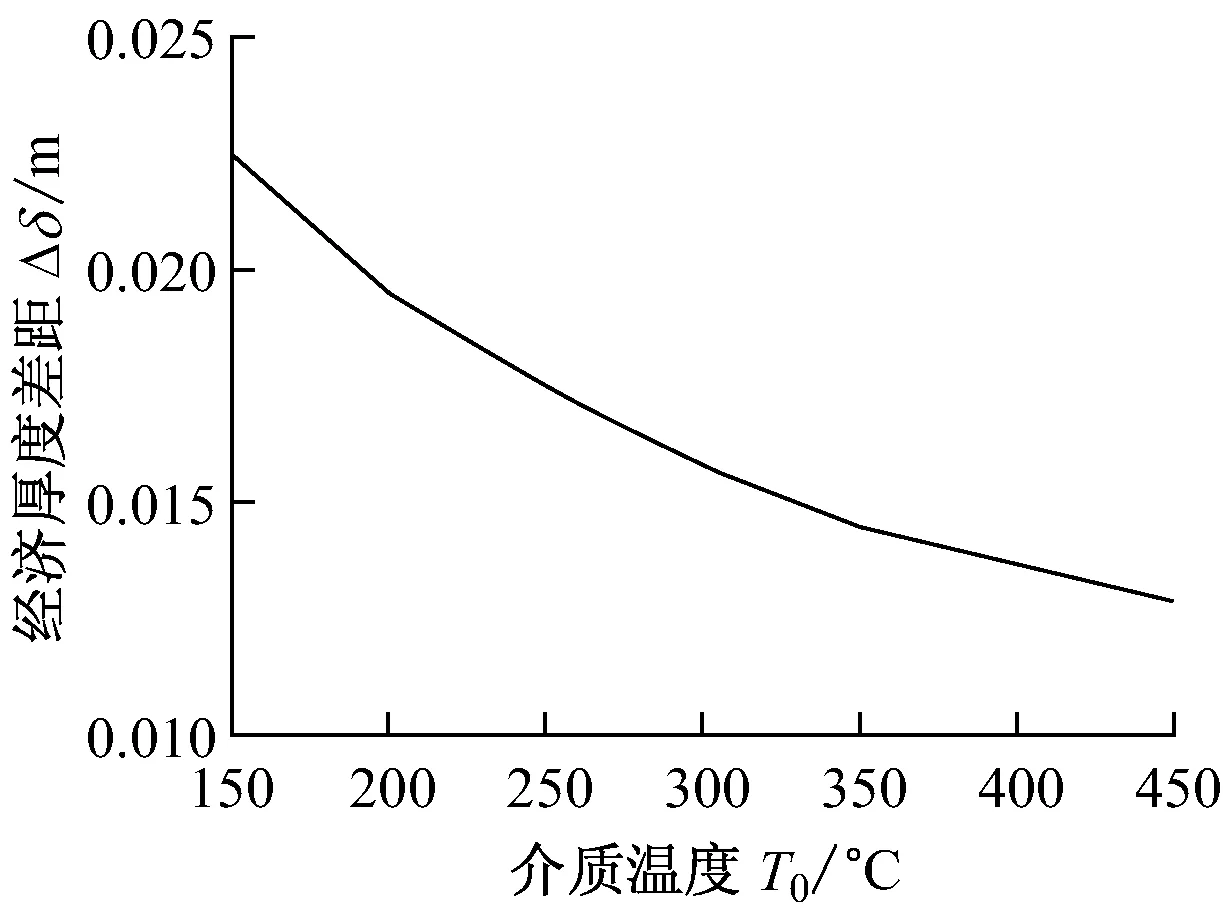
图6　热力管道介质温度的影响Fig.6　Deviation of economic thickness vs. steam temperature

2.2.2经济学参数的影响

由图(1)可知，经济厚度法的年总费用由初始投资的年分摊费用和年散热费用2部分组成，因此这2部分费用对于修正前后的经济厚度差值Δδ也会产生影响.在经济厚度法的各项经济参数中，保护层造价Pp、初始投资年分摊利率S和热价Pe对经济厚度差值Δδ的影响较大.

图7反映了保护层造价Pp和初始投资年分摊利率S这2个初始投资的设计参数对经济厚度差值Δδ的影响.从图7可以看出，经济厚度差值Δδ随着保护层造价Pp的增加而不断增大，并且增大幅度慢慢变小，经济厚度差值Δδ随着初始投资年分摊利率S的增加也呈现出相同的变化规律.由图1所示的经济厚度法原理可知，这是由于保护层造价Pp和初始投资年分摊利率S的增加都会导致相同保温层厚度的热力管道的初始投资年分摊费用增加，经济厚度变薄，进而导致散热量增加，修正前后的散热量差也随之增加，最终使经济厚度差值Δδ变大，随着保护层造价Pp和初始投资年分摊利率S的增加，经济厚度差值Δδ变大的幅度逐渐减小.

图8反映了热价Pe对经济厚度差值Δδ的影响.由图8可知，随着热价Pe的增加，经济厚度差值Δδ逐渐减小，这是由于热价的增加会导致保温层厚度增加，管道散热量减小，修正前后的散热量差距也随之减小，最终导致Δδ减小.

图7　保护层造价和初始投资年分摊利率的影响Fig.7　Deviation of economic thickness vs. insulation cost and the annual interest rate

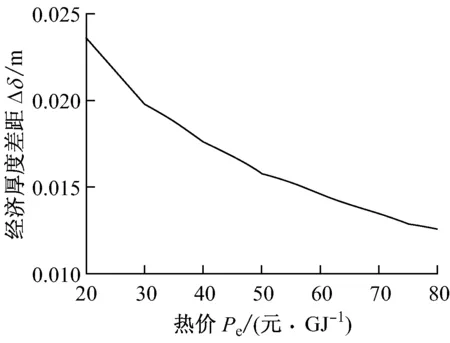
图8　热价的影响Fig.8　Deviation of economic thickness vs. heat price

2.2.3其他参数的影响

笔者还计算了保温材料种类、保温层价格Pi和环境温度Ts等因素对修正前后经济厚度差值的影响.结果表明：采用不同材料导致的Δδ的变化在0.005 m以内；保温层价格Pi从200元/m3增加到800元/m3时，Δδ只增加了0.001 7 m；环境温度Ts从10 ℃升高到40 ℃时，Δδ增加了0.005 m.因此，这3个因素对修正前后经济厚度差值Δδ的影响不大.

3　结　论

(1) 在热力管道保温层设计过程中考虑保温材料下沉的影响后，设计所得保温层厚度变厚，漏热损失明显下降，最终年总费用降低.

(2) 当热力管道直径D0、下沉率M和管内介质温度T0在适当范围内变化时，考虑保温材料下沉前后的经济厚度差值Δδ会发生0.01 m到0.1 m不等的变化，修正前后的设计厚度之差受这些因素影响会发生比较明显的变化；在经济学参数中，保护层造价Pp、初始投资年分摊利率S和热价Pe在适当范围内的变化会导致Δδ发生0.01 m左右的变化，也会对修正前后的设计厚度之差产生比较明显的影响.

[1]OZKAHRAMAN H T, BOLATTURK A. The use of tuff stone cladding in buildings for energy conservation[J]. Construction and Building Materials, 2006, 20(7): 435-440.

[2]KAYNAKLI O. Economic thermal insulation thickness for pipes and ducts: a review study[J]. Renewable and Sustainable Energy Reviews, 2014, 30: 184-194.

[3]中华人民共和国住房和城乡建设部. GB 50264—2013 工业设备及管道绝热工程设计规范[S]. 北京: 中国计划出版社, 2013.

[4]中华人民共和国国家发展和改革委员会. DL/T 5072—2007 火力发电厂保温油漆设计规程[S]. 北京: 中国电力出版社, 2007.

[6]SAHIN A Z, KALYON M. Maintaining uniform surface temperature along pipes by insulation[J]. Energy, 2005, 30(5): 637-647.

[8]艾振宙. 管道保温结构的优化设计研究[D]. 长沙: 长沙理工大学, 2010.

[9]吴双应, 李友荣, 陈凌霜. 管道保温层经济厚度计算[J]. 石油化工设备, 2001, 30(3): 17-19.

WU Shuangying, LI Yourong, CHEN Lingshuang. Calculation of economical thickness for pipe insulation[J]. Petro-chemical Equipment, 2001, 30(3): 17-19.

[10]HOLMAN JP. Heat transfer[M]. 9thed. New York, USA: McGraw-Hill Book Company, 2002: 83-87.

Influence of the Sink of Insulation Materials on Design of the Insulation Layer for Horizontal Circular Heating Pipelines

ZHAOXu,SHENQie,ZHANGNing,SUNDaming,ZOUJiang

(School of Energy Engineering, Zhejiang University, Hangzhou 310027, China)

Influence of the sink of insulation materials on calculation of the economic insulation thickness over horizontal circular heating pipelines was quantatively analyzed, based on which a correction method was proposed for the design of economic insulation thickness by simultaneously analyzing the heat path of the whole insulation layer. The numerical method of economic thickness was studied theorectically, and the effects of design parameters on the economic thickness was researched by varying the parameters in an acceptable range. Using the corrected numerical method of economic thickness, the insulation for heating pipelines actually operated in Huangtai Power Plant was designed. Results show that the annual insulation expense may be reduced by 0.7% after the insulation is designed by the corrected numerical method of economic thickness. The diameter of heating pipelineD0, the sink rateMand the medium temperatureT0inside the pipeline are all the main factors influencing the design of the economic insulation thickness.

power plant; heating pipeline ; heat dissipation; insulation; economic thickness method

2015-11-05

2015-12-16

国家自然科学基金资助项目(51476136)

赵旭(1991-)，男，湖北荆门人，硕士研究生，主要从事热力管道保温方面的研究.

孙大明(通信作者)，男，博士生导师，电话(Tel．)：13064718689；E-mail：sundaming@zju.edu.cn．

1674-7607(2016)09-0759-06

TK01+8

A学科分类号：470.10