无速度传感器DFIG最大风能捕获终端滑模优化控制

吴忠强，　王昕懿，　赵习博

(燕山大学 电气工程学院，工业计算机控制工程河北省重点实验室，河北秦皇岛 066004)



无速度传感器DFIG最大风能捕获终端滑模优化控制

吴忠强，王昕懿，赵习博

(燕山大学 电气工程学院，工业计算机控制工程河北省重点实验室，河北秦皇岛 066004)

针对双馈风力发电机(DFIG)这类复杂的强耦合、非线性系统，利用Backstepping终端滑模设计控制器实现最大风能捕获.采用微分跟踪器(TD)安排参考输入信号，解决初始误差大的问题.基于电流方程设计扩张状态观测器(ESO)，对磁链和转速进行估计，以降低磁链和转矩脉动，实现无传感器运行，并对耦合等扰动项进行观测且加以补偿，从而简化Backstepping终端滑模控制器的设计.针对控制器和观测器中待整定参数较多的问题，利用萤火虫算法(FA)进行参数寻优.结果表明：该方案能够实现无静差跟踪，提高了系统的控制精度.

双馈风力发电机； 最大风能捕获； Backstepping终端滑模控制； 扩张状态观测器； 萤火虫算法

双馈风力发电机(DFIG)具有可调节功率因数、调速范围宽、控制方式灵活和柔性连接等优点，在风力发电系统中被广泛应用[1].

DFIG是一个多变量、强耦合的非线性系统，欲实现对其高性能控制，必须克服不确定因素和非线性对系统性能的影响[2].传统的PI控制器适合于线性定常系统，具有结构简单、稳定性较好的优点，但其鲁棒性差，在调速范围要求较宽的情况下，无法同时满足响应快速、稳态精度高的要求[3].针对这一问题，非线性控制器被广泛关注.Fu等[4]采用模糊逻辑对DFIG进行控制器设计，实验结果表明与传统的PI和PID控制器相比，模糊控制器电流响应快，几乎没有稳态误差，但其模糊规则、量化因子和比例因子需要反复试凑才能确定，增加了工作量.卫志农等[5]引入自抗扰控制技术，建立了转子电流自抗扰控制模型，仿真结果表明，在风速变化时，自抗扰控制比PID控制具有更小的超调量和更快的响应速度，对电网电压的波动也有较好的抑制能力，但是存在静差和稳态精度不高等问题.Bekakra等[6]提出了一种滑模控制策略，实现定子与电网之间的能量转换，仿真结果表明，滑模控制能实现无静差跟踪，但是系统存在明显的抖振现象.

为了实现最大风能捕获，需在DFIG轴上安装速度检测装置，导致系统成本提高，系统可靠性降低，因此，DFIG的无速度传感器研究逐渐成为热点问题[7].Pattnaik等[8]采用模型参考自适应观测器对转速进行估计，该方法在较大调速范围内性能较好，但在低速时受参数变化影响较大.Benbouzid等[9]采用高阶滑模观测器估计电机转速，在有限时间内，能够对状态变量进行精确观测，但是高阶滑模的设计过程复杂，降低了系统的实用性.Bezza等[10]采用最大功率点跟踪的方法，在无速度传感器情况下实现DFIG的最大风能捕获，但系统的抗扰能力不强.Zhang等[11]用转子电流参考分量代替实际电流分量，简化了观测器的设计，但无自动纠偏能力，系统精度低.

笔者基于Backstepping方法设计终端滑模控制器以实现最大风能捕获，不仅能够实现无静差跟踪，而且具有很强的抖振抑制能力.采用微分跟踪器(TD)安排参考输入信号，解决初始误差大的问题.设计扩张状态观测器(ESO)对DFIG的转子角速度和磁链进行估计，同时估计扰动项(耦合项)，不仅省去了测速装置，降低了造价，还对估计出的扰动项加以补偿，省去复杂的解耦过程.由于需要整定的参数很多，采用萤火虫算法(FA)对参数进行寻优，使控制器和观测器都工作在最佳状态，进一步提高控制精度.

1　DFIG数学模型

DFIG在两相同步旋转坐标系下的状态方程[12]如下:

(1)

转矩方程：

(2)

齿轮箱功率方程：

(3)

式(1)～式(3)中各变量的含义见文献[12].

2　最大风能捕获

根据Betz理论[12]有：

(4)

式(4)中各参数的含义见文献[12].

风能捕获系数[13]：

(5)

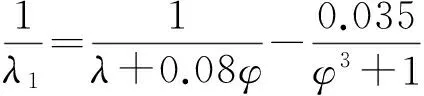
由式(5)可知，Cp与λ、φ有关.为验证所设计的观测器及控制器在DFIG上的应用效果，只考虑采用控制DFIG转速实现最大风能捕获的情况，不考虑风轮机叶片桨距角的影响，即令φ=0°，根据最佳叶尖速比λopt可以得到不同风速下的风轮最佳角速度ωfopt=λoptν/R，进而得到DFIG转子最佳角速度ωropt=nfωfopt，将其作为转子角速度参考值.

当风力机实现最大风能捕获时，风力机最佳输出功率Pmopt与风轮角速度ωf的关系[12]为

(6)

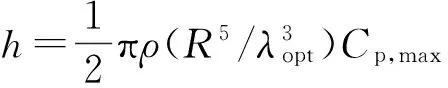
DFIG的最佳输入转矩Tmopt与转子角速度ωr的关系为

(7)

3　TD设计

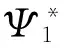
(8)

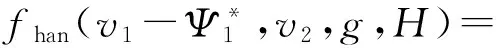
Y=M1+Hv2，

l0=Hl，

l=gH，

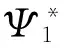
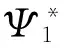
相应的跟踪误差变为

(9)

(10)

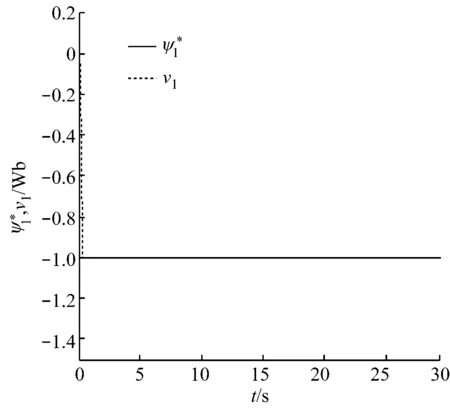
图1　v1与的对比曲线图Fig.

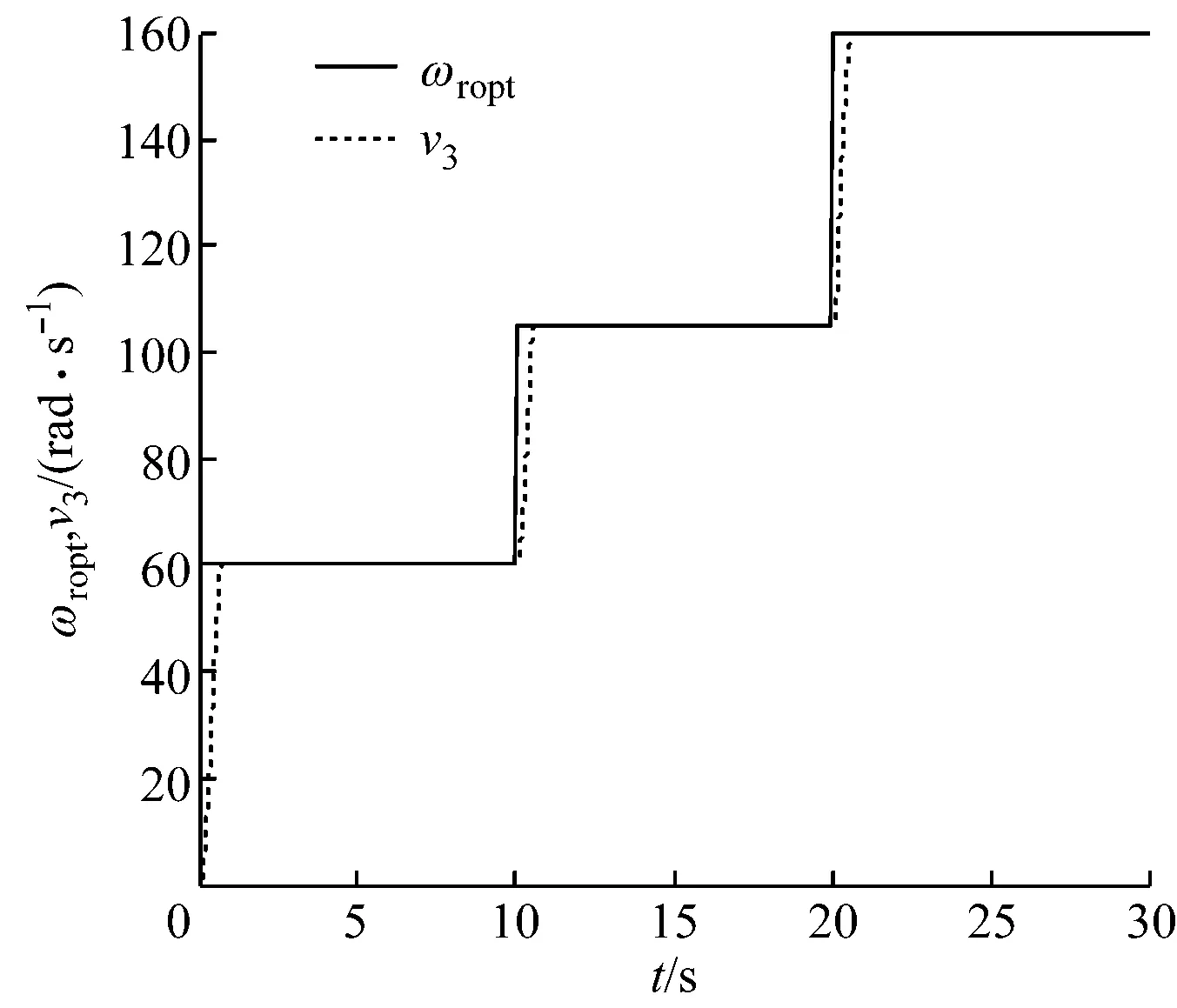
图2　v3与ωropt的对比曲线图Fig.2　Comparison between v3 and ωropt

4　ESO的设计

对ird和irq分别设计ESO.

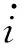
(11)

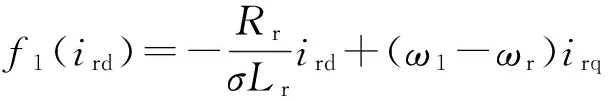
式(11)所示1阶系统的ESO数学模型为

(12)

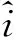
fal(·)为非线性函数，其表达式为

(13)

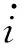
(14)

其中，

式(14)所示1阶系统的ESO数学模型为

(15)

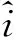
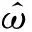
(16)

5　Backstepping终端滑模控制器设计

设计步骤是把式(1)的系统划分成2个子系统分别设计终端滑模控制器.首先考虑子系统1：

(17)

先利用ESO观测的总扰动估计值m2进行补偿，可省略解耦以简化后续控制器的设计，其原理框图如图3所示.

图3　扰动项补偿原理图Fig.3　Principle diagram of compensation for perturbed terms

补偿后的系统如下：

(18)

令z2=ird-α1(Ψ1)

(19)

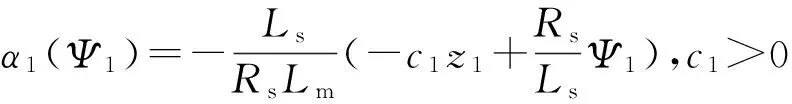
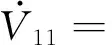
(20)

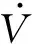
为使z2在有限时间内收敛到零，从而提高系统的收敛速度和稳态跟踪精度，对z2构成的子系统设计如下非奇异终端滑模面：

(21)

式中：p,q为奇数，1

0.

设计如下控制律：

(22)

(23)

(24)

式中：η1为设计参数，η1>0.

则子系统1的状态在有限时间收敛.

根据Backstepping算法，定义如下Lyapunov函数：

对时间求导，得：

(25)

由于

(26)

将式(22)和式(23)代入式(26)得：

(27)

对时间再求一次导：

(28)

将式(24)代入式(28)得：

(29)

将式(29)代入式(25)得：

(30)

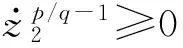
下面考虑子系统2：

(31)

同理，利用ESO观测的总扰动估计值m4进行补偿，可省略解偶以简化后续控制器的设计，补偿后的系统如下：

(32)

令z4=irq-α2(ωr)

(33)

其中，α2(ωr)为中间控制量，

(34)

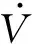
(35)

式中：γ2为常数，γ2>0.

设计如下控制律：

(36)

(37)

(38)

式中：η2为设计参数，η2>0.

则子系统2的状态在有限时间内收敛.

采用Backstepping算法，定义如下Lyapunov函数：

对时间求导，得：

(39)

由于

(40)

将式(36)和式(37)代入式(40)得：

(41)

对时间再求一次导，得：

(42)

将式(38)代入式(42)得：

(43)

将式(43)代入式(39)得：

(44)

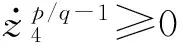
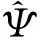
6　FA优化

由于待设计的参数较多，2个ESO有4个参数β01、β02、β03和β04需要整定，终端滑模控制器有6个参数c1、c2、γ1、γ2、η1和η2需要整定.采用FA对这些参数进行在线实时寻优.

6.1FA的数学描述及建模

萤火虫算法具有计算速度快、概念简明、需要设置的参数少和容易实现等优点.萤火虫算法的核心思想是萤火虫被绝对亮度比它大的萤火虫吸引，并根据位置更新公式、更新自身位置[15-17].

假设萤火虫i的绝对亮度比萤火虫j的绝对亮度大，则j被i吸引而向i移动.因此，为了对萤火虫i对j的吸引力进行建模，首先要对萤火虫i对j的相对亮度建模.综合外界因素，可以定义萤火虫i对j的相对亮度为

(45)

式中：ξ为光吸收系数，可设为常数，ξ=50；dij为i对j的距离.

(46)

假设i对j的吸引力与i对j的相对亮度成比例，则由萤火虫i相对亮度的定义，可得i对j的吸引力χij(dij).

(47)

式中：χ0为最大吸引力，即在d=0处萤火虫的吸引力，可取χ0=1.

由于被i吸引，j向其移动而更新自己的位置，j的位置更新公式如下：

(48)

式中：t为算法的迭代次数；Γi、Γj分别为i和j所处的空间位置；κj是由高斯分布、均匀分布或者其他分布得到的随机向量.

6.2FA的基本流程

FA流程图如图4所示.

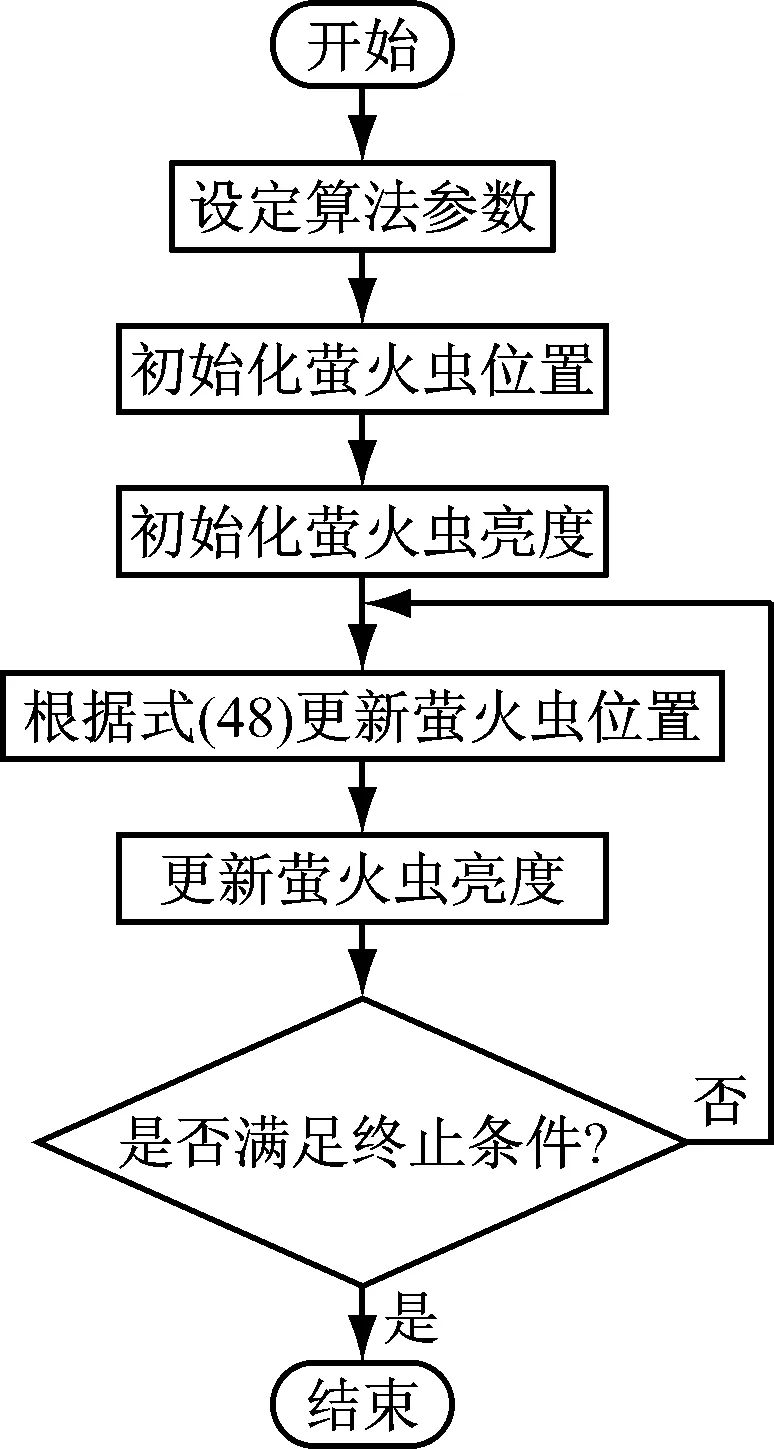
图4　FA流程图Fig.4　FA flow chart

整个控制系统结构图如图5所示.

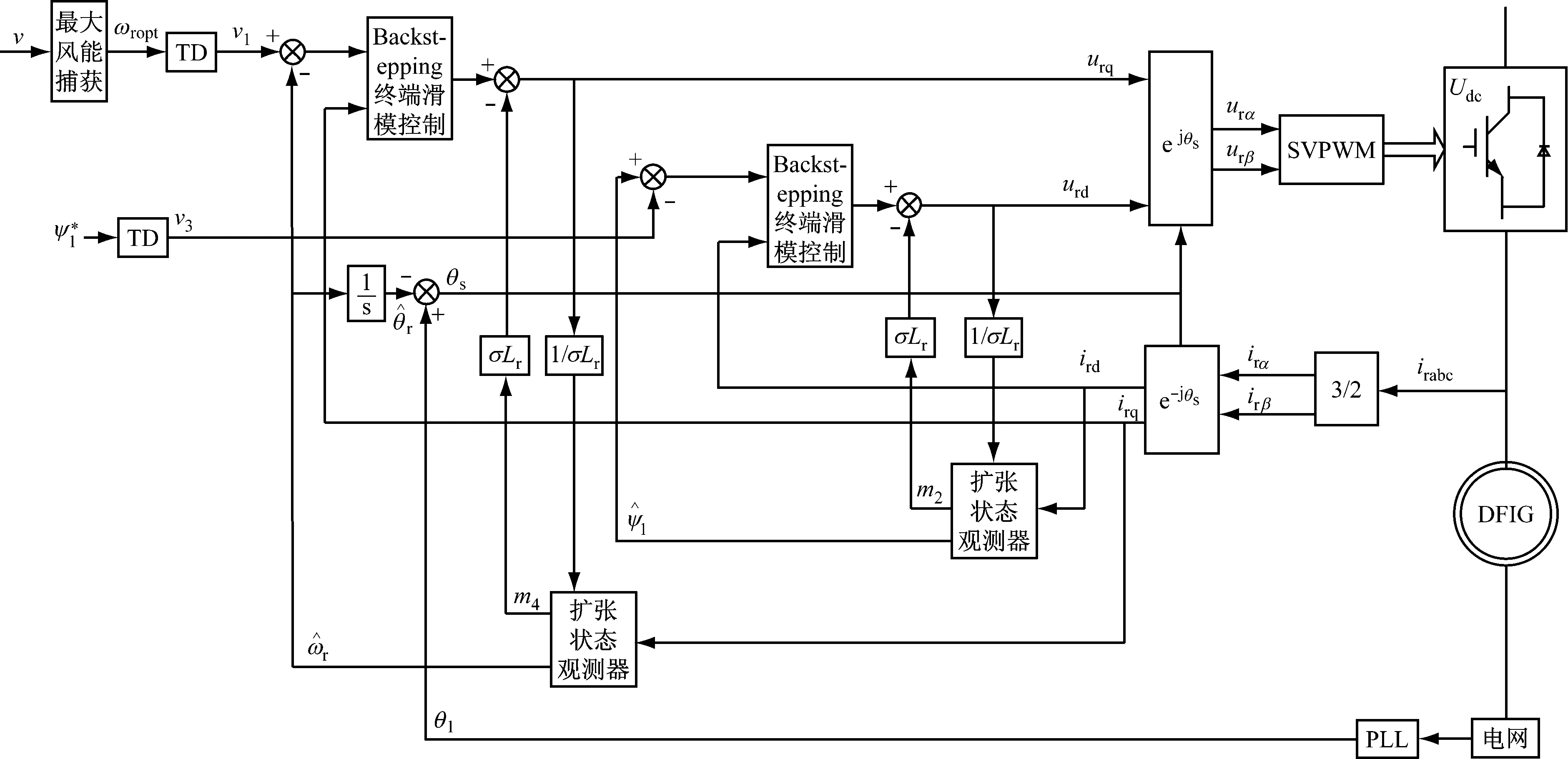
图5　DFIG控制系统原理框图Fig.5　Block diagram of DFIG control system

7　仿真研究

7.1参数设置

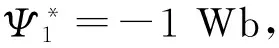
7.2仿真结果及分析

案例1：为了验证所提方案的有效性，在恒定风速情况下，对系统进行仿真研究.风速曲线如图6所示，系统的各状态变量曲线如图7所示.

由图7(a)～图7(c)可以看出，采用本文中的观测器及控制器，角速度及电流的暂态过程快、无超调，稳态误差小于10-3，抑制了抖振，在有限时间内实现无静差跟踪，提高了系统的控制精度.

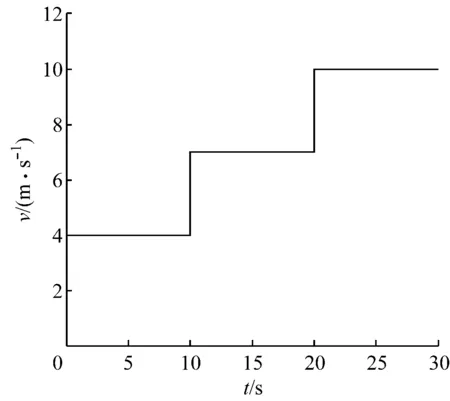
图6　恒定风速曲线Fig.6　Curve of constant wind speed

由图7(d)和图7(f)可知，0～10 s的转速为亚同步转速；10～20 s的转速接近同步转速，20 s以后的转速为超同步转速.在转速接近同步转速时，转子处于直流励磁状态；在亚同步转速和超同步转速时，转子电流反相，而定子电流频率始终与电网频率相同，符合变速恒频控制要求，体现了交流励磁变速恒频DFIG发电系统固有的、与发电机运行速度无关的优良“柔性”并网性能.

根据定子有功功率曲线图7(f)，分析在给定风速下最大风能捕获的实现：(a)同步转速时的情况.根据DFIG的运行原理，此时风力机捕获的最大风能全部转化为定子输出的电能，转子电能只用于铜耗.由式(6)可计算出风力机捕获的最大风功率为6.12 kW，由图7(f)可得定子输出的有功功率为5.45 kW，两者相近，符合DFIG的运行原理，且实现最大风能捕获.(b)亚同步转速时的情况.此时风力机捕获的最大风能和转子的电能一同转化为定子的输出电能.同样得出风力机捕获的最大风功率为1.14 kW，同样得定子输出的有功功率为2.98 kW，定子输出的有功功率大于风力机捕获的最大风功率，说明转子为定子提供了电功率.(c)超同步转速时的情况.此时风力机捕获的最大风能转化为转子的电能和定子的电能.风力机捕获的最大风功率为21.64 kW，定子输出的有功功率为8.75 kW，风力机捕获的最大风功率大于定子输出的有功功率，说明风力机为转子提供了电功率.以上情况均符合DFIG的运行原理，且实现了最大风能捕获.

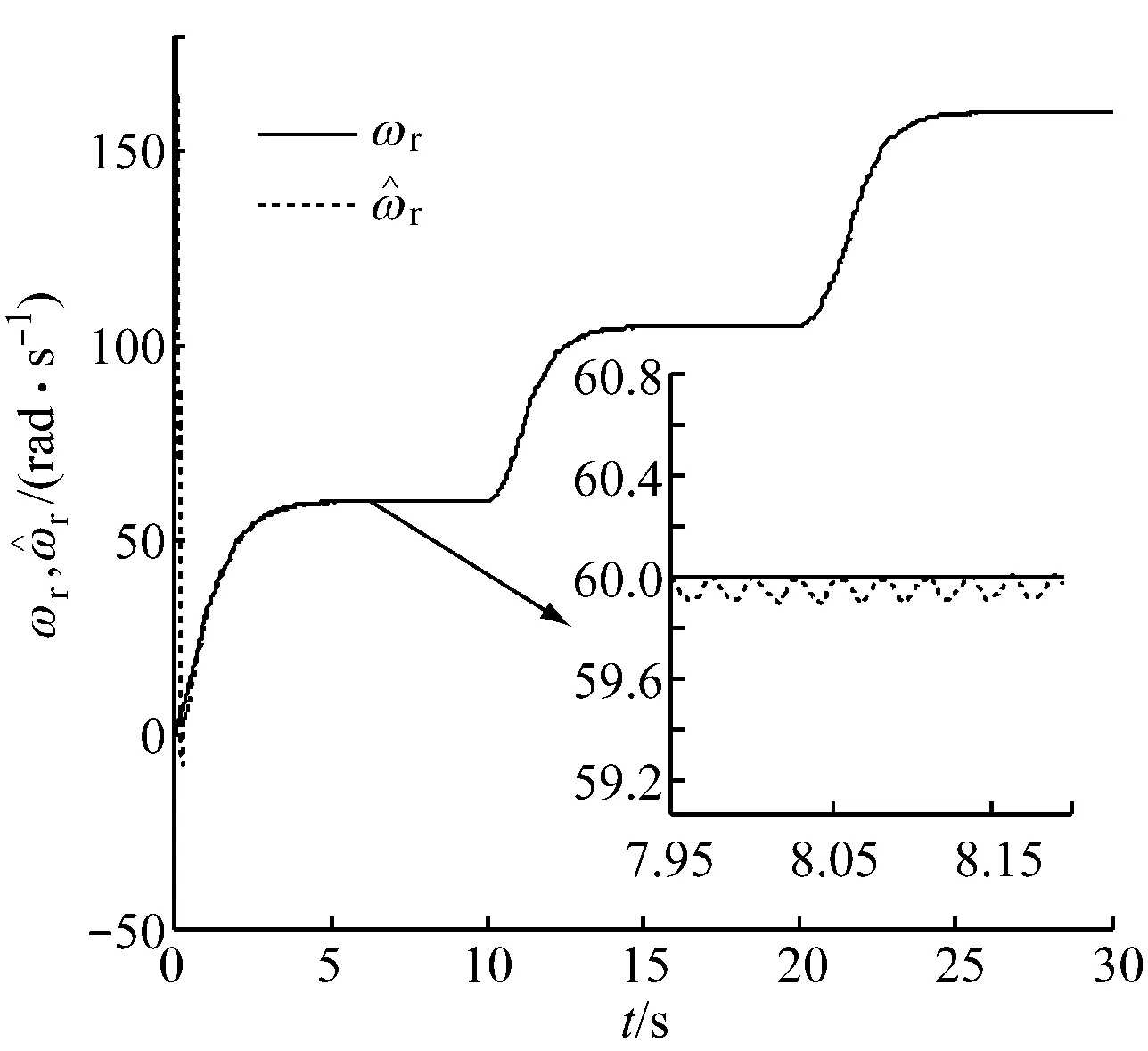
(a) ωr和曲线

(b) ird和的曲线

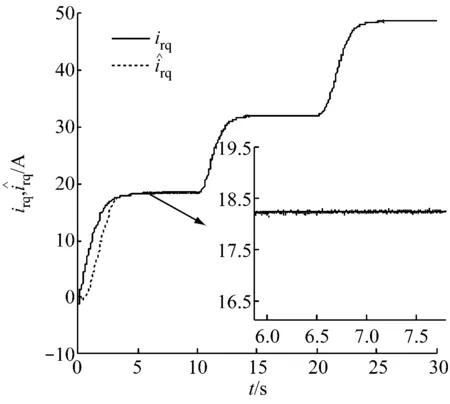
(c) irq和曲线

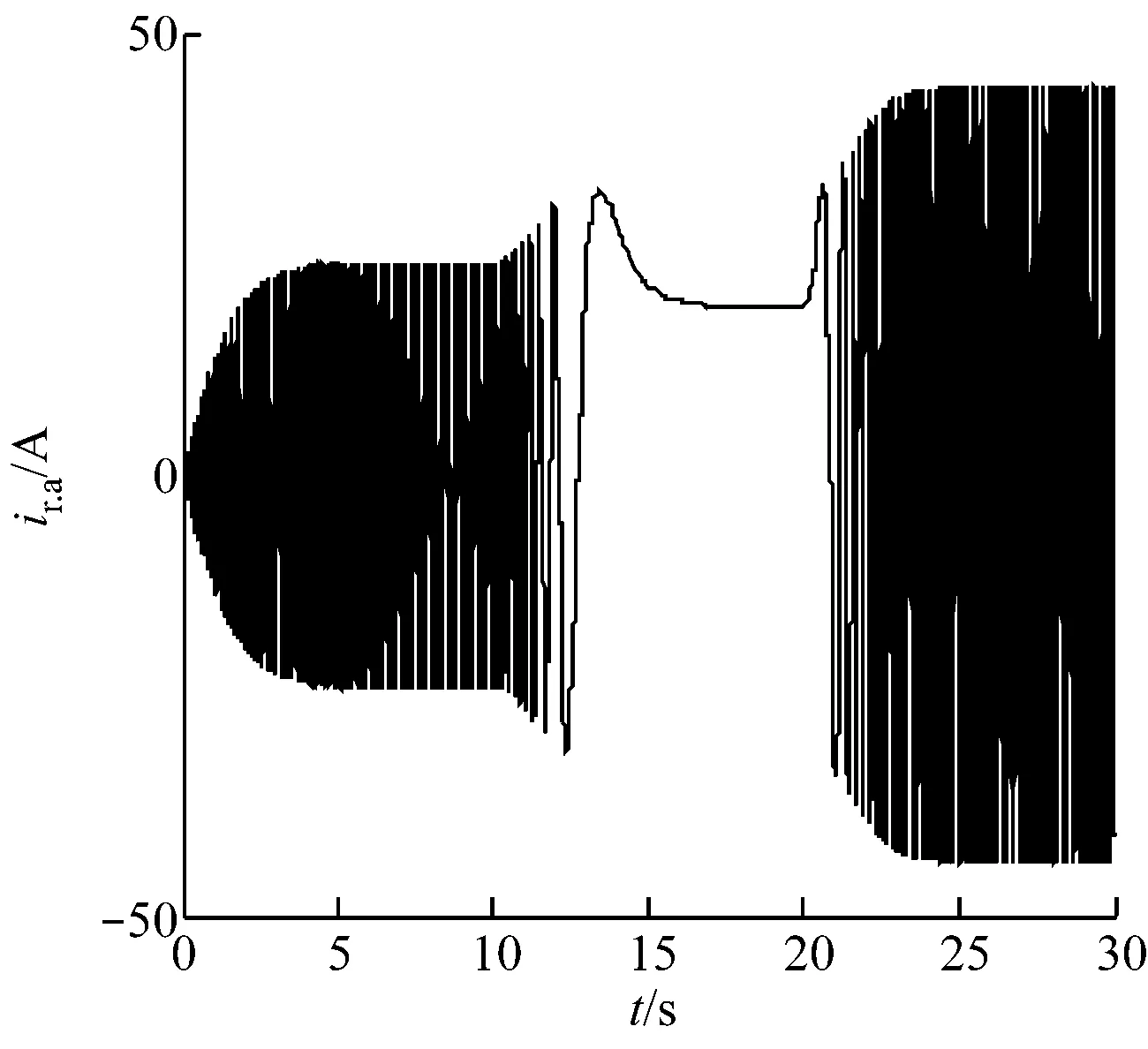
(d) 转子a相电流曲线

(e) 定子a相电流曲线

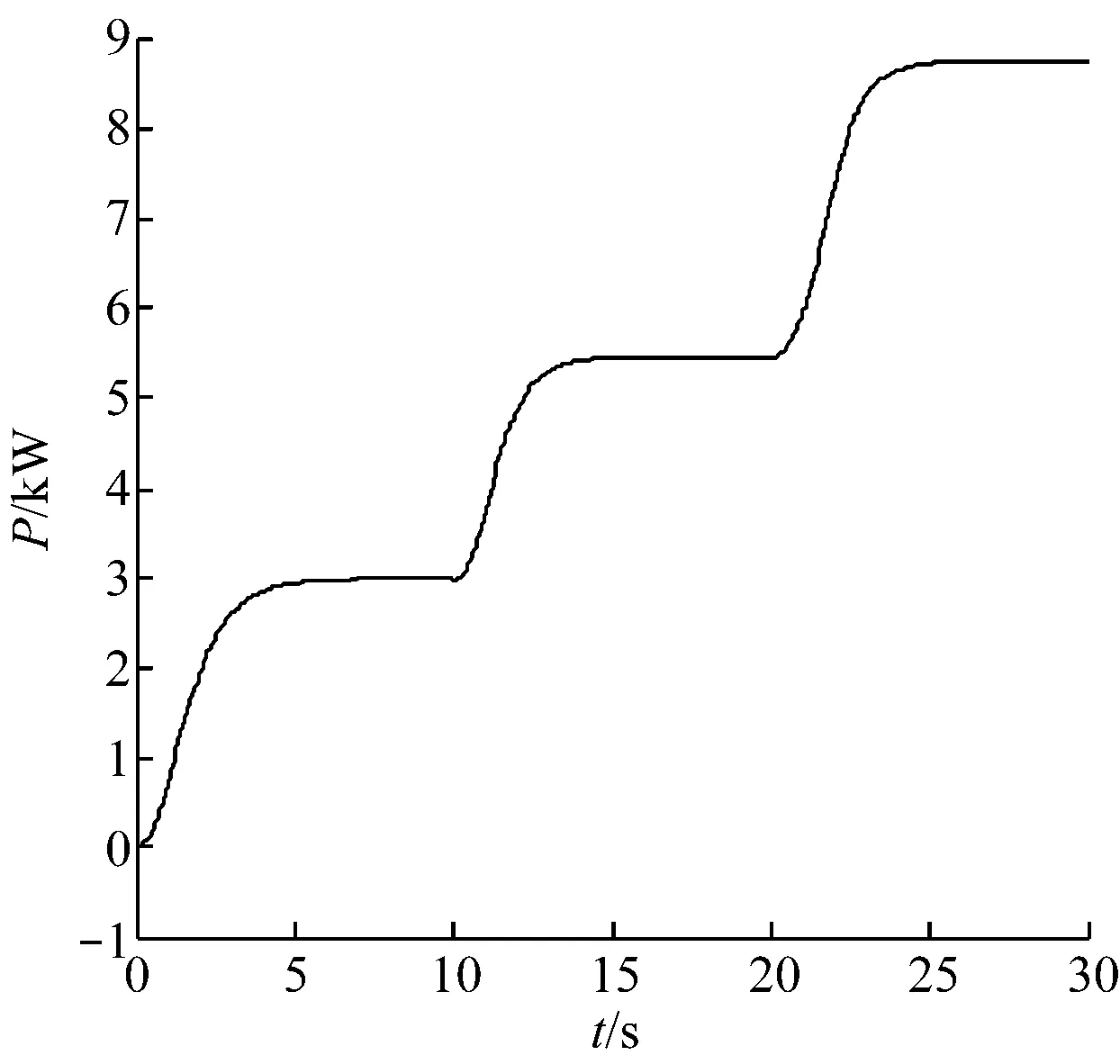
(f) 定子有功功率曲线图7　恒定风速下各状态变量曲线Fig.7　Curves of different state variables at constant wind speed

以上均为考虑给定风速小于风力机最大运行风速时的情况，即Cp恒定区.随着风速增大，发电机将达到其极限转速，即进入转速恒定区，发电机转速保持恒定，其功率在达到极限值之前一直增大.当发电机达到其功率极限值时，系统进入功率恒定区，随着风速的增大，发电机转速降低，使Cp值降低，从而保持功率不变.

图8　文献[5]中ωr和曲线Fig.

图8中给出的是转速标幺值，与图7比较可以看出，文献[5]的方案中暂态过程波动明显，且有稳态误差.本文方案中暂态过程波动非常小，且无静态误差，跟踪精度高.

案例2：由于滑模控制在滑模面内对系统参数变化有鲁棒性，在以下2种情况下对终端滑模控制系统进行仿真验证，分别得到观测转速与实际转速的误差Δωr曲线和角度误差Δθ曲线：(1)当Rs和Rr不变，Ls、Lr和Lm分别增加20%时，Δωr曲线如图9所示；(2)当Ls、Lr和Lm不变，Rs和Rr分别增加20%时，Δωr曲线如图10所示.图11为案例1的观测转速与实际转速的误差Δωr曲线.

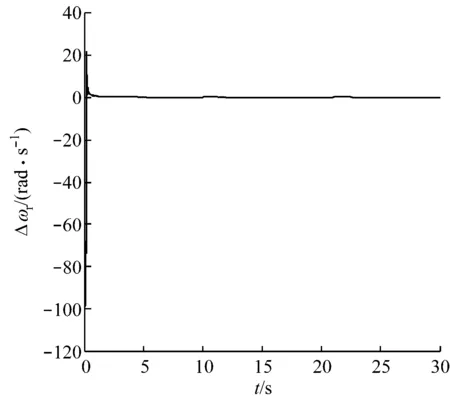
图9　Ls、Lr和Lm分别增加20%时的Δωr曲线Fig.9　Curve of Δωr with 20% increase of Ls, Lr and Lmrespectively

由图9～图11可以看出，由于滑模控制在滑模面内对系统参数变化有较强的自适应能力，当电机电阻或电感值发生较大变化时，仍能将角速度误差控制在允许范围内.

案例3:考虑实际应用情况，对随机风速下的系统进行仿真.随机风速曲线如图12所示，系统的各状态变量曲线如图13所示.

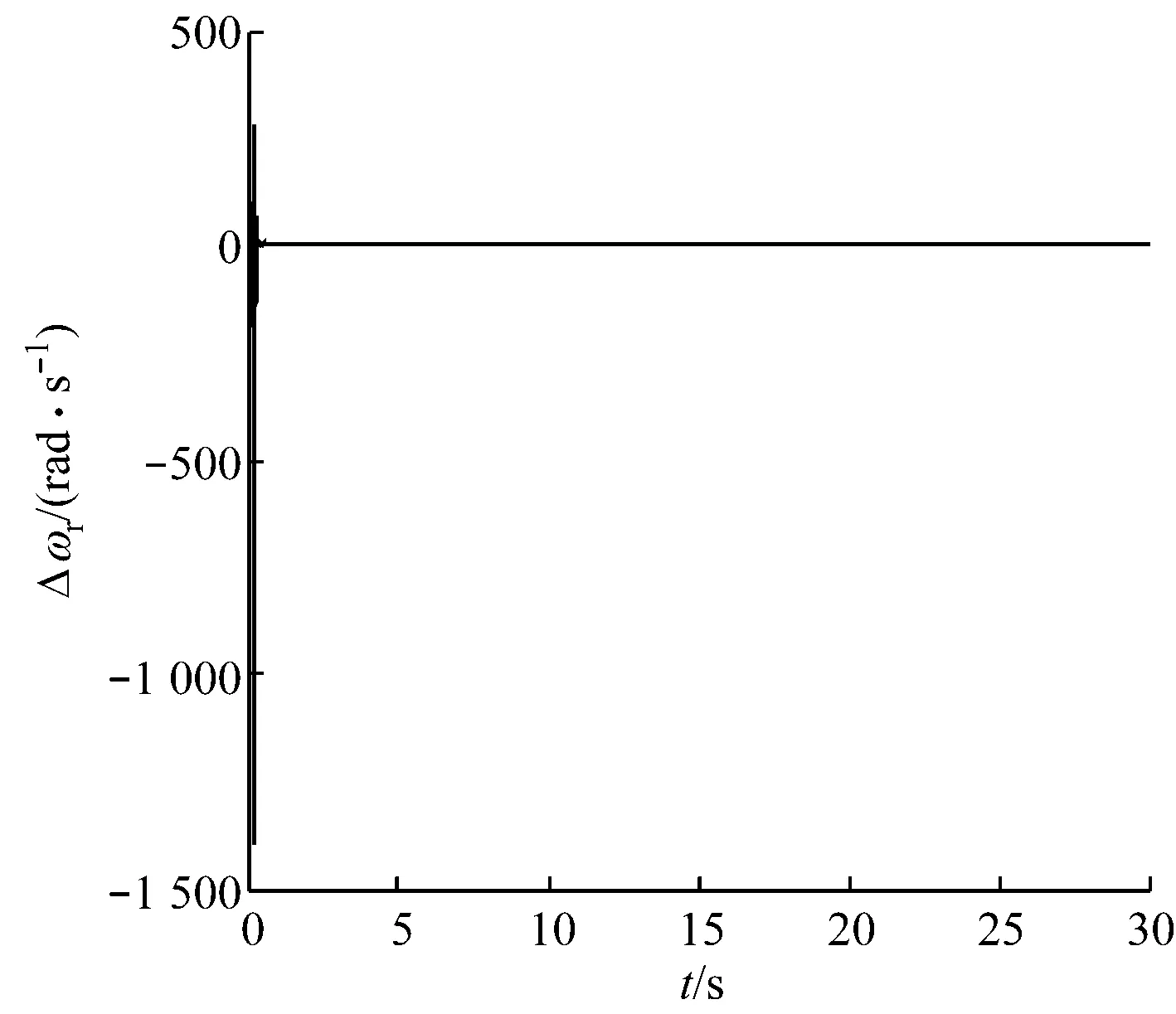
图10　Rs和Rr分别增加20%时的Δωr曲线Fig.10　Curve of Δωr with 20% increase of Rs and Rr respectively

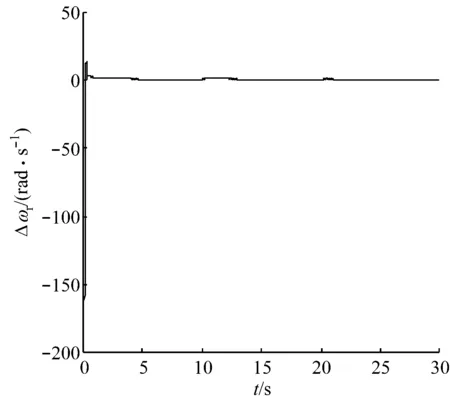
图11　案例1的Δωr曲线Fig.11　Curve of Δωr in example 1

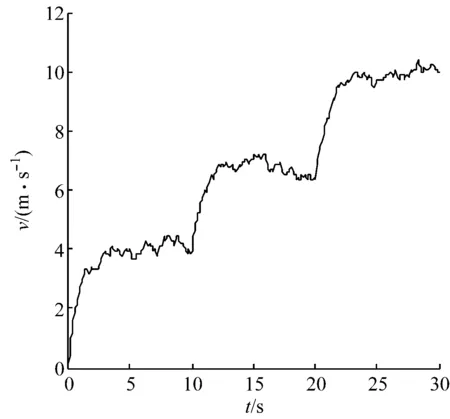
图12　随机风速曲线Fig.12　Curve of random wind speed

由图13可知，在随机风速情况下，采用本文中的观测器及控制器，仍能很好地实现最大风能捕获，符合变速恒频控制要求.

8　结　论

针对DFIG系统，设计Backstepping终端滑模控制器，实现最大风能捕获.该系统不仅能够快速收敛和高精度跟踪，而且具有去除抖振和较强的抗干扰能力.采用TD安排参考输入信号，解决初始误差大的问题.采用ESO不仅省去了测速装置，还解决了解耦问题，简化了Backstepping滑模控制器的设计.FA解决了系统多参数整定的问题.仿真验证具有良好的控制效果.

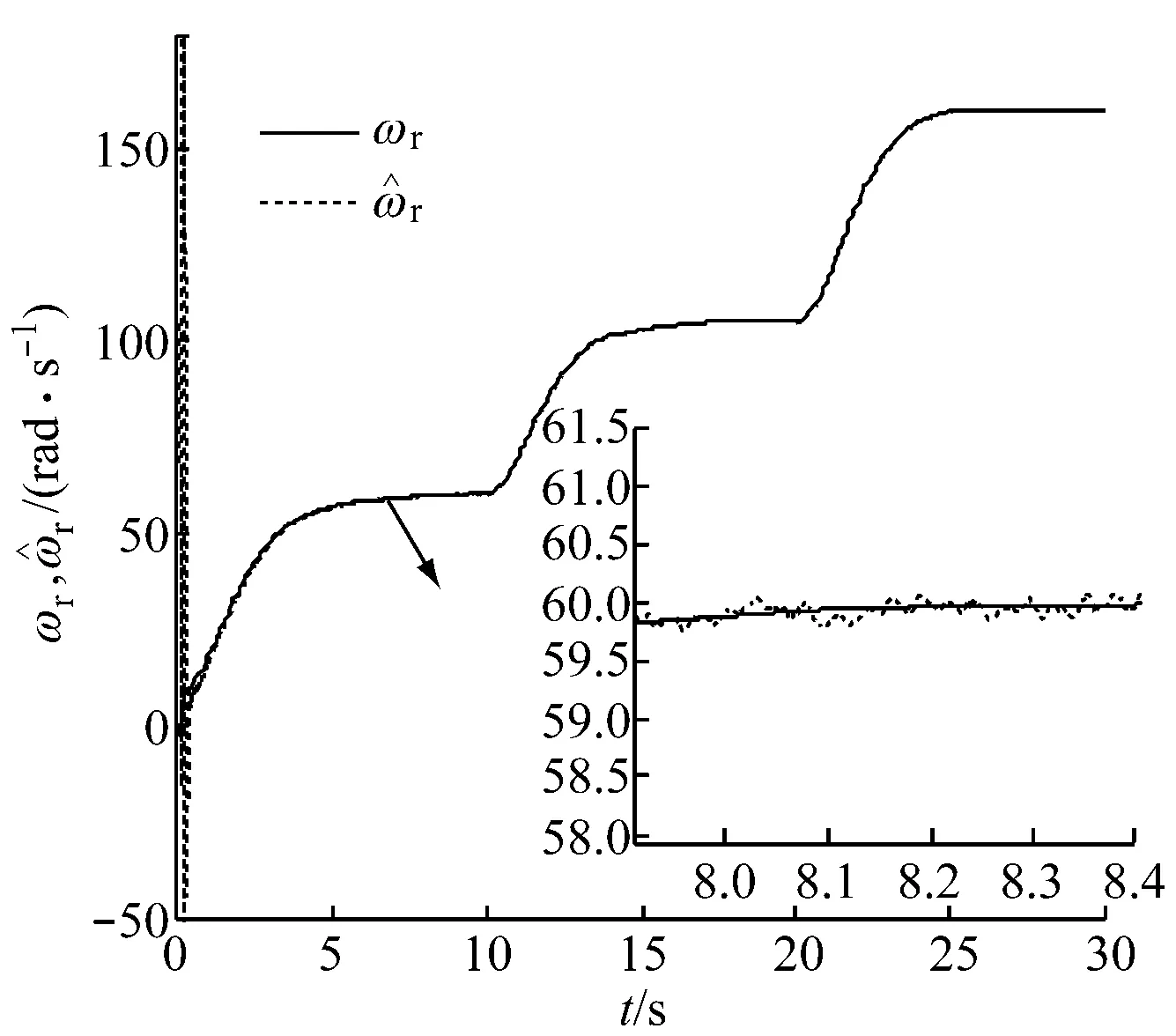
(a) ωr 和曲线

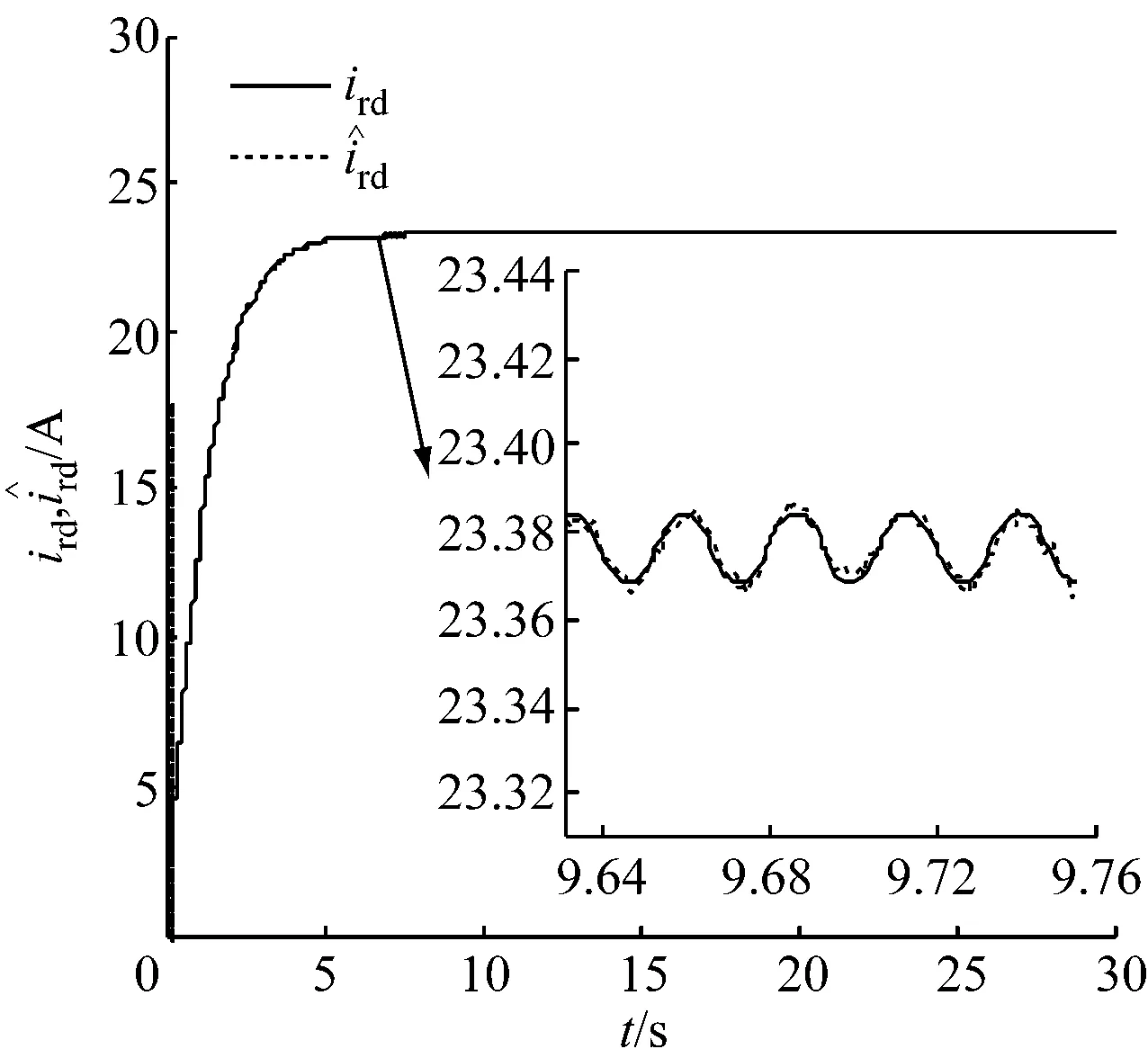
(b) ird和曲线

曲线

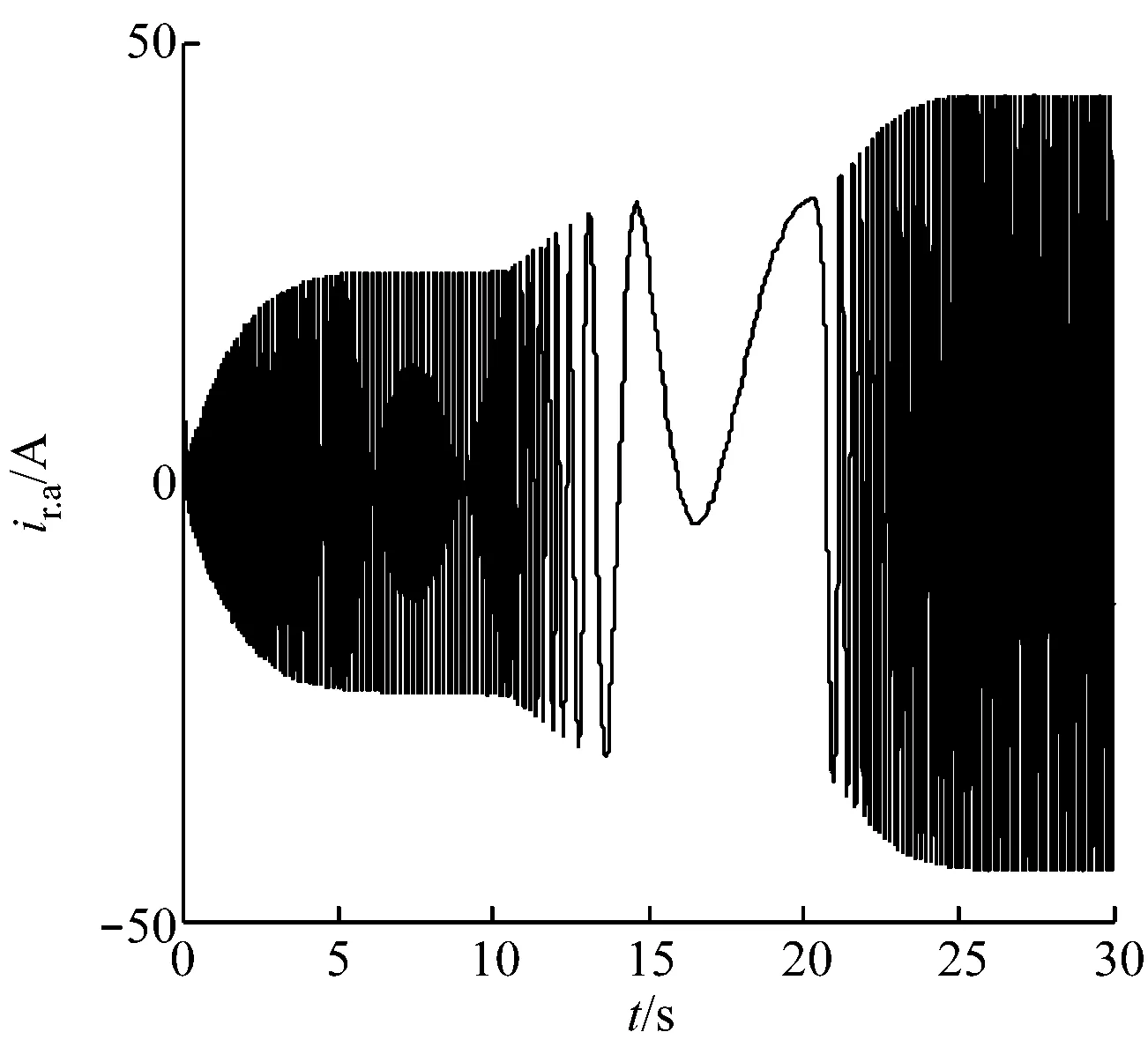
(d) 转子a相电流曲线

(e) 定子a相电流曲线图13　随机风速下各状态变量曲线Fig.13　Curves of different state variables at random wind speed

[1]LIU Xiangjie, KONG Xiaobing. Nonlinear model predictive control for DFIG-based wind power generation[J]. IEEE Transactions on Automation Science and Engineering, 2014, 11(4): 1046-1055.

[2]BELMOKHTAR K, DOUMBIA M L, AGBOSSOU K. Novel fuzzy logic based sensorless maximum power point tracking strategy for wind turbine systems driven DFIG (doubly-fed induction generator)[J]. Energy, 2014, 76: 679-693.

[3]GAYEN P K, CHATTERJEE D, GOSWAMI S K. Stator side active and reactive power control with improved rotor position and speed estimator of a grid connected DFIG (doubly-fed induction generator)[J]. Energy, 2015, 89: 461-472.

[4]FU H L, THIEN H T. Modeling a wind turbine system using DFIG and realization of current control on the model with fuzzy logic controller[M]//ZELINKA I, DUY V H, CHA J. AETA 2013: Recent Advances in Electrical Engineering and Related Sciences. Berlin Heidelberg, Germany: Springer, 2014: 85-92.

[5]卫志农, 俞小勇, 吴佳佳. 基于自抗扰控制的双馈发电机无速度传感器控制[J]. 电力自动化设备, 2011, 31(1): 15-18.

WEI Zhinong, YU Xiaoyong, WU Jiajia. Speed sensorless control of DFIG based on ADRC[J]. Electric Power Automation Equipment, 2011, 31(1): 15-18.

[6]BEKAKRA Y, ATTOUS D B. DFIG sliding mode control fed by back-to-back PWM converter with DC-link voltage control for variable speed wind turbine[J]. Frontiers in Energy, 2014, 8(3): 345-354.

[7]SUSPERREGUI A, JUGO J, LIZARRAGA I,etal. Automated control of doubly fed induction generator integrating sensorless parameter estimation and grid synchronisation[J]. IET Renewable Power Generation, 2014, 8(1): 76-89.

[8]PATTNAIK M, KASTHA D. Adaptive speed observer for a stand-alone doubly fed induction generator feeding nonlinear and unbalanced loads[J]. IEEE Transactions on Energy Conversion, 2012, 27(4): 1018-1026.

[9]BENBOUZID M, BELTRAN B, MANGEL H,etal. A high-order sliding mode observer for sensorless control of DFIG-based wind turbines[C]//Proceedings of the 38th Annual Conference on IEEE Industrial Electronics Society. Montreal, Canada: IEEE, 2012: 4288-4292.

[10]BEZZA M, MOUSSAOUI B E L, FAKKAR A. Sensorless MPPT fuzzy controller for DFIG wind turbine[J]. Energy Procedia, 2012, 18: 339-348.

[11]ZHANG Yang, WANG Zijing, BIE Zhaohong,etal. Studies on sensor-less hysteretic multi-scalar control of doubly fed machine for wind power generators[J]. Energy Procedia, 2011, 12: 741-751.

[12]贺益康, 胡家兵, 徐烈. 并网双馈异步风力发电机运行控制[M]. 北京: 中国电力出版社, 2012: 29-32.

[13]吴忠强, 马宝明, 庄述燕. 双馈风力发电系统终端滑模控制研究[J]. 电机与控制学报, 2012, 16(8): 94-100.

WU Zhongqiang, MA Baoming, ZHUANG Shuyan. Research on terminal sliding mode control for double-fed wind power system[J]. Electric Machines and Control, 2012, 16(8): 94-100.

[14]王晓雷, 毋炳鑫, 吴必瑞. 风力机的新型变桨距自抗扰控制系统[J]. 动力工程, 2009, 29(3): 250-253.

WANG Xiaolei, WU Bingxin, WU Birui. A new active disturbance rejection variable pitch control system of wind turbine[J]. Journal of Power Engineering, 2009, 29(3): 250-253.

[15]LIANG R H, WANG J C, CHEN Y T,etal. An enhanced firefly algorithm to multi-objective optimal active/reactive power dispatch with uncertainties consideration[J]. International Journal of Electrical Power & Energy Systems, 2015, 64: 1088-1097.

[16]GAO Mingliang, HE Xiaohai, LUO Daisheng,etal. Object tracking using firefly algorithm[J]. IET Computer Vision, 2013, 7(4): 227-237.

[17]王玺, 张学东, 司风琪, 等. 基于最小二乘支持向量机和萤火虫算法的开式循环水系统优化[J]. 动力工程学报, 2015, 35(3): 251-256.

WANG Xi, ZHANG Xuedong, SI Fengqi,etal. Open circulating water system optimization based on LSSVM and firefly algorithm[J]. Journal of Chinese Society of Power Engineering, 2015, 35(3): 251-256.

Terminal Sliding Mode Control Optimization for Maximal Wind Energy Capture of DFIG Without Speed Sensors

WUZhongqiang,WANGXinyi,ZHAOXibo

(Key Lab of Industrial Computer Control Engineering of Hebei Province, School of Electrical Engineering, Yanshan University, Qinhuangdao 066004, Hebei Province, China)

To achieve maximum wind energy capture of doubly-fed induction generators (DFIG), a Backstepping terminal sliding mode controller was designed for the complex nonlinear and strongly coupled system. The specific way is to solve the problem of large initial error by arranging the reference input signal using tracking-differentiator (TD), and then to realize speed sensorless operation using extended state observer (ESO) to estimate the flux linkage and motor speed, and reduce the ripples of flux linkage and torque, and finally to simplify the design of Backsteepping terminal sliding mode controller through observation and compensation on disturbing terms like coupling disturbance in current equations. Meanwhile, the firefly optimization algorithm (FA) is used to optimize those parameters to be set in the controller and observer. Results show that floating tracking can be achieved in the control system via the scheme, and the control accuracy is thus improved.

doubly-fed induction generator; maximal wind energy capture; Backstepping terminal sliding mode control; extended state observer; firefly algorithm

2015-09-16

2016-01-21

河北省自然科学基金资助项目(F2016203006)

吴忠强(1966-)，男，上海人，博士，教授，主要从事风力发电系统方面的控制研究.电话(Tel.):13833590482；

E-mail:mewzq@163.com.

1674-7607(2016)09-0716-10

TP273

A学科分类号：120.10