强声波在电站锅炉中传播特性的研究

姜根山，　许伟龙，　孔　倩，　安连锁

(1.华北电力大学 数理学院，河北保定 071003；2.华北电力大学 能源动力与机械工程学院，北京 102206)



强声波在电站锅炉中传播特性的研究

姜根山1，许伟龙2，孔倩1，安连锁2

(1.华北电力大学 数理学院，河北保定 071003；2.华北电力大学 能源动力与机械工程学院，北京 102206)

对位于可听声频率范围的强声波在电站锅炉中的传播特性进行了研究.基于简单波假设理论，对声压级达到160 dB的强声波传播过程中畸变和谐波生成的机理进行了分析研究，并计算了不同频率下声波的冲击波形成距离；计算得到炉内黏热流体介质中伯格斯方程的严格解，研究了发生非线性效应与耗散效应下强声波的传播特性；采用数值计算方法求解了弛豫流体介质中强声波传播的非线性波动方程，讨论了弛豫介质中声波的传播特性.结果表明：冲击波形成距离与声波频率成反比，随着声波频率的增大，非线性效应减弱，耗散效应增强.

强声波； 冲击波； 电站锅炉； 炉膛； 传播特性

对于电站锅炉，炉内“声波影响燃烧技术”、“声波清灰技术”、“换热器管道泄漏声学检测技术”以及“声学测温、测流技术”等，均为利用声学理论和技术来保障锅炉安全经济运行、提高燃烧和热量转换效率的重要技术手段[1-4].但是，支撑这些技术的炉内声学理论研究却长期处于落后水平，造成其基础理论研究严重滞后于其技术需求的局面，并最终成为阻碍这些技术进一步推广应用的瓶颈.

当声波声压级达到140 dB以上时，声压和质点速度的振幅相对于大气压强和声速来说已不能认为很小以致可以忽略不计，声波不再满足线性化条件[5]，此时称为强声波.强声波具有大振幅和高畸变性质，同时还具有辐射压力、声流和空化等多个次级效应，这些次级效应在声波与物质相互作用时往往能够起到特殊的效果[5-7].为了系统研究炉内声学效应，首先应研究强声波在炉内的传播特性.国内外学者对强声波的传播特性已经进行了大量研究[8].Lee等[9]提出了一种时域算法，研究了有限振幅声束在均匀的、热黏性流体中的传播特性，同时探讨了多弛豫介质中的声吸收和频散效应.Cleveland等[10-11]研究了在多弛豫介质中，几何膨胀、媒质不均匀性等对强声波传播的影响.Szabo等[12]引入一个相关联的卷积传播算子到三维波动方程中，将衰减以及频散效应直接包含在时域里，研究了声波在线性媒质中的线性或非线性传播特性.Purrington等[13]在此基础上，提出了时域传播因子，并根据它直接模拟相关联的传播特性.Norton等[14]将这种方法推广到二维各向异性的媒介，采用时域有限差分法得到的结果与数值分析解结果完全一致.

目前对强声波传播特性的研究大多是针对超声、液体组织以及固体中的研究，针对可听声频率范围内声波在空气中的传播特性的研究相对较少.笔者针对电站锅炉，研究了在炉内负压、高温、黏热和弛豫介质等条件下炉膛中强声波的传播特性，得出了强声波在炉内传播过程中形成冲击波的一般规律，为研究炉内强声波传播和声效应提供了可依据的声学参数.

1　冲击波的形成距离及波形畸变分析

笔者主要研究可听声频率范围(声波频率f=20～20 000 Hz)内的炉内强声波传播行为.根据冲击波理论，强声波在传播过程中波形会不断发生畸变，并最终形成陡峭的锯齿形间断波形，即冲击波.首先研究冲击波的形成距离与声波频率的关系.

1.1波形畸变及冲击波的形成距离

在一维、忽略流体质量力的情况下，理想流体介质的运动方程和连续性方程可以表示为

(1)

(2)

式中：ρ为介质密度，kg/m3；u为质点速度，m/s；p为流体介质的压力，Pa；t为时间，s；x为传播距离，m.

为了得到非线性方程组的严格解，引入所谓简单波假设，即

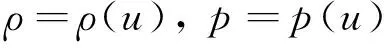
(3)

计算可得

(4)

式中：F为一任意函数；c为有限振幅声波在介质中的传播速度，m/s.

式(4)为非线性方程式(1)和式(2)在简单波假设下得到的严格解，即为黎曼-厄恩肖解[15].对于理想气体，根据绝热物态方程可知

(5)

式中：c0为小振幅声波在介质中的传播速度，m/s；γ为流体介质的比热容比；p0为平衡压力，Pa；ρ0为平衡密度，kg/m3.

联立式(4)和式(5)并取正向传播速度，可得

(6)

当初始扰动是角频率为ω的正弦扰动时，则t时刻在x点的质点振动速度为

(7)

式中：β为介质的非线性系数；u0为质点振动速度的幅值，m/s.

从式(7)可以看出，波形上各点相对于u=0点有一个传播速度差βu.随着传播距离的增大，非线性畸变不断积累并在传播距离上形成间断面.冲击波最初形成的空间位置x=Xs处的切线应为垂直线，即

(8)

由式(8)可得

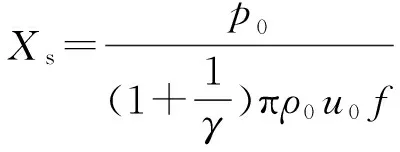
(9)

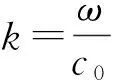
由式(9)可知，在其他条件相同的情况下，冲击波的形成距离与平衡压力成正比，与声波频率成反比，与流体介质的振动动量密度峰值成反比，并随着流体介质比热容比的增加，冲击波形成距离呈增大趋势.

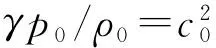
表1　烟气的热物理性质

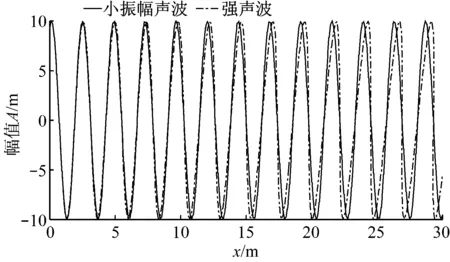
图1　简单波解描述的波形畸变及冲击波形成过程Fig.1　Wave distortion and shock wave formation described by simple wave solutions

由图1可以看出，随着传播距离的增大，波形畸变不断积累并于Xs处形成冲击波，由式(9)计算得到Xs=24.3 m.

通常国内600 MW超临界机组炉膛长21 882 mm、宽16 955 mm、高50 960 mm[16]，当炉内温度为1 200 ℃时，根据式(9)，在炉内形成冲击波的频率应大于151.2 Hz，炉内燃烧区域一般在炉膛中部，当一列强声波从锅炉不同壁面中心垂直射入，频率分别在704.48 Hz、913.07 Hz以及302.4 Hz左右时，能够在燃烧段形成冲击波，冲击波的形成对炉内燃烧会产生重要影响.通过计算可得，声压级为160 dB的强声波在不同频率下具有不同的冲击波形成距离，如在可听声频率20～20 000 Hz内，Xs在0.38～387.03 m之间.

1.2波形畸变分析

在马赫数Ma<<1的情况下，对式(7)中的1/(1+βu/c0)项作级数展开，并保留到一次项，利用冲击波形成距离Xs，则式(7)可表示为

(10)

其中，σ=x/Xs，τ=t-x/c0.

式中：σ为以冲击波形成距离为尺度的距离变量；τ为关于x和t的函数，为文中引入的新独立变量.

对式(10)进行傅里叶级数展开，得：

(11)

式中：Bn(σ)为傅里叶级数展开后n阶谐波的振幅.

(12)

(13)

式中：Jn(nσ)为n阶柱贝塞尔函数.

将式(13)代入式(11)，得：

(14)

图2所示为基波、二阶谐波(ω=4 000 Hz)和三阶谐波(ω=6 000 Hz)在ω=2 000 Hz、c0=757.37 m/s、β=1.18、u0=10 m/s时，随着传播距离增加而发生的变化.

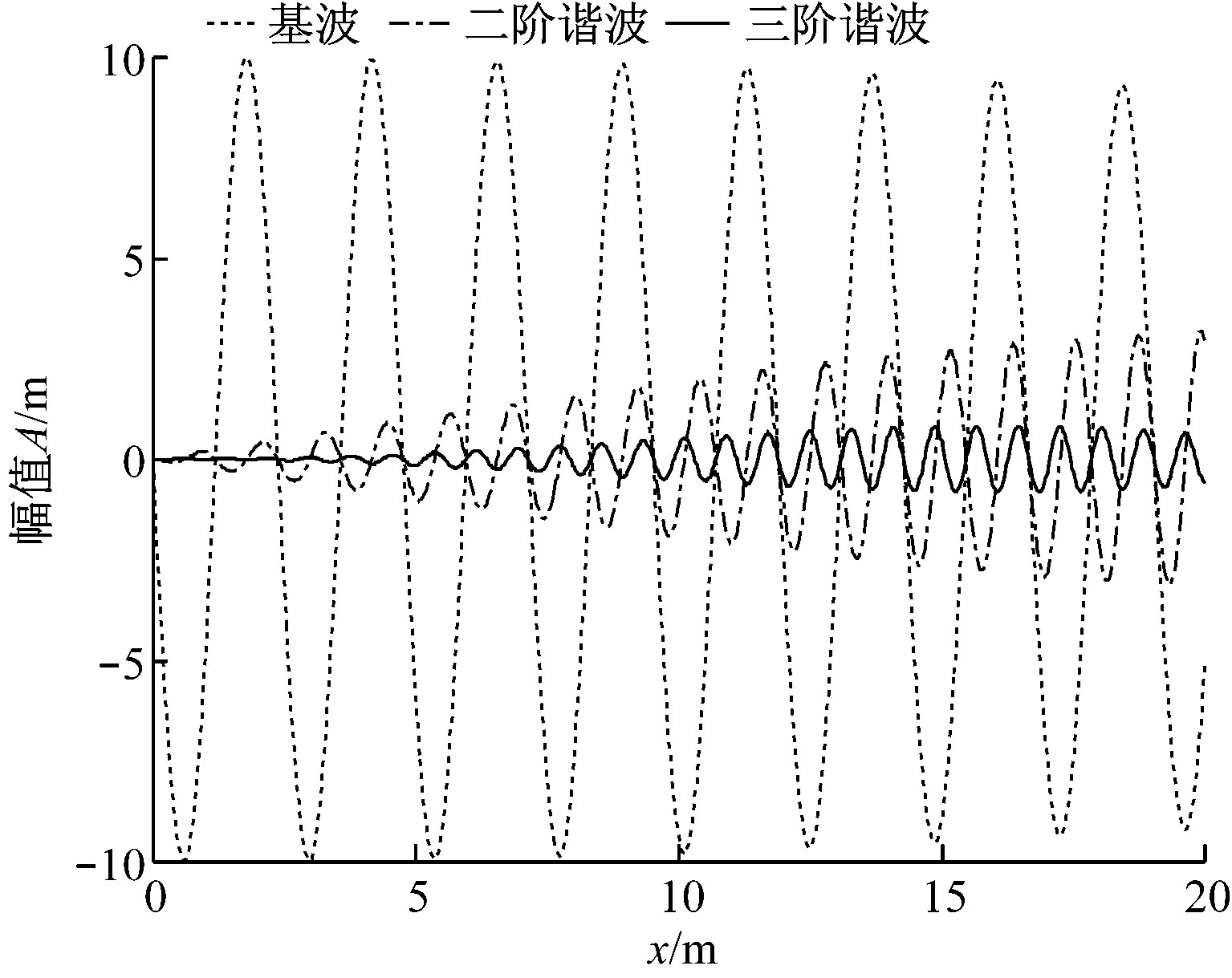
图2　基波、二阶谐波以及三阶谐波的变化情况

Fig.2Variation of fundamental, second-order harmonic and third-order harmonic wave with propagation distance

由图2可知，由于非线性效应，各阶谐波成分逐渐增大，而基波成分逐渐减小，即基波的能量逐渐减弱，各阶谐波的能量逐渐增强.因此，随着传播距离的增加，谐波可积累，最终可形成陡峭间断的冲击波.同时还可以发现，随着阶数的增加，谐波的振幅越来越小.

2　炉内介质的黏热性对强声波传播的影响

实际介质总是非理想的，当一列强声波在黏热流体介质中传播，暂不考虑流体介质的弛豫效应，流体介质的黏滞性和热传导性在声波传播过程中会吸收声波，使之衰减.为了便于讨论，假设炉膛为吸收边界.

黏热流体运动方程为

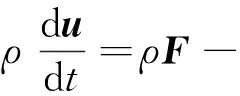
(15)

式中：▽为哈密尔顿算子;▽2为拉普拉斯算子，对于无旋运动，▽▽·u=▽2u；μ′为切变黏滞系数，kg/(m·s)；μ″为膨胀黏滞系数，kg/(m·s)；F为体积力，N.

连续性方程和经过热传导修正的物态方程为

(16)

其中，ρ′=ρ-ρ0.

(17)

式中：λ为导热系数，W/(m·K)；cv为质量定容热容，kJ/(kg·K).

式(15)～式(17)构成了黏热流体运动的方程组.假设流体做无旋运动，不考虑流体质量且在一维情况下，将方程组通过伴随坐标变换，在二级近似下即可化为著名的伯格斯方程：

(18)

其中，b=μ″+2μ′+λ(1/cv-1/cp).

声波沿正方向传播，有τ=t-x/c0.

为了得到伯格斯方程的严格解，先将式(18)无量纲化，在式(18)两端除以βMau0/xc，令V=u/u0，σ=βMax/xc，xc=c0/ω，Γ=2ρ0βMac0xc/b，y=c0τ/xc，则式(18)可简化为

(19)

利用Cole-Hopf变换，并经过一系列推算过程，得到伯格斯方程的精确解[18]：

(20)

式中：In(x)为虚宗量贝塞尔函数.

(21)

式中：α为黏滞及热传导耗散所引起的小振幅吸收系数.

因此，Γ可以用来衡量强声波在黏热介质传播过程中非线性效应与耗散效应的强弱.

取u0=10 m/s，在可听声频率下计算可得，当f=20 Hz时，Γ=1 000 Hz，此时非线性效应要远远强于耗散效应；当f=20 000 Hz时，Γ≈1，此时耗散效应强于非线性效应.

图3和图4给出了当Γ≈1时强声波的传播特性.由图3可知，随着σ的增大，强声波的振幅有明显的衰减；由图4也可以看出，在0<σ<1内，强声波不断衰减.但是图3和图4中几乎没有发现波的畸变，此时，强声波为典型的衰减波.

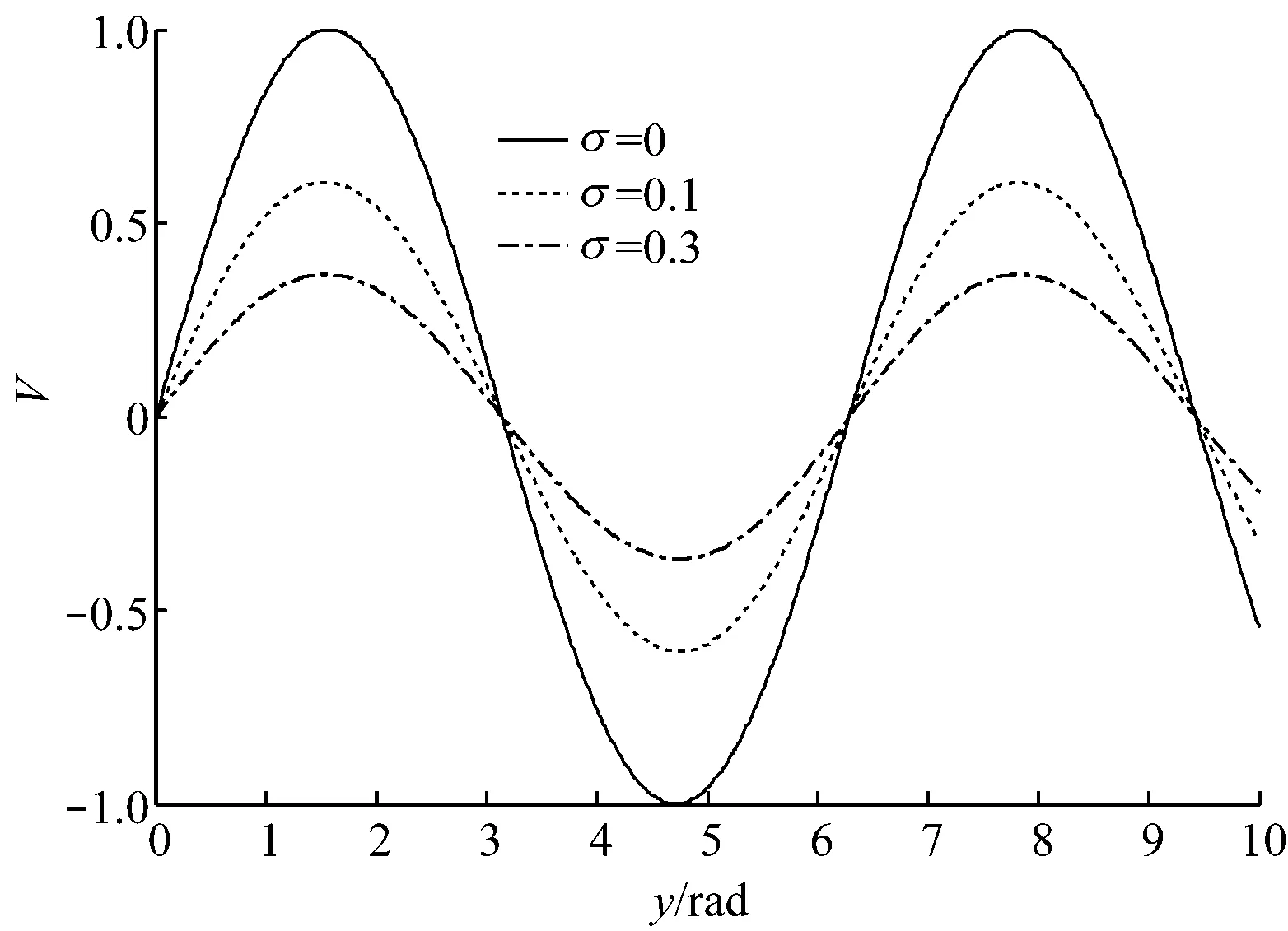
图3　Γ≈1、0<σ<1时，式(20)描述的衰减波Fig.3　Wave attenuation described by equation (20) for Γ≈1, 0<σ<1

图4　Γ≈1、0<σ<1时，式(20)描述的衰减波的三维图Fig.4　3D diagram of wave attenuation described by equation (20) for Γ≈1, 0<σ<1

在求解式(20)的过程中，为了更快地收敛，σ/Γ不宜取值太小.图5和图6给出了当Γ=10(此时非线性效应比耗散效应要强)时强声波的传播特性，此时f=2 000 Hz.由图5可以看出，随着σ的增大，波形开始畸变，同时伴随着衰减，当σ=1时，开始形成冲击波；当σ=π/2时，冲击波的幅度较σ=1时的幅度大；而当σ=5时，冲击波的幅度变小.结合图6可以明显看出，冲击波形成后会在某处达到最大幅度，之后慢慢衰减.

如图7和图8所示，当σ>>Γ时，式(20)的解V与初始强声波的振幅无关，波的振幅很小，此时处于声饱和状态.

图5　Γ=10、σ<Γ时，式(20)描述的波的畸变与冲击波形成过程

Fig.5Wave distortion and shock wave formation described by equation (20) forΓ=10,σ<Γ

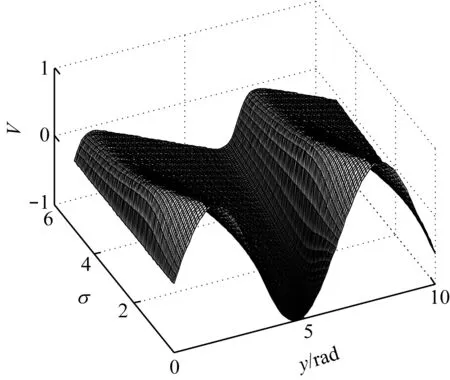
图6　Γ=10、σ<Γ时，式(20)描述的衰减波的三维图Fig.6　3D diagram of wave attenuation described by equation (20) for Γ=10, σ<Γ

图7　Γ=10、σ≫Γ时，式(20)所描述的波形Fig.7　Waveform described by equation (20) for Γ=10,σ≫Γ

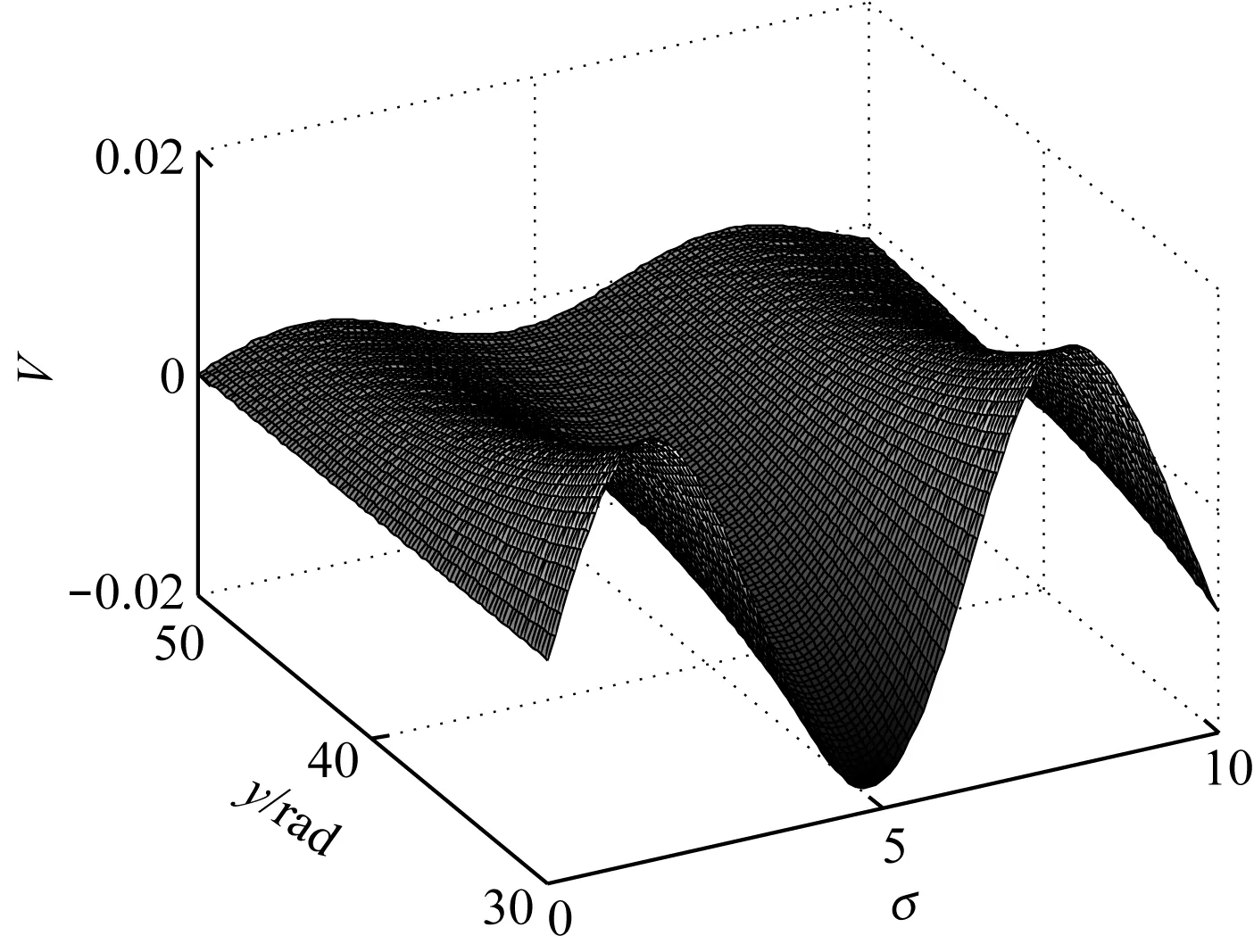
图8　Γ=10、σ≫Γ时，式(20)描述的波形的三维图Fig.8　3D diagram of waveform described by equation (20) for Γ=10, σ≫Γ

在黏热流体介质中，由于非线性作用和耗散作用的共同存在和相互平衡，强声波既有衰减又有畸变，这时不形成间断冲击波，而是形成一个连续变化的冲击波.当耗散效应很强、非线性效应很弱时，形成典型的衰减波；当耗散效应很弱、非线性效应很强时，可以忽略流体介质黏热的影响.强声波具有大振幅，可以应用于声波吹灰.强声波的非线性效应包括辐射压力、声流和空化等多个次级效应，这些次级效应在炉膛中可以强化煤粉燃烧以及炉管换热等.因此，将强声波应用于电站炉膛时，应尽量避免强声波过快衰减且充分利用强声波的非线性效应；若选取频率较高的强声波，在传播过程中，强声波有着明显的衰减而非线性效应很弱，因此应该选取较低频段的强声波.

3　炉内介质的弛豫效应对强声波传播的影响

在气体和液体的大量实验研究中，学者们发现声速有随频率的增加而显著增大的现象，这种声速随频率变化的现象称为频散或色散[19].引起频散效应的原因有2种：(1)弛豫吸收引起的频散现象；(2)边界效应引起的频散现象.笔者仅讨论第1种情况.

之前讨论黏热介质时并没有考虑频散效应.为了研究弛豫介质的影响，本节忽略黏滞热传导损失，则在一维、忽略流体质量力的情况下，运动方程和连续性方程如式(1)和式(2)所示.

既包括非线性效应又包括弛豫效应的物态方程如下：

(22)

p′=p-p0

式中：τr为弛豫时间，s；Ci为流体介质初始平衡态时(ωτr→0)的声速，m/s；C∞为流体介质达到新的平衡态后(ωτr→∞)的声速，m/s；ξ0表示介质达到的新的平衡态.

应用与第2节相同方法，对方程进行伴随坐标变换，并将方程无量纲化，令ζ=ωτ，σ=βkMax，V=u/u0，得

(23)

D=m/2βMa

式(22)即为描述弛豫流体介质中强声波传播的非线性波动方程.方程右端第1项是由弛豫吸收引起的，第2项是频散的贡献.式(22)的求解是很困难的，笔者采用有限差分法对该式进行数值求解，进而研究弛豫流体介质中强声波的传播特性；利用二阶精度的有限差分格式，并以V(t,0)=sin(ωt)为输入波形.在电站锅炉中，流体介质中弛豫时间量级小于10-5s，对于可听声，有ωτr<1.由于20～20 000 Hz内声速几乎保持为一常数[19]，因此D<<1，此时非线性效应远强于弛豫效应，取D=0.005、Δσ=0.001、Δζ=0.1、ωτr=1时，对式(22)进行数值求解，可得图9所示的弛豫流体介质中强声波的传播特性.

由图9可知，初始输入的正弦波在弛豫流体介质中传播时波形发生了变化，主要为波形逐渐变陡峭并出现多值，最终形成间断冲击波；同时，原来对称的波形慢慢变为不对称，即形成非对称波形.当σ=1时，形成了冲击波，且弛豫流体介质的弛豫吸收出现弛豫峰，这时的弛豫吸收最大，频散也最强.

然而在电站锅炉中，可听声频率的声波在传播过程中的弛豫效应与第2节讨论的耗散效应相比几乎可以忽略不计.另外，值得指出的是，强声波在炉内传播过程中还受到固体粉尘等颗粒物的影响，关于这部分内容的研究结果笔者另文报道.

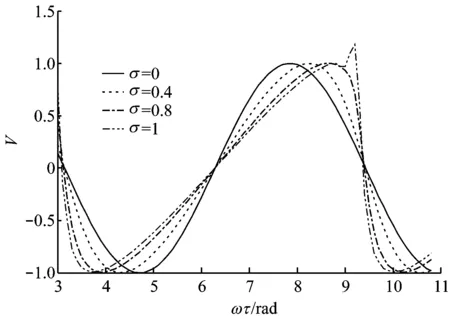
图9　弛豫流体介质中强声波的传播特性Fig.9　Propagation characteristics of high-intensity sound in relaxation fluid

4　结　论

(1)冲击波的形成距离随着频率的增加而减小，通过得到的冲击波形成距离的关系式，依据电站锅炉大小可以选择合适的声波频段.

(2)炉内介质的黏热性使得强声波在传播过程中波形既有衰减又有畸变，形成一个连续变化的冲击波.在较低的频段下，声波在传播过程中的非线性效应十分明显，声波衰减并不剧烈，且作用距离更长；随着声波频率的增大，耗散效应逐渐增强以至大于非线性效应，声波衰减随着频率的增加而增强.

(3)炉内介质的弛豫效应使得强声波在传播过程中波形逐渐变陡峭并出现多值，最终形成间断冲击波；同时原来对称的波形慢慢变为不对称.但在可听声频率范围内，弛豫效应作用并不明显.

[1]姜根山, 朱永波, 田静, 等. 锅炉声波除灰的声学分析[J]. 工程热物理学报, 2001, 22(6): 687-690.

JIANG Genshan, ZHU Yongbo, TIAN Jing,etal. Acoustic analysis for the sonic soot cleaning in boilers[J]. Journal of Engineering Thermophysics, 2001, 22(6): 687-690.

[2]姜根山, 安连锁, 杨昆. 锅炉换热器管道泄漏口声辐射指向性特征数值研究[J]. 中国电机工程学报, 2002, 22(6): 126-131.

JIANG Genshan, AN Liansuo, YANG Kun. Numerical study of directionality patterns for acoustic radiation from a leak source on a heat-exchanger cylinder in boilers[J]. Proceedings of the CSEE, 2002, 22(6): 126-131.

[3]沈国清, 安连锁, 姜根山, 等. 基于声学CT重建炉膛二维温度场的仿真研究[J]. 中国电机工程学报, 2007, 27(2): 11-14.

SHEN Guoqing, AN Liansuo, JIANG Genshan,etal. Simulation of two-dimensional temperature field in furnace based on acoustic computer tomography[J]. Proceedings of the CSEE, 2007, 27(2): 11-14.

[4]安连锁, 王鹏, 姜根山, 等. 锅炉承压管泄漏声传播时间延迟估计[J]. 中国电机工程学报, 2012, 32(2): 16-23.

AN Liansuo, WANG Peng, JIANG Genshan,etal. Time delay estimation for boiler tube leak sound propagation[J]. Proceedings of the CSEE, 2012, 32(2): 16-23.

[5]钱祖文. 我国非线性声学方面的研究进展[J]. 物理, 1999, 28(10): 593-600.

QIAN Zuwen. Nonlinear acoustics in China[J]. Physics, 1999, 28(10): 593-600.

[6]VALVERDE J M. Acoustic streaming in gas-fluidized beds of small particles[J]. Soft Matter, 2013, 9(37): 8792-8814.

[7]AMIRI S, TAHER R, MONGEAU L G. Experimental study of the oscillatory velocity and temperature near a heated circular cylinder in an acoustic standing wave[J]. International Journal of Heat and Mass Transfer, 2014, 69: 464-472.

[8]HAMILTON M F, BLACKSTOCK D T. Nonlinear acoustics[M]. San Diego, USA: Academic Press, 1998.

[9]LEE Y S, HAMILTON M F. Time-domain modeling of pulsed finite-amplitude sound beams[J]. Journal of the Acoustical Society of America, 1995, 97(2): 906-917.

[10]CLEVELAND R O. Effects of atmospheric stratification on sonic-boom propagation [J]. The Journal of the Acoustical Society of America, 1995, 97(5): 3257.

[11]CLEVELAND R O, HAMILTON M F, BLACKSTOCK D T. Time-domain modeling of finite-amplitude sound in relaxing fluids[J]. The Journal of the Acoustical Society of America, 1996, 99(6): 3312-3318.

[12]SZABO T L, WU Junru. A model for longitudinal and shear wave propagation in viscoelastic media[J]. The Journal of the Acoustical Society of America, 2000, 107(5): 2437-2446.

[13]PURRINGTON R D, NORTON G V. A numerical comparison of the Westervelt equation with viscous attenuation and a causal propagation operator[J]. Mathematics and Computers in Simulation, 2012, 82(7): 1287-1297.

[14]NORTON G V, NOVARINI J C. Including dispersion and attenuation in time domain modeling of pulse propagation in spatially-varying media[J]. Journal of Computational Acoustics, 2004, 12(4): 501-519.

[15]BEYER R T. Nonlinear acoustics in fluids[M]. New York, USA: Van Nostrand Reinhold Co., 1984.

[16]周星龙, 程乐鸣, 夏云飞, 等. 600 MW循环流化床锅炉水冷壁和中隔墙传热特性[J]. 中国电机工程学报, 2014, 34(2): 225-230.

ZHOU Xinglong, CHENG Leming, XIA Yunfei,etal. Heat transfer characteristic of water wall and partition wall in a 600 MW CFB boiler[J]. Proceedings of the CSEE, 2014, 34(2): 225-230.

[17]FUBINI-GHIRON E. Anomalie nella propagazione di onde acustiche di grande ampiezza[J]. Alta Frequenza, 1935, 4: 530-581.

[18]那仁满都拉. 流体与固体介质中有限振幅波、孤立波的传播和相互作用的理论与求解方法研究[D]. 长春: 吉林大学, 2005.

[19]杜功焕, 朱哲明, 龚秀芬. 声学基础[M]. 2版.南京: 南京大学出版社, 2001.

Propagation Characteristics of High-intensity Sound in Power Plant Boilers

JIANGGenshan1,XUWeilong2,KONGQian1,ANLiansuo2

(1. School of Mathematics and Physics, North China Electric Power University, Baoding 071003,Hebei Province, China; 2. School of Energy, Power and Mechanical Engineering,North China Electric Power University, Beijing 102206, China)

Propagation characteristics of high-intensity sound with audio frequencies in power plant boilers were studied. Firstly, the mechanism of distortion and harmonic generation occurring in propagation process of high-intensity sound with pressure level of 160 dB was analyzed based on the hypothesis of simple wave theory, while the formation distance of shock waves was calculated for high-intensity sounds of different frequencies. Secondly, the strict solution of burgers equation for viscous fluid in the furnace was calculated, and the propagation characteristics of high-intensity sound were analyzed under the circumstance of nonlinear effect and dissipation effect. Finally, the propagation characteristics of high-intensity sound in the relaxation medium were discussed after solving relevant nonlinear wave equations by numerical methods. Results show that the formation distance of shock waves is inversely proportional to the sound frequency; the nonlinear effect weakens while the dissipation effect improves with the rise of sound frequency.

high-intensity sound; shock wave; power plant boiler; furnace; propagation characteristic

2015-10-14

2015-12-28

国家自然科学基金资助项目(11474091,11274111)；河北省自然科学基金资助项目(A2015502077)；中央高校基本科研业务费专项资金资助项目(2015XS105)

姜根山(1963-)，男，河北邢台人，教授，博士生导师，研究方向为炉内声学理论及应用研究.

许伟龙(通信作者)，男，博士研究生，电话(Tel.): 15632248235；E-mail：xuweilong@ncepu.edu.cn.

1674-7607(2016)09-0683-07

TK224

A学科分类号：470.10