带有双时滞的SEIRVS模型的数学分析
2016-10-11 06:39:47黄新峰乔志琴
高师理科学刊 2016年2期
黄新峰[1],乔志琴
带有双时滞的SEIRVS模型的数学分析
黄新峰[1],乔志琴
(中北大学 理学院,山西 太原 030051)
在已有的双时滞SEIRS模型基础上考虑对易感者进行接种免疫,分析所给出的模型无病平衡点的局部稳定性,以及地方病平衡点的存在性及其相应的个数,得到了在某些特殊情况下的地方病的稳定性.
双时滞;SEIRVS模型;稳定性
传染病对人类的生存有着非常重要的影响[1],随着国际上传染病动力学的进一步研究[2],一些生物学因素被考虑到了传染病模型中,如将出生率和死亡率考虑到了传染病模型中,引入人口的年龄结构等.随着时滞微分方程理论[3]研究逐渐成熟,为了更加充分地反映传染病的传播特性,一些带有时滞的模型[4-7]被建立.文献[8]建立了一类含有2个时滞的SEIRS模型,该模型只考虑了疾病的潜伏期和恢复期,没有考虑对疾病进行接种免疫,由于这个模型含有2个时滞,研究地方病平衡点变得比较困难,只进行了地方病平衡点的局部研究,没有进行全局研究.本文在文献[8]的基础上,考虑对易感人群进行接种免疫,即在原SEIRS模型中引入了一类经过免疫的种群.假设接种率为,免疫失效率为,.
1模型建立
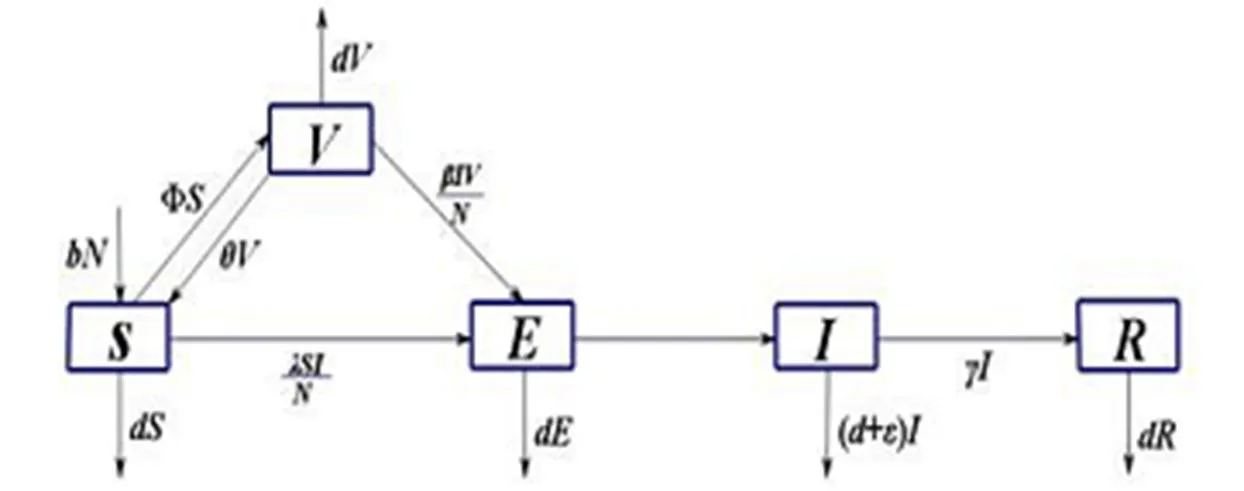
图1 含免疫期的仓室图
相应的数学模型为
进而有
采用文献[8]中方法,可以证明:满足系统(1)的解一定满足系统(2);相反,系统(2)满足初始条件的解也是系统(1)的解.当时,系统(1)存在唯一解,且.
2无病平衡点分析

即
3地方病平衡点分析
综上可知,结论成立.证毕.
猜你喜欢
Acta Mathematica Scientia(English Series)(2022年3期)2022-06-25 02:13:24
Chinese Physics B(2022年2期)2022-02-24 09:37:44
考试与评价·七年级版(2021年4期)2021-08-14 10:45:54
数学物理学报(2020年5期)2020-11-26 06:06:48
烟台果树(2019年1期)2019-01-28 09:34:58
传媒评论(2018年7期)2018-09-18 03:45:52
唐山文学(2016年12期)2016-03-01 05:24:32
IT时代周刊(2015年7期)2015-11-11 05:49:56
四川师范大学学报(自然科学版)(2015年2期)2015-02-28 14:07:40
应用数学与计算数学学报(2014年3期)2014-09-26 12:03:52

