BOUNDS FOR MULTILINEAR OPERATORS UNDER AN INTEGRAL TYPE CONDITION ON MORREY SPACES*

Qianjun HE (何骞君)

School of Applied Science，Beijing Information Science and Technology University，Beijing 100192，China

E-mail:heqianjun16@mails.ucas.ac.cn

Xinfeng WU (吴新峰)†

Department of Mathematics，China University Mining&Technology (Beijing)，Beijing 100083，China

E-mail:wuxf@cumtb.edu.cn

Dunyan YAN (燕敦验)

School of Mathematical Sciences，University of Chinese Academy of Sciences，Beijing 100049，China

E-mail:ydunyan@ucas.ac.cn

Abstract In this paper，we study a boundedness property of the Adams type for multilinear fractional integral operators with the multilinear Lr′，α-Hrmander condition and their commutators with vector valued BMO functions on a Morrey space and a predual Morrey space.Moreover，we give an endpoint estimate for multilinear fractional integral operators.As an application，we obtain the boundedness of multilinear Fourier multipliers with limited Sobolev regularity on a Morrey space.

Key words Multilinear fractional integral;Lr′，α-Hrmander condition;commutators;BMO spaces;Morrey spaces;multilinear Fourier multiplier

1 Introduction

It is well-known that the Morrey spaceLp，λ(Rn)(see the definition below)，introduced by Morrey in 1938，is connected to certain problems in elliptic PDE[39].After their inception it was found that Morrey spaces have many important applications to the Navier-Stokes equations (see[34，37，48])，the Schrdinger equations (see[42–45])，elliptic equations with discontinuous coefficients (see[8，10，13，14，26，41]) and to potential analysis (see[1，3]).The Morrey space associated with a heat kernel was studied in[12，20，52].Recently，in[4，6]，the authors set up several functional analyses and a potential theory for the Morrey space in harmonic analysis.

For 0＜p＜∞and 0＜λ≤n，the Morrey spaceLp，λ(Rn)(Lp，λfor short) is defined by the (quasi-) norm

where the supremum is taken over all cubesQ⊂Rnwith sides parallel to the coordinate axes and where|Q|denotes the volume ofQ.The Morrey space is Banach if 1≤p＜∞，and is quasi-Banach if 0＜p＜1.Ifλ=n，the Morrey spaceLp，n(Rn) coincides with the spaceLp(Rn) with equality of (quasi-) norms.

In 1975，Adams[1]first studied the boundedness of the Riesz potential in Morrey space.In 1987，Chiarenza and Frasca[9]proved the Morrey space boundedness of the Hardy-Littlewood maximal operator，the Riesz potential and singular integral operators.In 1993，Nakai[40]studied the bounds of the above operators in generalized Morrey space.In 1997，Ding[16]gave a characterization of the boundedness of the commutators of singular integral operators and a Riesz potential in generalized Morrey space.

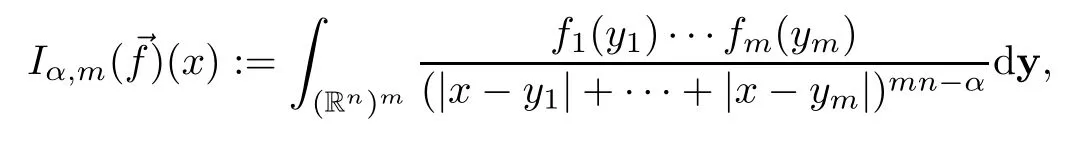
For 0＜α＜mn，x∈Rn，m∈N，the multilinear fractional integral operator=(f1，...，fm) was introduced by Kenig-Stein[35]，and the bounds on products of Lebesgue spaces were established.Recently，the bounds for multilinear operators in Morrey space have been investigated by many authors.Tang studied，in[47]，the boundedness ofIα，mon products of Morrey space.Wang，Jiang and Li[51]studied the boundedness of multilinear Fourier multipliers with limited Sobolev regularity in the Morrey space in the Banach space setting (p＞1)，but they left open the quasi-Banachcase 1/2＜p＜1.Ding and Mei established，in[17]，theLp1，λ1×Lp2，λ2→Lp，λboundedness and compactness for commutators of bilinear Calder´on-Zygmund operators and bilinear fractional integrals with BMO functions in the Banach space setting.Note that the kernel of bilinear Fourier multipliersTαmay not have the pointwise size and smoothness conditions，so that their bounds on Morrey space cannot be covered by the results in[17].

Bui and Duong[7]introduced and studied multilinear singular integral operators with certain integral conditions，which include the multilinear Fourier multipliers with limited smoothness.Chaffee-Torres and the second author[11]further introduced multilinear operators with kernels satisfying a new integral type condition，which is simpler and more general，but still covers the multilinear Fourier multipliers with limited smoothness.It would be interesting to establish the Morrey space boundedness for such a class of multilinear operators and their commutators，especially in the quasi-Banach setting 0＜p＜1.

In this paper，we consider the boundedness of multilinear singular integrals under integral type conditions in Morrey space.For 0＜α＜mn，the multilinear operatorsTαare initially defined on them-fold product of Schwartz spaces and by taking values into the space of tempered distributions

Assume that for a certain kernel functionK，

as an absolutely convergent integral wheneversuppfi.The kernel functionKof the operatorTαsatisfies the multilinearLr′，α-Hrmander condition:for 1＜r＜∞，

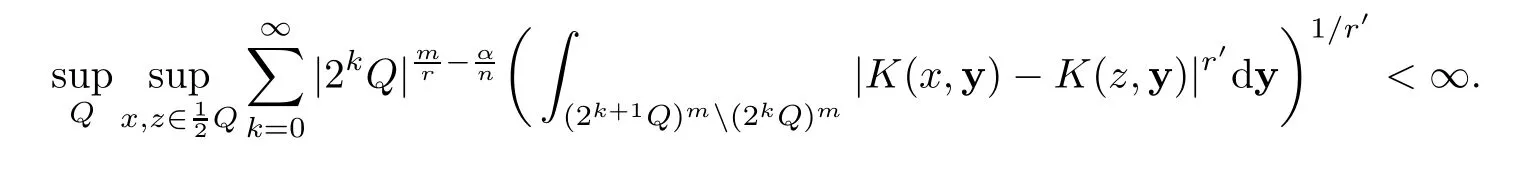
Forr=1，the above condition is understood as

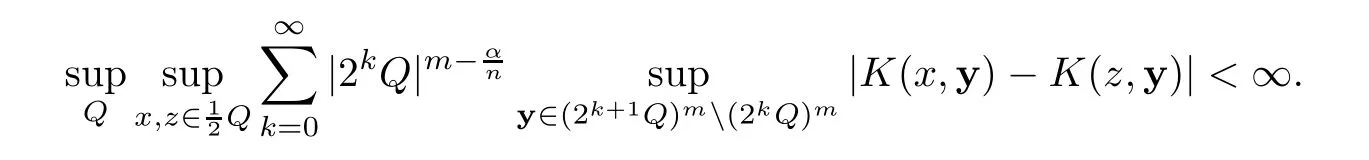
Our first main result can be stated as follows:

Theorem 1.1Let 0＜λ≤n，0≤α＜mn，0＜p≤q＜∞，1＜p1，...，pm≤∞ with 1/p=1/p1+···+1/pm.Suppose that→f=(f1，...，fm) is a collection ofmlocally integrable functions on Rn，1/q=1/p-α/λ，1≤r＜min (p1，...，pm，mn/α，mp) and 1/r*=m/r-α/n.If we have

which satisfies the multilinearLr′，α-Hrmander condition，then there exists a constantC＞0 such that

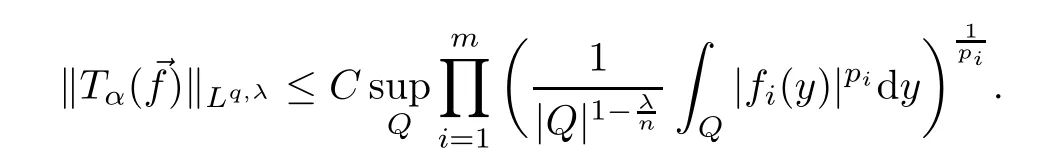
Remark 1.2The right hand side of the above inequality is called a multi-Morrey norm of f=(f1，f2，...，fm);this was introduced by Iida-Sato-Sawano-Tanakain[31].The multi-Morrey norm of f is smaller than the product ofmMorrey norms:

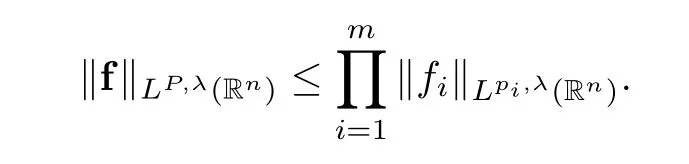
The authors of[31]proved similar results for the multilinear fractional integralsIm，αwith smooth kernels.Ifα＞0，our result in Theorem 1.1 covers the corresponding result in[31].

We shall now present a variant of Theorem 1.1.

Theorem 1.3Let 0＜λ≤n，0≤α＜mn，and letkbe an integer with 1≤k＜m，1＜p1，...，pk≤∞，0＜p＜q＜∞with 1/p=1/p1+···+1/pk.Decomposeα=α1+α2withα1＞0 andα2≥0.Suppose thatis a collection ofmlocally integrable functions on Rnand 1/q=1/p-α1/λ.IfTαsatisfies two conditions in Theorem 1.1，then there exists a constantC＞0 such that

Adams and Xiao[5]provided a new proof of the boundedness of the classical commutator[b，Iα]on Morrey spacesLp，λ，p＞1，and introduced a new formulation of the predual to a Morrey space withλ∈(0，n);namely，

Moreover，Adams and Xiao also obtained the boundedness of commutator[b，Iα]on aHp，λspace.In the above and below，for 0＜λ＜n，the symbolis the Hansdorffcapacity of ordern-λ，as a set function on Rn.

Our next result extends the result of Adams-Xiao in[5]to the multilinear setting.

Theorem 1.4Under the hypotheses of Theorem 1.1，if we have，in addition，that 1＜r＜q，then there exists a constantC＞0 such that，forj=1，...，m，

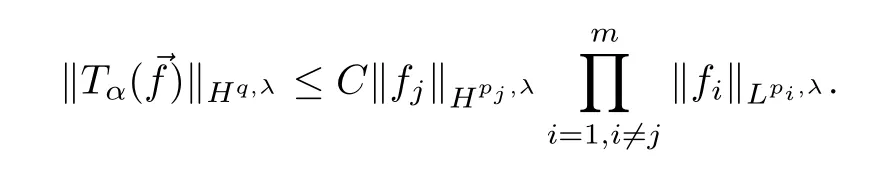
The following result provides an endpoint estimate forTα:

Theorem 1.5Let 0＜λ≤n，1＜p1，...，pm＜∞，1/p=1/p1+···+1/pm，1/p=α/λ，1≤r＜min (p1，...，pm，mn/α，mp)，nmax (m/r-1，0)＜α＜mnand 1/r*=m/r-α/n.IfTαsatisfies two conditions in Theorem 1.1，then

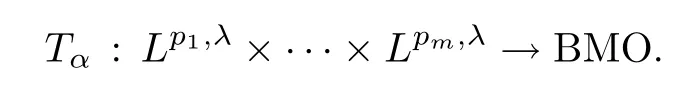
Remark 1.6The multlinear fractional integral operatorsIα，msatisfy the assumptions of Theorem 1.1 withr=1，and thus Theorem 1.5 covers the endpoint estimates obtained in[47，Theorem 1.1].Our result，however，is more general，and it can be applied to multilinear fractional Fourier multipliers with limited Sobolev regularity.

As a corollary，we obtain Moser-Trudinger type inequality，which extends a result of Adams and Xiao[3]to the multilinear case.The original Moser-Trudinger inequality was established by Trudinger[49]，Strichartz[46]，Moser[38]，and Adams[2]，and it plays an important role in the study of PDEs.

Corollary 1.7Let 0＜λ≤n，0＜q≤1，1＜p1，...，pm＜∞，p=λ/αand 1/p=1/p1+···+1/pm.IfTαsatisfies two conditions in Theorem 1.1 andnmax (m/r-1，0)＜α＜mn，then there exists a constantc＞0 such that

Now let us consider the commutator of a multilinear operator with a vector-valued BMO function.Recall that a locally integrable functionbis in BMO (Rn) if

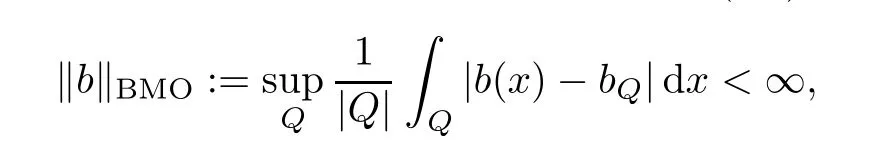
wherebQdenotes the average ofboverQ⊂Rn.Given a locally integrable vector function=(b1，...，bm)，define them-linear commutator of am-linear operatorTαwithby

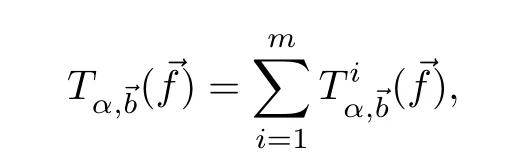
Theorem 1.8Under the hypotheses of Theorem 1.1，if we have，in addition，that∈BMOm，then there exists a constantC＞0 such that

Theorem 1.9Under the hypotheses of Theorem 1.3，if we have，in addition，that∈BMOm，then there exists a constantC＞0 such that

Theorem 1.10Under the hypotheses of Theorem 1.1，if we have，in addition，that 1＜r＜qand∈BMOm，then there exists a constantC＞0 such that，forj=1，...，m，

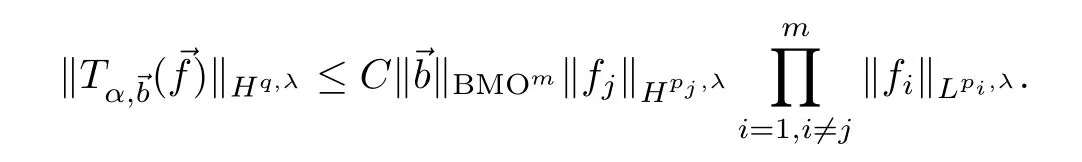
Theorem 1.11Let 0＜λ≤n，1＜p1，...，pm＜∞，1/p=1/p1+···+1/pm，1/p=α/λ，1≤r＜min (p1，...，pm，mn/α，mp)，nmax (m/r-1，0)＜α＜mnand 1/r*=m/r-α/n.IfTαsatisfies two conditions in Theorem 1.1 and→b∈BMOm，then

Corollary 1.12Let 0＜λ≤n，0＜q≤1，1＜p1，...，pm＜∞，p=λ/α，1/p=1/p1+···+1/pmand∈BMOm.IfTαsatifies two conditions in Theorem 1.1 andnmax (m/r-1，0)＜α＜mn，then there exists a constantc＞0 such that

Corollary 1.13Let 0＜λ≤n，=(f1，...，fm) be vector valued locally integrable functions on Rn，1＜p1，...，pm＜∞，1/p=1/p1+···+1/pmandp=λ/α＞1.Letfj∈Lpj，λbe supported inB(0，1) with ‖fj‖Lpj，λ≤1，and letbj∈L∞(j=1，...，m) with

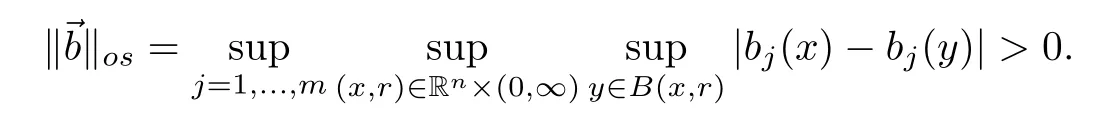
Ifnmax (m/r-1，0)＜α＜mnand 0＜q≤1，then

wherecis a non-negative constant.

The rest of the present paper is organized as follows:in Section 2，we will give some definitions and lemmas.The proof of Theorems 1.1，1.4，1.8 and 1.10 are presented in Section 3.In Section 4，we will give the proof of Theorems 1.5 and 1.11.A tacit understanding in the present paper is that all cubes in Rnare assumed to have their sides parallel to the coordinate axes，and we useℓ(Q) to denote the side-length ofQ.ForQ∈Rn，we usecQto denote the cube with the same center asQ，but with side-lengthcℓ(Q).We denote by|E|the Lebesgue measure ofE⊂Rn.ByA≾Bwe mean thatA≤cBwith some positive constantcindependent of the appropriate quantities.The positive constantCvaries from one occurrence to another.For a real numberp，1＜p＜∞，p′is the conjugate number ofp;that is，1/p+1/p′=1.

2 Preliminary Definitions and Lemmas

To prove our main results，we need the following definitions and lemmas:

Definition 2.1For any，the Hardy-Littlewood maximal function and sharp maximal function are defined by

Forδ＞0，we also define

The space of bounded mean oscillation (BMO) consists of all locally integrable functionsfwith

The next inequality is due to[15]，and it can be viewed as a variant of the Fefferman-Stein inequality in Morrey space.The original result in[15]was stated under the restriction 1＜p＜∞，but their proof actually works for all 0＜p＜∞.

Lemma 2.2([15]) If 0＜p，δ＜∞and 0＜λ＜n，then there exists a constantC＞0 such that

In the sequel，we will use the following simple Kolmogorov inequality[18]:

Lemma 2.3Letting 0＜p＜q＜∞，there is a constantC=Cp，qsuch that，for any measurable functionfand any cubeQ∈Rn，

Lemma 2.4([6]) Let 1＜p＜∞，and 0＜λ＜n.Then

where the supremum is over allg∈Hp′，λsuch that ‖g‖Hp′，λ≤1.

Lemma 2.5([5]) Ifw∈A1，then there exists aδ＞0 such thatwt∈A1whenever 0＜t＜1+δ.In particular，this holds for alltclose to 1.Moreover，ifc1denotes the“A1constant forw”，i.e.，

then，withctthe“A1constant forwt”，we have

wherecRHstands for the reverse Hlder constant.

Letting 0＜α＜mnand=(f1，···，fm) be a collection ofmlocally integrable functions on Rn，the multi-(sub) linear fractional maximal operatoris defined by

By the definition of Mα，it is easy to see that

Anm-linear operatorT:S (Rn)×···×S (Rn)→S′(Rn) hasmformal transposes.Thej-th transposeT*jofTis defined as the unique operator that satisfies the identity

for allf1，...，fm，h∈S (Rn).

For a vector→f=(f1，...，fm) of locally integrable functions and 0≤α＜mnand 1≤s＜define

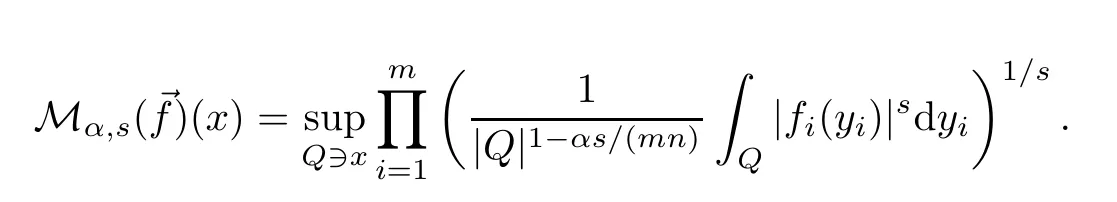
The advantage of multi-Morrey norms is that they can control this multilinear maximal operator.

Lemma 2.6([29]) Let 0＜λ≤n，0≤α＜mn，0＜s＜min (p1，...，pm)≤∞，0＜p＜∞，1/p=1/p1+···+1/pmand 0＜q＜∞with 1/q=1/p-α/λ.Then there exists some constantC＞0 such that

The following pointwise estimate was proven in[11]:

Lemma 2.7LetTαsatisfy the hypothesis of Theorem 1.1.If 0＜δ＜min (1，)，then there exists some constantC＞0 such that，for allfi∈Lpiwithr＜pi＜∞(i=1，...，m)，

We also need the following estimate，which can be viewed as an“off-diagonal”variant of Lemma 2.7:

Lemma 2.8Let 0＜λ≤n，0＜q＜∞，0＜p＜∞and 0＜α＜mn.Decomposeα=α1+α2withα1＞0 andα2≥0.Assume thatTαsatisfies the hypothesis of Theorem 1.1 and 1/q=1/p-α1/λ.Then

ProofIfλ=n，the Morrey spaceLp，λcoincides withLpwith comparable norms，and so the desired result follows directly from Lemma 2.7.

Now let us assume that 0＜α＜n.We shall borrow some ideas from[11]and[29]to prove the desired estimate.We may assume that the right hand side is finite.Without loss of generality we may assume thatf1，...，fmare nonnegative and that

Let 0＜δ＜min (1，)，and letQbe a cube in Rnthat containsx.It suffices to prove that

for some constantcQ，where the implicit constant is independent ofQ.In fact，once (2.5) is established，we take the supremum overQ⊂Rnto get

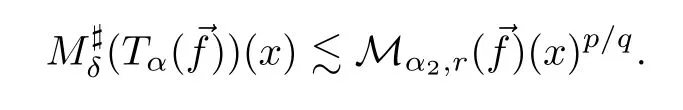
This，together with Lemma 2.2，yields that

which concludes the proof.

Let us now prove (2.5).DenoteIn the proof of Lemma 4.1 in[11]，it was shown that，for an appropriate constantcQ，

By the multilinearLr′，α-Hrmander condition ofK，we see that the right-hand side is majorized by

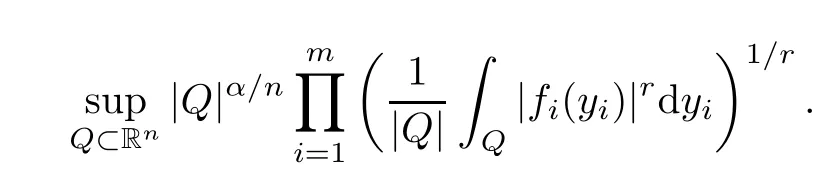
It thus remains to prove that，for anyQ∈Rnandx∈Q，

Denote

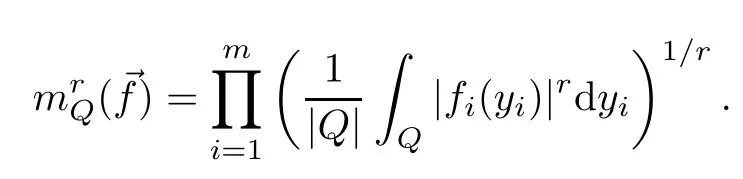
Notice that，forx∈Q，

It follows that

establishing (2.6). □

The following lemma is the key to our main results:

Lemma 2.9LetTαsatisfy the hypothesis of Theorem 1.1.If∈BMOm，0＜δ＜∈＜min (1) and=(f1，...，fm) are a collection ofmlocally integrable functions on Rn，then there exists some constantC＞0 such that，for anys＞rand for allfi∈Lpi(i=1，...，m) with

ProofBy linearity，it suffices to consider the case of=(b，0，...，0)∈BMOm.Fixb∈BMO and consider the operator

Fixx∈Rn.For any cubeQcentered atx，setThen we have

It suffices to show that

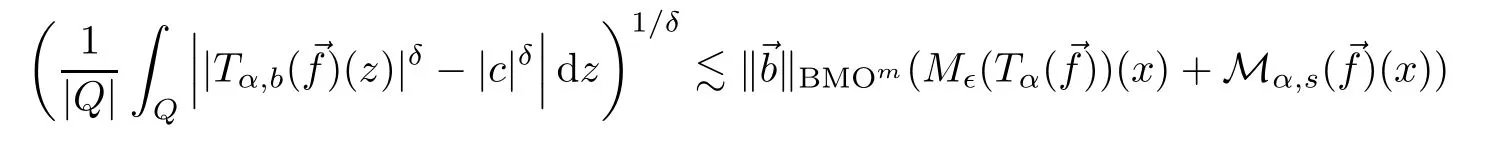
for somec.Since 0＜δ＜1，we have

ForP1，choosing 1＜t＜∈/δand applying the Hlder and John-Nirenberg inequalities，we get that

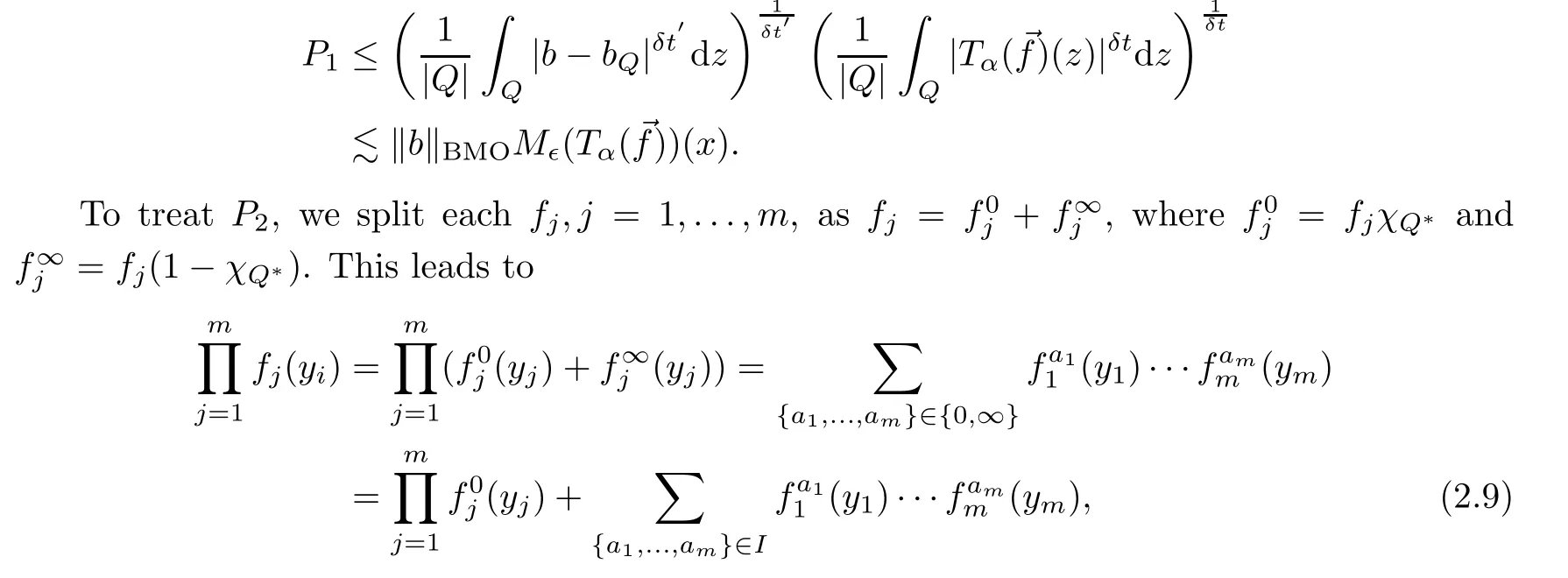
whereIis the collection of allm-tuplesa=(a1，...，am) with eachaj=0 or∞and at least oneaj=∞.Letting，we have that

To estimate，we first note that，for anys＞r，by the Hlder and John-Nirenberg inequalities，

It then follows from Lemma 2.3，the weak-type estimate onTα，and Hlder’s inequality，that

which implies that

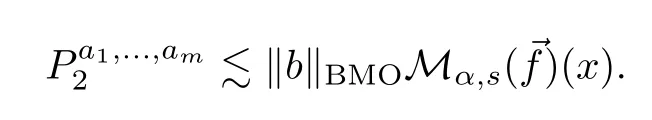
This concludes the proof of Lemma 2.9. □

3 Bounds for Multilinear Operators:Proofs of Theorems 1.1–1.10

Proof of Theorem 1.1Applying Lemma 2.8 withα2=0 and then Lemma 2.6，we obtain that

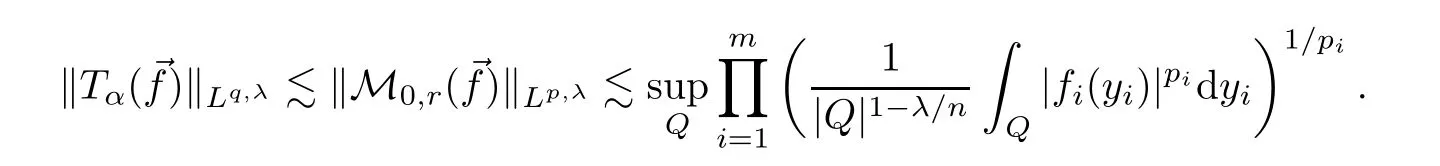
This proves Theorem 1.1. □

Proof of Theorem 1.3It follows by applying Lemma 2.8 that

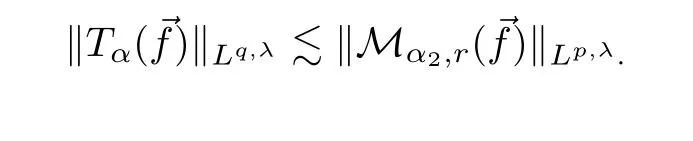
Using the definition of a multilinear fractional maximal operator，we see that，for anyx∈Rn，

This，together with Lemma 2.6，yields the desired inequality. □

Proof of Theorem 1.4Without loss of generality，we may assume thatf1，...，fmare nonnegative.

First，we will establish the following inequality:

Using inequality (2.2)，we only need to show that

Forj=2，...，m，we can deal with things using a similar method.Using the dual identity (2.3) and Lemma 2.4，

where the supremum is taken over nonnegative functionsg∈Hq′，λwith norm 1，and the last inequality follows from the estimate|x-y1|/m+|x-yi|≥|y1-yi|/m(i=2，...，m).

Using (3.3) and Theorem 1.1，we have that

which gives (3.2).

By the definition ofHq，λ，it is enough to show that

Sincew∈A1，by the property ofA1weight，we havew1-q∈Aq⊂A∞.Then，by Lemmas 2.2 and 2.7，we obtain that

Next，we look at

Now，we use Lemma 2.5 as follows:we write

since the mapw→wtis bijective onA1.Thus，we have

thanks to (3.1).Using Lemma 2.5 again，we deduce that

thereby reaching

This estimate，along with (3.5)，yields (3.4).Hence，the proof of Theorem 1.4 is finished. □

Proof of Theorem 1.5It suffices to show that，for any fixedQ⊂Rn，

wherecQdenotes some constant whose value will be determined later.Denote the left hand side asK.Using the same decomposition as in (2.9) and selectingwe have that

We first estimateK1.Since max (m/r，0)n＜α＜mn，there existsr*＞1 such that 1/r*=m/r-α.Then，using Lemma 2.3，Hlder inequality，and the fact thatp=λ/α，we have that

Next，we treatK2.By arguments similar to those in the proof of Lemma 2.9，we have that

This completes the proof of Theorem 1.5. □

4 Bounds for Commutators:Proofs of Theorems 1.8–1.11

Proofs of Theorems 1.8 and 1.9By Lemmas 2.2 and 2.9，it suffices to bound theLq，λ(quasi-norm offorr＜s＜min (p1，...，pm) and 0＜∈＜min (1，).Using Lemmas 2.2 and 2.7，we get that

The desired bound then follows from Lemma 2.6.This finishes the proof of Theorem 1.8.

Theorem 1.9 can be proven in the same manner，so we omit the details here. □

Proof of Theorem 1.10Choosesin Lemma 2.9 such thatr＜s＜q.Then，by using Lemmas 2.2 and 2.9，it suffices to prove the following inequality:

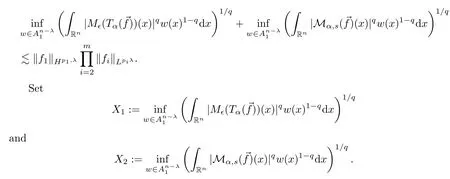
ForX1，using Lemmas 2.2 and 2.7，we have that

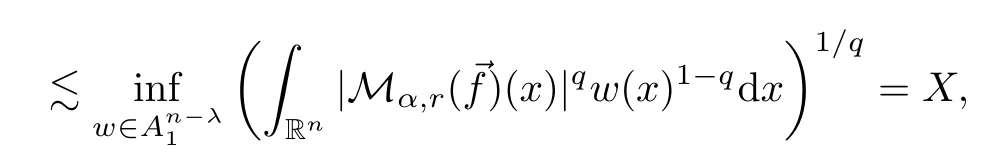
whereXis defined as in proof of Theorem 1.4.Then，we have that

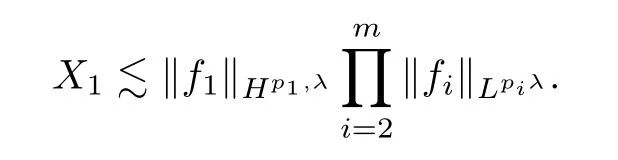
X2can be treated in the same way and the same bound can be obtained.This completes the proof of Theorem 1.10. □

Proof of Theorem 1.11By arguments similar to these in the proof of Lemma 2.9 and Theorem 1.5，we have that

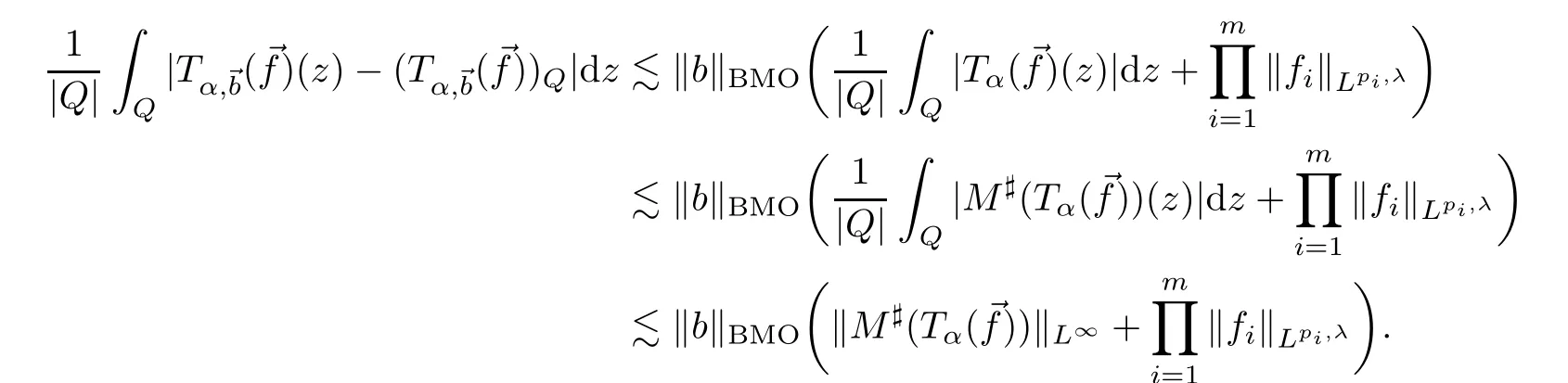
Using Theorem 1.5 and (2.1)，we get that

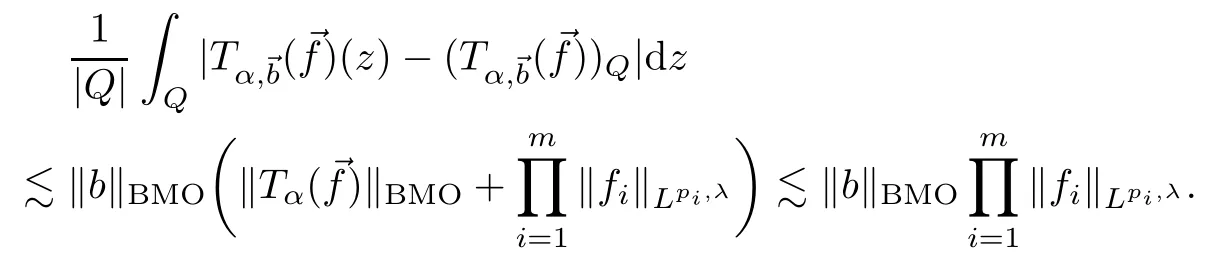
This concludes the proof of Theorem 1.11. □

Proof of Corollary 1.13Sinceb∈L∞⊂BMO，we have that

Using (4.1) and Theorem 1.12，we conclude that

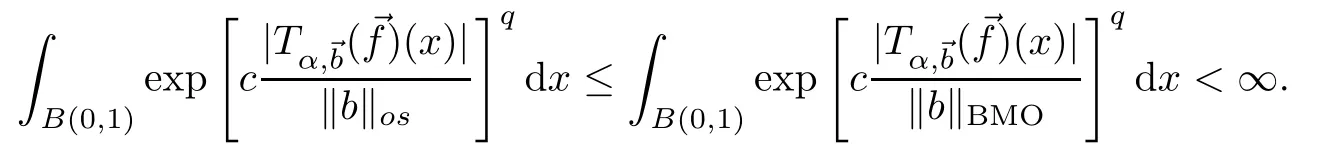
The proof of Corollary 1.13 is completed. □

5 Application to Multilinear Fourier Multipliers

Whenα=0，it is easy to see that the multilinearLr-Hrmander’s condition is weaker than that in[7].Moreover，our results also extend to the caseα＞0.In particular，we give some applications to multilinear Foureir multipliers in this last case，extending the results in[50].For more information about Fourier multipliers on Morrey spaces，we refer the reader to[19，27，32，36].

Fors∈R，the Sobolev spaceWs(Rnm) consists of allF∈S′(Rnm) such that

whereξ=(ξ1，...，ξm)∈Rn×···×Rn.

In this section，we consider the multilinear Fourier multiplierTmgiven by

forf1，...，fm∈S (Rn)，wheremsatisfies minimal Sobolev regularity.

Let Ψ∈S (Rnm) be such that supp Ψ⊂{ξ∈Rnm:1/2≤|ξ|≤2}andfor allξ∈Rnm{0}.For a functionm，α＞0 andk∈Z，we set

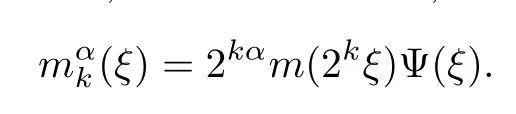
Then the limited Sobolev regularity condition reads as follows:

The caseα=0 corresponds to the multilinear singular integral case studied in[22，24，25，50]，where theLp1×···×Lpn→Lpbounds were established for appropriate 1/2＜p＜∞，1＜p1，...，pm＜∞，under (5.1).The regularity conditions＞nm/2 in (5.1) is minimal in the sense thatnm/2 cannot be replaced by any smaller constant.TheLp1，λ×Lp2，λ×···×Lpm，λ→Lp，λboundedness was obtained in[51]forp＞1，and was left open for 1/2＜p≤1.

The caseα＞0 corresponds to the fractional integrals case considered in[11，25]，where the mapping properties in Lebesgue space were studied.The Morrey space bounds for smooth multilinear fractional integrals were obtained by[51]，but the case of multilinear fractional Fourier multipliers with minimal Sobolev regularity was left open.

Applying Theorem 1.1，we are able to treat both cases in a unified manner，and obtain Morrey space boundedness for a full range of indices，which answers the above mentioned questions.

Theorem 5.1Let 1＜p1，...，pm＜∞，1/p=1/p1+···+1/pm，0＜α＜n/p，1/q=1/p-α/n，s＞nm/2 andr=max (1，nm/(s+α))＜p1，...，pm，mp.Suppose thatmsatisfies (5.1).Then，

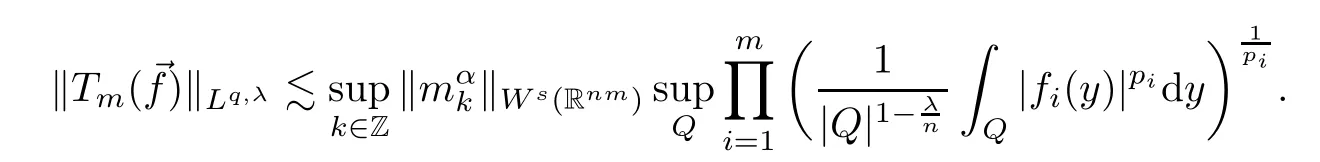
ProofLetsatisfyr＜＜p1，...，pm，mp.In order to prove Theorem 5.1，it suffices to verify the hypothesis of Theorem 1.1 withrreplaced.Thus，however，was done in the proof of Theorem 5.1 in[11]. □

Remark 5.2In a manner similar to Theorem 5.1，Theorems 1.3，1.4，1.8，1.9 and 1.10 can be applied to multilinear Fourier multipliersTmwith minimal Sobolev regularity，and similar results can be derived.We leave the details to the interested reader.