A ROBUST COLOR EDGE DETECTION ALGORITHM BASED ON THE QUATERNION HARDY FILTER*
Wenshan BI (毕文姍)
Department of Mathematics,Faculty of Science and Technology,University of Macau,Macau,China
E-mail:wenshan0608@163.com
Dong CHENG (程冬)
Research Center for Mathematics and Mathematics Education, Beijing Normal University at Zhuhai,Zhuhai 519087, China
E-mail : chengdong720@163.com
Wankai LIU (刘万凯)
School of Mathematics and Quantitative Economics,Shandong University of Finance and Economics,Jinan 250014,China
E-mail:zjnulwk@163.com
Kit Ian KOU (高洁欣)†
Department of Mathematics,Faculty of Science and Technology,University of Macau,Macau,China
E-mail:kikou@um.edu.mo
Abstract This paper presents a robust filter called the quaternion Hardy filter (QHF) for color image edge detection.The QHF can be capable of color edge feature enhancement and noise resistance.QHF can be used flexibly by selecting suitable parameters to handle different levels of noise.In particular,the quaternion analytic signal,which is an effective tool in color image processing,can also be produced by quaternion Hardy filtering with specific parameters.Based on the QHF and the improved Di Zenzo gradient operator,a novel color edge detection algorithm is proposed;importantly,it can be efficiently implemented by using the fast discrete quaternion Fourier transform technique.From the experimental results,we conclude that the minimum PSNR improvement rate is 2.3%and the minimum SSIM improvement rate is 30.2%on the CSEE database.The experiments demonstrate that the proposed algorithm outperforms several widely used algorithms.
Key words Boundary values;color image edge detection;quaternion analytic signal;discrete quaternion Fourier transform
1 Introduction
Edge detection is a fundamental problem in computer vision[1–3].It has a wide range of applications,including medical imaging[4],lane detection[5],face recognition[6],weed detection[7]and deep learning[8].The well-known method also plays an essential role in image processing and data analysis[9–11].
1.1 Related works
Sobel,differential phase congruence (DPC) and modified differential phase congruence (MDPC) detectors have drawn wide attention and achieved great success in gray-scale edge detection[12–14].Another approach of edge detection is detecting edges independently in each of the three color channels,and then obtaining the final edge map by combining three single channel edge results according to some proposed rules[15].However,these methods ignore the relationship between different color channels of the image.Instead of separately computing the scaled gradient for each color component,a multi-channel gradient edge detector has been widely used since it was first proposed by Di Zenzo[16].Later,Jin[17]solved the uncertainty of the Di Zenzo gradient direction and presented an improved Di Zenzo (IDZ) gradient operator which achieves a significant improvement over DZ.However,the IDZ gradient operator is not stable against noise[17].
A growing amount of research[18–20]indicates that quaternions are well adapted to color image processing by encoding color channels into three imaginary parts.It is worth noting that Ell et al.proposed an important color image edge detection method in[21].This uses genuine quaternionic Prewitt inspired techniques for edge detection.The quaternion analytic signals are the boundary values of the functions in quaternion Hardy space[22].Based on the quaternion analytic signal,researchers in[23]proposed some phase-based algorithms to detect the edge map of gray-scale images.It was shown that the introduction of a quaternion analytic signal can reduce the influence of noise on edge detection results.It should be noted that although the tool of the quaternion was applied,the algorithms (QDPC and QDPA) in[23]only considered gray-scale images.Based on the quaternion Hardy filter and the IDZ gradient operator,we propose a novel edge detection algorithm which can be applied to color images.
1.2 Paper contributions
The contributions of this paper are summarized as follows:
1.We propose a novel filter,named the quaternion Hardy filter (QHF),for color image processing.Compared with the quaternion analytic signal,our method has better performance due to the flexible parameter selection of QHF.
2.Based on the QHF and the improved Di Zenzo gradient operator,we propose a robust color edge detection algorithm.This can enhance the color edge in a holistic manner by extracting the main features of the color image.
3.We set up a series of experiments to verify the denoising performance of the proposed algorithm in various environments.Visual and quantitative analysis are both conducted.Three widely used edge detection algorithms,Canny,Sobel,and Prewitt,and recent edge detection algorithms,QDPC,QDPA,DPC,and MDPC,are compared with the proposed algorithm.In terms of peak SNR (PSNR) and similarity index measure (SSIM),the proposed algorithm presents a superiority in terms of edge detection.
1.3 Paper outline
The rest of the paper is organized as follows:Section 2 recalls some preliminaries of the improved Di Zenzo gradient operator,quaternions,the quaternion Fourier transform,quaternion Hardy space,and the quaternion analytic signal.Section 3 presents the main result of the paper and defines the novel algorithm for color-based edge detection of real-world images.Experimental results of the proposed algorithm are shown in Section 4.Conclusions and discussions of future work are discussed in Section 5.It is worth noting that all the figures are better viewed in a zoomed PDF.
2 Preliminaries
This part recalls some preparatory knowledge regarding the improved Di Zenzo gradient operator[17],quaternions,the quaternion Fourier transform[24],quaternion Hardy space[23],and the quaternion analytic signal[25]which will be used throughout the paper.
2.1 The improved Di Zenzo gradient operator
In this section,we recall the improved Di Zenzo gradient operator,namely the IDZ gradient operator.It will be combined with the quaternion Hardy filter to establish the novel edge detection algorithm in the next section.
Letfbe anM×Ncolor image that maps a point (x1,x2) to a vector (f1(x1,x2),f2(x1,x2),f3(x1,x2)).Then the square of the variation offat the position (x1,x2) with the distanceγin the directionθis given by
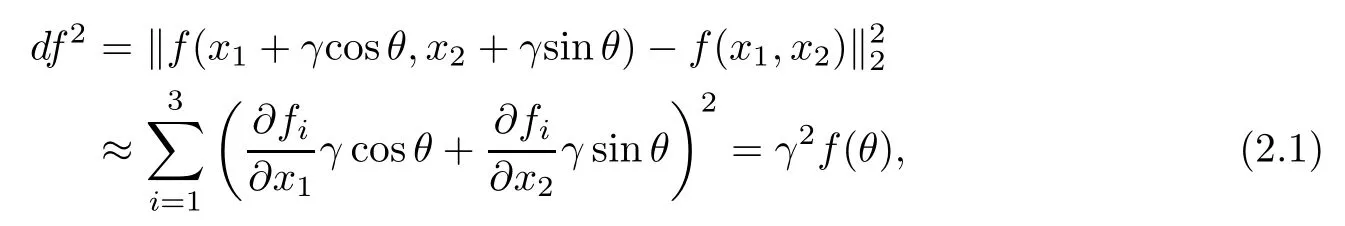
where ‖·‖ represents 2-norm,and the rate of change of the imagefat position (x,y) in any directionθis given by

Then the gradient magnitudegmaxof the improved Di Zenzo’s gradient operator is given by
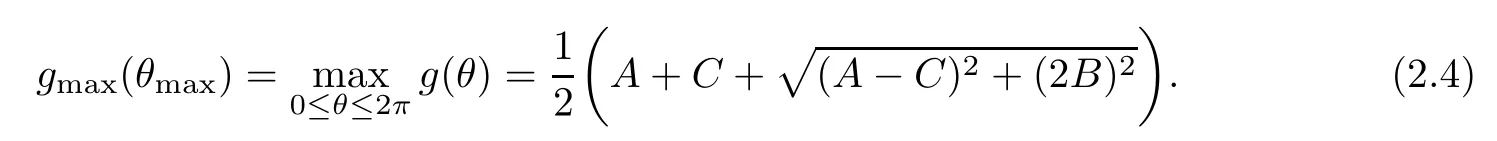
The gradient direction is defined as the valueθmaxthat maximizesg(θ) over 0≤θ≤2π,
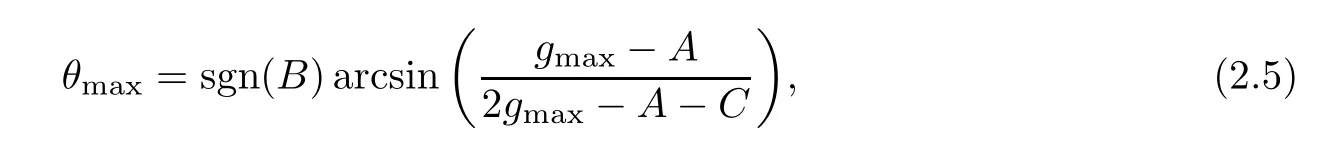
where (A-C)2+B20,,θmaxis undefined.
It is important to note that the IDZ gradient operator is designed to process real domain signals and does not possess the capability of de-noising.
2.2 Quaternions
As a natural extension of the complex space C,the quaternion space H was first proposed by Hamilton[26].A complex number consists of two components:one real part and one imaginary part.A quaternionq∈H has four components,i.e.,one real part and three imaginary parts

whereqn∈R,n=0,1,2,3,and the basis elements{i,j,k}obey the Hamilton multiplication rules
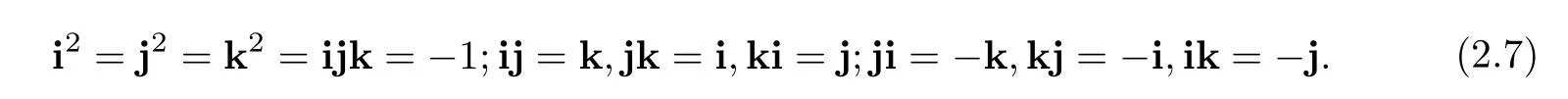
Given a quaternionq=q0+q1i+q2j+q3k,its quaternion conjugate is:=q0-q1i-q2j-q3k.We writewhich are the scalar and vector parts ofq,respectively.This leads to a modulus ofq∈H defined by
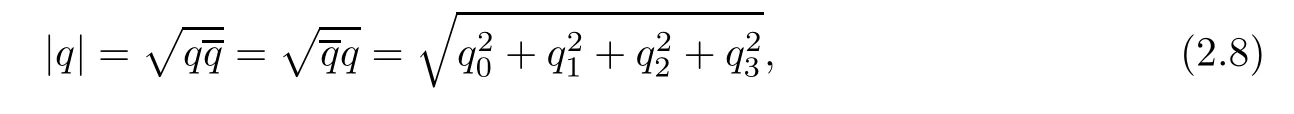
whereqn∈R,n=0,1,2,3.
By (2.6),an H-valued functionf:R2→H can be expressed as
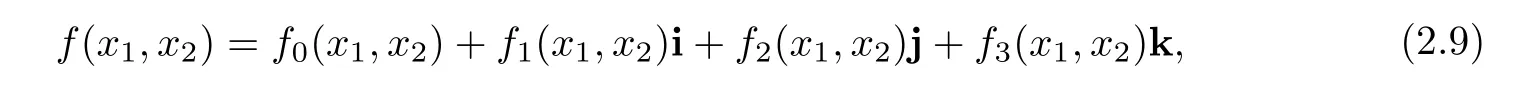
wherefn:R2→R (n=0,1,2,3).In this paper,we consider usingf(x1,x2) to represent a color image,i.e.,f(x1,x2)=f1(x1,x2)i+f2(x1,x2)j+f3(x1,x2)k.Meanwhile,f1,f2andf3represent,respectively,the red,green and blue components of the color image.
2.3 Quaternion Fourier transform
Suppose thatfis an absolutely integrable complex function defined on R.Then the Fourier transform[27]offis given by
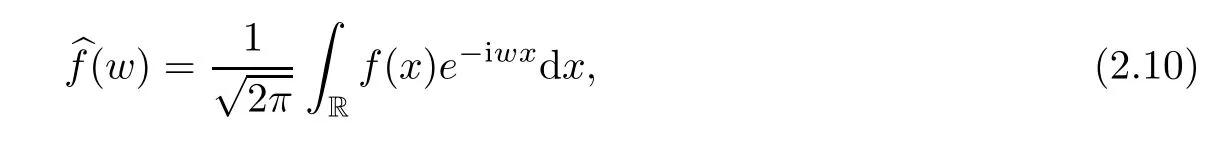
wherewdenotes the angular frequency.Moreover,ifbfis an absolutely integrable complex function defined on R,thenfcan be reconstructed by the Fourier transform offand is expressed by
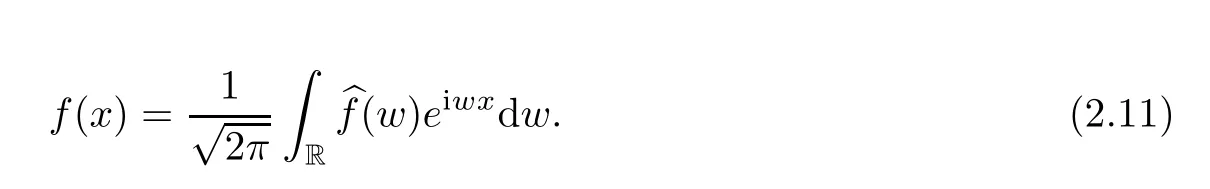
The quaternion Fourier transform,regarded as an extension of the Fourier transform in the quaternion domain,plays a vital role in grayscale image processing.The first definition of the quaternion Fourier transform was given in[28]and the first application to color images was discussed in[29].Wide-ranging non-commutative multivector Fourier transform generalizations of the quaternion Fourier transform were discussed in[24],and it was recently applied to find the envelope of the image[30].The application of the quaternion Fourier transform on color images was discussed in[20,31].The Plancherel and inversion theorems of the quaternion Fourier transform in the square integrable signals class were established in[32].Due to the non-commutativity of the quaternions,there are various types of quaternion Fourier transforms.In what follows,we focus our attention on the two-sided quaternion Fourier transform (QFT).
Suppose thatfis an absolutely integrable H-valued function defined on R2.Then the continuous quaternion Fourier transform offis defined by
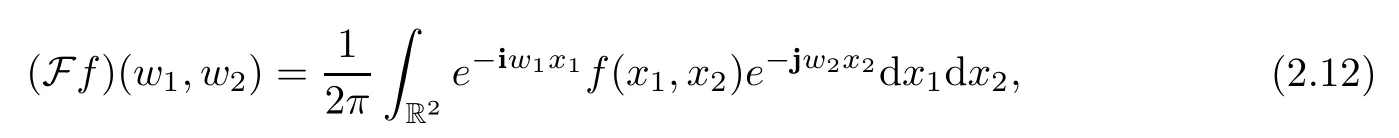
wherewlandxldenote the 2D angular frequency and 2D space (l=1,2),respectively.Equation (2.12) is only a special case of a much more general definition of QFT (see[24]for more details).For the general definition of QFT,however,the choice of the units in the kernel factors can be very flexible.The choice of two orthogonal units i and j,in the kernel factors,can be selected by any two pure quaternions,not necessarily orthogonal units,and will produce similar properties (see[33]for more details).
Furthermore,iffis an absolutely integrable H-valued function defined on R2.Then the continuous inverse quaternion Fourier transform (IQFT) offis defined by
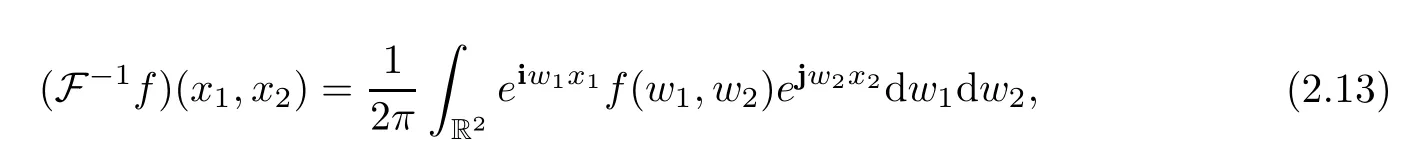
wherewlandxldenote the 2D angular frequency and 2D space (l=1,2),respectively.
The discrete quaternion Fourier transform (DQFT) and its inverse was introduced by Sangwine[29].Suppose that the discrete arrayf(m,n) is of dimensionM×N.The DQFT has the form
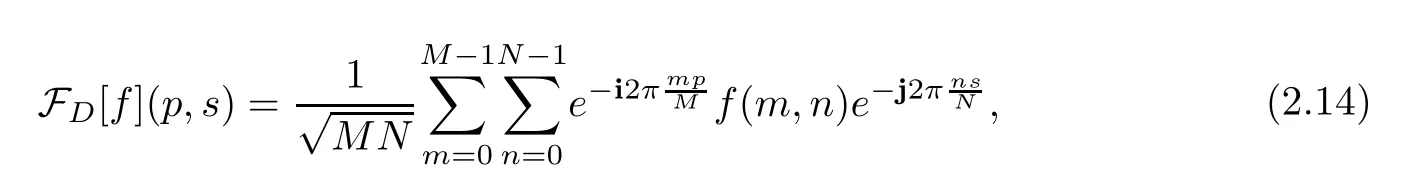
wherepandsare the variables in the frequency domain.The inverse discrete quaternion Fourier transform (IDQFT) is
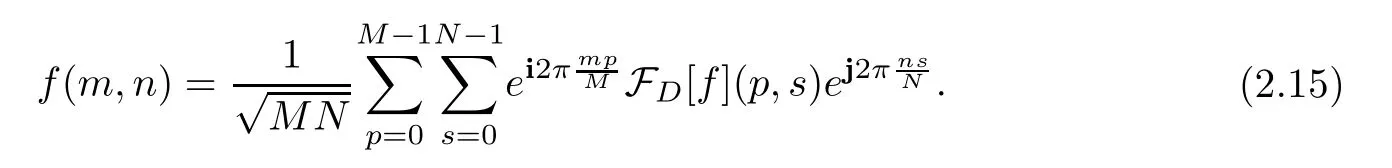
2.4 Quaternion Hardy space
Let C={z|z=x+si,x,s∈R}be the complex plane,and let a subset of C be defined by C+={z|z=x+si,x,s∈R,s>0},namely the upper half complex plane.The Hardy spaceH2(C+) on the upper half complex plane consists of functionscsatisfying the following conditions:
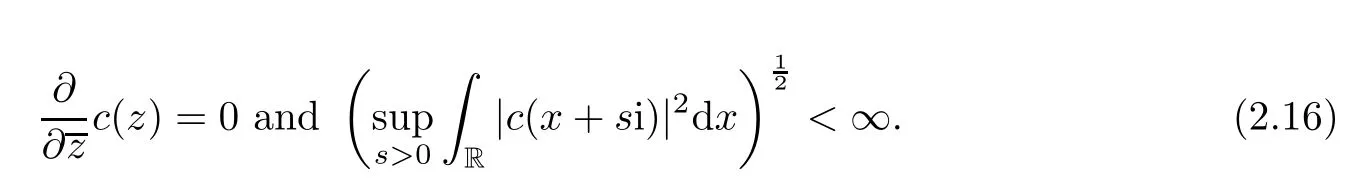
The generalization[20]to higher dimension is given as follows:let Cij={(z1,z2)|z1=x1+s1i,z2=x2+s2j,xl,sl∈R,l=1,2}and let a subset of Cijbe defined by={(z1,z2)|z1=x1+s1i,z2=x2+s2j,xl,sl∈R,sl>0,l=1,2}.The quaternion Hardy spaceconsists of all functions satisfying

2.5 Quaternion analytic signal
In what follows,we review the concept of the analytic signal.Given a real signalf,combined with its own Hilbert transform,the analytic signal offis given by
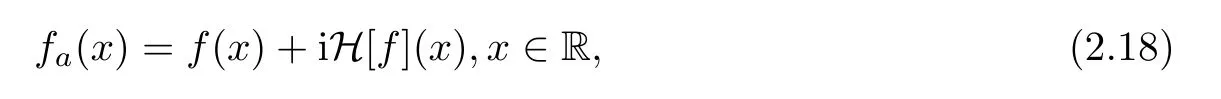
where H[f]denotes the Hilbert transform offand is defined by

The Fourier transform of an analyticfadefined in (2.18) is given by

wherew∈R.
A natural extension of the analytic signal from 1D to 4D space in the quaternion setting is called the quaternion analytic signal;it was proposed by Bülow and Sommer[25]using partial and total Hilbert transforms associated with QFT.Given a 2D quaternion-valued signalf,combined with its own quaternion partial and total Hilbert transforms,we get a quaternion analytic signalfq[25]as

are the quaternion partial Hilbert transforms offalong thex1-axis andx2-axis,respectively.Meanwhile,
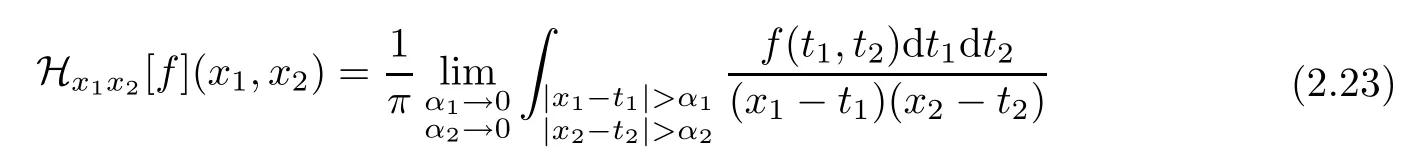
is the quaternion total Hilbert transform along thex1andx2axes.By direct computation,the quaternion Fourier transform of quaternion analytic signal is given by
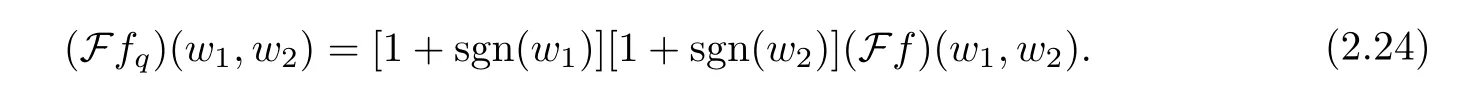
3 Proposed Algorithm
In this section,we introduce our new color edge detection algorithm.To begin with,the definition of the quaternion Hardy filter is presented.
3.1 Quaternion Hardy filter
The quaternion analytic signalfqcan be regarded as the output signal of a filter with inputf.The system function of this filter is
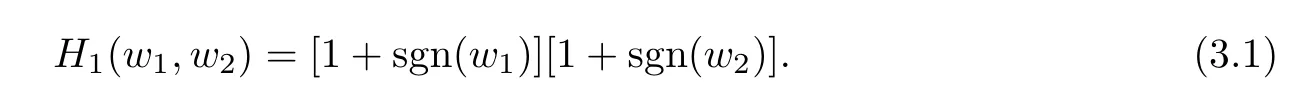
In this paper,we use a novel filter,named the quaternion Hardy filter (QHF),to construct a high-dimensional analytic signal.The system function of QHF is defined by
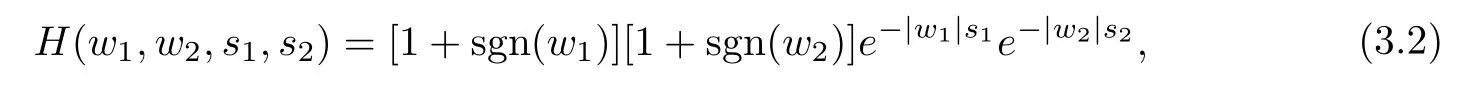
wheres1≥0,s2≥0 are parameters of the system function.The factors (1+sgn (w1))(1+sgn (w2)) ande-|w1|s1e-|w2|s2play different roles in the quaternion Hardy filter.The former performs a Hilbert transform on the input signal,while the later plays the role of suppressing the high-frequency.First,the Hilbert transform operation can selectively emphasize the edge feature of an input object.Second,the low pass filtering can improve the ability of noise immunity for the QHF.It can be seen that with increasings1,s2,the effect of inhibiting for the high frequency becomes more obvious.In particular,ifs1=s2=0,thene-|w1|s1e-|w2|s2=1,and it follows that
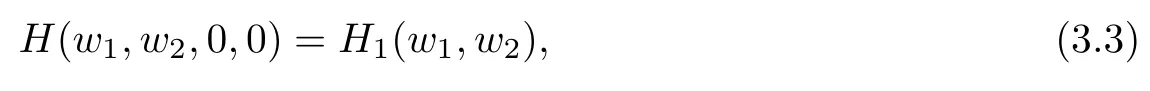
which means that there is no effect of high frequency inhibiting.All of this is to say that if the interference of noise for the input signal is negligible,we can set the parameterss1,s2to be 0.
The parameterss1ands2control the low pass filtering in vertical and horizontal directions,respectively.When the signal frequencies in the two directions are similar,thens1ands2can be set to the same value.If the signal frequencies in these two directions are different,thens1ands2should be different.For example,if the horizontal noise in the image is large,the value ofs2should be set larger to enhance the anti-noise ability in that direction.This means that the QHF is more general and flexible,and it can solve a wide range of problems that cannot be solved well only by the quaternion analytic signal.

For any fixeds1,s2≥0,denote byfH(x1,x2,s1,s2) the output signal of the QHF with inputf(x1,x2).By the definition,we have
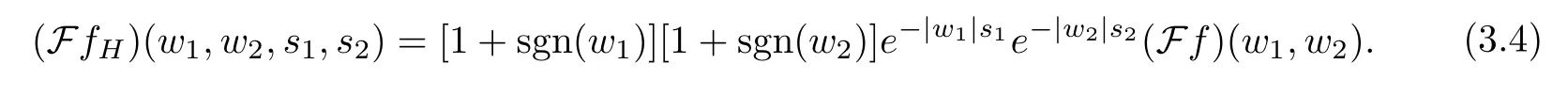
Here,the QFT acts on the variablex1,x2.We will show that as a function ofz1=x1+is1andz2=x2+js2,fHbelongs to the quaternion Hardy space.
Theorem 3.1Letf∈L2(R2,H) andfHbe given as above.ThenfH∈.
ProofUsing inverse quaternion Fourier transform defined by Equation (2.13),we have that
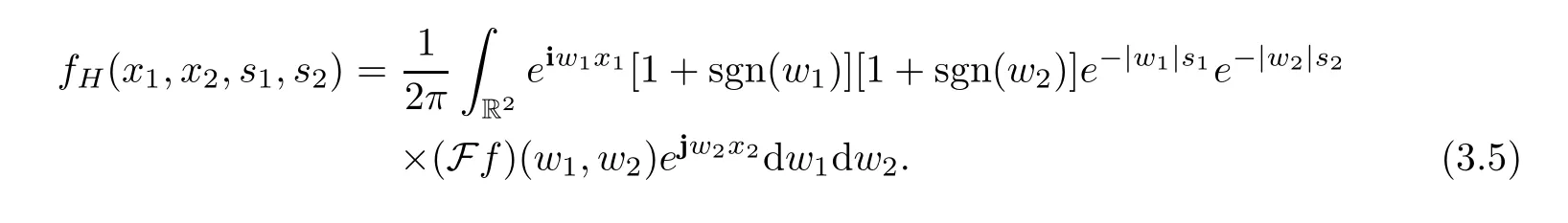
Taking the derivative offHwith respect towe get
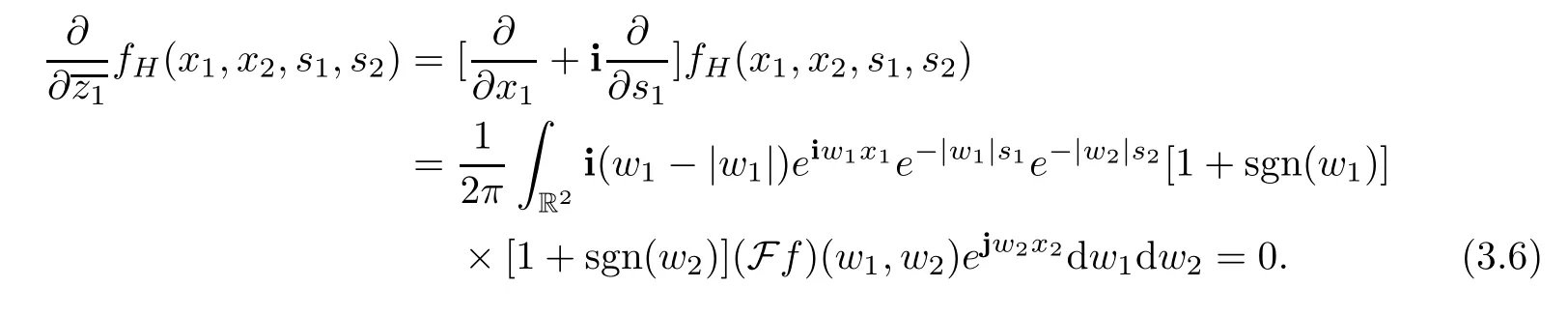
The last equality holds,since the integrand vanishes identically.Similarly,
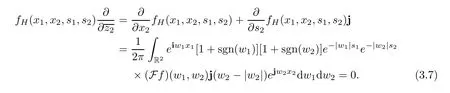
For any fixeds1>0,s2>0,from (3.4) we can obtain that

According to the QFT Parseval’s identity[32],we obtain that
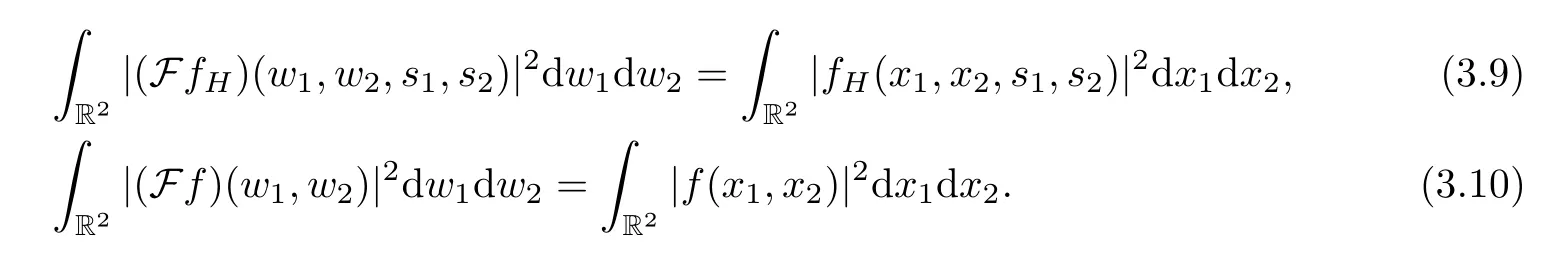
Using (3.8),(3.9) and (3.10),a direct computation shows that
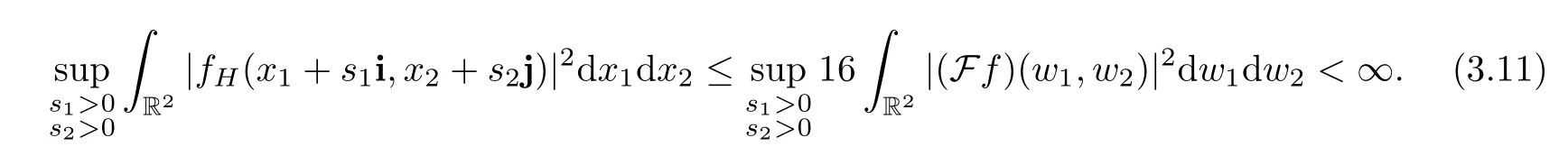
The proof is complete. □
3.2 Color edge detection algorithm
In this section,the edge detector based on the QHF is described.First,we obtain the high-dimensional analytic signal of the original image through QHF.Second,the obtained high-dimensional analytic signal is used as the input of the IDZ gradient operator.Finally,we get the result of the edge detection.Figure 1 shows the block diagram of the proposed algorithm.Let us now give the details of the quaternion Hardy filter based algorithm.These are divided into the following steps:

Figure 1 Block diagram of the proposed algorithm
Step 1Take an input digital color imagefof sizeM×N.Associate it with a H-valued signal

wheref1,f2andf3represent,respectively,the red,green and blue components of the given color image.
Step 2Compute the DQFT of thefusing equation (2.14).The result will be FD[f].
Step 3For fixeds1>0,s2>0,the values of parameterss1ands2of the original image ranged from 1.0 to 2.0,and those of the noisy image ranged from 1.0 to 8.0,multiplying FD[f]by the system function (3.2) of the QHF.Then we obtain the DQFT offHwhich has the following form:
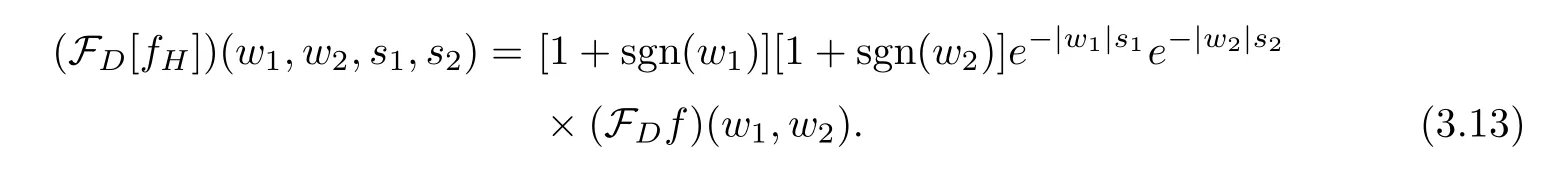
This is the most significant step in our algorithm,because it allows for the advantages of QHF as we described.
Step 4Computing the inverse DQFT of FD[fH]by applying equation (2.15),we obtainfH.
Step 5Extracting the vector part offH,we obtain

wherehk,k=1,2,3 are real-valued functions.In what follows,we will apply the IDZ gradient operator based onVec(fH) instead off.
Step 6Perform the IDZ gradient operator forVec(fH).Applying equation (2.3),we obtain
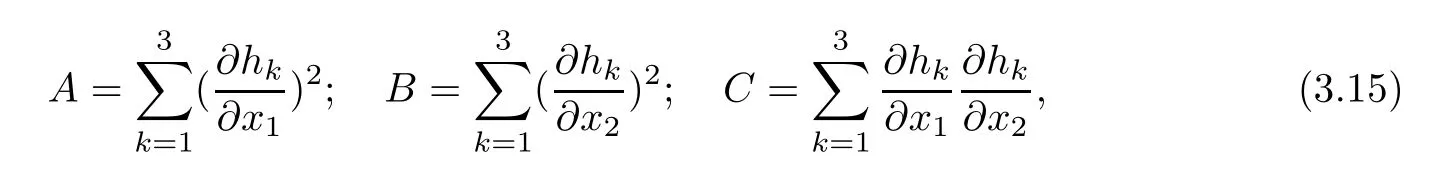
then we substitute this into equation (2.4),obtaining
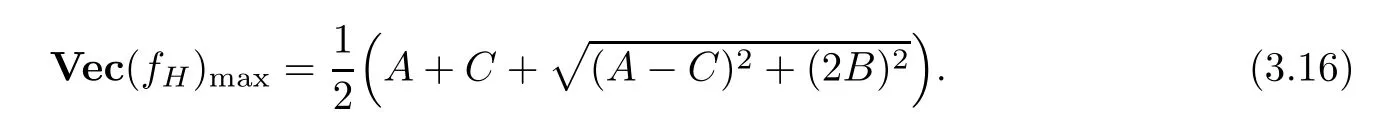
Step 7Finally,we obtain the processed result,an edge map,by applying the nonmaximum suppression.
We assume,for simplicity,thatM=N.It is easy to see that the main computation complexity lies in the QFT.According to[29],the computational complexity of QFT for anM×Mimage is about O (M2log2M).The computational complexity of the remaining steps is approximately O (M3).Therefore,the whole computational complexity of the proposed algorithm is about O (M2log2M)+O (M3).The computational cost of MDPC algorithm is about O (M2log2M).The computational complexity of both QDPC and QDPA algorithm is O (M2log2M).
4 Experimental Results
In this section,we shall demonstrate the effectiveness of the proposed algorithm for color image edge detection.
Here both visual and quantitative analysis for edge detection are considered in our experiments.All experiments were programmed in Matlab R2016b.To validate the effectiveness of the proposed method,we carried out verification on four databases (sample images are shown in Figures 2–5).
Figure 2 is a database made up of eight images,which we have named the“classic database”in this paper.Except for T2,all the images in Figure 2 are partial images from[34]and the Corel database.Image T2 is taken by Wenshan Bi on Father’s Day.The reason we chose these images is that most of the images in Figure 2 are commonly used in image processing.

Figure 2 Sample images from the classic database.From left to right and top to bottom:Lena,House,Men,T1,T2,T3,Cara and Frog
The images in Figure 3 are randomly selected from the synthetic database[35].This database was provided by Université de Lille in France.

Figure 3 Sample images from the synthetic database[35]
The test images in Figure 4 are randomly selected from the CSEE database[36].This database can be found in[1,2].

Figure 4 Sample images from the CSEE database[36]
The images in Figure 5 are randomly selected from the scene database[37].This database was provided by Universidad de Granada and the Computer Vision Group,and it consists of 805 test images with 3 different size scales.

Figure 5 Sample images from the scene database[37]
Here,the Gaussian filter[38,39]is applied to these algorithms (Canny[40],Sobel,Prewitt[41],DPC,and MDPC),since they did not consider the noise image edge detection problem.Digital images have been distorted with different types of noise such as I-Gaussian noise[42],II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise.The ideal noiseless and noisy images are both taken into account.
4.1 Visual comparisons
In terms of visual analysis,the IDZ gradient operator and seven widely used and noteworthy methods,QDPC,QDPA,Canny,Sobel,Prewitt,Differential Phase Congruence (DPC) and Modified Differential Phase Congruence (MDPC),will be compared with our algorithm.
4.1.1 Color-based algorithm
In this part,we compare the proposed algorithm with the IDZ gradient operator.In order to make the experiment more convincing,we used the Gaussian filter before the IDZ gradient operator to achieve the effect of denoising.Figure 6 presents the edge maps of the noiseless House image,while Figure 7 presents the edge maps of the House image corrupted with four different types of noise.It can be seen from the second row of Figure 7 that the IDZ gradient operator performs well in the first two images of the first row,while it performs poorly in the last two images.This illustrates the IDZ gradient operator’s limitations as an edge detector.The third row of Figure 7 shows the detection results of the proposed algorithm;it preserves details more clearly than the second row.It demonstrates that the proposed algorithm gives robust performance compared to that of the IDZ gradient operator.

Figure 6 The noiseless House image (left).The edge maps obtained by the IDZ gradient operator (middle) and the proposed algorithm (right)

Figure 7 The first row is the noisy House image with additive Gaussian noise,Poisson noise,Salt&Pepper noise and Speckle noise,from left to right.The second and third rows are the edge maps which are captured by the IDZ gradient operator and the proposed algorithm,respectively
4.1.2 Grayscale-based algorithms
We compare the performance of the proposed algorithm with seven widely used and noteworthy algorithms.The noiseless (Figures 2–5) and noisy images are both taken into consideration.Here,the commonly used color-to-gray conversion formula[43,44]is applied in the experiments;it is defined as follows:
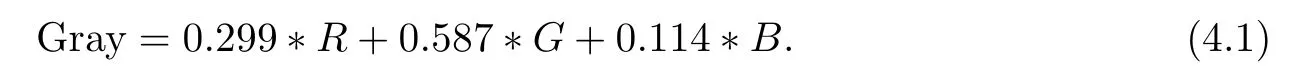
·Noiseless case:In total,we selected two images from four data sets as test images to show the edge detection effect under noiseless conditions.In other words,an image in the first row and the second column is selected from Figure 3,and then an image in the first column of the third row is selected from Figure 4.The edge detection results of these two images are shown in Figure 8 and Figure 9,respectively.Different rows and columns correspond to the results of different methods.From left to right and top to bottom they are QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithms,respectively.The results show that these eight methods are ideal for noiseless images.

Figure 8 Edge maps of a randomly selected noiseless image (the first row and second column of Figure 3,namely GREEN).From left to right and top to bottom:QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithm

Figure 9 Edge maps of a randomly selected noiseless image (from the CSEE database,namely Stapler) given by different algorithms.From left to right and top to bottom:QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithm
·Noisy case:Here,we add four different noises (I-IV) to each image selected above.The edge maps obtained by applying the QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed method to noisy images are shown in Figures 10–13 and Figures 14–17,respectively.Figure 10 and Figure 11 show that the Canny algorithm performs quite well.Furthermore,in Figure 15,for example,a number of other filters show the fuzzy edges of the white paper under the stapler (in the lower left corner of the stapler picture).On close observation,however,we found that some of the images have erroneous detected edges.The main reason is that the noise interference to the white paper is so strong that the edge and noise cannot be distinguished.The result of edge detection presented by the proposed algorithm is very clear,but a small proportion of edges fail to be detected.In order to overcome this limitation,we will work on a theory of boundary enhancement to optimize our algorithm in future work.In general,the proposed algorithm is able to extract edge maps from the noisy images.This means that the proposed algorithm is resistant to the noise.In particular,the algorithm is superior to the other detectors on images with noise III and IV.
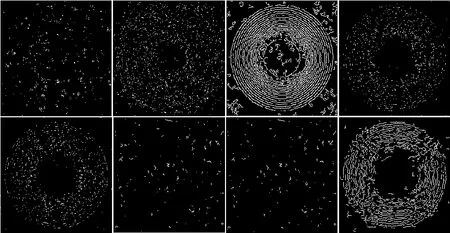
Figure 10 The edge maps of the noisy Green image (with additive Gaussian noise) given by different algorithms.From left to right and top to bottom:QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithm

Figure 12 The edge maps of the noisy Green image (with additive Salt&Pepper noise) given by different algorithms.From left to right and top to bottom:QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithm

Figure 13 The edge maps of the noisy Green image (with additive Speckle noise) given by different algorithms.From left to right and top to bottom:QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithm

Figure 14 The edge maps of the noisy Stapler image (with additive Gaussian noise) given by different algorithms.From left to right and top to bottom:QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithm

Figure 15 The edge maps of the noisy Stapler image (with additive Poisson noise) given by different algorithms.From top to bottom:QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithm

Figure 16 The edge maps of the noisy Stapler image (with additive Salt&Pepper noise) given by different algorithms.From top to bottom:QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithm

Figure 17 The edge maps of the noisy Stapler image (with additive Speckle noise) given by different algorithms.From top to bottom:QDPC,QDPA,Canny,Sobel,Prewitt,DPC,MDPC and the proposed algorithm
4.2 Quantitative analysis
The PSNR[45]is a widely used method of objective evaluation of two images.It is based on the error-sensitiveimage quality evaluation.In addition,the SSIM[46]is a method of comparing two images under the three aspects of brightness,contrast,and structure.To show the accuracy of the proposed edge detector,the average PSNR and SSIM of various edge detectors on noisy images (I-Gaussian noise,II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise) are calculated (Tables 1–8).Each value in the table represents the similarity between the edge map of the noisy image and the edge map of the noiseless image;that is,the larger the value,the stronger the denoising ability.
Table 1 shows the average PSNR value of the experimental results of Figure 2.In the case of the noise I,Sobel and QDPC have the highest PSNR values,and the method proposed in this paper ranks third.In the case of the noise II,Sobel and Prewitt had the highest PSNR,and the method proposed in this paper still ranked third.In the case of noises III and IV,QDPC had the highest PSNR value,and the method proposed in this paper was followed by QDPC in second place.
In general,the method proposed in this paper ranks in the top three among the eight methods compared.This shows that these three algorithms can achieve high similarity between the edge maps of a noisy image and a noiseless image.Therefore,from the point of view of PSNR value,these three algorithms have better robustness than the others.
Table 2 shows the average SSIM value of the experimental results of Figure 2.From the table,it is clear that the method presented in this article has the highest SSIM value.In addition to the proposed method,the SSIM values of QDPC and Prewitt are very high as well.
Compared with QDPC,the improvement rates of SSIM for our algorithm under the four noise conditions were 17.2%,26.6%,17.4%,and 15.6%,respectively.Compared with Prewitt,the SSIM improvement rates of the four noise conditions were 7.5%,4.8%,26.8%,and 4.9%,respectively.On the whole,the proposed method significantly outperforms the others in terms of color edge detection on this type of images.
Table 3 shows the average PSNR values of the experimental results of Figure 3.There is no doubt that the proposed method has the highest value under all noise conditions,though it is worth noting that the differences are small.After calculation,we found that the improvement rate was less than 1%compared to the second best method (Canny).This indicates that,from the perspective of PSNR,the proposed edge detection method has only a slight improvement on Figure 3.
Tables 4 shows the SSIM values between the ground truth and the edge maps of the noisy images of Figure 3.We know that the closer the SSIM value is to 1,the better the performance of the algorithm is.From the average SSIM values in the table,the proposed method was optimal and improved by 9.9%,8.4%,12.3%,and 12.6%,respectively,compared with the second-place method (MDPC) under the four noise conditions.

Table 1 The PSNR comparison values for Figure 2.Types of noise:I-Gaussian noise,II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise

Table 2 The SSIM comparison values for Figure 2.Types of noise:I-Gaussian noise,II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise

Table 3 The PSNR comparison values for Figure 3.Types of noise:I-Gaussian noise,II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise

Table 4 The SSIM comparison values for Figure 3.Types of noise:I-Gaussian noise,II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise
Table 5 shows the average PSNR values of experimental results of Figure 4.The PSNR value of the proposed method is the highest,and is 3.1%,6.3%,3.3%,and 2.3%higher than that of the second-place method (Prewitt) under the four noise conditions.
Table 6 shows the average SSIM values of experimental results of Figure 4.The SSIM value of the proposed method is the highest,and is 40.8%and 41.7%higher than that of the second method (Prewitt) under the noise conditions I and IV.For the noise conditions II and III,the proposed method improved by 30.2%and 81.3%,respectively,compared with the second-place method (QDPA).
The average PSNR values of the experimental results in Figure 5 are shown in Table 7.The optimal and second-place methods are the proposed method and Prewitt,respectively.Compared with Prewitt,the improvement rates of the proposed method under the four noise conditions are 1.1%,3.8%,1.4%,and 2.3%,respectively.
The average SSIM values of the experimental results in Figure 5 are shown in Table 8.The top two methods are the proposed method and Prewitt.Compared with Prewitt,the improvement rates of the proposed method under the four noise conditions are 19.5%,23.3%,69.4%,and 28.2%,respectively.As apposed to the PSNR,the advantage of our method in SSIM over the others is more significant.Compared with the improvement rate of PSNR in Table 7,it is obvious that SSIM has a higher improvement rate.This indicates that the proposed method maintains the structure of Figure 5 well in the case of the four different types of noises.

Table 5 The PSNR comparison values for Figure 4.Types of noise:I-Gaussian noise,II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise

Table 6 The SSIM comparison values for Figure 4.Types of noise:I-Gaussian noise,II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise

Table 7 The PSNR comparison values for Figure 5.Types of noise:I-Gaussian noise,II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise

Table 8 The SSIM comparison values for Figure 5.Types of noise:I-Gaussian noise,II-Poisson noise,III-Salt&Pepper noise,and IV-Speckle noise
5 Conclusion
In this paper,we introduced a novel quaternion Hardy filter technique for color image processing.With the help of this technique,a color edge detection method was developed.QHF was not only adapted to feature enhancement but also used to handle different types of noises.Specifically,the IDZ gradient operator was considered,and it was improved significantly by introducing the QHF.The experimental results of edge detection on four databases were presented to illustrate the feasibility and effectiveness of the proposed method.
It is noted that the proposed algorithm still has limitations.The proposed method contains both the advantages of QHF and IDZ,as well as their disadvantages.Compared with other methods,the computational complexity cost of the proposed method is relatively high.Using low-rank quaternion tensor techniques[47]might make our approach better in terms of reducing computing costs.Furthermore,we need to enhance the denoising capability of QHF further by introducing some other novel effective techniques (see e.g.[48]).As for future work,we will study the fast numerical implementation for the proposed method,and apply the fast edge detection algorithm to the application of the visual synchronous localization and mapping.
Appendix
Tables 9–16 give the parameter settings for the comparison experiments of the classic database.
Table 9 Parameter settings for image of Lena in Table 1 and Table 2
Table 10 Parameter settings for image of Men in Table 1 and Table 2
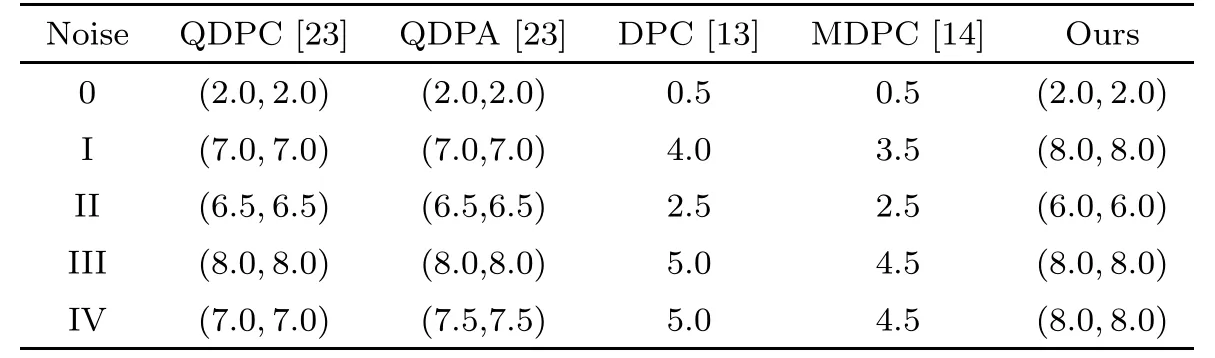
Table 11 Parameter settings for image of House in Table 1 and Table 2

Table 12 Parameter settings for image T1 in Table 1 and Table 2
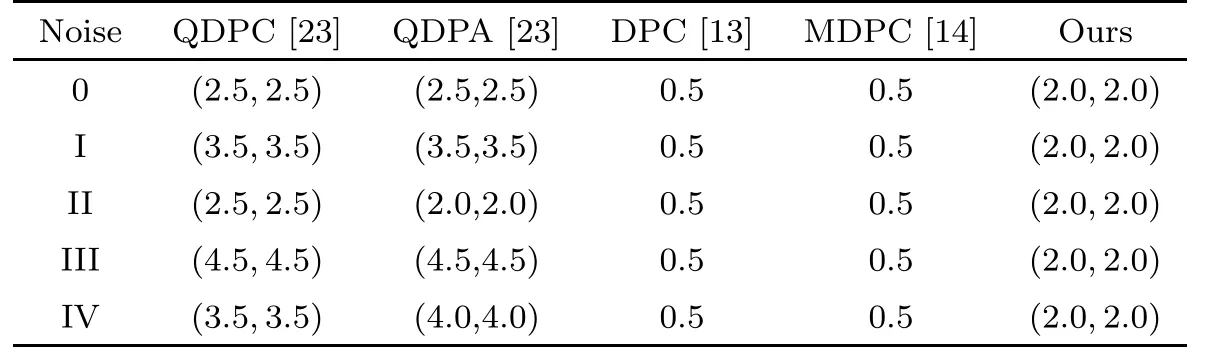
Table 13 Parameter settings for image T2 in Table 1 and Table 2

Table 14 Parameter settings for image T3 in Table 1 and Table 2
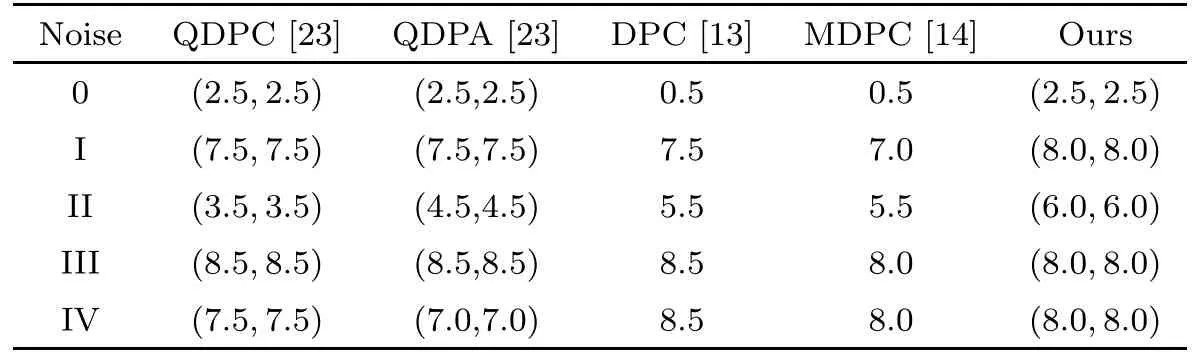
Table 15 Parameter settings for image of Cara in Table 1 and Table 2
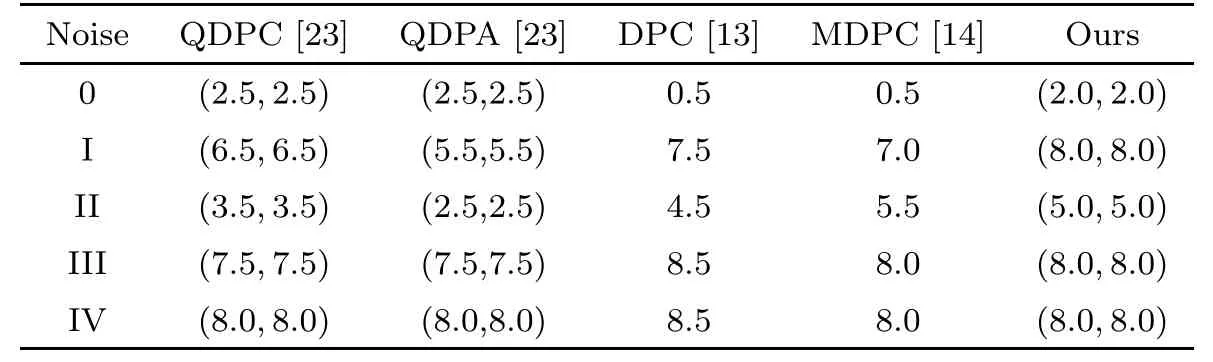
Table 16 Parameter settings for image of Frog in Table 1 and Table 2
 Acta Mathematica Scientia(English Series)2022年3期
Acta Mathematica Scientia(English Series)2022年3期
- Acta Mathematica Scientia(English Series)的其它文章
- CONTINUOUS SELECTIONS OF THE SET-VALUED METRIC GENERALIZED INVERSE IN 2-STRICTLY CONVEX BANACH SPACES*
- EXISTENCE RESULTS FOR SINGULAR FRACTIONAL p-KIRCHHOFF PROBLEMS*
- BOUNDS FOR MULTILINEAR OPERATORS UNDER AN INTEGRAL TYPE CONDITION ON MORREY SPACES*
- LEARNING RATES OF KERNEL-BASED ROBUST CLASSIFICATION*
- A COMPACTNESS THEOREM FOR STABLE FLAT SL (2,C) CONNECTIONS ON 3-FOLDS*
- CONTROL STRATEGIES FOR A TUMOR-IMMUNE SYSTEM WITH IMPULSIVE DRUG DELIVERY UNDER A RANDOM ENVIRONMENT*
