CONTINUOUS SELECTIONS OF THE SET-VALUED METRIC GENERALIZED INVERSE IN 2-STRICTLY CONVEX BANACH SPACES*

Shaoqiang SHANG (商绍强)

College of Mathematical Sciences，Harbin Engineering University，Harbin 150001，China

E-mail:sqshang@163.com

Abstract In this paper，we prove that if X is an almost convex and 2-strictly convex space，linear operator T:X→Y is bounded，N (T) is an approximative compact Chebyshev subspace of X and R (T) is a 3-Chebyshev hyperplane，then there exists a homogeneous selection Tσ of T∂ such that continuous points of Tσ and T∂ are dense on Y.

Key words Continuous selection;3-Chebyshev hyperplane;set-valued metric generalized inverses;2-strictly convex space

1 Introduction

LetXdenote a real Banach space with unit ballB(X) and unit sphereS(X).LetX*denote the dual space of Banach spaceXand letAf={x∈S(X):f(x)=1=‖f‖}.Let int (A) denote the interior ofAand diam (A) denote the diameter ofA，whereAis a subset ofX.LetTdenote a linear bounded operator fromXintoY.LetN(T) andR(T) denote the null space and the range ofT，respectively.LetHbe a subspace ofX.Then the metric projection operatorPH:X→His defined by

LetπHdenote a selection forPH.It is well known thatHis said to be proximinal ifPH(x)Ø wheneverx∈X.Moreover，subspace spaceHis said to be a Chebyshev subspace ifPH(x) is a singleton wheneverx∈X.Lety0∈Yandx0∈X.If

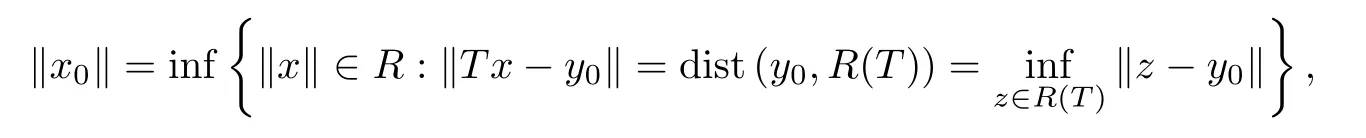
then the pointx0is said to be a best approximative solution of the equationTx=y0(see[5]).Define the set

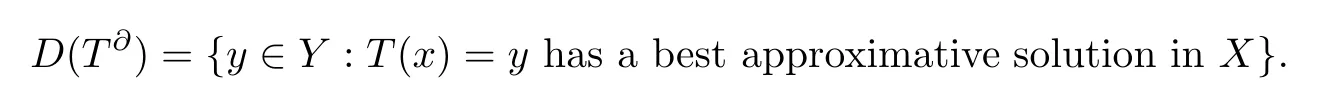
Then the set-valued mappingT∂:D(T∂)→2Xis said to be the set-valued metric generalized inverse ofT(see[5])，where

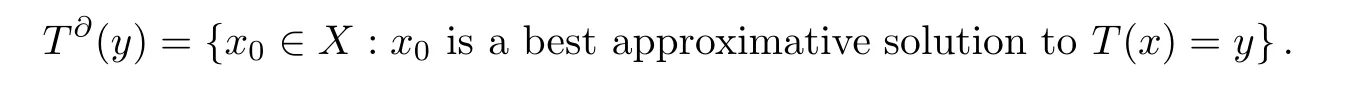
In 1974，Nashed and Votruba gave the definition of the set-valued metric generalized inverse and further pointed out that the continuous selection of the set-valued metric generalized inverse is worth studying (see[5]).In 2019，Shaoqiang Shang and Yunan Cui proved the following theorem:

Theorem 1.1(See[8]) Let Banach spaceXandYbe approximatively compact，letT:X→Ybe bounded，letN(T) be Chebyshev and letR(T) be 2-Chebyshev.Then the following statements are equivalent:

(1) the pointy0is a continuous point ofT∂;

(2) for everyz∈T∂(y0)，there exists a selectionTσofT∂such thatTσ(y0)=zandy0is a continuous point ofTσ;

(3) the functiong∂is continuous at pointy0andTT∂is lower semicontinuous at pointy0，where

The continuous selection of the set-valued metric generalized inverse has great depth and breadth，hence continuous selection has attracted the attention of a large number of mathematicians.However，since the continuous selection of generalized inverses is a very difficult problem，the research results have relatively few in this field.One of the difficulties in the study of the set-valued metric generalized inverse is that the development of geometric theory in Banach space is incomplete，and this affects the study of the set-valued metric generalized inverse.In order to further study the generalized inverse，Shaoqiang Shang and Yunan Cui gave the definition of almost convex space.

Definition 1.2(See[1]) A Banach spaceXis said to be almost convex iffn∈S(X*)，‖xn‖→1，fn(xn)→1 and the diameter ofAfnis greater than zero for alln∈N，so dist (xn，Afn)→0 asn→∞.

Using almost convex space，Shaoqiang Shang and Yunan Cui studied continuous selection of the generalized inverses and gave the following theorem:

Theorem 1.3(See[1]) LetXbe an almost convex and 2-strictly convex space，letT:X→Ybe a bounded linear operator，letN(T) be an approximative compact Chebyshev subspace ofXand letR(T) be a 2-Chebyshev hyperplane.Then there exists a homogeneous selectionTσofT∂such that continuous points ofTσandT∂are dense onY.

In Theorem 1.2，we require thatR(T) is a 2-Chebyshev hyperplane ofY.It is well known that 2-Chebyshev space is an extension of the Chebyshev space.Furthermore，we have the concept ofk-Chebyshev space.

Definition 1.4(See[11]) A subspaceHis called ak-Chebyshev subspace ofXifPH(x)Ø and dim (span{x-PH(x)})≤kwheneverx∈X.Moreover，ifk-Chebyshev subspaceHis a hyperplane ofX，thenHis called ak-Chebyshev hyperplane ofX.

It is well known thatMis a 1-Chebyshev subspace ofXif and only ifMis a Chebyshev subspace ofX.Moreover，it is well known that

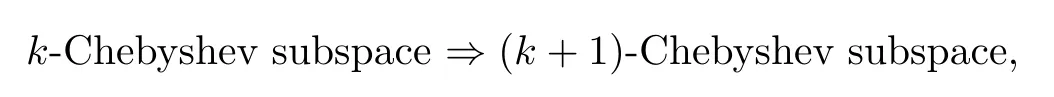
and (k+1)-Chebyshev subspace is not necessarilyk-Chebyshev subspace.Moreover，ifR(T) is a 3-Chebyshev hyperplane，then the method of proof of Theorem 1.3 is completely invalid.Naturally，therefore，we have to ask:ifR(T) is 3-Chebyshev，is Theorem 1.3 true?In this paper，we prove that ifXis an almost convex and 2-strictly convex space，linear operatorT:X→Yis bounded，N(T) is an approximative compact Chebyshev subspace ofXandR(T) is a 3-Chebyshev hyperplane，then there exists a homogeneous selectionTσofT∂such that continuous points ofTσandT∂are dense onY.Moreover，ifR(T) is a 2-Chebyshev hyperplane ofY，then (1) continuous points ofT∂are dense onwhereG0={y∈Y:diamT∂(y)=0}andT∂are continuous on(2) there exists a homogeneous selectionTσofT∂such that continuous points ofTσare dense onand are continuous onOther results of generalized inverses are shown in[2–4]and[6–8].We next give some definitions that we will use later.

Definition 1.5(See[9]) A pointx0is called a continuous point ofG:X→2Yifx0is an upper semicontinuous point and is a lower semicontinuous point ofG.

Definition 1.6(See[11]) A closed subspaceMofXis called approximatively compact if⊂Mhas a subsequence of convergence wheneverx∈Xand ‖x-yn‖→dist (x，M).

Definition 1.7(See[12]) A Banach spaceXis called 2-strictly convex ifx1，x2，x3are linearly dependent whenever{x1，x2，x3}⊂S(X) and ‖x1+x2+x3‖=3.

2 Main Theorems

Theorem 2.1LetXbe an almost convex and 2-strictly convex space，letT:X→Ybe a bounded linear operator，letN(T) be an approximative compact Chebyshev subspace ofXand letR(T) be a 3-Chebyshev hyperplane.Then there exists a homogeneous selectionTσofT∂such that continuous points ofTσandT∂are dense onY.

In order to get the theorem，we give some lemmas.

Lemma 2.2Suppose thatXis a Banach space，thatAis a convex subset ofX，that[x1，x2]⊂Aand that[x1，x2]∩intAØ.Then (x1，x2)⊂intA，where (x1，x2)={tx1+(1-t)x2:t∈(0，1)}and[x1，x2]={tx1+(1-t)x2:t∈[0，1]}.

ProofIt is easy to see that the Lemma is true，which completes the proof. □

Lemma 2.3Suppose thatXis 2-strictly convex，thatT:X→Yis a bounded linear operator，that subspaceN(T) ofXis a proximinal and thatR(T) is ak-Chebyshev subspace ofY.Then for anyy∈Y，T∂(y) is a line segment.

ProofSinceR(T) is ak-Chebyshev subspace ofY，we get thatPR (T)(y) is compact for everyy∈Y.Define the linear operatorwhere[x]∈X/N(T) andx∈X.SinceR(T) is ak-Chebyshev subspace ofY，we obtain thatR(T) is closed.SinceTis a bounded linear operator，by the definition ofwe obtain thatis bounded.Therefore，by the inverse operator Theorem，we get thatis bounded.Let⊂PR (T)(y) such that

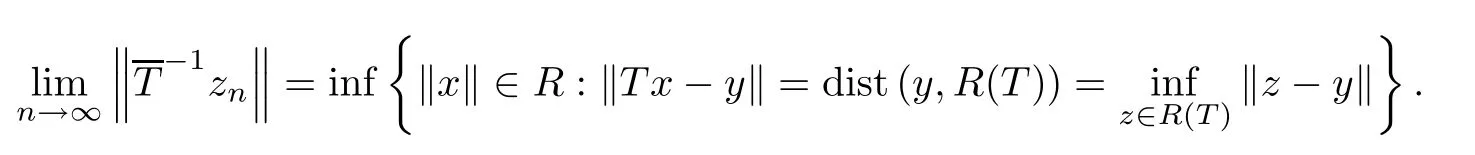
SincePR (T)(y) is compact，we can assume thatzn→z0asn→∞.Then there exists a pointu0∈Xsuch thatTu0=z0.Hence we get thatu0-PN (T)(u0)⊂T∂(y).This implies thatT∂(y)Ø for everyy∈Y.Suppose that there exists a pointy0∈Ysuch thatT∂(y0) is not a line segment.Then there exists a set{x1，x2，x3}⊂T∂(y0) such that co{x1，x2，x3}is not a line segment.Moreover，we may assume thatT∂(y0)⊂S(X).Therefore，by the convexity ofT∂(y0)，we get that

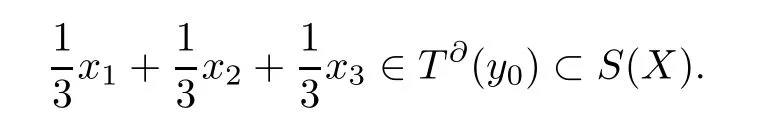
Therefore，by the Hahn-Banach Theorem and the above formula，there exists a functional∈S(X*) such that

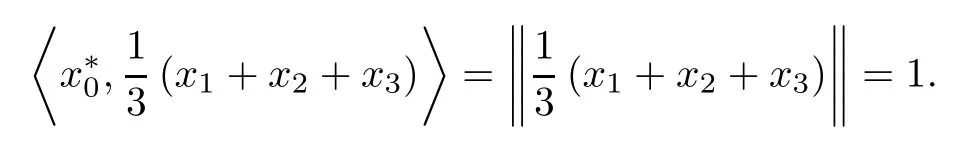
This implies that ‖x1+x2+x3‖=‖x1‖+‖x2‖+‖x3‖=3 andSinceXis 2-strictly convex，we get thatx1，x2，x3are linearly dependent.Hence we may assume thatx3=t1x1+t2x2.Then.This implies thatt1+t2=1.Hence we havex3∈{λx1+(1-λ)x2:λ∈R}，which contradicts the fact co{x1，x2，x3}is not a line segment.Hence we get thatT∂(y) is a line segment for anyy∈Y，which completes the proof. □

We next will prove Theorem 2.1.

ProofSinceN(T) is an approximative compact Chebyshev subspace ofX，we get thatN(T) is proximinal.SinceXis a 2-strictly convex space andR(T) is a 3-Chebyshev hyperplane，by Lemma 2.3，we get that for everyy∈Y，T∂(y) is a line segment.We divide the proof into five steps.

Step 1Let us first prove thatT∂is upper semicontinuous onY.Suppose thatT∂is not upper semicontinuous at pointy0.Then there exists an open setW⊃T∂(y0) and two sequences，xn∈T∂(yn) and ‖yn-y0‖→0 asn→∞.Define the bounded linear operatorwhere[x]∈X/N(T) andx∈X.Then we obtain thatis a bounded linear operator.SinceT∂(y) is a line segment for everyy∈Y，letT∂(yn)=[x(1，n)，x(2，n)]for everyn∈N.SinceN(T) is an approximative compact Chebyshev subspace ofX，by the proof of Theorem 5 of[1]，we get the following formulas:

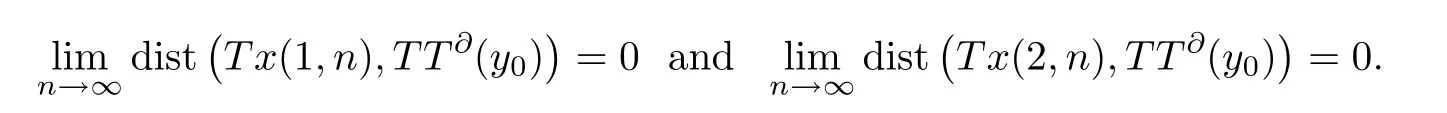
Moreover，by the proof of Theorem 5 of[1]，we get a contradiction.Hence we get thatT∂is upper semicontinuous onY.

Step 2SinceR(T) is a 3-Chebyshev hyperplane ofY，we get thatR(T) is proximinal.Therefore，by the proof of Theorem 5 of[1]，there exists a functionalf∈S(X*) such that

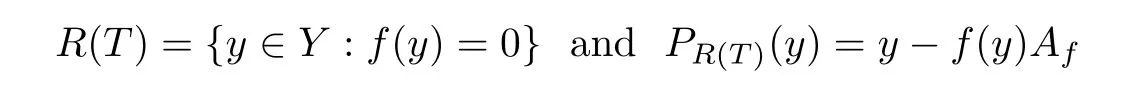
for ally∈Y.Pick a pointy0/∈R(T).Then we get thatf(y0)0.SinceR(T) is a 3-Chebyshev hyperplane ofY，by the formulaPR (T)(y)=y-f(y)Af，we have

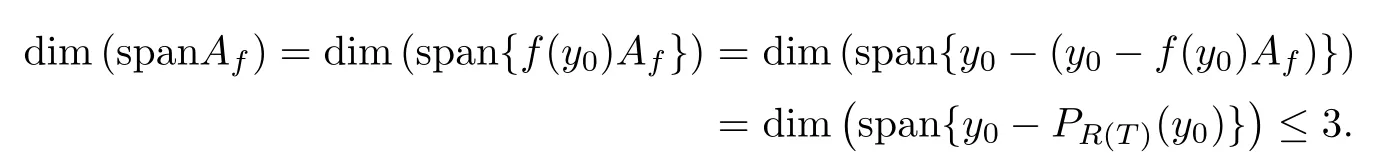
Hence，if dim (spanAf)=1，then the setT∂(y) is a singleton for everyy∈Y.SinceT∂is upper semicontinuous onY，we get thatT∂is continuous onY.Moreover，if dim (spanAf)=2，thenR(T) is a 2-Chebyshev hyperplane ofY.Therefore，by Theorem 5 of[1]，we get that there exists a homogeneous selectionTσofT∂such that continuous points ofTσandT∂are dense onY.Hence we may assume，without loss of generality，that dim (spanAf)=3.Since dim (spanAf)=3，there exists a set{z1，z2，z3}⊂Afsuch thatz1，z2，z3are linearly independent.Therefore，by the formula dim (spanAf)=3，we get thatHf={t1z1+t2z2+t3z3∈X:t1+t2+t3=1}⊃Afis a hyperplane of three-dimensional spaceX0=span{z1，z2，z3}.Pick a point

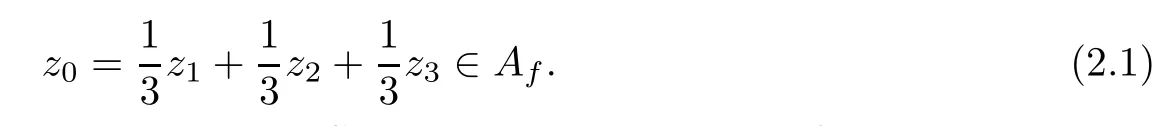
Then，byAf⊂Hf，we haveAf-z0⊂Hf-z0.SinceHfis a hyperplane of three-dimensional space，we obtain thatHf-z0=span{Af-z0}is a two-dimensional space.Sincez1，z2，z3are linearly independent，we get thatAf-z0is a convex subset ofHf-z0and that int (Af-z0)Ø.

Step 3DefineG0={y∈Y:diamT∂(y)=0}.Letv0∈YG0.Then there exists a real numberr∈(0，+∞) such thatB(v0，r)⊂YG0，whereB(v0，r)={z∈X:‖z-v0‖≤r}.Define the set

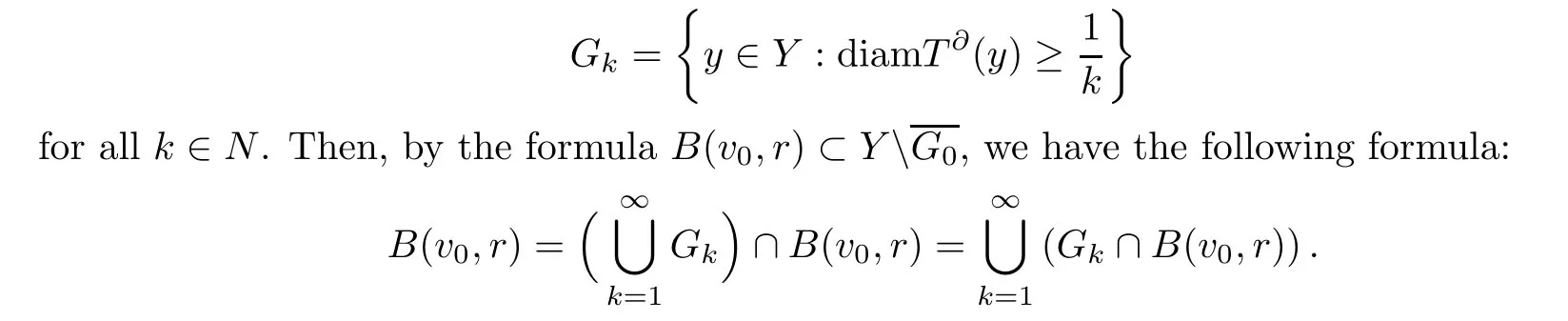
We claim thatGkis closed for everyk∈N.In fact，let⊂Gkand ‖yi-z0‖→0 asi→∞.LetT∂(yi)=[u(1，i)，u(2，i)]for everyi∈N.Then，from the proof of Step 1，we may assume that dist（Tu(1，i)，TT∂(z0)）→0 asi→∞.Hence we may assume that there exists a pointu(1，0)∈T∂(z0) such thatTu(1，i)→Tu(1，0)∈TT∂(z0).Sinceis a bounded linear operator，there exists a sequence⊂N(T) such that ‖u(1，i)+zi-u(1，0)‖→0 asi→∞.Sinceis a bounded linear operator，byu(1，i)∈T∂(zi) andu(1，0)∈T∂(z0)，we get that ‖u(1，i)‖→‖u(1，0)‖ asi→∞.Therefore，by the formulau(1，0)∈T∂(z0)，we have

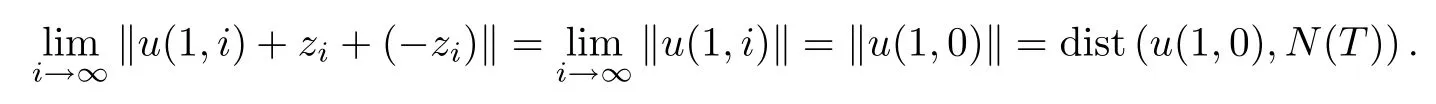
SinceN(T) is an approximative compact Chebyshev subspace ofX，by the formula ‖u(1，i)+zi-u(1，0)‖→0，we may assume thatis a Cauchy sequence.Hence we obtain thatis a Cauchy sequence.Let ‖u(1，i)-u0(1，0)‖→0 asi→∞.Then，by the formula ‖u(1，i)‖→‖u(1，0)‖，we get that ‖u(1，0)‖=‖u0(1，0)‖.Moreover，byTu(1，i)→Tu(1，0)∈TT∂(z0) and ‖u(1，i)-u0(1，0)‖→0，we haveTu0(1，0)=Tu(1，0)∈TT∂(z0).Therefore，byu(1，0)∈T∂(z0) and ‖u(1，0)‖=‖u0(1，0)‖，we haveu0(1，0)∈T∂(z0).Similarly，we get thatu(2，i)→u0(2，0)∈T∂(z0) asi→∞.This implies that

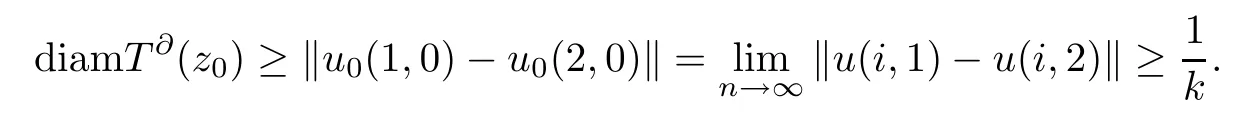
Thenz0∈Gk.This implies thatGkis closed for allk∈N.Hence we get thatGk∩B(v0，r) is closed for allk∈N.Since closed ballB(v0，r) is a complete metric space，by the Baire Theorem of categories，there exists a natural numberk0such thatGk0∩B(v0，r) has an interior point ofGk0∩B(v0，r).Hence there exists a pointy0∈Gk0∩B(v0，r) and a real numberδ∈(0，+∞) such that the pointy0is an interior point ofGk0∩B(v0，r) andB(y0，δ)∩R(T)=Ø.Letε＞0.Sincey0is an interior point ofGk0∩B(v0，r)，there existsd∈(0，min{ε，δ/2}) such that

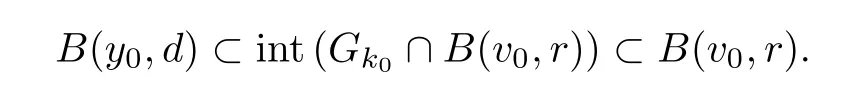
Moreover，sinceB(y0，δ)∩R(T)=Ø andd∈(0，min{ε，δ/2})，we get thatB(y0，d)∩R(T)=Ø.

Step 4We will prove that continuous points ofT∂are dense onY.In fact，sinceT∂is upper semicontinuous onY，we obtain thatT∂is continuous at every point ofG0={y∈Y:diamT∂(y)=0}.Therefore，by the proof shown in Step 3，we just need to prove thatT∂has a lower semicontinuous point onB(y0，d).Moreover，by the proof shown in Step 2，we know that there exists a functionalf∈S(X*) such that

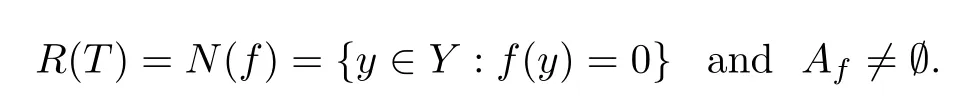
SincePR (T)(y)=y-f(y)Affor everyy∈Y，we obtain that ifπR (T)(y)∈PR (T)(y)，then there exists a unique pointz∈Afsuch thatπR (T)(y)=y-f(y)zwhenevery∈YR(T).SinceT∂(y) is a line segment for everyy∈Y，we obtain thatTT∂(y) is a line segment for everyy∈Y.Hence we define a set-valued mappingF:YR(T)→2Ysuch thatF(y)=[z1，z2]⊂Af，where

for everyy∈YR(T).For clarity，we will next divide the proof into two cases.

Case IFor anyr＞0 there exists a pointy∈B(y0，r) such that (F(y)-z0)∩int (Af-z0)Ø，where the definition ofz0see formula (2.1).Hence we can assume that

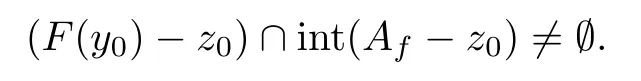
Moreover，from the proof shown in Step 3，we know that there exists a natural numberk0∈Nand a real numberd＞0 such that

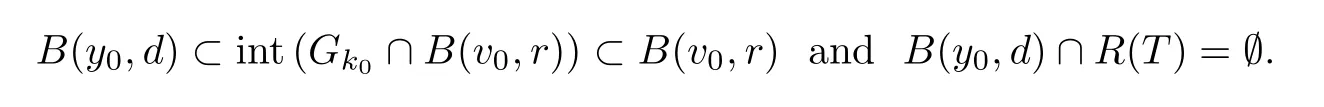
Let ‖yn-y0‖→0 asn→∞.Then we may assume，without loss of generality，thatB(y0，d/2).LetT∂(y0)=[x(1，0)，x(2，0)]andT∂(yn)=[x(1，n)，x(2，n)]for everyn∈N.Then ‖x(1，0)-x(2，0)‖≥1/k0and ‖x(1，n)-x(2，n)‖≥1/k0for alln∈N.Moreover，from the proof shown in Step 1，we can assume，without loss of generality，that

Pick a pointx0∈T∂(y0).We next will prove that there exists a pointxn∈T∂(yn) such that ‖xn-x0‖→0 asn→∞.SinceT∂is upper semicontinuous onY，we can assume，without loss of generality，thatx(1，n)→u(1，0)∈T∂(y0) andx(2，n)→u(2，0)∈T∂(y0) asn→∞.Then we get thatu(1，0)u(2，0).We claim thatTu(1，0)-Tu(2，0)0.Otherwise，we would haveu(2，0)-u(1，0)∈N(T).Hence 0∈PN (T)(u(1，0)) andu(1，0)-u(2，0)∈PN (T)(u(1，0)).SinceN(T) is an approximative compact Chebyshev subspace ofX，we get thatu(2，0)-u(1，0)=0，which is a contradiction.Therefore，by the formulasT∂(y0)=[x(1，0)，x(2，0)]andTu(1，0)-Tu(2，0)0，we get thatTx(1，0)-Tx(2，0)0.Moreover，by the formulaPR (T)(y)=y-f(y)Af，there exist two pointsz(1，0)∈Afandz(2，0)∈Afsuch that

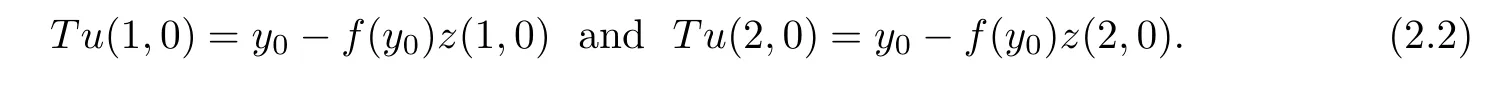
Moreover，there exist two pointsz(1，n)∈Afandz(2，n)∈Afsuch that

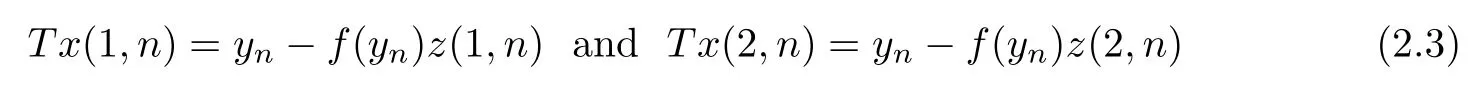
for alln∈N.SinceTx(1，n)→Tu(1，0) andTx(2，n)→Tu(2，0)，by formulas (2.2) and (2.3)，we obtain that ‖z(1，n)-z(1，0)‖→0 and ‖z(2，n)-z(2，0)‖→0 asn→∞.Moreover，by the formulasT∂(y0)=[x(1，0)，x(2，0)]andu(1，0)-u(2，0)0，we get that

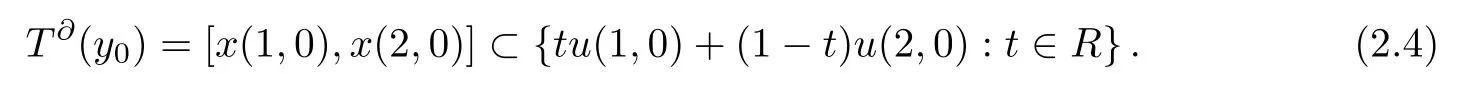
SinceTu(1，0)-Tu(2，0)0，byTx(1，n)→Tu(1，0) andTx(2，n)→Tu(2，0)，we can assume thatandx0∈[x(1，0)，x(2，0)]，by formula (2.4)，we get that

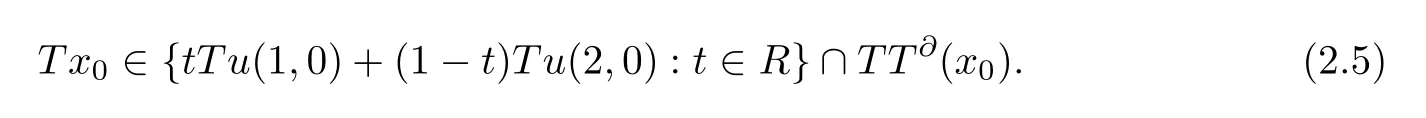
Moreover，by the formulasPR (T)(y0)=y0-f(y0)AfandTx0∈PR (T)(y0)，there exists a pointv0∈Afsuch thatTx0=y0-f(y0)v0.Therefore，by formulas (2.2) and (2.5)，we have

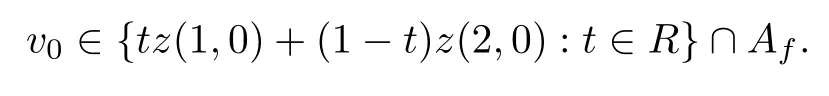
Moreover，by the definition ofF，we havev0∈F(y0).Hence there existst0∈Rsuch that

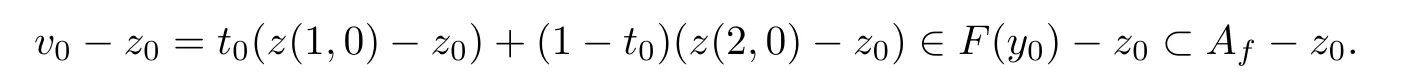
Therefore，by the formulas ‖z(1，n)-z(1，0)‖→0 and ‖z(2，n)-z(2，0)‖→0，we obtain that ‖vn-v0‖→0 asn→∞，where

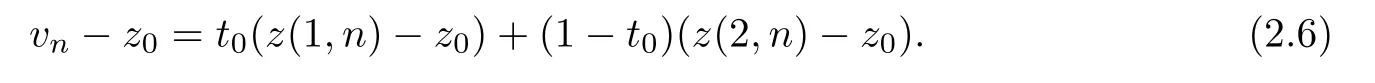
Then we get thatvn-z0∈span{Af-z0}.Sincez(1，0)-z0∈Af-z0，z(2，0)-z0∈Af-z0，z(1，n)-z0∈Af-z0andz(2，n)-z0∈Af-z0，by the convexity ofAf-z0，we have the formulas

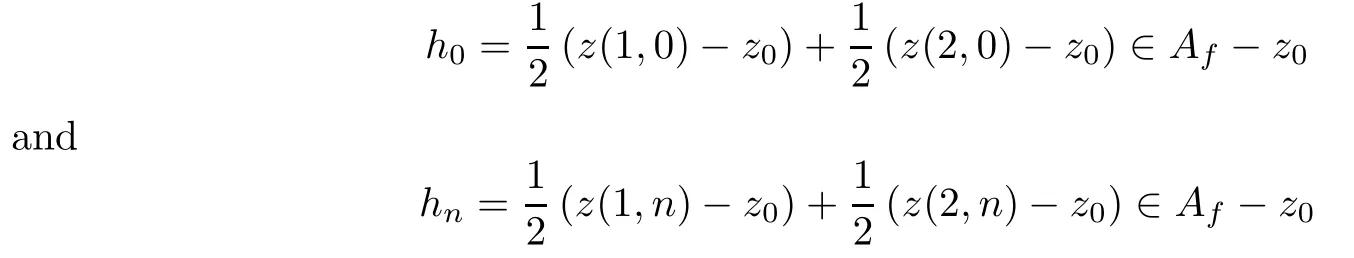
for alln∈N.Since (F(y0)-z0)∩int (Af-z0)Ø，by Lemma 2.2，we get thath0is an interior point ofAf-z0in two dimensional space span{Af-z0}.Hence there exists a real numberη∈(0，+∞) such that

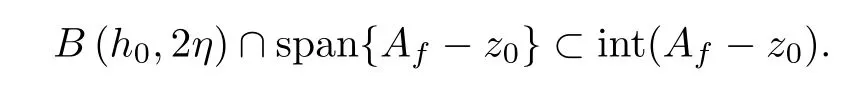
Moreover，since ‖z(1，n)-z(1，0)‖→0 and ‖z(2，n)-z(2，0)‖→0，by the above formula，we can assume that

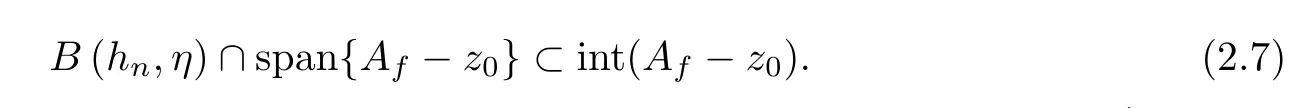
This implies thathnis an interior point ofAf-z0in two dimensional Banach space span{Afz0}.Hence the origin point is an interior point ofAf-z0-hnin two dimensional Banach space span{Af-z0}.Hence，for anyn∈N，we define the Minkowski functional

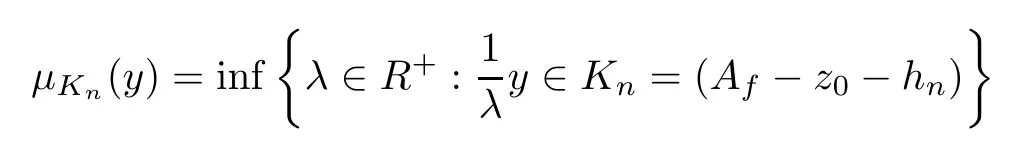
in two dimensional Banach space span{Af-z0}.Therefore，by formula (2.7) and the definition ofμKn，we have the formula

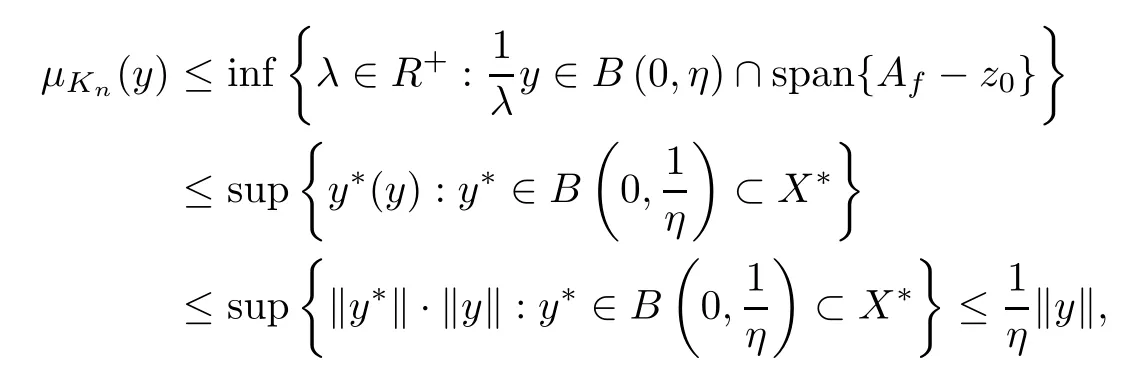
whenevery∈span{Af-z0}.Letm=1/η.Then we get that|μKn(y)|≤m‖y‖ for everyn∈N.Therefore，byv0-z0∈Af-z0，we obtain thatv0-z0-hn∈Af-z0-hn.This implies thatμKn(v0-z0-hn)≤1 for alln∈N.Sincevn-z0∈span{Af-z0}andhn∈span{Af-z0}，we obtain thatvn-z0-hn∈span{Af-z0}.Therefore，by the formulas|μKn(y)|≤m‖y‖ andvn-z0-hn∈span{Af-z0}，we have the inequalities

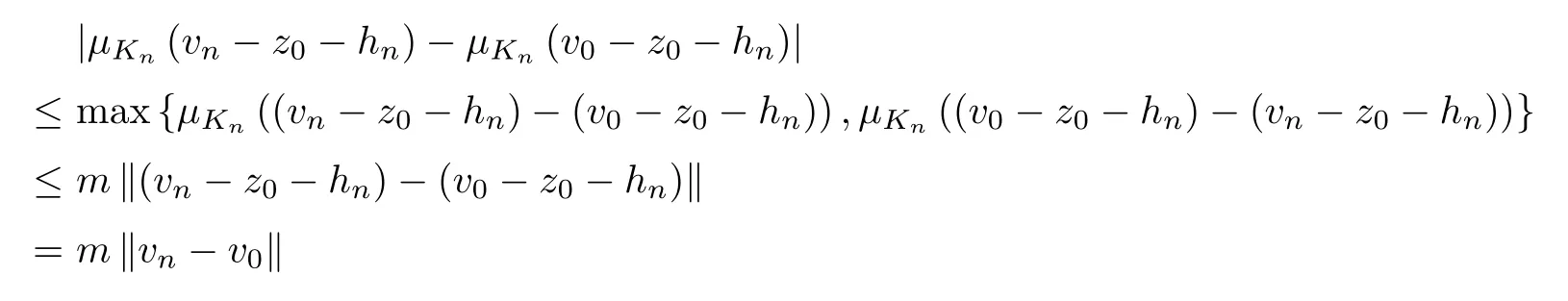
for alln∈N.Therefore，by the formulasμKn(v0-z0-hn)≤1 and ‖vn-v0‖→0，we have

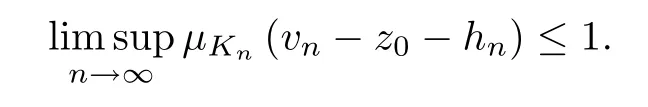
Therefore，by the above inequality，there exists a sequence⊂[0，1]such that

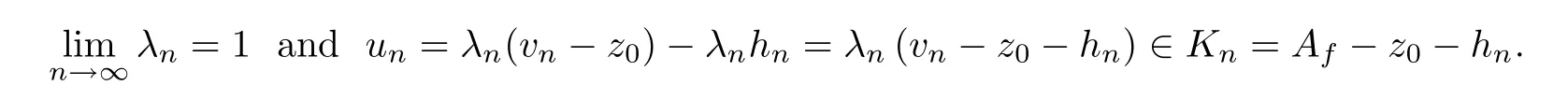
Moreover，it is easy to see that

for alln∈N.Sinceun∈Af-z0-hn，by the above formula，we have the formula

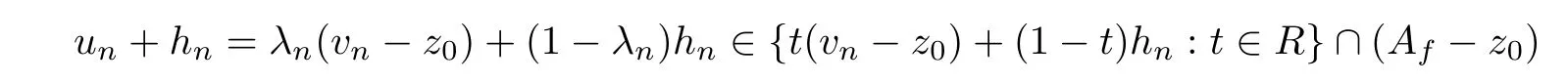
for alln∈N.Sincevn-z0=t0(z(1，n)-z0)+(1-t0)(z(2，n)-z0) andhn=(z(1，n)-z0)/2+(z(2，n)-z0)/2，by the above formula，we have the formula

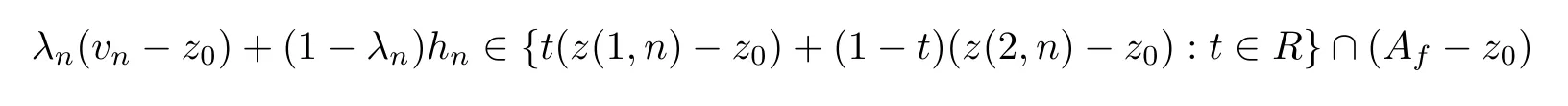
for alln∈N.Therefore，by the above formula，we have the formula

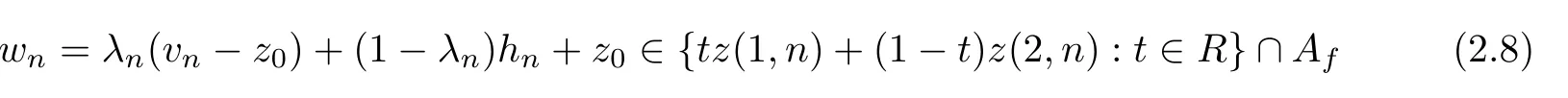
for alln∈N.Therefore，by the formulasλn→1 and ‖vn-v0‖→0，we get that ‖wn-v0‖→0 asn→∞.Therefore，by the formulas ‖yn-y0‖→0 and ‖wn-v0‖→0，we have

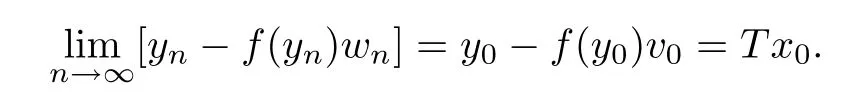
Moreover，by the formulaPR (T)(yn)=yn-f(yn)Af，we obtain thatyn-f(yn)wn∈PR (T)(yn) for alln∈N.Therefore，by formulas (2.3) and (2.8)，we have

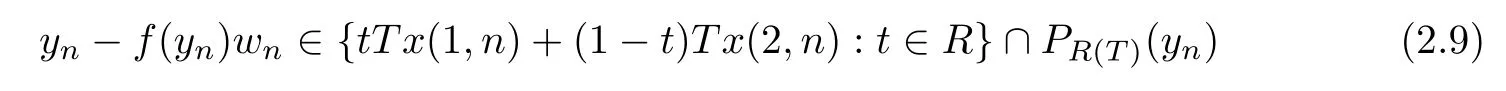
for alln∈N.SinceT∂(yn)=[x(1，n)，x(2，n)]for alln∈N，it is easy to see that (x(1，n)+x(2，n))/2∈T∂(yn) for alln∈N.Therefore，by the formulasx(1，n)∈T∂(yn) andx(2，n)∈T∂(yn)，we have the formula

for alln∈N.Therefore，by the Hahn-Banach Theorem，there exists a functionalfn∈S(X*) such that

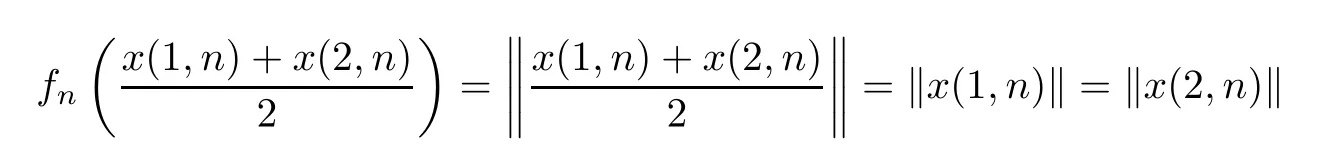
for alln∈N.Therefore，by the formulasx(1，n)→u(1，0)∈T∂(y0) andx(2，n)→u(2，0)∈T∂(y0)，we have the following formula:

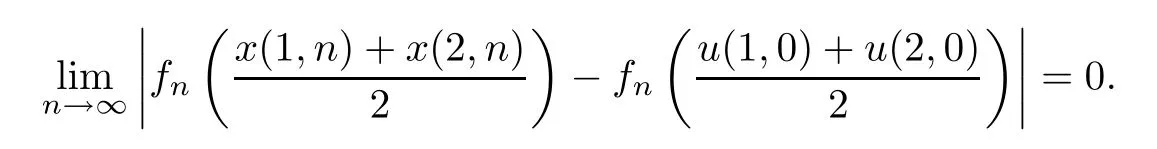
Therefore，by the above formula，we have the formula

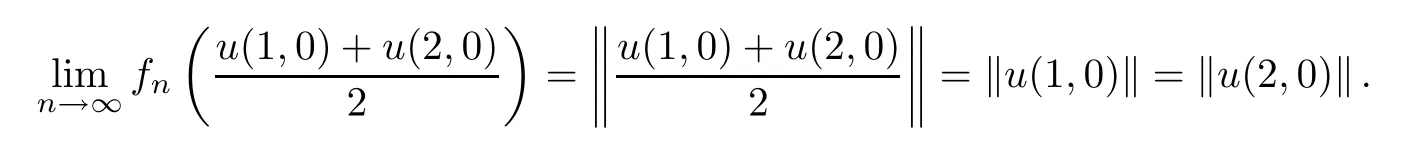
Moreover，we can assume thatT∂(y0)⊂S(X).Therefore，by the formulasu(1，0)-u(2，0)0 andx0∈{tu(1，0)+(1-t)u(2，0):t∈R}，we get thatfn(x0)→1 asn→∞.Moreover，by the formulaT∂(y0)⊂S(X)，we get that ‖x(1，n)‖→‖u(1，0)‖=1 asn→∞.SinceXis an almost convex and 2-strictly convex space，we get that

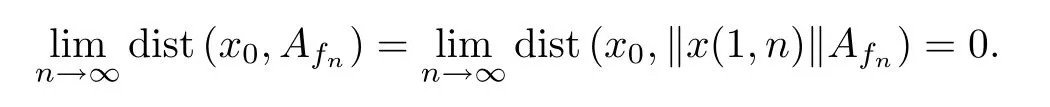
Therefore，by the formula ‖x(1，n)‖Afn⊂{tx(1，n)+(1-t)x(2，n):t∈R}，there exists a point

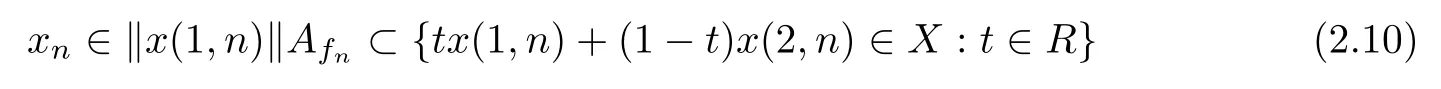
such thatxn→x0and ‖xn‖=‖x(1，n)‖ for everyn∈N.Hence，ifTxn∈PR (T)(yn) for everyn∈N，we obtain thatxn∈T∂(yn).Otherwise，we can assume thatTxnPR (T)(yn) for everyn∈N.Then，by formula (2.10) and the definition ofyn-f(yn)wn，there exist two sequences⊂Rsuch thatxn=λnx(1，n)+(1-λn)x(2，n) and

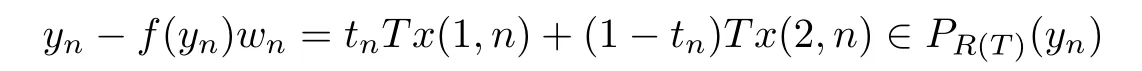
for everyn∈N.Therefore，by the formula ‖xn-x0‖→0，we get that ‖Txn-Tx0‖→0 asn→∞.Therefore，by formula (2.9) and ‖yn-f(yn)wn-Tx0‖→0，we get that

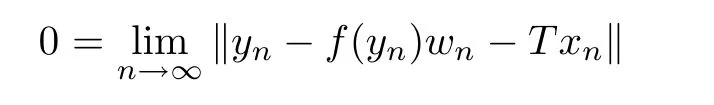
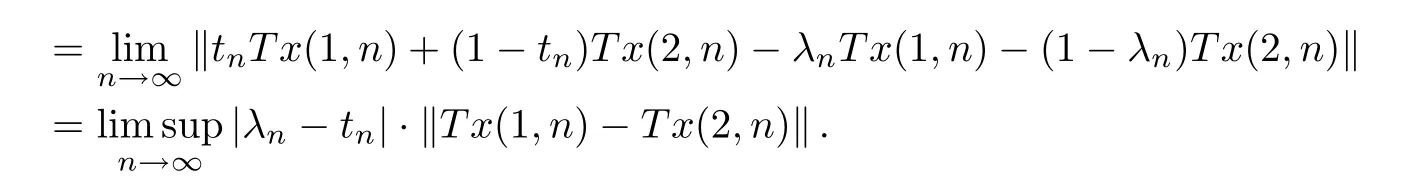
Therefore，by formula liminfn→∞‖Tx(1，n)-Tx(2，n)‖＞0，we haveλn-tn→0 asn→∞.Moreover，by the formulasTxnPR (T)(yn) andyn-f(yn)wn∈PR (T)(yn)，we may assume thatyn-f(yn)wn∈[Txn，Tx(1，n)]for everyn∈N.Define the sequence{en}∞n=1⊂X，whereen=tnx(1，n)+(1-tn)x(2，n) for alln∈N.Then，by the formulasλn-tn→0 andxn=λnx(1，n)+(1-λn)x(2，n)，we have ‖en-xn‖→0 asn→∞.This implies that ‖en-x0‖→0 asn→∞.Therefore，byTen=yn-f(yn)wn∈PR (T)(yn) andyn-f(yn)wn∈[Txn，Tx(1，n)]，we get thaten∈[xn，x(1，n)]for alln∈N.Then，byTen∈PR (T)(yn)，we haveen∈T∂(yn) for alln∈N.

Case IIThere exists a real numberr＞0 such that (F(y)-z0)∩int (Af-z0)=Ø for anyy∈B(y0，r).Pick a pointx0∈T∂(y0) and letT∂(yn)=[x(1，n)，x(2，n)]and ‖yn-y0‖→0 asn→∞.Then，from the previous proof，we have that

Moreover，by Step 1，we get thatT∂is upper semicontinuous onY.Hence we may assume，without loss of generality，thatx(1，n)→u(1，0)∈T∂(y0) andx(2，n)→u(2，0)∈T∂(y0).Moreover，by the previous proof，we obtain thatTu(1，0)Tu(2，0).Therefore，by the formulaPR (T)(y)=y-f(y)Af，there exist two pointsz(1，0)∈Afandz(2，0)∈Afsuch that

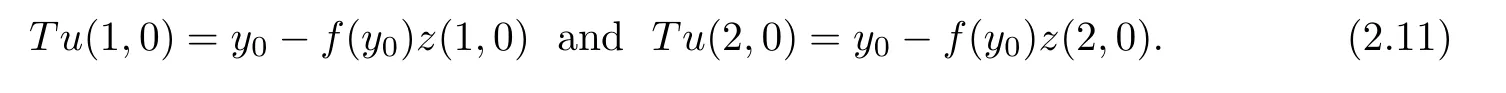
Moreover，there exist two pointsz(1，n)∈Afandz(2，n)∈Afsuch that

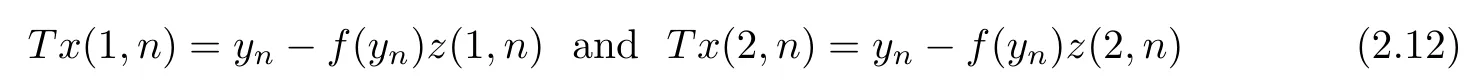
for everyn∈N.Hencez(1，n)→z(1，0) andz(2，n)→z(2，0) asn→∞.Thenz(1，n)-z0→z(1，0)-z0andz(2，n)-z0→z(2，0)-z0asn→∞.Since there exists a real numberr＞0 such that (F(y)-z0)∩int (Af-z0)=Ø for anyy∈B(y0，r)，by Lemma 2.2，we get that

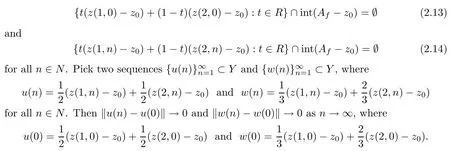
Sincez(1，n)-z0∈Af-z0andz(2，n)-z0∈Af-z0，we get thatu(n)∈Af-z0andw(n)∈Af-z0.Therefore，by formula (2.14)，we get thatu(n)int (Af-z0) andw(n)int (Af-z0) for everyn∈N.Pick a pointv(0)∈int (Af-z0).Then，by the formulau(0)int (Af-z0)，we get thatv(1)=2u(0)-v(0)Af-z0.In fact，suppose thatv(1)=2u(0)-v(0)∈Af-z0.Then，by Lemma 2.2，we have that

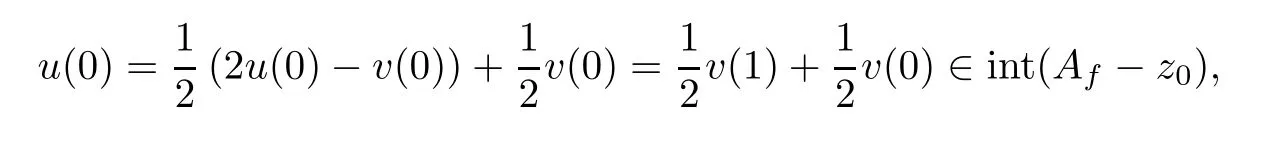
which is a contradiction.Since span{Af-z0}is a two dimensional space，it is easy to see thatu(0) andw(0) are two interior points ofG，where

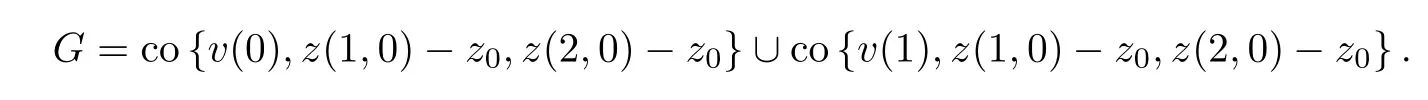
Therefore，by formulas ‖u(n)-u(0)‖→0 and ‖w(n)-w(0)‖→0，we can assume thatu(n)∈Gandw(n)∈G.Sincev(0)∈int (Af-z0) andv(1)=2u(0)-v(0)Af-z0，by formula (2.13)，we have the following formula:

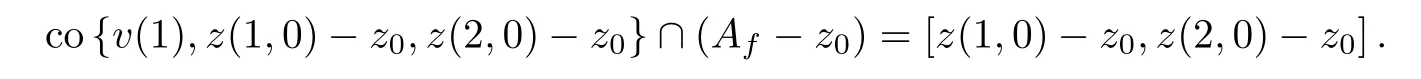
Sinceu(n)∈Af-z0，u(n)∈G，w(n)∈Af-z0andw(n)∈G，by the definition ofGand the above formula，it is easy to see that

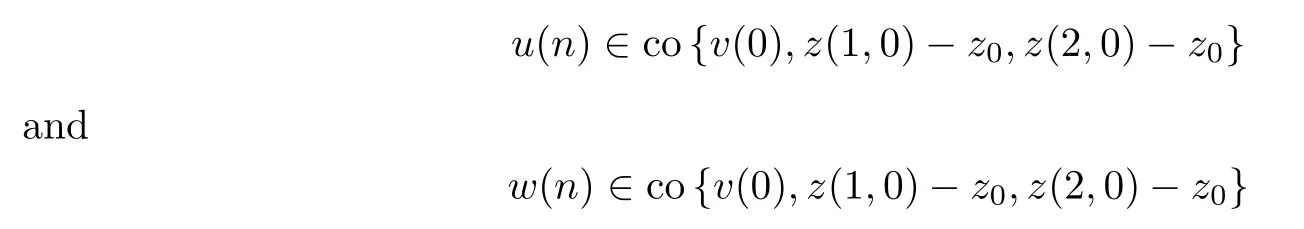
for alln∈N.Moreover，sincev(0)∈int (Af-z0)，by Lemma 2.2 and formula (2.13)，we have

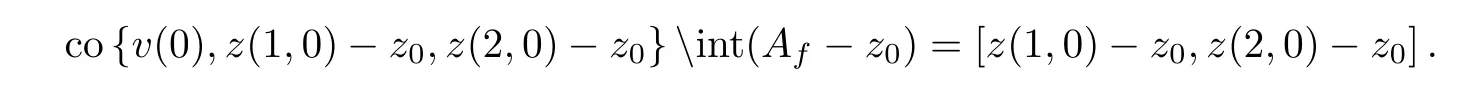
Therefore，by the formulasu(n)int (Af-z0) andw(n)int (Af-z0)，we have

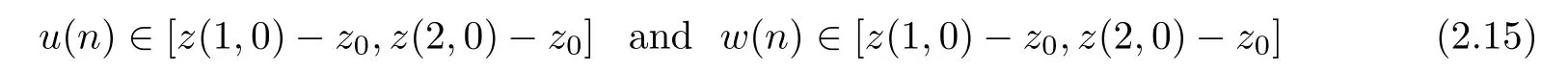
for alln∈N.Moreover，sinceTu(1，0)Tu(2，0)，by the definitions ofu(0) andw(0)，we get that ‖u(0)-w(0)‖＞0.Therefore，by the formulas ‖u(n)-u(0)‖→0 and ‖w(n)-w(0)‖→0，we can assume that 2‖u(n)-w(n)‖＞‖u(0)-w(0)‖＞0 for alln∈N.Therefore，by formula (2.15)，we have the equation

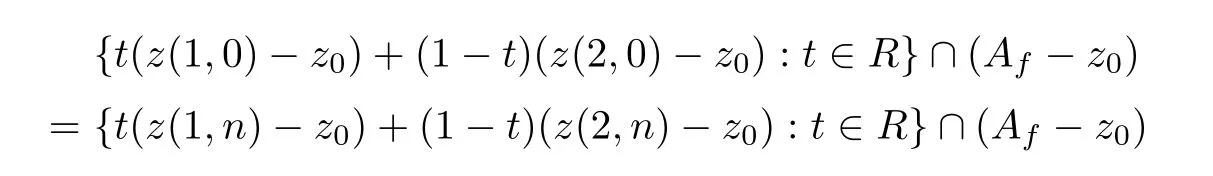
for alln∈N.Therefore，by the above equation，we get that

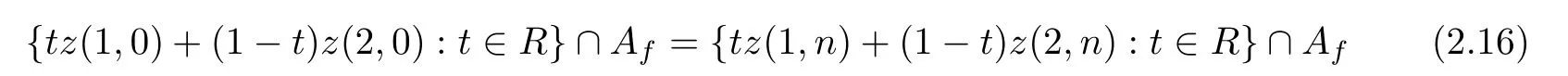
for alln∈N.SinceTu(1，0)-Tu(2，0)0，by the formulasTx0∈TT∂(y0)⊂PR (T)(y0) and ‖yn-y0‖→0，there exists a pointw0∈Afsuch that

Therefore，by the above formula and formula (2.11)，there existst0∈Rsuch that

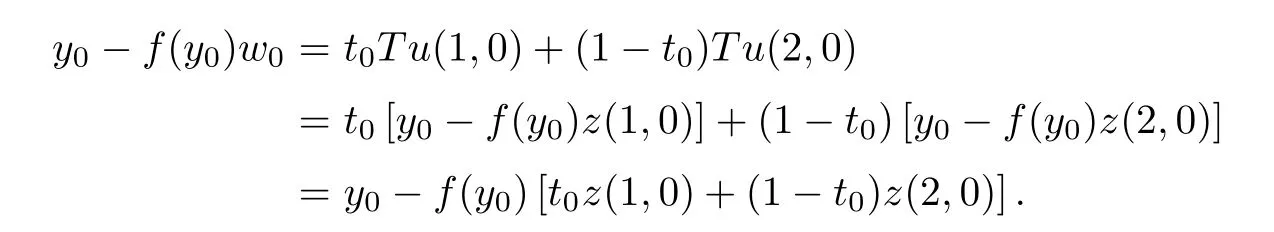
Therefore，by the formulay0/∈R(T)=N(f)，we havew0=t0z(1，0)+(1-t0)z(2，0).Therefore，by formula (2.16)，there exists a sequence⊂Rsuch thatw0=tnz(1，n)+(1-tn)z(2，n).Therefore，by formula (2.12)，we have the formula

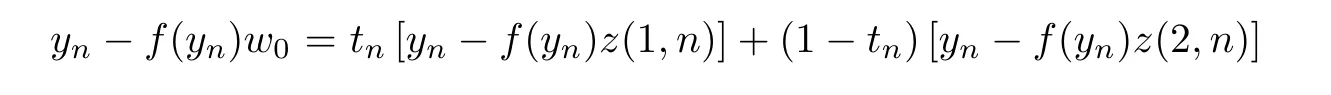
for everyn∈N.Repeating the proof used in Case I，by formulas (2.11)-(2.12) and (2.16)，there exists a pointxn∈T∂(yn) such that ‖xn-x0‖→0 asn→∞.

Therefore，by Cases I and II，we get that lower-semicontinuous points ofT∂are dense onY.SinceT∂is upper semicontinuous onY，we get that continuous points ofT∂are dense onY.

Step 5LetT∂(y)=[x(y，1)，x(y，2)]for ally∈Y.Then we define a mappingTσ:Y→X，where

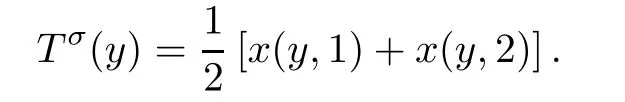
Therefore，by the proof of Theorem 5 of[1]，we get that continuous points ofTσare dense onY.We next will prove thatTσ:Y→Xis homogeneous.In fact，letv∈Yandλ∈R.Pick a pointu∈T∂(v).Then

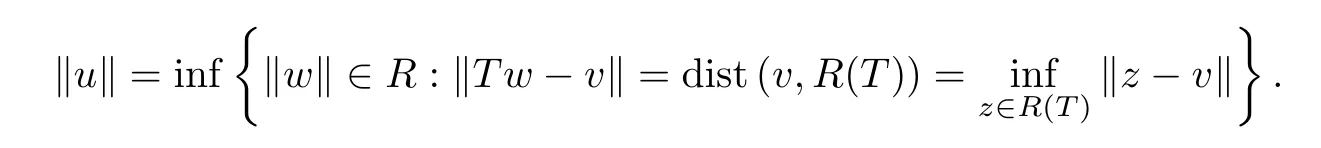
SincePR (T)(λv)=λPR (T)(v)，by the above formula，we get that

HenceλT∂(v)⊂T∂(λv).Similarly，we get thatT∂(λv)⊂λT∂(v).Hence we get thatλT∂(y)=T∂(λy) for everyλ∈Randy∈Y.Therefore，by the definition ofTσandλT∂(y)=T∂(λy)，we get thatTσ:Y→Xis a homogeneous mapping，which completes the proof. □

Under the conditions of Theorem 2.1，it is easy to see that the setG0={y∈Y:diamT∂(y)=0}is nonempty.In general，the setG={y∈Y:diamT∂(y)＞0}is nonempty.To illustrate this problem，we give an example.

Example 2.4LetX=(R2，‖·‖0) andY=(R3，‖·‖1)，where ‖(x，y)‖0=max{|x|，|y|}and ‖(x，y，z)‖1=max{|x|，|y|，|z|}.LetT:X→Ybe a bounded linear operator，whereT(x，y)=(x，y，0).ThenXis 2-strictly convex.Moreover，by Theorem 4 of[1]，we get thatXis an almost convex space.It is easy to see thatR(T) is a 3-Chebyshev hyperplane ofY.Pick a point (0，3，1)∈Y.Then it is easy to see that

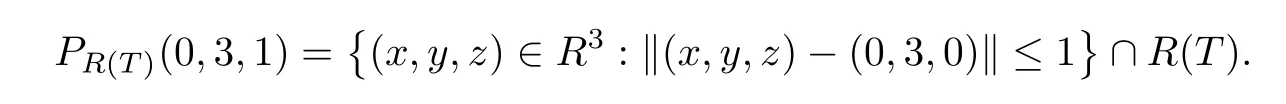
Then diamT∂(0，3，1)＞0.Moreover，it is easy to see that there exists a neighbourhoodUof point (0，3，1) such that diamT∂(x，y，z)＞0 whenevery∈U.

Definition 2.5(See[11]) A Banach spaceXis said to be uniformly convex if ‖xn-yn‖→0 wheneverand ‖xn+yn‖→2.

Corollary 2.6LetXibe a product space of uniformly convex spaces，letT:X→Ybe bounded，letN(T) be Chebyshev and let hyperplaneR(T) be 3-Chebyshev.Then there exists a homogeneous selectionTσofT∂such that continuous points ofTσandT∂are dense onY，where ‖(x1，x2)‖=‖x1‖+‖x2‖.

ProofBy Theorem 3 of[1]，we obtain thatXis an almost convex and 2-strictly convex space.Moreover，sinceX1andX2are uniformly convex，we get that every closed subspace ofXis approximatively compact.Therefore，by Theorem 2.1，we get that there exists a homogeneous selectionTσofT∂such that continuous points ofTσandT∂are dense onY.This completes the proof. □

Theorem 2.7LetXbe an almost convex and 2-strictly convex space，letT:X→Ybe a bounded linear operator，letN(T) be an approximative compact Chebyshev subspace ofXand letR(T) be a 2-Chebyshev hyperplane.Then，

(1) continuous points ofT∂are dense onandT∂is continuous onwhereG0={y∈Y:diamT∂(y)=0};

(2) there exists a homogeneous selectionTσofT∂such that continuous points ofTσare dense onandTσis continuous on

ProofBy Theorem 2.1，we know thatT∂is upper semicontinuous onY.SinceG0={y∈Y:diamT∂(y)=0}，we get that continuous points ofT∂are dense onDefine the bounded linear operatorwhere[x]∈X/N(T) andx∈X.Pick a pointy0∈Then there exists a real numberr∈(0，+∞) such thatis not a singleton for everyy∈B(y0，r).Therefore，by the proof of Theorem 5 of[1]，we get thatT∂is continuous at pointy0.This implies thatT∂are continuous onLetT∂(y)=[x(y，1)，x(y，2)]for ally∈Y.Pick a selectionTσofT∂such that

ThenTσis homogeneous.Moreover，by the proof of Theorem 5 of[1]，we obtain that continuous points ofTσare dense onandTσis continuous onThis completes the proof. □