基于热弹耦合的涡轮转子瞬态热冲击研究

徐宁，王庆超1，刘占生1，杨帆1

（1.哈尔滨工业大学能源科学与工程学院，黑龙江哈尔滨150001；2.中船重工第703研究所，黑龙江哈尔滨150078）

基于热弹耦合的涡轮转子瞬态热冲击研究

徐宁1，2，王庆超1，刘占生1，杨帆1

（1.哈尔滨工业大学能源科学与工程学院，黑龙江哈尔滨150001；2.中船重工第703研究所，黑龙江哈尔滨150078）

涡轮转子在瞬态热冲击下的热应力是最重要的参数之一，它直接影响着转子的疲劳寿命以及运行的安全性。基于热弹耦合理论推导和有限元数值仿真，针对涡轮转子的两种典型结构开展了瞬态热冲击下的热分析，研究了瞬态应力场、温度场的分布特性及其随转子结构参数的变化规律。同时，针对涡轮转子在实际工作过程中常遇到的非对称热冲击现象，进行了转子在周向非对称热冲击载荷分布下的热分析，研究结果表明涡轮转子瞬态热应力大于稳态热应力，且受到倒圆半径、轮盘厚度和盘轴比的影响，研究结果对发动机转子设计初期的热疲劳寿命评估有借鉴意义。

瞬态热冲击；涡轮转子；热应力；非对称热载荷；热疲劳寿命

当代战争要求武器装备在战备状态及应急突发事件时，能够以不惜牺牲部分发动机的热疲劳寿命来实现最短时间内的快速启动。而这种不计代价的快速启动方式，将使舰船发动机的涡轮转子无法经历暖机过程，而在最短的时间内快速达到运行工况，进入流道的气流温度与转子金属表面间存在较大的温度梯度，导致转子承受着巨大的热冲击。而由于涡轮盘常工作在复杂非均匀的热载荷环境下，极易产生热疲劳积累而导致转子总应力增加及材料性能恶化［1］。因此，对舰船发动机涡轮转子的热分析应侧重热冲击及非对称热载荷分布下的瞬态热应力变化及温度分布特性研究。

国内外学者关于发动机转子的热应力分析侧重理论计算［2-4］和在线监测［5-8］两方面。而对于转子的瞬稳态温度场、热应力计算方面的研究主要是建立理论解析模型［9-11］和有限元数值仿真［12-14］，其中理论解析模型正是通过求解热传导方程和弹性理论控制方程得到热变形及热应力，并建立普遍形式的转子热应力求解方程，这样能够较为简便地给出温度分布下的热变形及热应力，多适用于在线监测中热疲劳寿命的快速预测分析。而有限元数值仿真是基于数值法解决基本传热方程和弹性理论，它是一种能够有效准确地分析各种复杂结构和边界条件的方法。回顾近年来研究人员在进行发动机转子的热分析来看，有限元法数值仿真结果与在线实测结果也更加接近［15］。而其缺点就是计算工作量较大、需要验证仿真结果的精确性。

事实上，瞬态热冲击载荷是影响转子寿命的关键，而针对瞬态热冲击下发动机转子典型结构参数及热冲击载荷边界对热应力和温度场的影响研究却不多。同时，针对发动机转子在实际工作中受到的周向非对称热载荷的问题，如燃烧室火焰筒点火不均匀、熄火等故障，涡轮盘将承受局部热冲击载荷，极易导致转子发生热变形，最终严重影响转子热疲劳寿命并产生热致振动现象，这方面研究也较缺乏。因此，本文基于热弹耦合理论建立了转子热冲击理论计算及有限元分析模型，研究周向均布和非对称两种热冲击载荷下涡轮转子的最大热应力变化和温度场分布特性，为舰船发动机方案设计初期的热疲劳寿命预估提供有意义的借鉴。

1　转子主轴结构—热分析模型

转子主轴的瞬态热分析建模，将采用基于热传导方程和弹性理论推导出的理论方法。假设转子主轴外表面温度为Tb，初始温度分布为T0，转子外径大小为b，假设温度分布沿轴向及周向均匀分布，即温度T函数仅是半径r的函数，如图1所示。

图1　转子主轴分析模型示意图Fig.1 Illustration of the analyzed shaft model

1.1主轴结构热传导分析

上述问题可以描述为一维径向导热问题，引入过余温度函数:

圆柱坐标系下无热源的热传导控制方程为

式中:a为热扩散率，m2/s。引入过余温度函数的一维导热问题，式（2）可以简化为

采用过余温度函数表示的第一类温度边界以及条件初始条件可以表示为

运用数学物理方法中分离变量的方法，可将θ（r，τ）分解成关于时间项及空间项特征函数:

其中，时间项特征函数特解形式为

空间项特征函数解的表达式为

因此过余温度函数可以整理成:

联立式（4）、（8），可以得到关于特征值λn以及系数An的方程:

故转子主轴结构瞬态温度场函数的表达式为

式中:Jn（λnr）为贝塞尔函数，λn为贝塞尔函数特征值。

1.2主轴结构热弹耦合分析

由于转子的轴向尺寸比另外两向要大得多，故可等效为平面应变问题。根据平面应变理论有

圆柱坐标系下的运动平衡微分方程:

几何方程:

物理方程:

联立式（10）、（13），得到转子柱坐标系下瞬态热应力分量如下

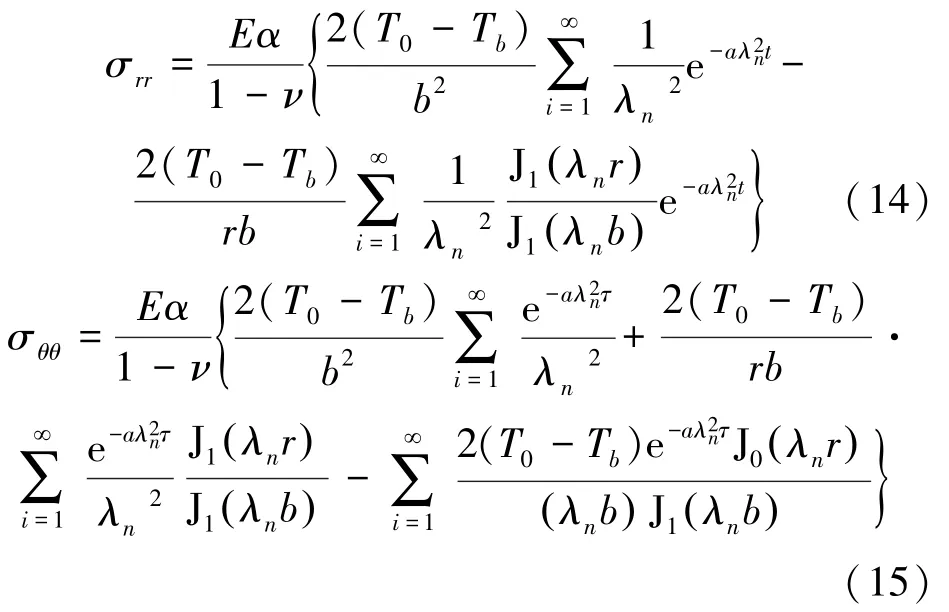
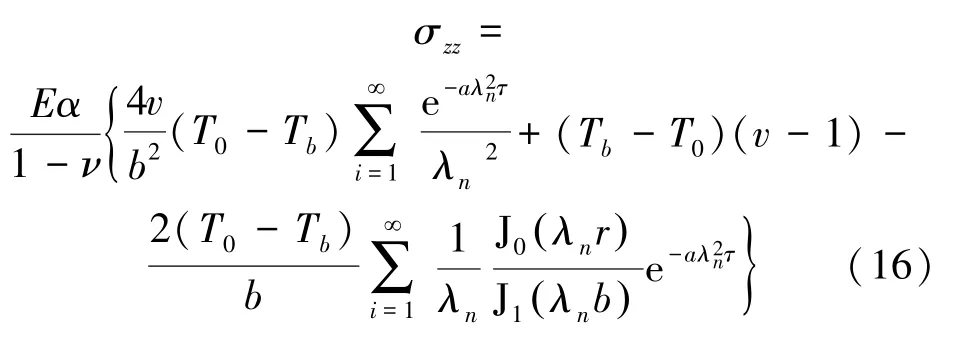
而米塞斯应力常作为衡量透平机械强度的准则，可通过下式求解:

1.3有限元仿真分析

为验证转子瞬态温度场及热应力场的理论模型，对比了有限元数值仿真结果。主轴模型共划分400个温度—位移耦合单元，并完成了网格密度及时间步长的无关性验证，二者之间的误差在5%以内，证明了本文轴单元热分析模型的准确性。

图2为瞬态热冲击载荷下圆柱体主轴的瞬态径向、周向和轴向热应力，以及瞬态温度场的变化情况，同时对比了有限元计算结果。

图2（a）所示径向热应力在初始阶段急剧增大，最大径向热应力随半径发生变化，随着半径的增加，最大径向热应力逐渐减少。在达到最大值后，径向热应力随时间的增加而减小到0。如图所示，对比在r=0，r=0.5b，r=0.75b和r=b处的径向应力两者之间的平均径向应力误差在1.03%，式（14）的理论结果与有限元结果是一致的。由于式（14）中半径在分母上，r=0理论上是径向热应力分析的奇点线，但有限元可以给出结果。在r=b处，式（14）预测的结果比有限元结果小，其他位置公式二者拟合的很好。

图2　瞬态热分析结果与有限元分析结果对比Fig.2 Comparison of the thermal analyses with finite element analyses

图2（b）给出了周向热应力分量。在中心附近位置是拉应力，而在轴外表面附近变成了压应力。式（15）预测周向热应力要大于有限元法，两者的误差不大于2.35%。半径处由于开始阶段外表面温度梯度较大，在初始阶段对外表面的网格质量要求高，而有限元模型结果受限于轴表面处的网格尺寸，而理论方法却没有这个问题。随着轴表面单元的径向尺寸减小，有限元结果更接近于理论解。

轴向热应力分布如图2（c）所示。轴向热应力的分布规律与周向相似。轴向热应力随时间逐渐接近一个定常的压应力，周向热应力逐渐变成0。对比式（16）的理论结果和有限元结果，两种方法的轴向热应力结果一致，大部分位置误差不大于0.5%。式（16）和有限元法的差别发生在初始阶段的外表面。误差在于轴表面单元的径向尺寸。

图2（d）比较了两种方法的瞬态温度分布结果。径向温度分布开始迅速变化，这是由内外径巨大的温差引起的。径向温度分布随时间变化逐渐减慢。几分钟后，温度分布恒定。式（10）的结果与有限元结果保持一致，两者之间的误差不大于1%，证实了理论模型的正确性。

图2（e）比较了式（17）和有限元法计算的米塞斯应力，由于在位置r=0和r=b处的应力分量的不同，米塞斯应力的差别在这两处比较明显。对于理论分析来说，轴线处是奇异的，理论方法无法求解。但轴表面的理论结果要比有限元法更精准，特别在瞬态传热径向温度梯度很明显的初始阶段。为了仿真瞬态热应力更准确，有限元法需要在轴表面处更优良的网格质量。

通过比较理论解与有限元仿真结果可以发现，圆柱体主轴的瞬态温度场分布及三维瞬态热应力变化规律基本一致，验证了理论解的准确性。

2　结构参数对轮盘根部倒圆结构的影响热分析

轮盘根部倒角是由主轴和轮盘构成的，是涡轮转子最普遍的一种结构形式。一般来讲，倒角处的热应力要远远大于其他位置，因此将采用有限单元模型对倒角处温度分布及热应力进行数值仿真析。

图3　轮盘根部倒圆角结构示意图Fig.3 Illustration of the disk corner structure

倒角结构如图3所示，倒圆角是由轴半径b和盘半径D形成的，倒角的半径为R，倒角结构的初始温度为T0，外表面的边界温度是Tb。理论上，由于倒圆角结构的奇异性，很难通过理论分析获得其热应力。故该处热应力将通过有限元法进行研究。材料属性与之前的研究保持一致。由于倒角处的热应力明显大于其他部位，因此该处的网格应更优良。分析前验证了网格密度和时间步长的无关性，二者差别不大于1.8%，证明了分析模型的准确性。倒角网格局部细化模型如图4所示。

图4　轮盘根部倒圆角处网格局部细化Fig.4 Local refined mesh at the disk corner

倒圆半径R=1 mm的模型，轮盘根部倒圆角处的最大瞬态热应力值随时间变化趋势如图5。可以看到在受到瞬态热冲击后，热应力在初始阶段快速增加，转子的最大瞬态热应力发生在44 s左右，峰值过后热应力逐渐减小并趋于稳定值。

倒圆半径明显的影响最大热应力，取一系列同轴径、盘径，但不同倒圆角半径（1 mm～30 mm）的模型进行研究和比较，如图6（a）所示。不同倒圆半径之间的热应力相差比较明显，最大热应力从2 338 MPa（R=1 mm）减小到 731.5 MPa（R= 30 mm）。增加倒圆半径，是减小倒角处热应力的有效方法。

将轴径与盘径之比简化成β=D/b，研究不同倒圆角R下的热应力随β的变化规律。结果如图6 （b），对相同倒圆半径下的模型，在盘轴径比β＜1.4时，热应力随β而增加。当盘轴径比β＞1.4时，热应力值逐渐降低到常值。不同模型的热应力在不同倒角时具有同样的变化趋势。

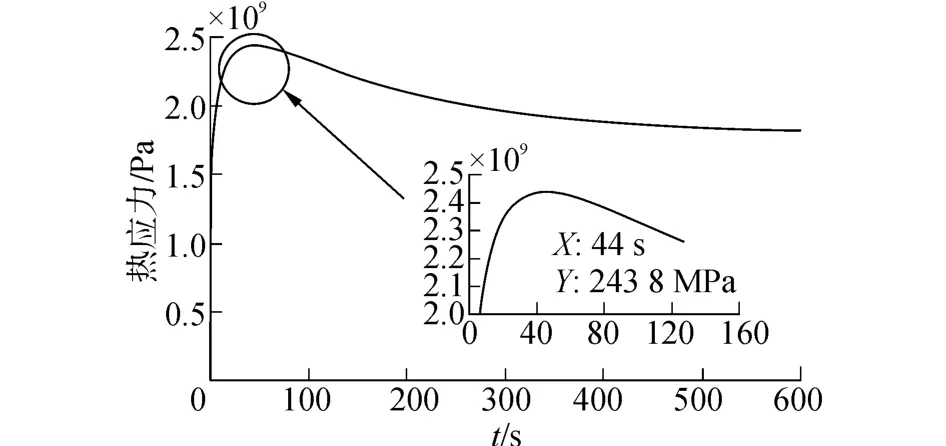
图5　轮盘根部倒角处的最大热应力随时间变化图Fig.5 Variation of maximum thermal stress at disk corner with time

当盘轴径比在 β=1.5时，倒圆半径为 R= 1 mm，3 mm，5 mm，7 mm，10 mm热应力随轴径的变化规律如图6（c）。随轴径的增加，热应力几乎不变。不同倒圆半径具有相同的结果。

图6（d）给出了不同轮盘厚度下的热应力，当轴径b=50 mm，盘轴径比β=1.5，倒圆半径R=5 mm时，研究轮盘厚度对倒角最大热应力的影响。倒角最大热应力随轮盘厚度的增加而增大。

图6（e）给出了不同盘轴径之比下最大热应力发生时间随倒圆半径的变化。可以看到发生时间随盘轴径之比增加而增加，同时增加变得的越来越慢。在同样的盘轴径之比下，发生时间随小β值增加而缓慢增加。然而在大β值下增加的更加明显。在盘轴径之比不变下，最大热应力发生时间随倒圆半径的变化。随倒圆半径的增加，发生时间急剧增加。倒圆半径越大，出现时间越久。

综上，倒圆角半径对转子最大热应力的影响较大，随倒圆角的增加最大热应力将会大幅度降低；轮盘与轴的半径比对最大热应力有一定的影响；主轴的半径对最大热应力的影响不大；轮盘厚度的增加将会增大最大热应力。

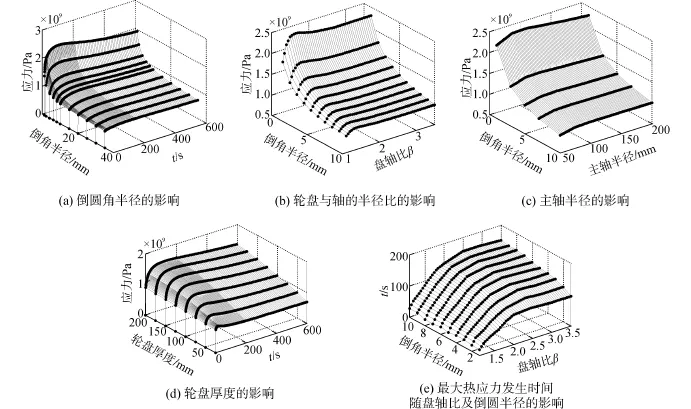
图6　结构参数对最大热应力及其发生时间的影响Fig.6 Influence of the structure parameters on the maximum thermal stress and the happening time

3　涡轮转子非对称热冲击研究

燃烧筒点火不均匀及运行时出现故障，会导致燃机涡轮盘承受瞬态非对称热载荷。这类问题属于周向非对称边界问题，即在转子某一扇区（1/6，2/6，…，5/6）加载瞬态热冲击载荷，其与周围扇区的温差骤升，在此情况下对转子进行瞬态热冲击分析。研究对象取经过适当简化后的某型燃机涡轮端转子。初始条件及边界条件用数学模型可表示为

通过对涡轮转子表面不同扇区大小进行等温差热冲击，发现转子最大热应力发生位置位于涡轮盘热冲击扇区表面与轴交界的倒角处，在一分钟内轮盘最大热应力水平随时间的变化规律如表1。

表1　各扇区角度对应的最大热应力值Table 1 The maximum thermal stress under different angles of section

如图7，轮盘热应力值在前十秒快速增长并达到极值，而后缓慢降低，其中5/6扇区的升高速率最快且热应力值也最大，而后50 s最大应力逐渐降低，热冲击扇区的角度越大，对涡轮的强度越不利。

图8表明:热冲击扇区越大，温度场、应力场分布越趋于均匀，且平均应力水平逐渐增大，对转子安全性的影响增大；同时，热应力值较大的危险区域主要集中在轮盘与轴结合的倒角的一定范围内。

4　结论

本文基于导热控制方程以及弹性力学对涡轮转子两种典型结构的瞬态热应力进行了研究，主要结论包括:

1）瞬态最大热应力水平远远高于稳态结果，倒圆半径越大，瞬态热应力降低越明显，轮盘厚度及盘轴比会影响最大热应力的大小，而主轴半径对其几乎不影响。

2）瞬态热冲击下，涡轮转子的最大热应力出现时间主要与主轴半径有关，盘轴比对其略微有影响。

3）涡轮转子瞬态在非对称热冲击下的最大热应力开始快速增大并达到极值，而后缓慢减小，非对称热冲击的扇区越大，应力极值越大。

热冲击下的瞬态热应力分析结果对涡轮转子结构设计初期评估热疲劳寿命提供有意义的参考。

［1］BUNKER R S.Gas turbine heat transfer:10 remaining hot gas path challenges［J］.Journal of turbomachinery，2006，129（2）:193-201.

［2］VULLO V，VIVIO F.Elastic stress analysis of non-linear variable thickness rotating disks subjected to thermal load and having variable density along the radius［J］.International journal of solids and structures，2008，45（20）: 5337-5355.

［3］吕智强，韩万金.采用热流法计算汽轮机转子表面热应力［J］.动力工程，2005，25（6）:765-769. LYU Zhiqiang，HAN Wanjin.Calculation of thermal stress on steam turbine rotor surfaces by the heat flux method［J］. Journal of power engineering，2005，25（6）:765-769.

［4］BHATTI S K，KUMARI S，NEELAPU M L，et al.Transient state stress analysis on an axial flow gas turbine blades and disk using finite element procedure［J］.WSEAS transactions on heat and mass transfer，2006，1（3）:329.

［5］MUKHOPADHYAY N K，DUTTA B K，KUSHWAHA H S. On-line fatigue-creep monitoring system for high-temperature components of power plants［J］.International journal of fatigue，2001，23（6）:549-560.

［6］MUKHOPADHYAY N K，DUTTA B K，KUSHWAHA H S，et al.On line fatigue life monitoring methodology for power plant components［J］.International journal of pressure vessels and piping，1994，60（3）:297-306.

［7］ANTONIO C P，LUIS S R，JESUS N G，et al.Integration of thermal stress and lifetime supervision system of steam turbine rotors［J］.Proceedings of the ASME turbo expo，2008 （2）:1035-1044.

［8］刘占生，黄世勇.汽轮机转子热应力在线监测与疲劳寿命分析［J］.汽轮机技术，2008，50（1）:9-12，28. LIU Zhansheng，HUANG Shiyong.The turbine rotor thermal-stress online monitor and fatigue life analysis［J］.Turbine technology，2008，50（1）:9-12，28.

［9］武新华，宋春汀，张新江，等.汽轮机转子热应力简化计算公式的选取［J］.汽轮机技术，2000，42（1）:20-23. WU Xinhua，SONG Chunting，ZHANG Xinjiang，et al.Selection of reduction formula in computing turbine rotor thermal stress［J］.Turbine technology，2000，42（1）:20-23.

［10］SONG G，KIM B，CHANG S.Fatigue life evaluation for turbine rotor using green＇s function［J］.Procedia engineering，2011，10:2292-2297.

［11］ZHANG Chunlin，HU Niansu，YANG Wen，et al.The research on the key factor affect the precision in stress analysis for the rotor of steam turbine［J］.Applied mechanics and materials，2013，275-277:83-86.

［12］张超，徐自力，刘石，等.采用热固双向耦合模型的转子热应力计算方法研究［J］.西安交通大学学报，2014，48（4）:68-72. ZHANG Chao，XU Zili，LIU Shi，et al.Steam turbine rotor thermal stress calculation with thermo-structural coupled model［J］.Journal of Xi'an Jiaotong university，2014，48 （4）:68-72.

［13］李朝阳，张艳春.燃机涡轮盘三维瞬态温度及应力场计算分析［J］.动力工程，2006，26（2）:211-214，294. LI Chaoyang，ZHANG Yanchun.Calculation and analysis of the transient 3-dimensional temperature and stress field of a gas turbine＇s disk［J］.Journal of power engineering，2006，26（2）:211-214，294.

［14］RAO P D，SARKAR A，SASTRI V M K.Finite element analysis of the three-dimensional transient temperature field in steam turbine casings［J］.International journal of mechanical sciences，1993，35（7）:587-595.

［15］NAGPURE H G，HANDA C C，VANALKAR A V，et al. Analysis of stresses in turbine rotor using finite element method（FEM）-a past review［J］.International journal of engineering science and technology，2012，4（3）:1037-1042.

本文引用格式：

徐宁，王庆超，刘占生，等.基于热弹耦合的涡轮转子瞬态热冲击研究［J］.哈尔滨工程大学学报，2016，37（7）:936-942.

XU Ning，WANG Qingchao，LIU Zhansheng，et al.Transient thermal impact research on turbine rotors based on thermoelastic coupling［J］.Journal of Harbin Engineering University，2016，37（7）:936-942.

Transient thermal impact research on turbine rotors based on thermoelastic coupling

XU Ning1，2，WANG Qingchao1，LIU Zhansheng1，YANG Fan1
（1.School of Energy Science and Engineering，Harbin Institute of Technology，Harbin 150001，China；2.CSIC Harbin No.703 Research Institute，Harbin 150078，China）

Thermal stress is one of the most important parameters in turbine rotors undergoing transient thermal impact，and it directly influences the safety and life of turbine rotors.Based on thermoelastic coupling derivation and finite element simulation，we analyzed the two types of typical turbine rotor structures undergoing transient thermal impact and investigated the transient thermal stress，temperature distributions，and resulting rule changes of the rotor structure parameters.In addition，to better understand the asymmetric thermal impact phenomenon of the turbine rotor when in operation，we investigated the heat conduction of the turbine rotor while undergoing circumferential asymmetric thermal impact.The results show that transient thermal stress on the turbine rotor is greater than the steady state thermal stress，and the rotor is affected by the corner radius，disk thickness，and disk to shaft ratio.These results could be used as a reference in early design stage for estimating the thermal fatigue life of a turbine rotor.

transient thermal impact；turbine rotor；thermal stress；asymmetric thermal load；thermal fatigue life

10.11990/jheu.201502026

O321；TK471

A

1006-7043（2016）07-936-07

2015-02-15.网络出版日期：2016-05-27.

国家高技术研究发展计划项目（2008AA05A302）.

徐宁（1983-），男，工程师，博士研究生；王庆超（1950-），男，教授，博士生导师；刘占生（1962-），男，教授，博士生导师.

徐宁，E-mail:xuning0451@foxmail.com.

网络出版地址：http：//www.cnki.net/kcms/detail/23.1390.u.20160527.1445.026.html