数学解题教学中对学生心理操作的四个阶段
王国宏


[摘 要]多数教师都把解题教学效果差的原因全盘推给学生的知识和能力存在问题,很少从学生的心理、情绪层面去寻找原因。利用微课题的方法,从创造激情氛围,改造问题空间,构造心理图像,锻造策略方案等入手,突破了解题教学的瓶颈,取得了较好的教学效果。
[关键词]心理操作 问题空间 心理现象
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)26-039
德国教学设计专家彼得森认为:“影响解题教学的前提很多,其中哪些最重要呢?认知心理学条件和社会文化若能在解题教学设计中被予以重点关注,就会形成独特的解题风格和奇特的解题教学效果。”
近些年的解题教学研究给出解答问题时应遵从的法则:始态(initialstate)——教学习题中的已知条件;终态(Goalstate)——解题时要达到的最终目标,教学题中要求的;操作法则(operafpr)——应用心理,情绪及法则,变动态为终态。
数学解题属于问题解决的范畴,是认知心理学的一个重要课题。笔者在解题教学中,主要从以下几个阶段来进行心理操作。
第一阶段:自控逻辑起点,创造激情氛围
“情绪脑”在解题过程中的重要性及其功效是无可否认的,但在解题教学中教师还是对经常出错的学生缺乏耐心辅导,缺少心理诱导,缺失技能指导,总是大声呵斥这部分学生,较少顾及学生的逻辑起点和情绪心理。为改变现状,在设计教案时,笔者着重了解学生的情绪状态及认知心理,依据各层次的需求设计题目,注意在解题前与学生在情感上拉近距离。
如教学两位数乘法时(篮球场的面积计算),先让学生自选方法,再予以介绍。
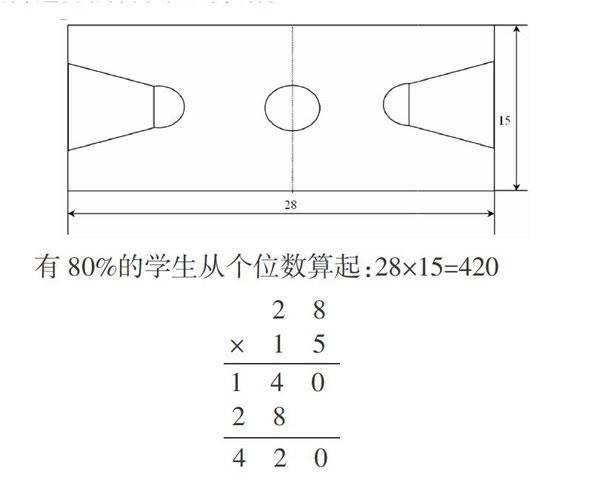
有80%的学生从个位数算起:28×15=420
有10%的学生列式:15×14×2=420
有5%的学生从高位算起:
还有5%的学生列式“30×15-2×15”。
特对于后两个5%的学生,笔者认为他们解题基本功扎实,有自己的思想,随即在课堂上予以“点赞”。事实证明,分层教学对各层面的学生来说很重要。
第二阶段:调控搜索“模块”,改造问题空间
一旦接触到题目开始解题时,学生原有的知识经验和实践感知就会向着一定的方向前进,搜索识别后而提取贮存于大脑长期记忆里相近与相似的“数学模块”,问题就有可能被直接解决。对于一个比较复杂的数学问题,不能强求只调动一次“数学模块”,因为很多时候是要通过多次信息加工后才能解决的。
如,在“植树中的数学问题”教学中,教师出示题目(故意缺少一个条件):在学校一段长15米的小路的一边种树,一共要种多少棵?
学生都意识到这个题无法解答,于是,教师让学生补充条件。
生1:我补“每隔3米种一棵”这个条件。
生2:我想生1的条件不完整,应该再加上一个“两头都种”。
生3:我不同意生2的“两头都种这个条件”,因为这条路的两头都有房子(墙挡着),两头都不能种树。
生4:我先画了个图:
师:我赞同生4的建议,你们可以根据自己的不同理解,先建立一个“模块”,然后根据具体情况作出“充分的补充条件”。
生5:画图后我就明白了。补充“每隔3米种一棵,如果两端都种,如果只种一端,如果两端都不种(这样三个如果)”,那么题目就完整了。
师:请大家看图数一下,有几个间隔?有几棵树?
生6:我可以用手指和间隔”来说明吗?
师:当然可以,请你展示一下。
师:“间隔数”与“植树棵数”有什么数量间的关系?
生6:间隔数总比树的数量少1,树的数量比间隔数多1。
(师出示“小路长45米,每隔9米种一棵”,“小路长90米,每隔18米种一棵……”,学生都惊呼“怎么都是同一个答案”。)
师:如果小路总长100米,每隔2米种一棵,并且两旁两端都要求种,这时也是间隔数比树的数量少1吗?
生(由疑惑的神情转为坚定的回答):两端都种,则“间隔数”比“棵数”少1……
渗透数学思想方法是数学广角的目标之一。五年级学生正处于具体形象思维向抽象逻辑思维转折的时期,所以搭建画图这一数形结合的平台,一方面帮助学生建立植树问题的表象,另一方面帮助学生将文字信息和思维耦合在一起。同时追问:“如果总长100米,间隔距离2米,间隔数有几个?那植树棵数呢?如果间隔数是80个,那植树几棵?如果间隔数是n个,那植树几棵?”促使学生从形象思维向抽象思维过渡,从而领会教材背后渗透的一一对应思想。
第三阶段:掌握操作环节,构造心理图像
这一阶段是十分重要的阶段,包括归纳、排除、分解、组合、迁移、选择、衔接、沟通等多种操作环节。事实上,在解题的操作过程中,学生的个性、风格、思路都不完全相同。因此,教师在解题教学中不应该只用“唯一”的思路,应当集思广益,让每位学生都能找到最适合自己的方法。
如教学五年级“方程”的问题时,先出示:远望高塔有七层,红灯盏盏倍加增,共计三百八十一,请求顶层灯几盏。
以诗歌形式出现的题目,学生倍感新鲜和意外:在情感上有亲切感,在心理上容易接受。
师:关键词是“97层,倍加增,381”。(让学生构造对题目的心理图像)
生1:我想用倍数问题的方法来解决。
生2:我想用倒推方法来解决。
生3:我想用画图的方法。
生4:我想设未知数,用方程来解决。
……
师:大家的心理图像都构造得很好。无论是用倍数、倒推、画图,还是其他方法,都可以归纳为一句俗语——万变不离其宗,即用方程来解答(因为方程解法是万能的)。设顶层为x盏,
x+2x+4x+8x+16x+32x+64x=381
x=3
由这一例示可以看出,学生提取的每一个知识模块所包含的知识各不相同,每一模块有其各自的特点和应该满足的规律。这些规律就是学生的心理操作模块和操作规程。把这些模块自然地衔接起来,就构成了清晰的心理图像,问题就迎刃而解。
第四阶段:监控反馈矫正,锻造不同策略
经过第三个阶段,解题的策略已基本形成,再通过编辑、优化、计算、检验,就更为条理化,这就达到了问题的终态。这是把加工完毕的信息分为两部分:其一,通过职能器官输出;其二,又回输(反馈)到大脑成为新的“模块”,储存在长期记忆里。
关于策略的培养有一个度的问题。以“鸡兔同笼”为例:鸡兔共8只,有22只脚,鸡兔各有多少只?
解决此问题的策略比较多样。
策略1:尝试与猜想。1只鸡,7只兔,腿的总条数是30只,腿多了,减少兔子的数量,再尝试。
策略2:列表尝试。鸡兔各4只,那么腿24只,腿少了,增加鸡的数量,再尝试。
策略3:画图法。先按照都是鸡画好,再在此基础上添上腿,添上2只腿就表明多了1只兔。
策略4:假设全是鸡,也可以假设全是兔,也可以假设一半是鸡一半是兔。
策略5:方程法。用□表示鸡的只数,用○表示兔的只数,根据已知条件可以发现□+○=8,2□+4○=22;由此可以得到2(□+○)+2○=22,2○=22-16,○=3。
策略6:面积图法。利用长方形面积公式来计算组合图形的面积。
可以发现,同一问题,有不同的解题策略,教师教学时要针对具体内容预设教学目标。
波利亚的《怎样解题》在全球范围内有很大的影响,在具体设计与实施解题教学方案时,笔者在牢牢把握“弄清问题→拟定计划→实现计划→回顾反思”的基础上,采用了自控情绪心理,调控搜索模块,掌控操作环节,监控反馈矫正,即波利亚的四个解题步骤的具体落实。采用“独特的风格,奇特的效果”措施以来,学生解题时理解题目透彻了,分析条件仔细了,列式解答正确率提升了,也形成了善于反思的习惯。
总之,如一位心理学家所说:“世界上找不到两张相同的面孔,这也可以说明,世界上也找不到相同的两个人的心理状态。”每个学生都有不可复制的学习心理特点和学习差异,教师若能遵循心理规律,尊重学生的心理情绪,那么解题教学效果将会得到巨大的提升。
(责编 童 夏)

