平稳中凸显变化 变化中体现创新
——2016年浙江省高考数学理科解析几何题评析
张艳宗 卢 明
(浙江省海盐县元济高级中学,314300)
○高考之窗○
平稳中凸显变化 变化中体现创新
——2016年浙江省高考数学理科解析几何题评析
张艳宗卢明
(浙江省海盐县元济高级中学,314300)
2016年,是浙江省“老高考”模式的收官之年,试卷的命题走向、难易程度等颇受广大教研员和一线教师的关注.今年的数学试题,不乏许多立意高、角度宽、视点多等积极的评价,且注重考查学生数学思想方法和数学素养.对于理科数学第19题,全省平均为7.01分,虽然平均分略高于往年,但广大教师对其评价褒贬不一.
一道试题,为什么会引起这么大的争议呢?本文试图分析此题的特点,探讨试题的解题思路及方法,挖掘试题背景,研究试题带给我们的启迪和反思.
一、试题呈现
(1)求直线y=kx+1被椭圆截得到的弦长(用a,k表示);
(2)若任意以点A(0,1)为圆心的圆与椭圆至多有三个公共点,求椭圆的离心率的取值范围.

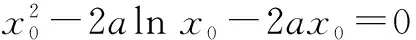

联立可得2lnx0+x0-1=0.

又m(1)=0,x0=1,即

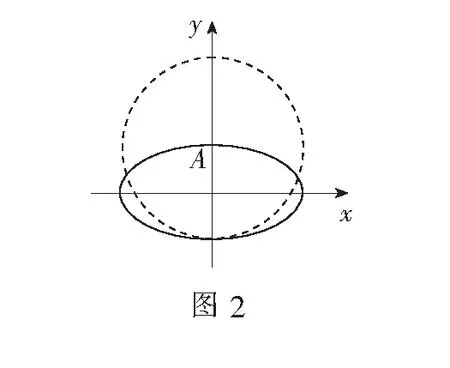
(3)不妨令1≤x1 因为0 由(1)得f(x1) ∵|f(x1)-f(x2)|>|g(x1)-g(x2)|, ∴f(x2)-f(x1)>g(x2)-g(x1), ∴f(x2)-g(x2)>f(x1)-g(x2). ∴h(x)=f(x)-g(x)=x2-2alnx-2ax在[1,2]上递增, 本题表述简洁明了,一题两问,由浅入深,起点低、落点高.第(1)问考查直线与椭圆的位置关系,弦长公式等基础知识;第(2)问一改以往求三角形面积的套路,变成研究圆与椭圆的位置关系,体现了命题人稳中求变、推陈出新的用心.这种新变化出乎广大师生意料,对圆与椭圆的性质等知识提出了较高要求,对考生的直觉判断、探究思辨、转化化归、代数运算等方面提出新的挑战.另外,此题还突出考查解析几何的基本思想方法、转化与化归思想、数形结合思想、函数与方程思想. 本题第(1)问设问常规,思路清晰,考生容易上手;第(2)问几何背景丰富,解法灵活,大部分考生在短时间内难以解决. 解(1) 直线y=kx+1过定点A(0,1),设此直线被椭圆所截的线段为AP,联立 得(1+a2k2)x2+2a2kx=0, (2)分析点A(0,1)是椭圆的上顶点,以A(0,1)为圆心的圆与椭圆的交点个数可能是2个、3个、4个或0个.于是,要求满足“圆与椭圆至多有3个公共点”的参数a的取值范围,可以通过求满足“圆与椭圆有4个公共点”的参数a的取值范围的“补集”来解决. 解法1假设圆与椭圆的公共点有4个. 以点A(0,1)为圆心,半径为r(r>0)的圆的方程为x2+(y-1)2=r2.联立 得(a2-1)y2+2y+r2-a2-1=0. 令f(y)=(a2-1)y2+2y+r2-a2-1,存在正实数r,使得f(y)=0在y∈[-1,0]时有2个实数根,从而 评注关于曲线的交点问题,一般的处理方法是联立曲线方程,通过对方程根的个数的研究来讨论曲线的交点个数,即用代数的方法来研究几何问题,这也是解析几何最本质的思想.与之对应的数学思想有等价转换、数形结合、函数与方程.本题的难点在于直接求满足“圆与椭圆至多有三个公共点”的参数a的取值范围比较困难,需要将问题转化,用求“补集”的思想来确定a的取值范围.本题的亮点:离心率的范围是通过求函数的值域来获得的,平时比较少见.本题的争议点是以往对“求两个二次曲线的交点问题”要求不太高,近年来的高考试题中也从未出现过,因此一些老师认为此题涉嫌“超纲”. 真的是“超纲”吗?为了慎重起见,笔者查考了2014版《浙江省普通高中数学学科教学指导意见》,“发展要求:掌握利用曲线的方程研究曲线几何性质的基本方法.” 由此可见并没有限制不能出现“两个二次曲线”背景,故认为本题“超纲”有点牵强. 下面介绍命题组提供的解法. 解法2假设圆与椭圆的公共点有4个,由对称性可设y轴左侧的椭圆上有两个不同的点P,Q满足|AP|=|AQ|.记直线AP,AQ的斜率分别为k1,k2,且k1,k2>0,k1≠k2. 由k1,k2>0,k1≠k2,得 评注上述解法主要应用了圆与椭圆的几何性质、直线与椭圆的位置关系、弦长公式等基础知识,通过代数变形,利用“非负性”构造出关于a的不等式求解,所涉及到的知识、方法并不超纲.高考结束后,笔者了解相关情况,很少有学生采用了此法,且此法的计算量以及代数变形技巧较强,较难想到. 除以上两种解法外,还有没有相对简单、学生易于理解的解法呢? 解法3若a=a0(a0是某个正常数),以点A(0,1)为圆心的圆,半径r从0开始增大,圆与椭圆开始时有2个公共点.当圆与椭圆恰有3个公共点时,如图2.r继续增大,圆与椭圆可有4个、2个、0个公共点,不符合题意.若a>a0,变化情况相同. 若a 设P(x0,y0)是椭圆上任意一点,则 评注先对圆与椭圆的交点个数进行分析,讨论两者的位置关系,再利用代数方法求解,计算量大大减少.在以上分析中发现,任意以点A(0,1)为圆心的圆与椭圆相交,存在有0个、2个公共点的情形,因此原题中“至多有三个公共点”可改为“至多有两个公共点”.命题人之所以采用“至多有三个公共点”设问,或在于降低问题的难度,也便于“补集思想”的应用. 在第(2)问圆与椭圆公共点个数的研究过程中,我们发现这样一个几何问题:即比较椭圆与圆的弯曲程度.事实上,这就是此题的高等数学背景——曲率及曲率圆. 定义2在曲线AB点M处的法线上,在凹的一侧取一点为圆心,过点M作一个圆,使得这个圆的曲率与曲线AB在此点处的曲率相等,这个圆叫做曲线在点M处的曲率圆,又叫密切圆.密切圆的圆心叫做曲线在点M处的曲率中心,密切圆的半径叫做曲线在点M处的曲率半径. 在点M处的曲率圆与曲线存在如下关系:一是有公切线;二是凹向一致;三是曲率相同.高等数学中有如下结论: 结论曲率计算公式 由此我们不难得到 由解法3知,以点A(0,1)为圆心的圆与椭圆至多有3个公共点,即圆与椭圆有0个、2个公共点两种情形,只要比较椭圆在下顶点B(0,-1)处的曲率与以点A(0,1)为圆心, 1.把握本质,注重转化 解析几何是用代数的方法来研究几何问题的一门学科,但其本质上还是一个几何问题,只不过是调换了一种研究方法而已.因此,在求解过程中,要注意合理运用几何方法,若能根据图象特征,运用平面几何知识,如中位线、射影定理、圆的有关性质、定理等,可以简化繁琐的代数运算,达到事半功倍的效果.同时,还要注意2个转化:一是将语言转化为式子,实现已知条件的具体化;二是将图形转化为式子,如图象的交点问题,可以通过数形结合、等价转换,将交点问题转化为方程的根的问题,体现解析思想. 2.加强运算,提升能力 运算能力是突破解析几何学习的一道“槛”.解析几何的学习不仅需要较强的思维能力,也需要较强的数据、字母的运算能力.在教学过程中,要重视计算能力的培养与训练,克服学生中克服“怕繁、怕难”的情绪,或“只重思路、轻视计算”的浮夸学风,努力纠正“眼高手低”的毛病,课堂上教师要多示范,鼓励、督促学生详写演算过程,重视数学计算所需的数学能力和心理品质的养成,切实提高学生的计算能力. 3. 一题多解,优化思维 解析几何题往往入口比较宽,是训练学生发散思维、培养创造灵感的好机会.教师在教学过程中应当重视一题多解与一题多变,引导学生在做中领悟,在做中反思,帮助学生养成“做一题,想一想”的良好习惯,发展批判性思维、逆向思维,提升思维品质,促进学生在遇到新的问题情境时能自觉运用所学知识合理地展开联想、实现迁移.


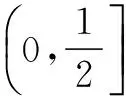
二、解法探讨
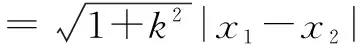


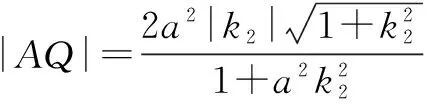




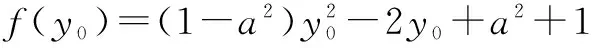
三、背景探源

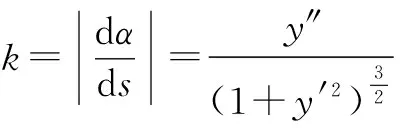


四、教学建议

