双换元法求二元变量的最值问题
2016-10-09 06:36:29李东进
高中数学教与学 2016年17期
李东进
(江苏省苏州市苏州新草桥中学 215011)
○短文集锦○
双换元法求二元变量的最值问题
李东进
(江苏省苏州市苏州新草桥中学 215011)
最值问题,特别是二元变量的最值问题是教学的难点,同时也是各级各类调研考试、高考的热点.纵观一些高考、模拟试题,这类最值问题由于结构复杂,难以将问题转化为一元问题,导致处理难度大.笔者发现对这类最值问题采取双换元的方法,可以收到意想不到的效果.本文结合教学实践略作探讨,供大家参考.
一、分式求和型的最值

简解设2a+b=x,b+1=y,
则x>0,y>1,



此类问题的求解方法很多,考虑到和式的分母较为复杂,分子简单,所以可以对分母进行双换元再化简,变为关于新变量的简单式子,再利用基本不等式求解,这样的化归大大减少了思维量.

二、旋转双曲线条件下的最值

简解2x2+xy-y2=1,即
(2x-y)(x+y)=1.
设2x-y=m,x+y=n,则mn=1,
且x-2y=(2x-y)-(x+y)=m-n,
5x2-2xy+2y2=(2x-y)2+(x+y)2
=m2+n2.

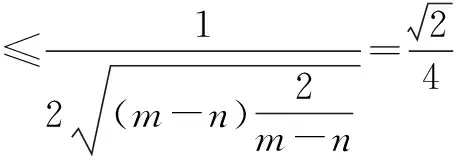

本例中的方程2x2+xy-y2=1对应的曲线,其实是旋转后的双曲线.对于此类最值的求解可以将条件进行因式分解再对两个因式双换元,将所求表达式利用待定系数法表示为换元后的双元表达式,结合基本不等式知
猜你喜欢
北京支部生活(2023年7期)2023-07-24 09:18:57
中学生数理化·七年级数学人教版(2021年12期)2021-12-31 05:16:38
小天使·一年级语数英综合(2021年12期)2021-03-21 23:40:19
考试与评价·高二版(2020年3期)2020-09-10 13:04:38
西部论丛(2019年25期)2019-10-21 05:42:40
美文(2018年24期)2018-12-18 09:41:07
中学教学参考·理科版(2017年8期)2018-02-24 21:32:13
中学生数理化·高三版(2017年2期)2017-04-21 10:50:59
福建中学数学(2017年1期)2017-04-21 10:35:29
中老年健康(2014年9期)2014-05-30 22:16:47

