高三数学综合测试



高三数学综合测试

一、填空题(本大题共14小题，每小题5分，共70分)

1.已知集合A={1,a}，B={1，3，4},且A∩B={1,3}，则实数a的值为______.

3.对一批产品的长度(单位:毫米)进行抽样检测,样本容量为200,下图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为______.

4.某学校高三有A,B两个自习教室,甲、乙、丙三名同学随机选择其中一个教室自习,则他们在同一自习教室上自习的概率为______.

5.执行如图所示的流程图,会输出一列数,则这列数中的第3个数是______.

所以tanAtanBtanC最小值是8(此时∆ABC为等边三角形).

评注该题解题方法朴实,由已知推出B=C,转化得到关于tanC的函数,再利用导数求解最值.与原题目相比,变式题对数学思维水平要求较低,可由已知条件直接推导出B=C,思维障碍较少；而原题目则需要从解题目标出发分析变形的方向,思维挑战较高.

综上所述,2016年江苏卷第14题确实是一道值得点赞的小题.试题源于教材,贴近江苏学生的实际情况.作为一道填空题,试题有机结合了三角、不等式、函数等知识点,渗透了消元、化归等思想方法.该题有多种解题方法,既有“通性通法”,同时又不排斥“特技”,这对今后的命题、教学和应试都起到了很好的导向作用.

那么不禁要问,为什么很多学生在考场上会手足无措,遭遇“思维困境”?笔者认为这主要还是由于教师在教学中惯于“题型”训练,忽视能力培养,导致学生数学思维水平不高,分析问题能力不足.因此要想学生能在高考中立于不败之地,乃至终身受益,在教学中就务必坚持思维为重,聚焦能力培养,回归数学教育的本源.

7.已知等差数列{an}的前n项和为Sn,且2S3-3S2=12,则数列{an}的公差是______.

8.已知一个圆锥的底面积为2π,侧面积为4π，则该圆锥的体积为______.

12.已知圆C:x2+y2-2x-2y+1=0,直线l:3x+4y-17=0.若在直线l上任取一点M作圆C的切线MA,MB,切点分别为A,B,则AB的长度取最小值时，直线AB的方程为______.

13.已知函数

g(x)=kx+1，若方程f(x)-g(x)=0有两个不同的实根,则实数k的取值范围是______.

14.已知不等式(ax+3)(x2-b)≤0对任意x∈(0,+∞)恒成立,其中a,b是整数,则a+b的取值的集合为______.

二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)

(1)求f(x)的解析式；

16.(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°，点E是PC的中点,且平面PBC⊥平面ABCD.证明：

(1)AP∥平面BED；

(2)平面APC⊥平面BED.

(1)求水上旅游线AB的长;

(1)求椭圆M的方程;

(2)如图,椭圆M的上、下顶点分别为A,B,过点P的直线l与椭圆M相交于两个不同的点C,D.

② 当AD与BC相交于点Q时,试问:点Q的纵坐标是否是定值?若是,求出该定值;若不是,说明理由.

19.(本小题满分16分)已知{an}是等差数列,{bn}是等比数列,其中n∈N*.

(1)若a1=b1=2,a3-b3=9,a5=b5,试分别求数列{an}和{bn}的通项公式;

(2)设A={k|ak=bk,k∈N*}，当数列{bn}的公比q<-1时，求集合A的元素个数的最大值.

(1)若曲线y=f(x)在x=1的切线方程为y=e(x-1)，求实数a,b的值；

(2)① 若a=-2时，函数y=f(x)既有极大值,又有极小值,求实数b的取值范围;

② 若a=2,b≥-2，且f(x)≥k(x)对一切正实数x恒成立,求实数k的最大值(用b表示).

参考答案

一、填空题

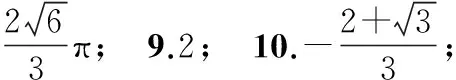
二、解答题

(2)由(1)知f(x)=2cosx.

所以f(α-β)=2cos(α-β)

=2(cosαcosβ+sinαsinβ)

16.(1)设AC∩BD=O，ABCD是平行四边形,故O为BD中点.连结OE，因为点E是PC的中点，所以AP∥OE，OE⊂平面BED,AP⊄平面BED，所以AP∥平面BED.

(2)因为平面PBC⊥平面ABCD，∠PCB=90°，故PC⊥平面ABCD.又BD⊂平面ABCD，所以PC⊥BD.而底面ABCD是菱形，故AC⊥BD，又AC∩PC=C,所以BD⊥平面APC.BD⊂平面BED，所以平面APC⊥平面BED.

17.(1)以点O为坐标原点，直线OM为x轴，建立直角坐标系如图所示.则由题设得A(6，0)，直线ON的方程为y=-3x,Q(x0,3)(x0>0).

及x0>0得x0=3,∴Q(3,3)，

∴直线AQ的方程为y=-(x-6),

即x+y-6=0.

(2)设试验产生的强水波圆P，由题意可得P(3，9)，生成t小时时，游轮在线段AB上的点C处，则

∴C(6-18t,18t).

PC2=(18t-3)2+(18t-9)2

>r2=9at,

(1+4k2)x2+16kx+12=0.

由Δ>0,可得4k2>3,且

=(1+k2)x1x2+2k(x1+x2)+4

联立方程组，消去x得

19.(1)设数列{an}的公差为d(d≠0)，数列{bn}的公差为q(q≠0,1)，则

(2)不妨设an=a+bn(b≠0),bn=nq2(pq≠0,q≠1),则

qn-tn-s=0

(*)

最多有多少个解.

综上，当n∈N*时，方程(*)最多有3个解.

②当t<0时，同理可知方程(*)最多有3个解.事实上，设an=6n-8,bn=(-2)n时，有a1=b1,a2=b2,a5=b4,所以A的元素个数最大值为3.

20.(1)由题意知曲线y=f(x)过点(1，0)，且f′(1)=e.又因为

解得a=3,b=-2.

(2)①当a=-2时，函数y=f(x)的导函数

所以，当且仅当b>1+ln 2时，b=g(x)有两个不同的解，设为x1,x2(x1

x(0,x1)x1(x1,x2)x2(x2,+∞)f'(x)-0+0-f(x)↘极大值↗极小值↘

此时，函数y=f(x)既有极大值，又有极小值.

即实数k的最大值为(2+b)e.