中国铜期货市场期货价格期限结构研究

部慧(北京航空航天大学经济管理学院,北京100191)

中国铜期货市场期货价格期限结构研究

部慧
(北京航空航天大学经济管理学院,北京100191)

分析了我国上海期货交易所的铜期货不同到期期限的期货合约的价格数据,研究了铜期货价格的期限结构,样本期为2004-09—2012-12.结合Kolb提出的统计量,首先对铜期货市场的现货升水特征进行了统计分析.接下来,结合Gibson等提出的似无关回归分析(SUR)的方法,利用代理变量对现货价格和便利收益率的时间序列性质进行了检验,揭示了现货价格和便利收益率均是均值回转的过程,也说明Schwartz提出的两因子模型适用于拟合我国的铜期货合约价格.因此,本文构建了价格期限结构的两因子模型,并利用状态空间模型和卡尔曼滤波方法进行估计.实证结果揭示了我国铜期货在金融危机之前具有相对稳定的现货升水特征,尤其在2006年之前更为明显;金融危机时期该特征曾发生异常逆转;危机过后较长一段时间铜期货市场无明显特征,近期现货升水特征逐渐恢复但仍很微弱.

期货市场;现货升水假说;库存理论;期限结构模型

1　引　言

商品期货定价是期货研究中的一个关键问题.商品定价中的一个问题是期货价格是否是未来预期现货价格的无偏估计,这源于凯恩斯的现货升水假说［1，2］.期货市场是否存在现货升(贴水)特征以及这种特征该如何解释是研究者们关注的问题.早期的研究主要在于探讨期货市场价格的期限结构特征,后期的研究主要在于探讨某种特征的存在是否源于风险溢价的转移或者其他原因.与此问题相关的商品期货定价理论主要包括库存理论和风险溢价理论.库存理论得到了相对一致的认可,可用于解释商品期货价格的期限结构的特征.基于库存理论,从20世纪80年代至20世纪90年代研究中开始对商品现货价格和便利收益建立随机过程模型,20世纪90年代后期的研究更是关注整个商品期货期限结构的随机过程建模.期货价格期限结构模型从单因子模型不断扩展到三因子模型,已经可以模拟出较为相近的期货价格曲线［3］.

由于商品期货价格的期限结构关系到套期保值和套利策略的制定和执行效果,因此研究商品期货价格的期限结构问题对市场分析师和研究人员都具有重要价值.近几年,越来越多的研究将商品期货期限结构的研究结果用于讨论期货的投资策略,如迁仓收益、战术性配置［4，5］以及期货价格预测［6］等.对我国期货市场商品价格期限结构问题的研究尽管已有一些工作,例如文献[7–9]曾讨论过单因素模型或者对季节性因素做过讨论,但对问题的深入讨论仍是需要的.

2　文献综述

2.1现货升水假说的实证研究

Keynes［1］和Hicks［2］提出的现货升水假说认为,套期保值者通过期货合约把价格变化的风险转移给愿意承担风险的投机者从而降低自身的风险,因此套期保值者愿意持有一个预期收益为负的期货合约,而投机者由于承担了风险会要求相应的风险补偿.如果市场上以空头套期保值者占主导,那么在到期日前期货价格会低于未来的预期现货价格即现货升水(normal backwardation).如果市场上以多头套期保值者占主导,则在到期日前期货价格会高于未来的预期现货价格即现货贴水(contango).对于现货升水假说的实证检验,最早的研究是基于检验期货价格在到期日之前上涨这一推论进行的.Telser［10］检验了期货合约的价格趋势,结论并不能支持现货升水假设.Cootner［11］通过检验期货合约的价格趋势以及投机者收益,却得出了与Telser相反的结论.Kolb［12］利用多种检验期货价格趋势的方法对更多的期货品种在更长的样本时间段里进行了检验,认为仅有一些金属和豆类的期货表现出了现货升水特征,大多数期货品种并没有现货升水特征.Lee等［13］对美国期货市场上29种商品期货价格趋势进行了检验,认为现货升水现象存在.

检验期货价格在到期日之前是否上涨的研究仅能说明是否存在现货升水现象,但并不能说明是否存在风险溢价的转移.因此,之后的研究者着重探求期货市场是否存在市场风险溢价.Cootner［11］提出了风险溢价模型,认为商品期货价格等于预期现货价格以风险溢价率折扣后的价格.Dusak［14］在资本资产定价模型(CAPM)框架下检验了市场风险溢价,他发现期货合约的系统风险并不显著异于零,由此认为并不存在风险溢价的转移.Carter等［15］在文献[14]的基础上加入了投机者头寸的虚拟变量,并且在市场组合中加入了商品指数,发现了与文献[14]相反的结论,支持现货升水的假说.Marcus［16］和Baxter等［17］的研究发现,当在CAPM模型中采用另一个市场指数后,原来存在的风险溢价就并不存在了.研究者们还将研究扩展到基于套利定价理论(APT).Ehrhardt等［18］在APT框架下对风险溢价进行了研究,结论认为期货市场并不存在风险溢价.M iffre［19］构造了因子敏感系数变化的APT模型,发现美国期货市场上的玉米、大豆及小麦等品种上的套保者会给投机者提供了一个正的风险溢价,而外汇期货市场上风险溢价却是负的.

关于投机者获得的超额收益是来源于风险转移还是投机者的价格预测能力也成为争论的焦点之一.Houthakker［20］和Rockwell［21］区分了投机者从预测价格的能力中获得的收益.他们将投资者分成3类:大套期保值者、大投机者和小额交易者.Rockwell认为只有在投机者没有预测价格能力却能获得超额收益时才能说明期货市场存在风险溢价转移.他假设没有价格预测能力的小投机者遵循天真投资策略:套保者为多头(空头)时,他们为空头(多头).Rockwell的实证结果说明天真投资者的收益是零,期货市场并不存在风险溢价的转移;但是大投机者却能够获得正的超额收益,这应归结为大投机者预测价格的能力.Houthakker［20］和Rockwell［21］研究的缺陷在于并没有使用统计显著性检验.基于此,Chang［22］在Rockwell对投资者的分类和对天真投机者定义的基础上,通过统计显著性检验证明期货市场有现货升水的特征.

2.2库存理论和期货价格动态模型

传统库存理论将期货价格的期限结构与商品合约的库存水平联系起来.根据库存持有成本模型,在无套利均衡条件下,期货价格满足

其中r为年化无风险利率,u为库存成本,y为便利收益率.或者表示为

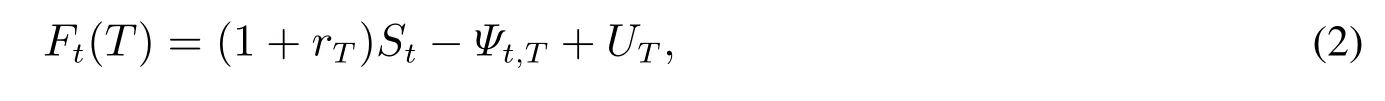
其中Ft（T）是在时刻t距离到期日还有T期的期货合约价格,Ψt，T代表从t时刻到t+T时刻的边际便利收益,rT为T期的无风险利率,UT是T期的库存成本.Ψt，T-UT或y-u被称之为净便利收益或净便利收益率.便利收益的概念由Kaldor［23］首次引入,用以衡量持有现货库存由于可以用于消费从而产生的价值,这是期货合约的持有者所没有的.如果r＜y-u,那么Ft（T）＜St,即持有现货库存所带来的便利收益越高,期货合约越呈现现货升水现象.

最早将库存和期货价格期限结构关系用实证结果呈现出来的是Working［24］,但该工作随后引来诸多讨论和批评.Carter等［25］再次检验了Working曲线,并认为该曲线是合理的.Gorton等［26］研究了美国期货市场31种期货在1969—2006期间的期货价格和库存数据,揭示了便利收益率与库存是递减非线性的关系,并且提出期货合约价差是揭示商品期货风险溢价的良好指标.Deaton等［27］基于一般均衡分析提出了一个商品定价和库存的模型,该模型将库存水平与未来现货价格的方差联系了起来.Pindyck［28］用一般均衡的思想分析了商品的现货市场和库存市场,讨论了商品价格、生产和库存的短期动态关系,解释了三者之间是如何相互联系的;并讨论了期货价格、现货价格与库存之间的关系.Lin等［29］的研究发现,当现货价格低时存货水平和便利收益的相关性较小;当现货价格高时,存货水平和便利收益的相关性较大;同时利率的变化会影响到原细的便利收益率.

从20世纪80年代至20世纪90年代开始,研究中对商品现货价格和便利收益率建立了随机过程模型;20世纪90年代后期的研究则关注整个商品期货期限结构的随机过程建模.期货价格期限结构模型从单因子模型不断扩展到三因子模型,已经可以模拟出较好的期货价格曲线［3］.单因子模型以现货价格为因子,假设便利收益和利率为常数.对现货价格的动态过程有两种设定方式:一种是假设现货价格服从几何布朗运动,例如文献[30–32]等;另一种是假设现货价格服从均值回转过程,例如文献[33–37]等.我国的研究大多采用单因子模型,例如文献[7–9]曾讨论过单因素模型或者对季节性因素做过讨论.

为了使模型更符合现实,研究工作开始引入两因子或三因子模型.两因子模型中第二个因子的选择大多为便利收益率,例如Gibson等［31］,Schwartz［36］,Lautier等［38］.还有一些研究中第二个因子为长期价格,例如Schwartz等［39］.三因子模型中更多的考虑利率因素,例如Schwartz［36］.近期的一些研究不断修正三因子模型.Cortazar等［40］提出了只和商品价格相关的三因子模型;Casassus等［41］将便利收益率视为现货价格和利率的函数来构建三因子模型,并且允许风险溢价是时变的.Liu等［42］指出工业产品的便利收益率往往有异方差性（便利收益率的变动随着便利收益率的增加而增大）,因此在建立三因素模型时需要考虑异方差性.

3　研究方法

本文对我国的铜期货合约价格建立由Schwartz［36］提出的两因子模型,从而构建期货期限结构曲线.虽然是沿用两因子模型,但本文试图对我国期货价格进行更加详细的统计检验,以使得对模型的设定和参数选择更加合理有效.本文将检验我国铜期货市场数据的微观特征,检验现货价格和便利收益率是否为均值回转的过程.检验的方法将采用Gibson等［31］的方法,并做了适当修订.由于便利收益是不可观测变量,而现货价格方面,虽然有铜的现货市场,但现货价格并不连续且存在区域性差异,现货价格的数据质量不高,所以在实证检验时本文将采用代理变量进行分析.用Fi，t来表示距离到期日还有i个月的期货合约在时刻t的价格.选用交割月期货合约价格（F1，t）作为现货价格（St）的代理变量,并利用距离到期日还有4个月的期货合约的价格（F4，t）和现货价格的代理变量,根据持有成本模型来倒推计算净便利收益率（δ=y-u）,即

其中利率r选取3个月期的SHIBOR利率1这里的利率是年化利率.由于SHIBOR利率数据在2006-10之前不可得,因此在此之前的利率数据采用3个月期的银行间回购加权利率.,利率和便利收益率均是年化的.

下面进行如下一系列的检验.利用式(4)所示的回归方程检验现货价格是否为均值回转过程.

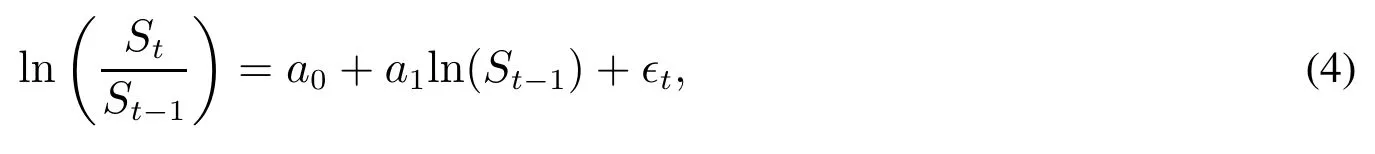
检验方程(4)中的回归系统系数a1是否显著不为零.这里利用现货价格的代理变量进行分析.进一步,检验铜期货现货价格是否近似满足Schwartz［36］提出的两因子模型.可以将两因子模型进行离散化的近似,即

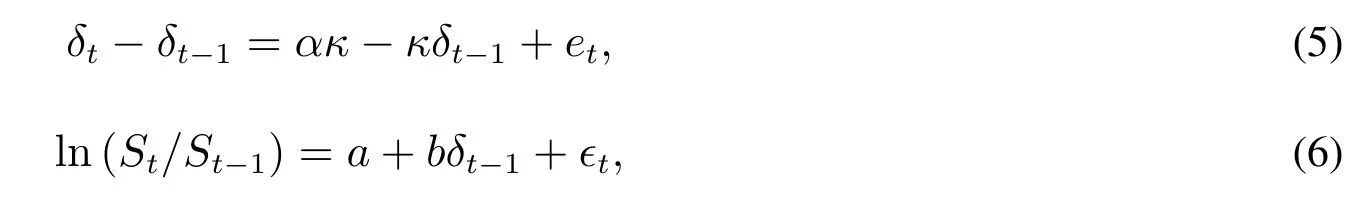
并且假设方程(5)和方程(6)的残差∈t和et相关,相关系数为ρ=corr（∈t，et）.

联立方程(5)和方程(6),利用似无关回归(seem ingly unrelated regression,SUR)方法对参数κ,α,a,b,ρ进行估计,并检验系数是否显著,以此确定两因子模型的设定是否适用于我国的铜期货合约.

在上述统计检验的基础上,构建包含现货价格（S）和净便利收益率（δ）的两因子模型,并假设这两个因子服从如下所示的联合随机过程

其中现货价格S的均值μ,波动率σ1,净便利收益δ的均值ακ和波动率σ2均为常数,并且d z1和d z2是相关的,有

Schwartz［36］指出,如果净便利收益率不是一个随机过程,而是基于现货价格的函数δ（S）=κln（S）,那么两因子模型就演化为设定现货价格是均值回转过程的单因子模型;如果净便利收益率是常数,模型就简化为Brennan等［30］的模型.

定义X=ln S,那么式(7)可写为

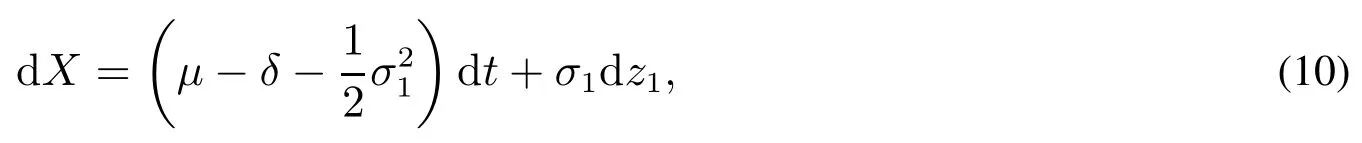
在等价鞅测度下,两因子模型可以写为

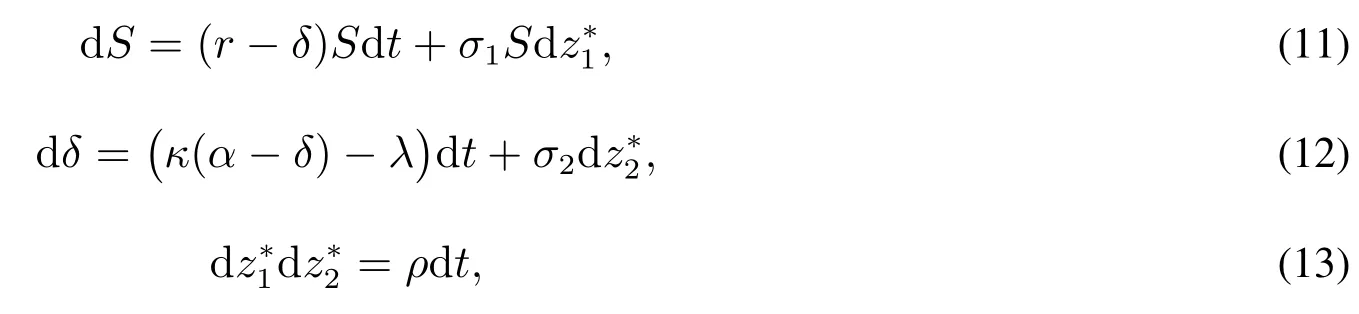
其中λ是便利收益风险的市场价格,通常假设为常数.而期货价格（F）则应该满足如下的微分方程

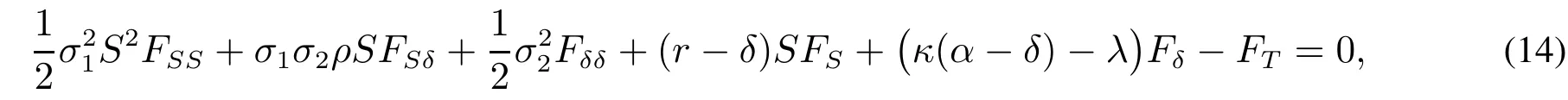
Schwartz［36］指出Jamshidian等［43］以及Bjerksund［44］已经给出了上述方程的解,即

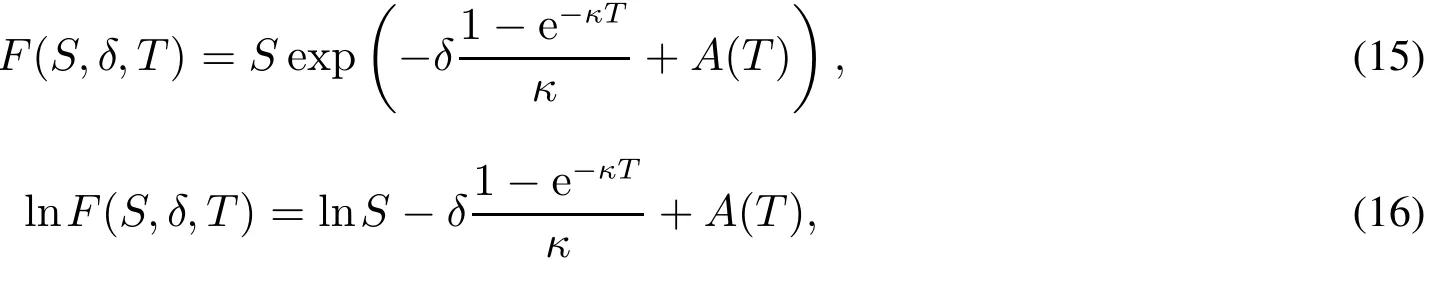
其中

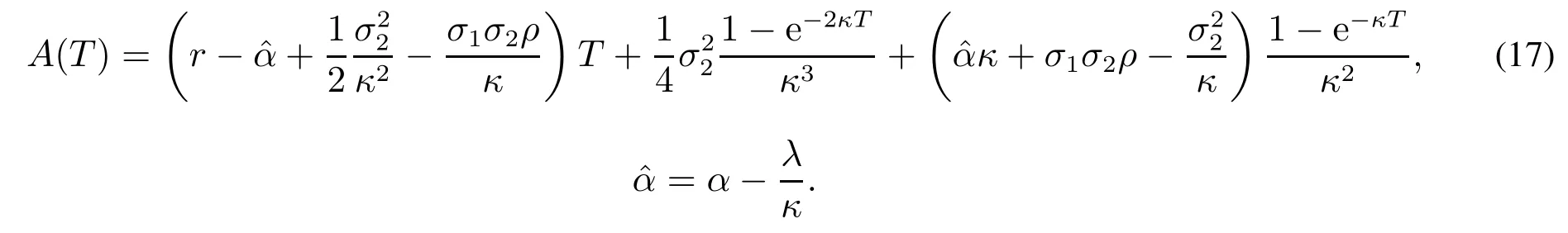
对于两因子模型的估计可采用状态空间模型和卡尔曼滤波方法.状态空间模型更有利于解决状态变量不可观测但已知其是一种Markov过程的情况.根据式(16)可以写出状态空间模型的度量方程(measurement equation);根据式(8)～式(10)写出状态空间模型的传递方程(transition equation)

其中t=1，2，...，NT.yt=（ln F（T1），ln F（T2），...，ln F（TN））T,是观测值向量;θt=（Xt，δt）T,是对数现货价格（Xt）和净便利收益率（δt）构成的状态向量.上述状态空间模型的度量方程中

4　数据和期货价格升贴水特征的统计检验

4.1数据和统计描述

本文的分析对象是上海期货交易所的铜期货,铜期货合约通常为每年1月至12月到期的12份期货合约.采集了2004-09-16—2012-12-14这段样本期内铜期货的所有历史合约的日度数据,共计2003个观测点.这段数据样本包含了铜期货于2004年至2006年间暴涨,受金融危机影响暴跌,并在金融危机后逐渐恢复至危机前的高价位运行的情况(如图1所示).因此,这段样本具有研究的代表性.本文以连续合约的收盘价表示不同期限的期货合约的价格.由于我国铜期货市场上交易最活跃的是距离到期日还有4个月的合约,而距离到期日最近的当月合约通常可用作现货价格的代理指标,那么这两份期货合约的价差（F4，t-F1，t）就比较好的反映了我国铜期货价格的期限结构特征,如图2所示.大多数时间两份合约价差小于零,尤其在2006年之前这种特征更是明显.

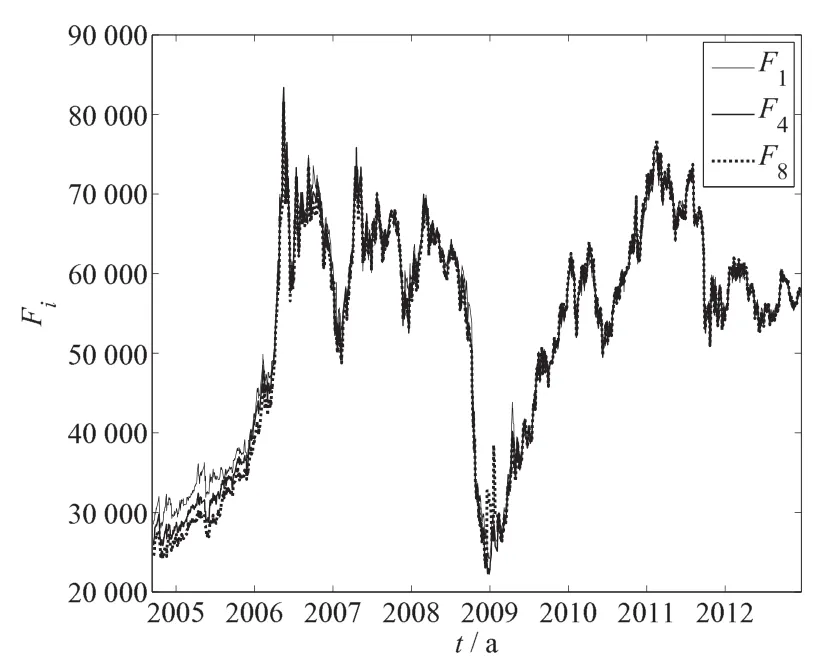
图1　铜期货合约价格走势Fig.1　Thehistorical pricesof different contracts of copper futures

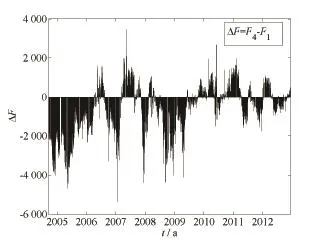
图2　铜期货F4合约与F1合约的价差Fig.2　The price spread between contract F4and F1of copper futures

本文对铜期货几份合约的价格序列进行了描述统计分析,如表1所示.

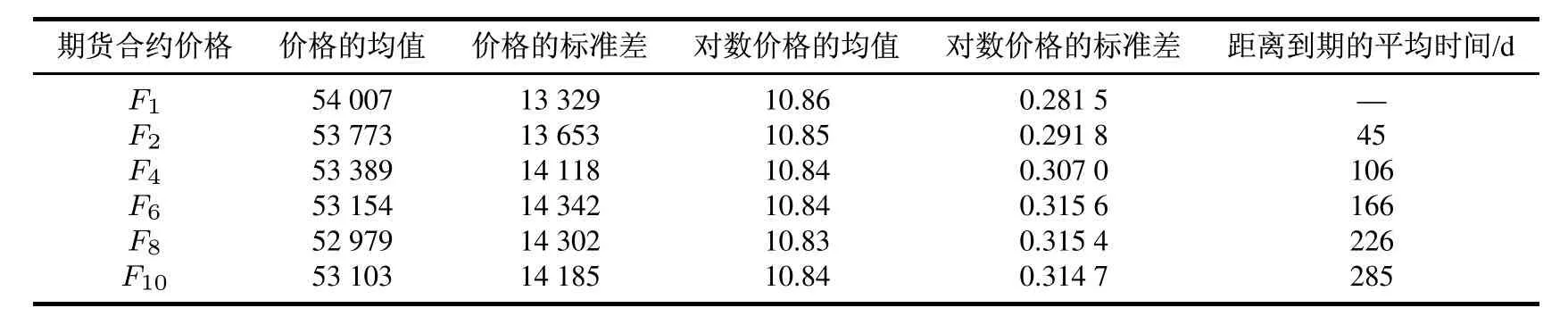
表1　铜期货不同合约价格的描述统计Table1　The descriptive statistics of copper futures contracts

表1显示,距离到期日越远的期货合约价格的均值越低且波动率越大.然而,距离到期日非常远的期货合约F8，F10出现了某种异常,F8虽然满足离到期日越远的合约价格越低的特征,但是波动率却反而减小了; 而F10的统计结果则完全与上述特征相悖.这两个合约价格的特征异常可能是由于这两份远月合约的交易不活跃造成的.若远月合约由于缺乏流动性而存在一段时间内没有交易的情况,那么数据记录则沿用上一个交易价格,这会使得所计算的价格波动率降低.基于这样的思考,虽然在后面的建模中仍保留了F8,但剔除了F10.

在无套利均衡的假设下,期货价格在到期日应等于现货价格.Kolb［12］提出Keynes［1］现货升水假设(normal backwardation)的一个核心推论就是,在到期日前期货价格会逐渐上升.这个推论可以表述为E［ln（Fi（tttm）/Fi（tttm+1））］＞0,或者E［Fi（tttm）-Fi（0）］＜0,这里tttm表示距离到期的时间.检验第一种表述,可计算其中RETi（tttm）=ln（Fi（tttm）/Fi（tttm+1））,l为该品种所有合约个数.检验第二种表述,可定义Di（tttm）=（Fi（tttm）/Fi（0））-1从而检验E［Di（tttm）］＜0,对所有tttm＞0成立.Kolb［12］指出检验后者比检验前者更为有效,且更适用于不同价位的期货品种.

本文所分析的中国铜期货的样本内,所有月份合约的对数日收益率的均值μ为5.587e–4,对原假设μ＞0的t–统计量为5.124 2,在5%的显著水平下显著.对于第二种表述,计算Di，t＜0的在所有样本中出现的频率占比为59.19%.这两个结果只能提供对于数据的最为粗糙的认识,仍需要进行更多检验.

4.2对现货价格和净便利收益率的序列性质检验

本文首先利用持有成本模型粗略计算了现货价格和净便利收益率的代理变量,并检验了序列性质.利用期货当月合约价格（F1）作为现货价格（S）的代理变量,并利用距离到期日还有4个月的期货合约价格（F4）,基于式(3)计算得到的净便利收益率（δ）.图3描绘了现货价格（S）、净便利收益率（δ）以及利率（r）和净便利收益率的利差（q=r-δ）.

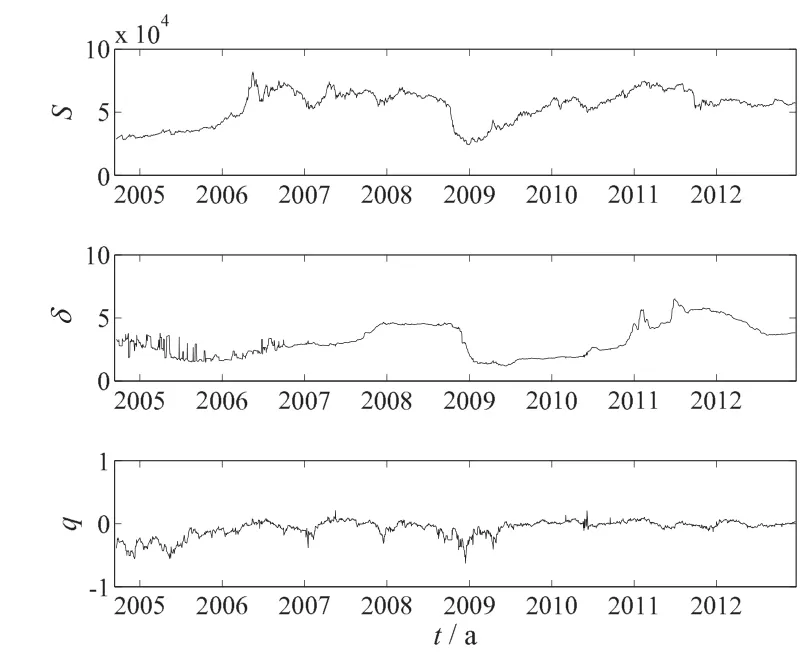
图3　利用代理变量计算的现货价格（S）,净便利收益率（δ）和利率与净便利收益率之差（q=r-δ）Fig.3　The spotprice（S）,convenient yield（δ）and the difference of the interest rateand netconvenience yield（q=r-δ）based on the proxy variables

对现货价格和净便利收益率两个序列建立如式(4)～式(6)的检验,结果如表2所示.

表2　现货价格对数收益率和便利收益率的性质检验Table2　The test resultsof log spotprice return and connivent yield

表2中第1行的结果显示现货价格对数收益率不是序列相关的;第二行的结果显示对数现货价格是一个均值回转的过程,因为方程的回归系数不为零且为负值.联立方程(5)和方程(6)并利用SUR估计,估计结果显示现货价格变化和便利收益率有关,便利收益率是一个均值回转的过程.这符合Schwartz［36］提出的两因子模型的假设.这里存在一个值得注意的问题,即在研究时间序列的微观特征尤其连续时间序列的特征时,回归的方法已经不再适用了,表2所示的回归方程拟合优度都很差就是这个原因.由此可见,需要建立连续时间过程的期货价格期限结构模型.

5　期货价格期限结构模型的实证结果

建立如方程(7)～方程(9)所示的期货价格期限结构的两因子模型,并用如方程(18)和方程(19)所示的状态空间模型和卡尔曼滤波来估计参数.这里,使用期货合约价格F2，F4，F6和F8来进行建模和参数估计.建模时所有数据均是年化数据,为此近似以260个交易日为一年换算Fi，t（T）中的t和T,即ta= t/260,t=1，2，3，...，2003,而T= （ti-t）/260,其中ti是某个期货合约的到期日,而t是当前观测时刻.在等价鞅测度下,设定无风险收益率r为0.03,接近代理变量利率的历史均值.估计时,设定误差容忍度为5×10-8,并设定最大迭代次数为3 000.参数稳定后（μ，σ1）=（0.7514，0.2726）,（κ，α，σ2，ρ）= （0.1796，0.2923，0.2500，0.2813）.上述参数全部都在5%的显著性水平下显著.等价鞅测度下,λ为0.0974.根据两因子模型得到的状态变量现货价格和便利收益率如图4所示.

图4所示的两因子模型估计的现货价格与图3所示的现货价格代理变量当月期货合约价格（F1）几乎一致.这与本文设定的模型容忍程度有关.并且,也说明利用当月合约（F1）作为现货价格的代理变量具有合理性.图4中由两因子模型估计的便利收益率与图3中用代理变量计算的便利收益率差别较大.这是因为我国的利率市场非市场化,很难获得无风险利率的代理指标,这使得图3所示的计算结果非常受限并且不准确.

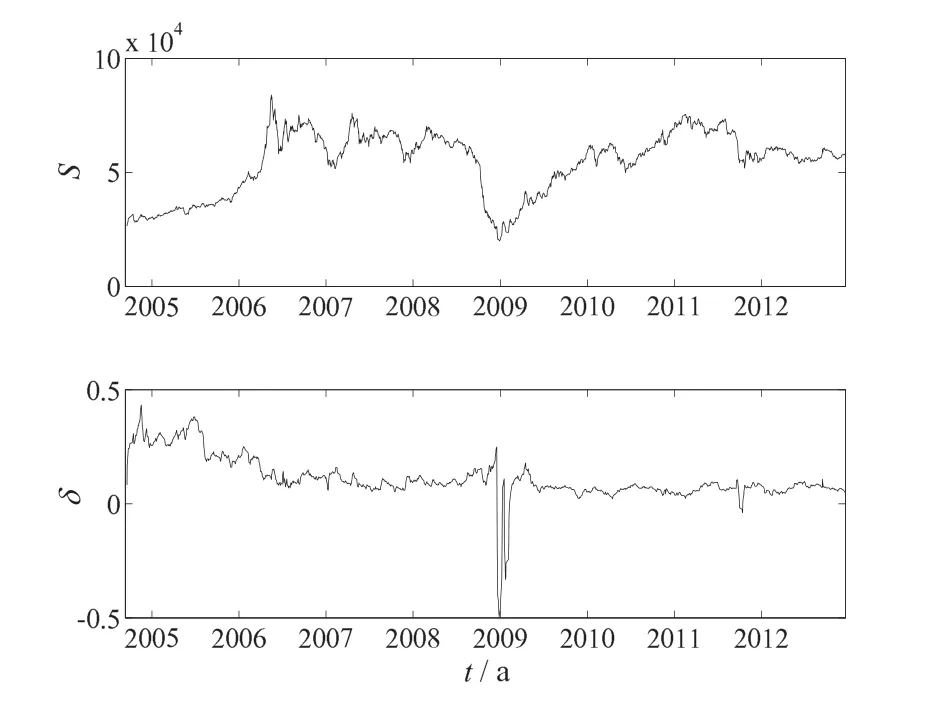
图4　两因子模型估计的状态变量现货价格和净便利收益率Fig.4　Two-factormodel’sestimation resultsof state variables-spot price and netconvince yield

从一定程度上讲,利用两因子模型来估计便利收益率更为合理.图4表明,在样本最开始的一段时间铜期货的便利收益率非常高,此后呈现逐渐降低的趋势,并曾在金融危机时期大幅下降呈现异常状态.本文计算了所估计的便利收益率的均值为0.110 4,便利收益率大于所设定的利率水平的观测点占总样本的97.45%.但是金融危机前后便利收益率与设定的利率水平的差异变化明显,金融危机之前便利收益率远大于利率,而金融危机之后二者的差异变得非常小.由此可见,铜期货价格虽然呈现现货升水特征,但是这种特征在金融危机前后有明显差别.

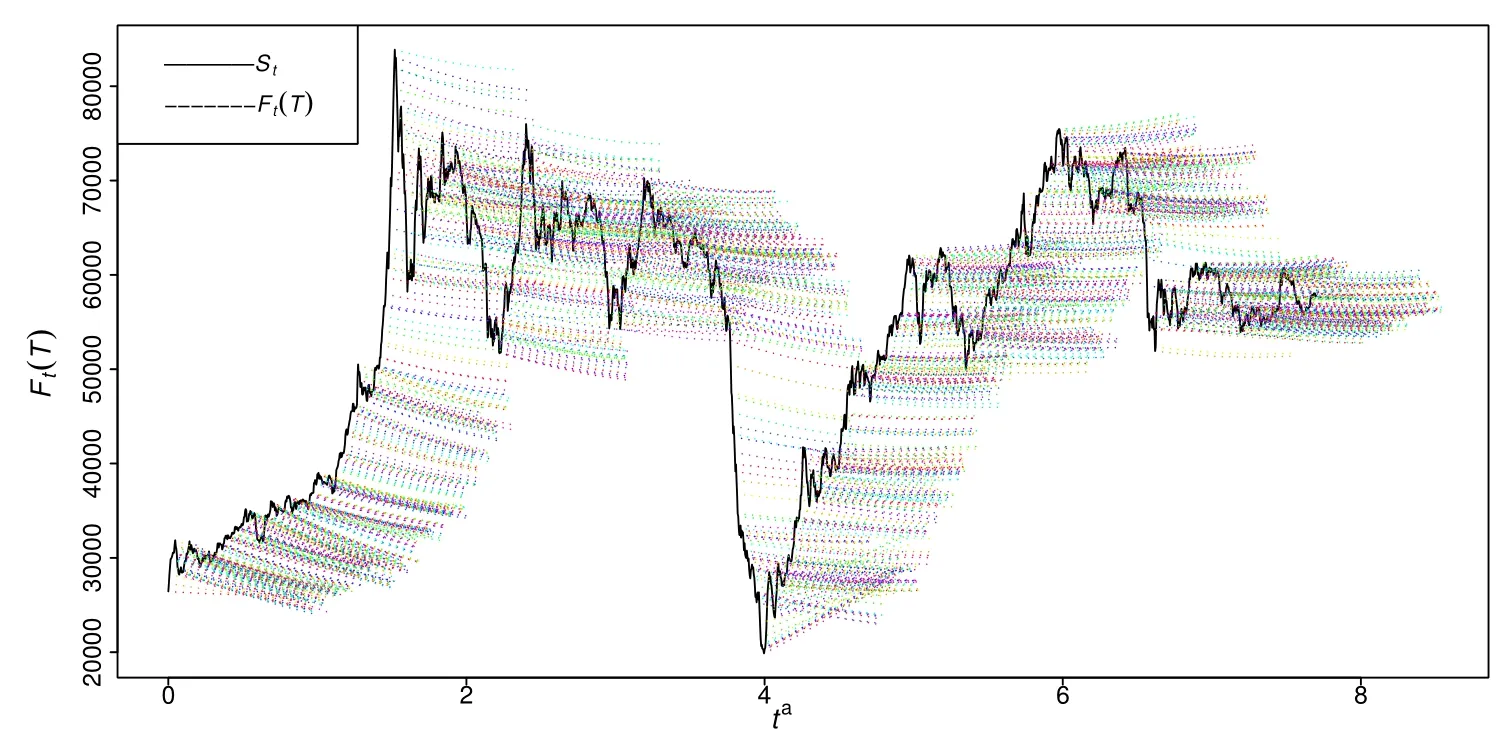
图5　两因子模型估计的远期价格曲线（ta=t/Z60,t=l，Z，3，...，Z003）Fig.5 Two-factor Modelgenerated forward price curves（ta=t/Z60，t=l，Z，3，...，Z003）

图5是基于两因子模型的估计结果拟合出不同时点上的远期价格曲线.由于两因子模型中所有变量均是年化数据,包括期货合约的到期时间T,所以图5横坐标是观测序列的时间轴,采用260个交易日为一年的方式进行年化,即ta=t/260,t=1，2，3，...，2003.远期价格Ft（T）中T的含义就是在任何时刻t看未来某个时刻ti到期的期货合约还能存续的时间长度,即图5中实线表示两因子模型所估计的每个时点的现货价格,而虚线表示每个时点所应对的不同期限的远期合约价格所构成的远期曲线.从图5中可以发现,起始时刻开始的1年内(即起始时刻到第260个交易日期间),远期曲线向右下倾斜程度更大,即现货升水(normal backwardation);而此后的近3年(大约780个交易日)中虽然远期曲线向右下倾斜程度减弱但仍然呈现现货升水.在距离起始时刻接近4年左右的时候(对应回日历日期为2008年金融危机时期)随着现货价格降至最低点,远期曲线出现非常明显的翻转,即远期曲线变为向右上倾斜,这说明这是出现了现货贴水(contango).随后很长一段时间,远期曲线近似于水平,并且偶尔有远期曲线向右上倾斜的情况出现.总的来说,我国铜期货市场在金融危机之前具有相对稳定的现货升水特征,尤其在2006年之前更为明显;我国铜期货市场在金融危机时期曾出现了现货贴水特征;金融危机之后很长一段时间,我国铜期货没有明显的现货升水或现货贴水;直至样本期最后,现货升水特征才逐渐恢复但仍然十分微弱.

6　结束语

本文利用上海期货交易所铜期货合2004-09—2012-12的数据,对其价格期限结构特征进行了研究.本文基于代理变量得到的现货价格和便利收益率,利用简单回归和SUR回归分析,证实了现货价格和便利收益率均是均值回转的过程,这也说明了Schwartz［36］提出的两因子动态模型适用于拟合我国的铜期货合约价格.因此,构建了两因子模型,并利用状态空间模型和卡尔曼滤波方法对参数进行了估计.利用两因子模型,估计得到了不可观测状态变量现货价格和便利收益率,拟合了不同时间点上的远期价格曲线.实证结果揭示了我国铜期货在金融危机之前具有相对稳定的现货升水特征,尤其在2006年之前更为明显;金融危机时期该特征曾发生异常逆转;危机过后较长一段时间铜期货市场无明显特征,近期现货升水特征逐渐恢复但仍很微弱.根据库存理论,便利收益率较高应与铜库存持续低位有关系,因而利用这种方法也可以间接推断影响期货定价的铜库存状态.

[1]Keynes JM.A Treatise on Money.Vol.2.London:Macm illan,1930.

[2]Hicks JR.Valueand Capital.Cambridge:Oxford University Press,1939.

[3]LautierD.Term structuremodelsof commodity prices:A review.Journalof A lternative Investments,2005,8(1):42–64.

[4]Frankfurter M M,Accomazzo D.Term Structure and Roll Yield:Not Your Father’s Backwardation.SSRNWorking Paper Series 1609776,2010.

[5]FuertesAM,M iffre J,RallisG.Tacticalallocation in commodity futuresmarkets:Combiningmomentum and term structuresignals. Journalof Banking&Finance,2010,34(10):2530–2548.

[6]Bernard J,Khalaf L,Kichian M,etal.Forecasting commodity prices:GARCH,jumps,andmean reversion.Journalof Forecasting, 2008,27(4):279–291.

[7]王苏生,王丽,李志超,等.基于卡尔曼滤波的期货价格仿射期限结构模型.系统工程学报,2010,25(3):346–353. Wang SS,Wang L,Li Z C,et al.A ffine term structuremodels of futures prices based on Kalman filter.Journal of Systems Engineering,2010,25(3):346–353.(in Chinese)

[8]王丽,王苏生,刘艳,等.中国期货价格期限结构模型实证分析.大连海事大学学报:社会科学版,2010,9(1):12–15,114. Wang L,Wang SS,Liu Y,etal.Empiricalanalysis on term structuremodelsof futuresprices in China.Journalof Dalian Maritime University:SocialSciences Edition,2010,9(1):12–15,114.(in Chinese)

[9]金璟,李水前,张毅,等.橡胶期货价格的期限结构及季节影响研究.云南农业大学学报:社会科学版,2012,6(1):57–61. Jing J,LiY Q,Zhang Y,etal.A study on influencesof term structure and seasonlity on China’snatural rubber future prices.Journal of Yunnan Agricultural University:Social Science Edition,2012,6(1):57–61.(in Chinese)

[10]Telser LG.Futures trading and the storageof cotton andwheat.The Journalof Political Economy,1958,66:233–255.

[11]Cootner P.Returns to speculators:Telser versusKeynes.The Journalof PoliticalEconomy,1960,68(4):396–404.

[12]Kolb R.Isnormalbackwardation normal.Journalof FuturesMarkets,1992,12(1):75–91.

[13]Lee JW,Zhang Y L.Evidenceon normalbackwardation and forecasting theory in futuresmarkets.JournalofDerivativesand Hedge Funds,2009,15(2):158–170.

[14]Dusak K.Futures trading and investor returns:An investigation of commodity market risk premiums.The Journal of Political Economy,1973,81(6):1387–1406.

[15]Carter C,RausserG,Schm itz A.Efficientassetportfoliosand the theory ofnormalbackwardation.The Journalof PoliticalEconomy, 1983,91(2):319–331.

[16]Marcus A.Efficientassetportfoliosand the theory of normalbackwardation:A comment.The Journalof Political Economy,1984, 92(1):162–164.

[17]Baxter J,Conine TE Jr,Tamarkin M.On commoditymarket risk prem iums:Additionalevidence.Journalof FuturesMarkets,1985, 5(1):121–125.

[18]EhrhardtM,Jordan J,Walking R A.An application of arbitrage pricing theory to futuresmarkets:Tests of normalbackwardation. Journalof FuturesMarkets,1987,7(1):21–34.

[19]M iffre J.Normalbackwardation isnormal.Journalof FuturesMarkets,2000,20(9):803–821.

[20]Houthakker H.Can speculators forecastprices.The Review of Econom icsand Statistics,1957,39(2):143–151.

[21]Rockwell C.Normal backwardation,forecasting,and the returns to commodity futures traders.Food Research Institute Studies, 1967,7(S):107–130.

[22]Chang E.Returns to speculatorsand the theory ofnormalbackwardation.Journalof Finance,1985,40(1):193–208.

[23]Kaldor N.Speculation and econom ic stability.The Review of Econom ic Studies,1939,7(1):1–27.

[24]Working H.Price relationsbetween July and Septemberwheat futuresatChicago since1885.WheatStudies,1933,9(6):187–240. [25]Carter C,Giha C.Theworking curve and commodity storage under backwardation.American Journalof Agricultural Economics, 2007,89(4):864–872.

[26]Gorton GB,HayashiF,RouwenhorstKG.The fundamentalsof commodity futures returns.Review of Finance,2013,17(1):35–105. [27]Deaton A,LaroqueG.On thebehaviourof commodity prices.Review of Economic Studies,1992,59(1):1–24.

[28]Pindyck R.The dynamicsof commodity spotand futuresmarkets:A primer.Energy Journal,2001,22(3):1–29.

[29]LinW T,Duan CW.Oilconvenience yieldsestimated underdemand/supply shock.Review ofQuantitative Financeand Accounting, 2007,28(2):203–225.

[30]Brennan M J,Schwartz ES.Evaluating natural resources investments.Journalof Business,1985,58(2):135–157.

[31]Gibson R,Schwartz E S.Stochastic convenience yield and the pricing of oil contingent claims.Journal of Finance,1990,45(3): 959–976.

[32]Gabillon J.Anaysing the Forward Curve:inManaging Energy PriceRisk London.London:Risk Publications,FinancialEngineering Ltd.,1995.

[33]Laughton D G,Jacoby H D.Reversion,timing options,and long-term decision-making.FinancialManagement,1993,22(3):225–240.

[34]Laughton D G,Jacoby H D.The effects of reversion on commodity projects of different length//Trigeorgis L.Real Options in Capital Investments:Models,Strategies,and Applications.Westport:Praeger Publisher,1995:185–205.

[35]RossSA.Hedging long run commitments:Exercises in incompletemarketpricing.Econom ic Notesby BancaMonte deiPaschidi Siena SpA,1997,26(2):385–420.

[36]Schwartz E S.The Stochastic behavior of commodity prices:Implications for valuation and hedging.Journal of Finance,1997, 52(3):923–973.

[37]Cortazar G,Schwartz E S.Implementing a real option model for valuing an undeveloped oil field.International Transactions in OperationalResearch,1997,4(2):125–137.

[38]Lautier D,Galli A.A term structuremodel of commodity priceswith asymmetrical behaviour of the convenience yield.Finéco, 2001,(11):73–95.

[39]Schwartz E,Sm ith JE.Short-term variationsand long-term dynam ics in commodity prices.Management Science,2000,46(7): 893–911.

[40]Cortazar G,Schwartz ES.Implementing a stochasticmodel foroil futuresprices.Energy Econom ics,2003,25(3):215–238.

[41]Casassus J,Collin D P.Stochastic convenience yield imp lied from commodity futuresand interest rates.Journalof Finance,2005, 60(5):2283–2331.

[42]Liu P,Tang K.The stochastic behaviorof commodity priceswith heteroskedasticity in the convenience yield.Journalof Empirical Finance,2011,18(2):211–224.

[43]Jamshidian F,Fein M.Closed form Solutions forOil Futuresand European Options in theGibson Schwartz Model:A Comment. Zurich:Merrill Lynch CapitalMarkets,1990.

[44]Bjerksund P.ContingentClaims Evaluationwhen the Convenience Yield isStochastic:AnalyticalResults.Sandviken:Institute for Foretaksøkonomi,Institute of Financeand ManagementScience,1991.

Study on backwardation and term structure of futures prices in Chinese copper futuresmarket

Bu Hui
(Schoolof Econom icsand Management,Beihang University,Beijing 100191,China)

Thispaperanalyzes thebackwardation characterof futurespricesin Chinesecopper futuresmarket. According to Kolb,the relationship between forward pricesand futures pricesatexpiration isexamined,and theexistenceof thebackwardation characterof copper futuresis tested.Using seemingly unrelated regression (SUR)analysis according to Gibson and Schwartz,the property of spot price and convenience yield based on the proxy variables is tested.It is found that both spot price and convenience yield are the processes with mean reverting.This illustrates that two-factor dynamic model of stochastic behavior of futures put forward by Schwartz is suitable for analyzing Chinese copper futures.Finally,a dynam icmodel is set up, which isestimated by thestate spacemodeland Kalman filtermethod.Theempirical results reveal thatnormal backwardationexistsinChinesecopper futuresbeforetheglobalfinancialcrisis,especiallybefore2006;and the characteronce reversed into contangoduring theperiodof financialcrisis.After financialcrisis,Chinesecopper futuresmarkethasno clearbackwardation or contango character fora long time;until recently,backwardation character recovergradually,but itis stillweak.

futuresmarket;backwardation;theory of storage;term structure dynam icmodel

F832.5

A

1000-5781(2016)02-0192-10

10.13383/j.cnki.jse.2016.02.005

2014-12-18;

2015-12-08.

国家自然科学基金资助项目(71003004;71373001);北京航空航天大学基本科研业务费资助项目(501000020-14108019;50100002015108001).

部慧(1981—),女,河北唐山人,博士,副教授,研究方向:期货市场,资产定价,风险管理等.Email:buhui@buaa.edu.cn.