基于HJM框架的随机波动率短期利率模型

陈志勇,江　良(.莆田学院管理学院,福建莆田3500;.莆田学院数学学院,福建莆田3500)

基于HJM框架的随机波动率短期利率模型

陈志勇1,江良2
(1.莆田学院管理学院,福建莆田351100;
2.莆田学院数学学院,福建莆田351100)

在Heath-Jarrow-Morton(HJM)框架下,建立随机波动率短期利率模型(ECIR-SV),其中长期均值为时间函数.基于重度取样技巧,利用Laplace方法和P–样条方法给出了ECIR-SV模型的极大似然估计方法.实证结果表明对比一些嵌入模型,ECIR-SV模型描述时间序列数据效果是最优的;对于单因子模型,引入长期均值函数的模型稍微地改善了拟合效果;在随机波动率模型中,考虑长期均值函数模型更好地描述短期利率动态变化.此外,通过长期均值函数能够更好地说明资本流动的情况,为宏观政策的制定提供了一些可靠的依据.

Heath-Jarrow-Morton模型;短期利率;随机波动率;Laplace近似;P–样条;长期均值

1　引　言

利率是金融市场活动中最重要的基础指标,其中短期利率显著地影响着固定收入证券定价和利率风险管理,如张连增等［1］基于CIR模型［2］给出水久性年金问题,孔文涛等［3］研究了随机利率下美式期权定价,这些说明短期利率模型能够影响到相应衍生品定价.因此,研究短期利率模型,特别是连续的模型,显得尤为重要.目前,研究短期利率模型可分为两类:单因子模型和多因子模型.虽然有大量实证表明,前者能够很好地刻画市场数据［2，4，5］,但很难描述对市场多变的期限结构形状.另一方面,对于单因子模型,不同期限的收益率相关系数为1,这种现象显然和实证证据相互冲突.因此,多因子模型应运而生.

Litterman等［6］首先考虑短期利率的波动率是随机的模型,他们认为随机波动率直接影响到利率的期限结构.同时,有研究者提出不同的随机波动率模型来研究短期利率的期限结构问题［7-9］,Ball等［10］应用不同国家市场数据论述了随机波动率模型的有效性.为了更好地拟合市场数据,Durham［11］探索了更一般的非线性随机波动率短期利率模型.郑挺国等［12］引入跳扩散因素来改善数据的拟合结果.Bali等［13］研究了非线性随机波动率模型,发现漂移项的变化也将改善拟合效果.Bikbov等［14］基于利率衍生品数据说明了随机波动率模型能提供更好的拟合效果.Li等［15］证明了多因子模型虽然能够很好地刻画债券数据,但不能对冲利率上限(caps)衍生品的风险.Andersen等［16］也发现随机波动率短期利率模型不能对冲零息债券的波动率,他们建议在模型中应该引入其他宏观经济变量.事实上,Li等［15］和Andersen等［16］所论述的模型和远期利率模型(HJM)［17］是不相容的,从而不能使用远期利率模型的衍生品对冲短期利率模型的波动率.因此,本文应用HJM框架下的随机波动率模型,使得该模型和HJM模型够相容.另一方面,基于HJM模型的短期利率衍生品定价是相当复杂的,因此有必要在此框架下使用短期利率模型来简化相应的衍生品定价的复杂性.

Hull等［5］在HJM框架下研究不同单因子的短期利率模型,他们得出引入长期均值函数的模型相容于HJM模型,并能够改善数据的拟合效果.Chiarella等［18］通过HJM模型推导更一般的单因子短期利率模型.上述短期利率模型即使能够很好地刻画市场数据,也无法解析短期利率变动的尖峰厚尾这一重要的特性,因为波动率是常数.Valchev［19］在HJM模型框架下给出了具有跳性质的随机波动率高斯模型. Filipovi´c等［20］通过远期利率模型也构建了高斯随机波动率短期利率模型.因为高斯模型可能产生负的利率,所以为了保证短期利率非负有必要研究非高斯的短期利率模型.

本文基于HJM框架建立随机波动率短期利率模型,其中长期均值是时间的函数,并通过实证分析模型的有效性.此模型充分地兼顾随机波动率和长期均值函数的两种性质,有力地解释尖峰厚尾现象,也能和远期利率模型相容.比较Hull等［5］模型,本文的模型具有随机波动率性质;而对比Valchev［19］模型,在合适的正则性条件下,本文模型所刻画的短期利率具有非负性质;相对于郑挺国等［12］模型,本文的模型和HJM模型相容,即长期均值为时间的函数.由于引入时间变量的系数和随机波动率因子,该模型的参数估计变得比较复杂.为了简化,本文使用两步估计方法,利用P–样条正则化方法［21］和模拟极大似然估计方法［22］进行参数估计和实证的分析.

2　随机波动率短期利率模型

本节基于HJM模型推导随机波动率短期利率模型,以实现该模型和HJM模型相容.

假设当前时刻t0=0,在无风险条件下,到期日为T的远期利率f（t，T）满足下面的随机微分方程

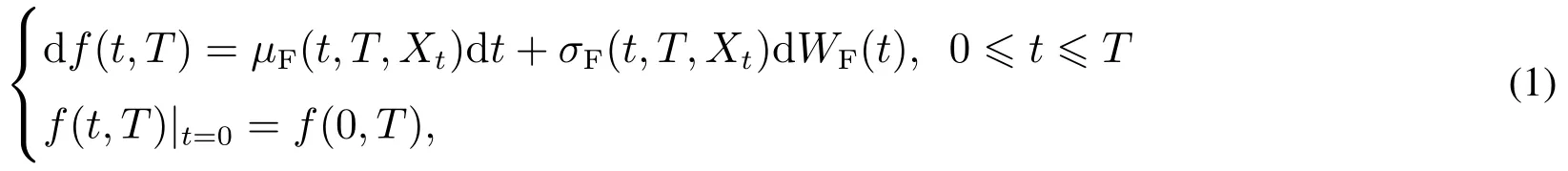
其中σF（t，T，Xt）是相应的波动率,Xt是与布朗运动WF（t）相互独立的连续的Markov链,漂移项为

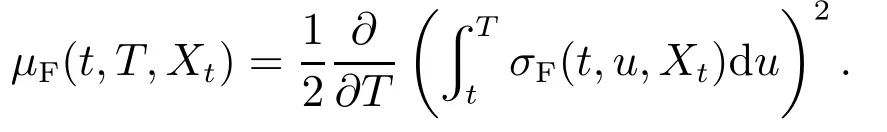
为了保证式(1)定义是有效的,假设σF（t，T，Xt）满足一些正则性条件［17］.

根据远期利率f（t，T）的定义,当T=t时,短期利率rt=f（t，t）.为了刻画短期利率rt的动态过程,需对式(1)积分,即

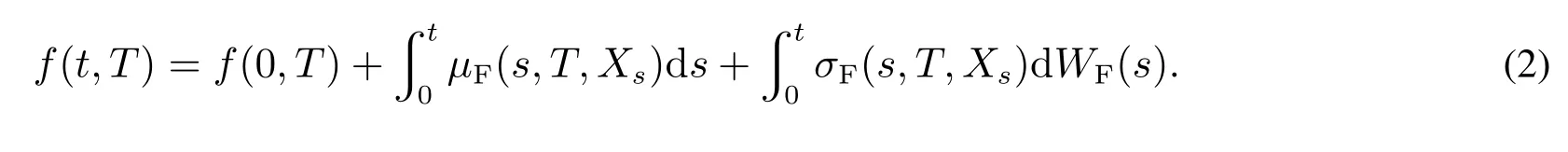
在式(2)中,设T=t,可得短期利率rt满足的积分方程

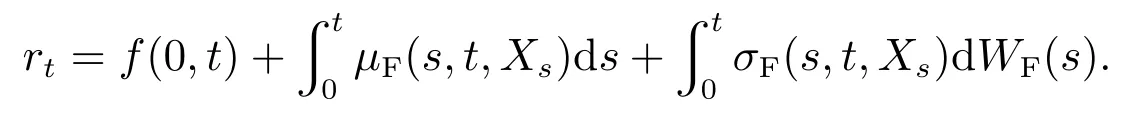
相应的随机微分方程为

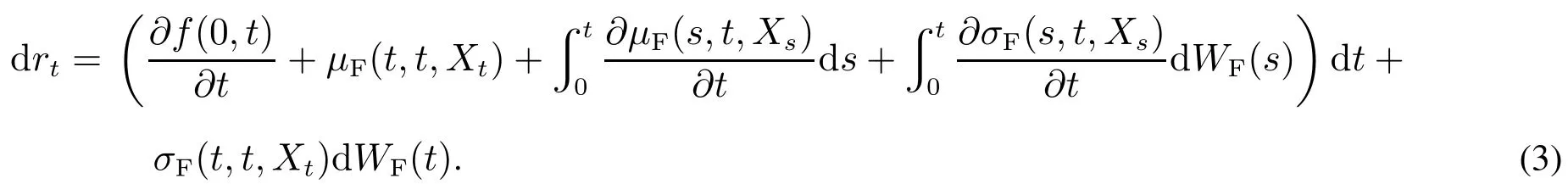
基于式(3),对于不同漂移项σF（t，T，Xt）的选取可得不同短期利率模型［5，18，19］.为了给出短期利率模型具有均值回归的性质,设σF（t，T，Xt）为1对于式(4),Cr´epey等［23］提出了更一般的假设,即σF（t，T，Xt）=g（r t，Xt）e-∫Ttψ（s）ds.但在此假设条件下,不影响本文的分析.

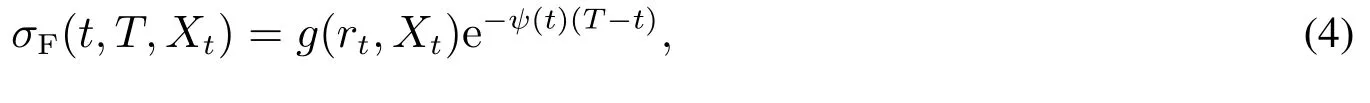
其中g（·，·）是一个确定的二元函数,ψ（·）是确定函数.

根据式(4),对σF（t，T，Xt）和μF（t，T，Xt）关于T的导数分别为

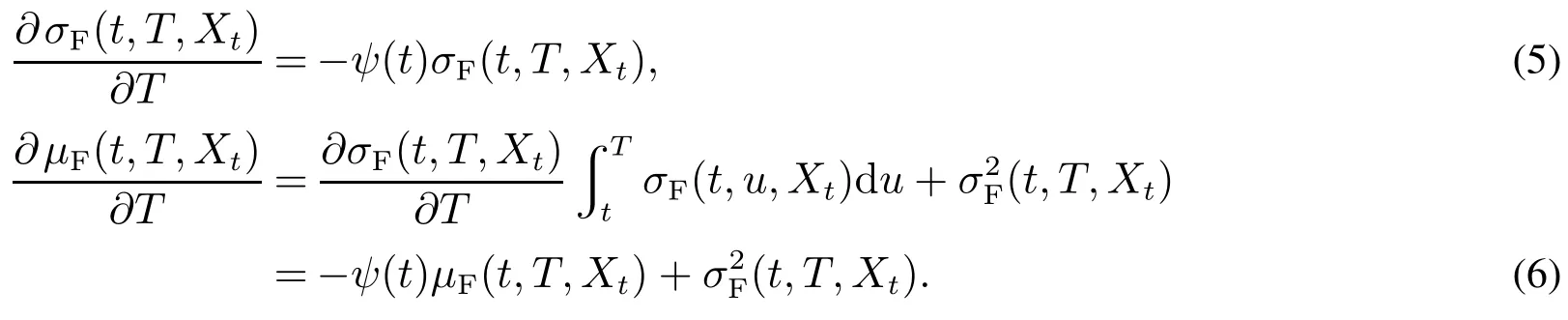
把式(5)和式(6)代入式(3),可得

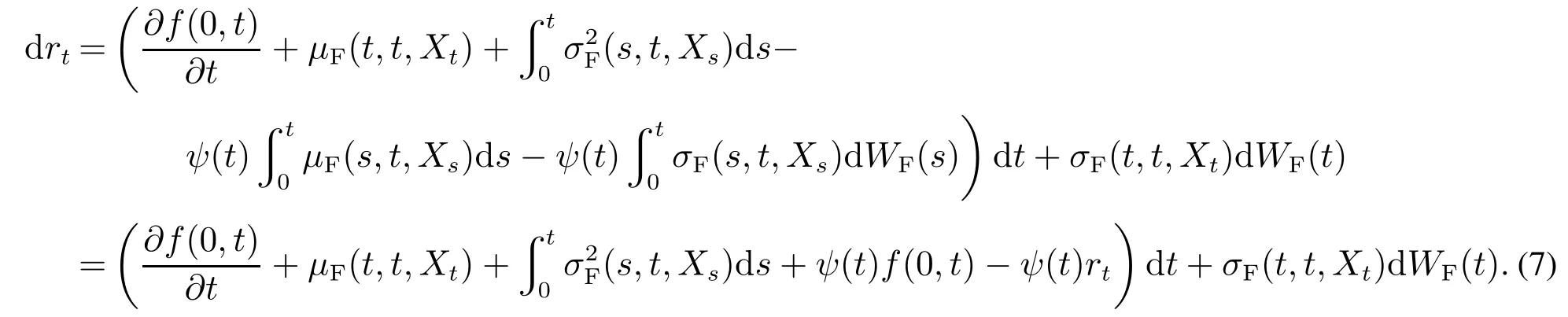
现在只需求σF（t，t，Xt）和μF（t，t，Xt）.基于式(4),可得

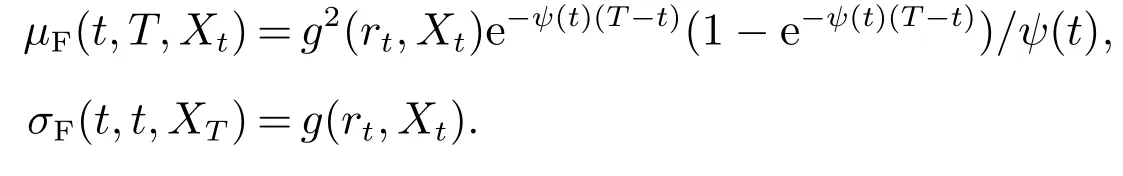
显然,μF（t，t，Xt）=0.为了保证短期利率非负,设

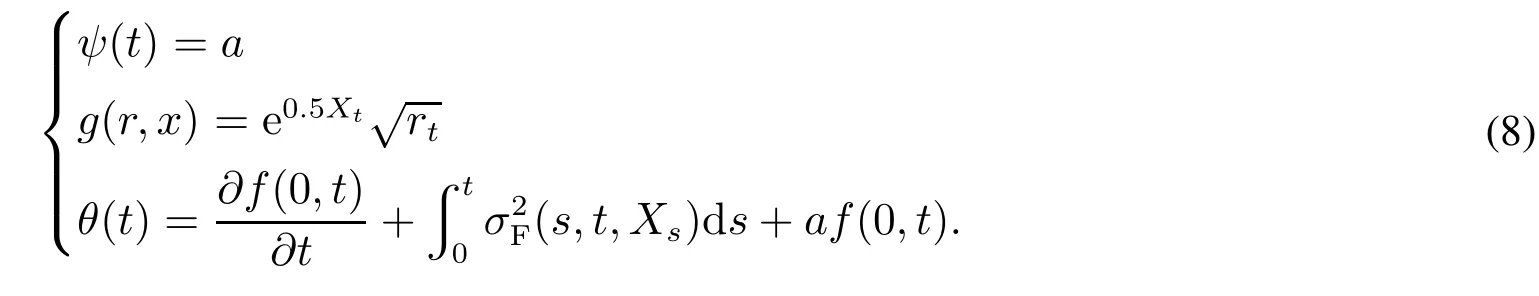
根据式(7)和式(8),可得下面的ECIR-SV模型,即随机微分方程

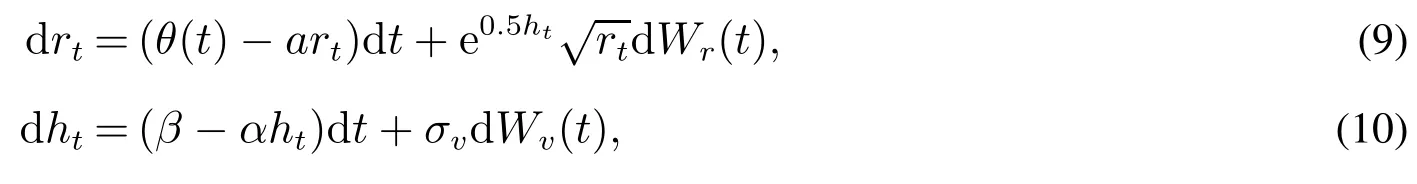
其中（Wr（t），Wv（t））是一对标准的布朗运动且E［d Wr（t）d Wv（t）］=0,2Ball等［10］通过实证方法论述了在随机波动率模型中,其相关系数ρ估计值几乎为零.Andersen等［16］基于零息债券数据给出短期利率水平的变化和波动率是不相关的.a和α分别是短期利率和波动率回归速率,θ（t）/a和β/α分别表示短期利率和随机波动率长期均值,σv是随机波动率的波动率.为了保证短期利率和随机波动率非负,ECIR-SV模型系数需要满足Feller条件,即给定ht条件下,2θ（t）≥eht.事实上,该条件可应用Fichera理论,仿照文献[24]第4章引理证明,当2θ（t）≥eht,式(9)确定的短期利率rt非负.

在ECIR-SV模型中,可通过设置参数得到一些著名的模型.如波动率e0.5若式(16)成立,密度函数尾部较厚,那么抽取较大随机数的概率较大,从而不影响重复模拟结果.ht=σ和θ（t）=θ是常数时,可得CIR模型［2］;若e0.5h t=σ是常数,可得ECIR模型［5］,即若θ（t）= θ,称该模型为CIR-SV［12］.

在ECIR-SV模型中,引入函数θ（t）不仅使得该模型和HJM模型相容,也能描述一些宏观经济现象对投资者长期期望利率的影响.比如,2008年经济危机时,虽然美联储通过降息的货币政策救市,但是投资者对这一货币政策的有效性产生怀疑.因此有理由认为投资者未来的期望利率不可能和过去值保持一样的.另一方面Hull等［4，5］也指出引入函数长期均值能够更好地剖析利率期限结构.

3极端条件下,θ（t）直接插值,那么数值结果和数据呈现一样的震荡.这种现象不利于利率衍品的定价,而且也很难预测参数未来的走向.　参数估计

为了实现模型的估计,首先应用Euler离散格式将ECIR-SV模型转化为离散方程.设Δt=ti-ti-1，i= 1，2，...，N,ri和hi分别表示相应在ti时刻的离散值,θi=θ（ti）.式(9)和式(10)的离散方程分别为

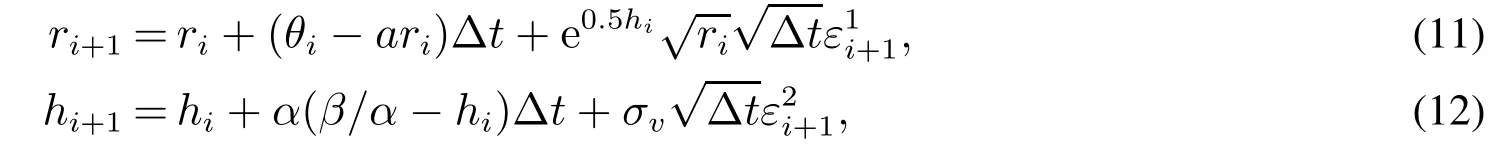
由于波动率是不可观测的,基于时间序列数据,似然函数为

最大化式(13)需要处理两个问题:1)式(13)是一个高维的积分方程,一般没有解析表达式;2)直接最大化式(13)可能得到一些不稳定的数值解Θ,3极端条件下,θ（t）直接插值,那么数值结果和数据呈现一样的震荡.这种现象不利于利率衍品的定价,而且也很难预测参数未来的走向.须进一步考虑对θ（t）估计的稳定算法.为了解决这两个问题,分成两个步骤求解,首先考虑式(13)的积分问题,然后再应用P–样条正则化方法估计θ（t）.

3.1积分Laplace近似方法

由于式(13)是高维积分,因此应用模拟最大似然估计方法(SMLM)估计式(13)中的常系数.这里采用重度取样方法估计式(13)积分积分的值,即

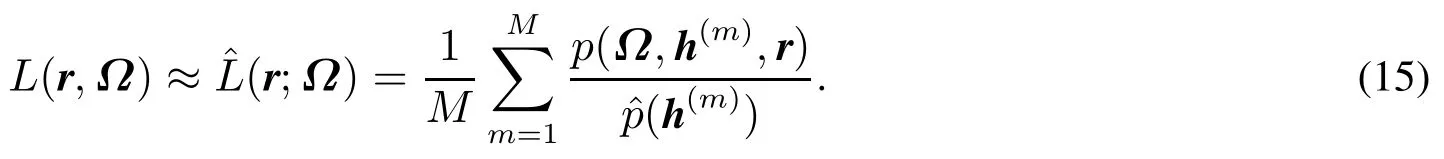
式(16)不仅保证了收敛性而且也保证了重复抽样方法的有效性.5若式(16)成立,密度函数尾部较厚,那么抽取较大随机数的概率较大,从而不影响重复模拟结果.显然对于密度函数的选取直接影响到

式(15)近似的数值结果.根据Huang等［22］和Durham［28］的研究,为了给出密度函数,基于La p l a c e近似方法,选取其中N（·，·）表示正态分布, H*是Hesse矩阵H在h*上的取值,关于Laplace近似方法的分析可参考文献[30].

步骤1给定参数Ω的初值条件;

步骤2根据步骤1初值条件通过牛顿迭代方法给出h*;

步骤3将步骤2的结果,代入式(15)求出相应参数的估计值;

步骤4返回步骤1直到收敛结束.

下面给出计算优化问题(17)的方法.基于式(11)和式(12)的离散格式,有

式(19)的求解可应用牛顿迭代法,即

其中h（0）表示给定的初始条件,Hesse矩阵6Huang等［22］给出2阶Taylor展开近似e-hi,从而减小计算量.但是对于本文的问题,|hi|可能取值较大,这就导致其2阶近似误差比较大.因此将直接通过牛顿方法求解方程(19).

3.2P–样条函数

本文将选取P–样条正则化方法估计函数θ（t）,以便获得稳定的数值结果.其主要原因是P–样条正则化方法既能够刻画回归函数尖峰性质(sharp features)又能保持回归函数的光滑性,而且使用P–样条方法的近似有利于统计假设检验［31］.

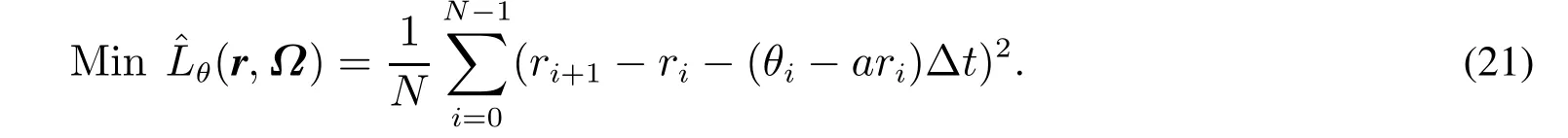
显然,式(21)的极小元为θiΔt=ri+1-（1-aΔt）ri,但是这类解可能和短期利率呈现一样的震荡.因此,有必要利用P–样条正则化方法求解.基于P–样条函数,θ（t）近似为

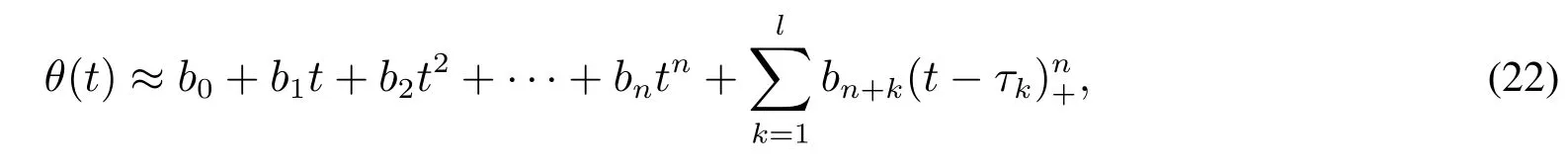
根据Jarrow等［32］和Yu等［21］的研究,一般选取二次样条(quadratic spline)函数作为基函数,其原因是真实均值函数的一些性质是未知的,而使用二次样条函数逼近会保持回归函数具有一定的尖峰性质.事实上,在二次样条下,Ruppert［33］通过模拟方法给出l应在5～10之间最优,特别是Jarrow等［32］通过数值测试发现l选取8～10为最佳取值.而对于节点τk,将应用Ruppert［33］方法,即,τk选择在k/（l+1）分位点上.因此本文取n=2，l=10.

在P–样条近似条件下,关于θ（t）的优化问题可转化为

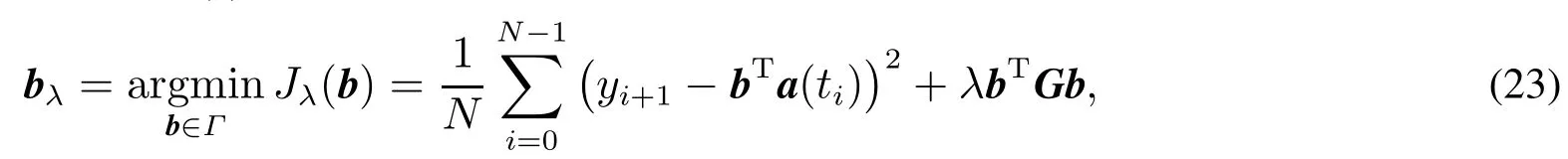
对正则化参数选取将使用GCV(generalized crossvalidation)方法［34］.设RSS（λ）为

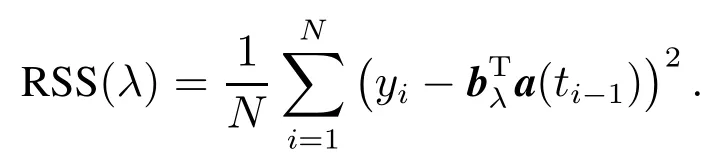
基于GCV方法,正则化参数通过求下面表达式极小值获得,即

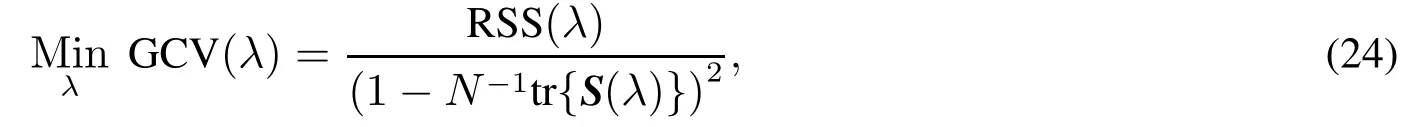
其中tr（·）是矩阵对角元素和,S（λ）是广义影响矩阵(generalized influencematrix).根据Sima等［35］研究结果,矩阵S（λ）的元素为

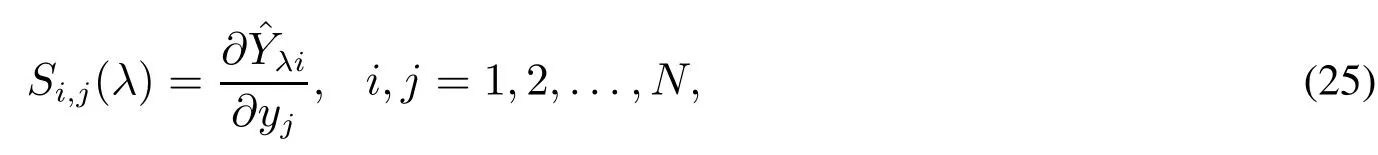
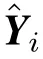
步骤1给定一个初值ω0,b0;

步骤2求优化问题(17),进一步给定b0,从优化问题(15)求解

步骤4重复步骤2和步骤3直到收敛.

根据算法可得

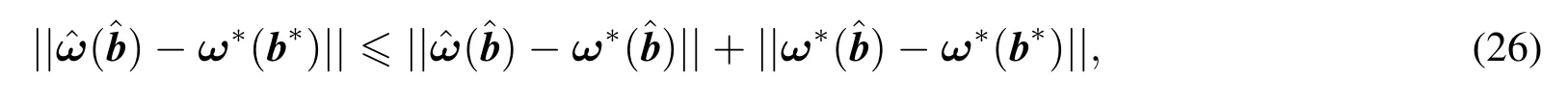
其中ω*和b*表示相应的真实值.

显然在一定正则性假设条件下,只需证明算法中步骤2和步骤3收敛,那么算法就收敛.关于算法步骤2和步骤3的正则性假设及相容性性质分别可以参考文献[21,30].式(26)也揭示了选择合适的初值将会加速收敛速度.对初值问题ω0的选取,直接通过CIR-SV模型估计获得,即

而对于b0,通过ECIR模型参数估计获得.另一方面,采用两阶段估计:1)通过优化问题(27)给出初值ω0;2)运行上述算法一次即可获得估计结果.

4　实证

由于我国债券数据不完整,为了统计分析的可行性,本文将使用美国债券数据.在市场上短期利率是不可观测的,本文将使用每周交易3个月到期零息债券收益率近似,时间间隔为2000-01-07—2012-06-01,总的数据为648个(数据来源于http://www.ustreas.gov),相应的时间步长Δt=1/52.8Longstaff等［9］和Durham［11］也应用3个月到期零息债券收益近似短期利率.

根据Shephard等［36］研究,为了减少计算量,在计算式(15)时,选择M=64个样本,重复抽样1000次,9Huang等［22］和Durham［28］通过模拟方法验证了在重度取样过程中,取64个样本重复抽样1000次能够获得精确的参数估计值.而且他们也提出为了进一步减少计算量,在应用牛顿迭代算法时可以选择固定迭代次数.如Huang等［22］设6次迭代.但是在本文算法中,不需要设置牛顿迭代次数,因为每次牛顿迭代次数大约在6次左右就收敛.

为了诊断模型的有效性,本文应用似然比检验(LR).10另一种可性性方法是通过样本之外测试.若假设使用一步向前预测(one-step-ahead),根据最小二乘法原理,显然预测值最优的估计为i+1=E［ri+1|Fi］=E［E（ri+1|hi，Fi）Fi］,其中Fi表示在ti之前所有信息.从这个预测方程可知,需要对于随机波动率进行预测.注意这里随机波动率是不可观测,因此对于不可观测随机波动率预测问题将是在将来继续研究的问题.但是作为一个结果,发现A¨ıt-Sahalia等［40］仅使用似然率就足够测试了模型的有效性.因此仅仅考虑似然率检验.对于全参模型,设L（Θ，h）和~L（Θ，h）分别为无约束条件和有约束条件的似然值,似然比为

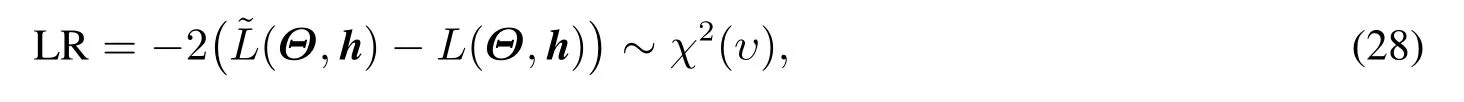
其中υ是约束条件的个数.

通过式(28)的数值与相应的χ2分布的临界值比较,可以判断是否拒绝给定的约束条件的假设.

对于半参模型,根据Ciprian等［37］研究,若选取二次P–样条,似然率检验为自由度1的χ2分布,即检验下面的假设

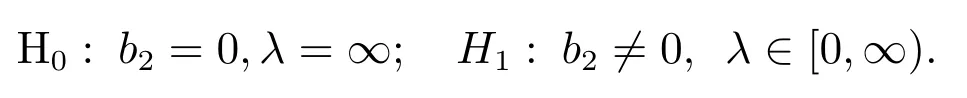
另一方面,根据参数估计的要求,定义下面的残差

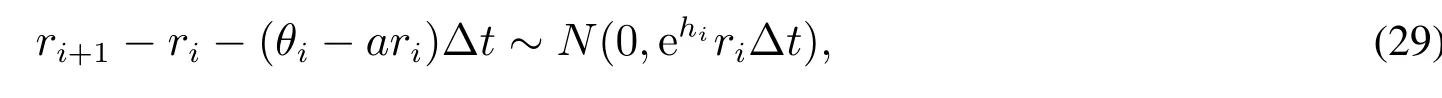
式(29)基于条件概率分布,即给定波动率条件下相应的残差服从正态分布函数.

由于随机波动率是不可观测的,因此需要给出相应的估计替代.根据文献[39]的附录,有

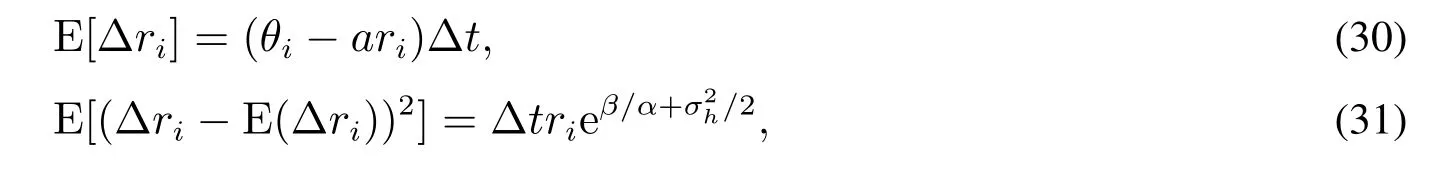
其中E［·］是期望算子,式(30)和(31)分别表示Δri的期望值和波动率的估计,它们的合理性及统计性质可参考文献[41].

表1列出不同模型参数估计值和相应的似然函数值.对于CIR模型,长期均值为θ/a=0.022 7,Feller条件2θ/σ≥1.

表1　不同模型的参数估计值Table1　Parametersestimating value for the differentmodels

从表1中的数据可以看出,当不考虑长期均值函数时,其回归速率α值较小,这说明了全参模型的利率水平具有较强的持续性想象.另一方面,随机波动率比长期均值函数对似然值影响比较大,这说明随机波动率对于短期利率水平冲击较大.CIR-SV和ECIR-SV模型随机波动率长期均值β/α分别为-4.043 3和-4.089 9,这两个值几乎是相近的,说明了长期均值函数不影响随机波动率的长期均值.此外,从表1最后一列数据可以看出,似然函数值是递增的.这表明了引入长期均值函数和随机波动率都可改善拟合的效果.

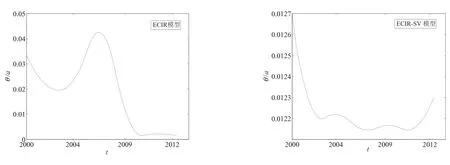
图1　应用P–样条函数方法所得θ/a的估计值.Fig.1 Thenumerical resultsθ/a by using GCV method

图1画出ECIR和ECIR-SV模型长期均值函数形状.从图1可以看出,不考虑随机波动率时,在2009年之前长期均值被高估.这就说明随机波动率直接冲击长期均值的变化.此外,大约在2009年之后,两个模型所对应的均值趋势完全不同.从实际情况考虑,ECIR-SV模型更能体现资本流动情况.如,在2000—2003和2004—2008期间,受到上个世纪末互联网泡沫和次贷危机的影响,投资者对于市场失去信心而更愿意持有政府所发行的金融产品(债券等)作为投资,这就导致更多资本涌入债券市场,那么驱使债券价格持续向上,从而导致收益率减小,相应的长期收益就呈现递减趋势.在2003—2008和2010—2012期间,美联储使用宽松货币政策刺激经济,投资者对于市场恢复了信心,资本从债券市场向其他投资市场流动,债券价格就具有下降趋势,那么长期期望收益就有递增的趋势.

表2给出了相应的似然率统计量检验.从表2的数据可以看出,显然CIR模型拟合效果最差,而ECIRSV模型拟合效果最好.另一方面从似然比统计检验也可以看出,随机波动率比长期均值函数对于模型的影响较大.通过引入长期均值函数,相应的模型也改善了拟合效果.

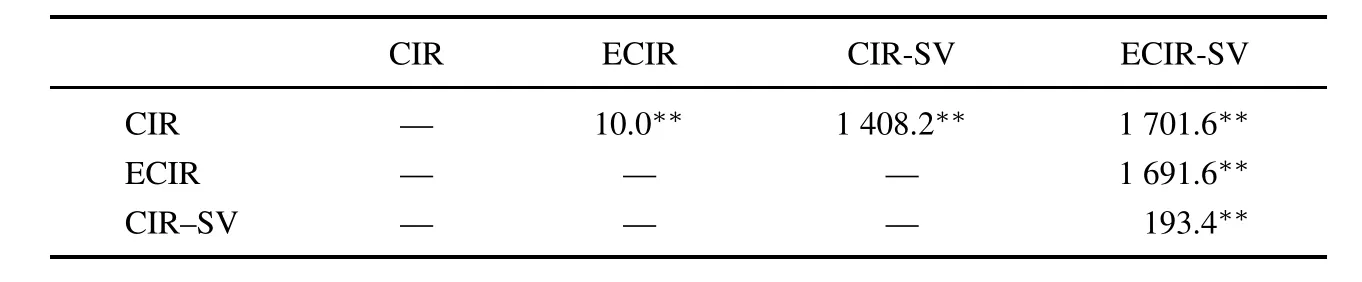
表2　不同模型之间似然率LR估计值Table 2 Log-Likelihood ratio for the differentmodel

图2给出不同模型的残差正态分布图.从图2可以看出,所有的模型残差和正态分布函数是有区别的,特别是尾部的事件.这说明了可能需要引入其他的因素来改善模型,如Eraker［38］论述,引入跳因素模型,可以很好地捕获尾部的事件.此外,随机波动率模型将也改善了残差,从而进一步验证两因子模型比单因子模型更具有解释力.

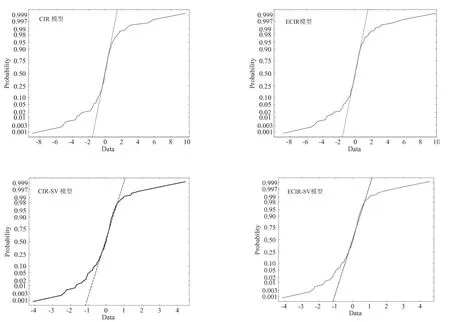
图2　不同模型的残差正态分布QQ图Fig.Normality QQ plotof the residuals for each of themodels

图3描述不同模型期望值的估计从图3可以看出,每个模型都具有光滑的估计,而且似乎E C I R模型所得估计最优.然而根据表2中的数据可知,似然率检验拒绝ECIR模型.因此不能根据估计的光滑性来判断模型的有效性.例如在一种极端条件下,使用Lagrange插值方法给出Δr的估计,也就是所得曲线在每个节点

上完全和Δr等同,相应的波动率为零.显然这是不合理的估计,因为利率是随机的.这就说明需要光滑的估计,而图3刚好说明这个问题.

图4描述不同模型期望值和波动率的估计.观察图4,大约在2001年或2008年前后,基于CIR-SV模型所得估计可能高估了,而在其他时间上两个模型几乎是相同的估计.这个结果是不矛盾的,因为从表2数据可以看出,对比随机波动率和长期均值对似然率的影响,显然随机波动率对似然率贡献较大.因此,在短期利率模型中引入长期均值函数会影响到利率动态变化,但不如引入随机波动率对模型影响那么大.

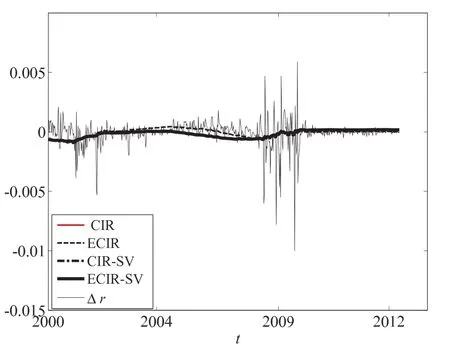
图3　基于式(30),增量Δr期望值的估计Fig.3 Estimation forexpected value ofΔr by equation(30)

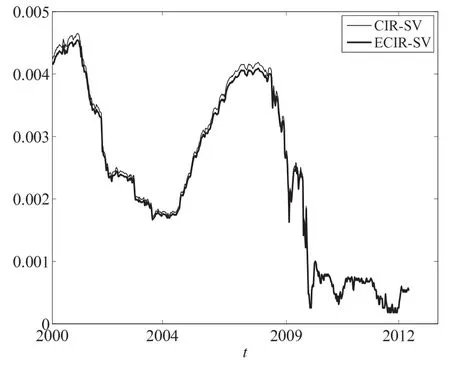
图4　基于式(31),增量Δr波动率的估计Fig.4 Estimation for volatilities ofΔr by equation(31)

5　结束语

虽然很多全参短期利率模型能够很好地刻画市场数据,但是它们很难描述和解释一些重大事件与投资者长期期望利率的关系.这些模型也无法和远期利率模型(HJM)相容.因此本文在CIR模型基础上引入随机波动率和长期均值函数的模型,从而更好地挖掘市场数据以及解释一些重大事件和政策对于投资者长期期望利率的影响,同时也实现了和HJM模型相容.由于随机波动率是不可观测的以及长期均值是时间的函数,相应的似然函数计算变得比较困难.为了解决上述问题,本文利用Laplace近似方法和P–样条方法并使用重度取样技巧展开极大似然估计.实证结果表明了ECIR-SV模型的拟合效果最好,而全参的模型拟合效果较差.此外引入时间均值能够更好地解释一些重大的事件对资本流动情况的作用,如上个世纪末互联网泡沫和2008年次贷危机发生后的美联储货币政策.另一方面,实证结果也表明了随机波动率比长期均值函数对于短期利率的影响要大,而且随机波动率和长期均值函数还无法完全反映短期率利率动态变化(见图2).因此进一步研究可能需要考虑一些其它宏观变量或跳的因素对于短期利率的影响.

[1]张连增,段白鸽.CIR利率模型下水久年金现值变量的分布模拟.系统工程学报,2014,29(1):56–65. Zhang L Z,Duan B G.Simulation of the presentvalue of perpetuity in CIR interestmodel.Journalof Systems Engineering,2014, 29(1):56–65.(in Chinese)

[2]Cox JC,Ingersoll JE,Ross SA.A theory of the term structure of interest rates.Econometrica,1985,53(2):385–407.

[3]孔文涛,张卫国.带跳市场中随机利率下的美式-亚式期权定价.系统工程学报,2012,27(3):338–343. KongW T,ZhangW G.American-style asian option pricingwith jumpsunderstochastic interest rate.Journalof SystemsEngineering,2012,27(3):338–343.(in Chinese)

[4]Hull J,White A.Pricing interest-rate-derivative securitites.The Review of FinancialStudies,1990,3(4):573–392.

[5]Hull J,White A.One-factor interest-ratemodeland the valution of interest-rate derivative securities.Journalof Financialand Quantitative Analysis,1993,28(2):234–235.

[6]Litterman R,Scheinkman JA.Volatility and yield curve.Journalof Fixed Income,1991,1(1):49–53.

[7]Andersen TG,Lund J.Estimating continous-timestochastic volatiltymethodsof theshortterm interestrate.JournalofEconometrics, 1997,77(2):343–377.

[8]Fong G H,Vasicek O A.Fixed-income volatilitymanagement.Journalof Portfolio Management,1991,7(4):41–46.

[9]Longstaff FA,Schwartz E.Interestrate volatility and the term structure:A two-factorgeneralequilibriummodel.Journalof Finance, 1992,47(4):1259–1282.

[10]BallCA,TorousW N.The stochastic volatility of short-term interest rates:Some internationalevidence.Journalof Finance,1997, 54(6):2339–2359.

[11]Durham GB.Likelihood-based specification analysisof continuous-timemodelsof the short-term interest rate.Journalof Financial Economics,2003,70(3):463–487.

[12]郑挺国,刘金全.随机波动和跳跃下的短期利率动态.系统工程理论与实践,2012,32(11):2372–2380. Zheng T G,Liu JQ.Short rate dynamics with stochastic volatilities and jumps.System Engineering:Theory&Practice,2012, 32(11):2372–2380.(in Chinese)

[13]Bali TG,Wu L A.Comprehensive analysis of the short-term interest-rate dynamics.Journalof Banking&Finance,2006,30(4): 1269–1290

[14]Bikbov R,Chernov M.Yield curve and volaility:Lessons from eurodollar futures and options.Journalof Financial Econometircs, 2011,9(1):66–105.

[15]LiH,Zhao F.Unspanned stochastic volatility:Evidence from hedging interest rate derivatives.The Journalof Finance,2006,61(1): 341–378.

[16]Andersen T G,Benzoni L.Do bonds span volatility risk in the U.S.treasury market:A specification test for affine term structure models.Journalof Finance,2010,65(2),603–653.

[17]Health D,Jarrow R,Morton A.Bond pricing and the term structure of interest rates:A new methodology for contingent claims valuation.Econometrica,1992,60(1):77–105.

[18]Chiarella C,Kwon OK.Classesof interest ratemodelsunder theHJM framework.Asia-Pacific FinancialMarkets,2001,8(1):1–22. [19]Valchev S.Stochastic volatility Gaussian Heath-Jarrow-Mortonmodels.Applied Mathematical Finance,2004,11(4):347–368.

[20]Filipovi´c D,Trolle A B.The term structure of interbank risk.Journalof Financial Econom ics,2013,109(3),707–733.

[21]Yu Y,RuppertD.Penalized spline estimation for partially linear single-indexmodels.Journalof The American Statistical Association,2002,97(460):1042–1054.

[22]Huang S J,Yu J.An efficientmethod formaximum likelihood estimation of a stochastic volatility model.Statistic and Inference, 2008,1(2):289–296.

[23]Cr´epey S,Nguyen H,Grbac Z.A multiple-curve HJM modelof interbank risk.Mathematics and Financial Econom ics,2012,6(3): 155–190

[24]姜礼尚,徐承龙,任学敏,等.金融衍生产品定价的数学模型与案例分析.第2版.北京:高等教育出版社,2013. Jiang L S,Xu C L,Ren X M,etal.MathematicalModelsof Financial Derivatives Pricing and Case Analysis.2nd Edition.Beijing: Higher Education Press.(in Chinese)

[25]吴鑫育,马超群,汪寿阳.随机波动率模型的参数估计及对中国股市的实证.系统工程理论与实践,2014,34(1):35–44. Wu X Y,Ma C Q,Wang S Y.Estimation of stochastic volatility models:An empirical study of China’s stock market.System Engineering:Theory&Practice,2014,34(1):35–44.(in Chinese)

[26]吴鑫育,周海林,马超群,等.基于EIS的杠杆随机波动率模型的极大似然估计.管理科学学报,2013,16(1):74–86. Wu X Y,Zhou H L,Ma C Q,etal.EIS-based maximum likelihood estimation of stochastic volatility modelwith leverage effect. JournalofManagement Sciences in China,2013,16(1):74–86.(in Chinese)

[27]Richard JF,ZhangW.Efficienthigh-dimensional importance sampling.Journalof Econometrics,2007,141(2):1385–1411.

[28]Durham G B.MonteCarlomethods forestimating,smoothing,and filtering one-and two-factor stochstic volatilitymodels.Journal of Econometrics,2006,133(1),273–305.

[29]Koopman SJ,Shephard N,Creal D.Testing the assumptionsbehind importance sampling.Journalof Econometrics,2009,149(1): 2–11.

[30]Durbin J,Koopman SJ.MonteCarlomaximum likelihood estimation fornon-Gaussian state spacemodels.Biometrika,1997 84(3): 669–684.

[31]Crainiceanu C,RubbertD,ClaeskensG,etal.Exact likelihood ratio tests forpenalised splines.Biometrika,2005,92(1):91–103.

[32]Jarrow R,Ruppert D,Yu Y.Estimating the interest rate term structure of corporate debtwith a semiparametric penalized spline model.Journalof the American Statistical Association,2004,99(465):57–66.

[33]RuppertD.Selecting thenumberof knots for penalized spline.Journalof Computationaland Graphical Statitics,2002,11(4):735–757.

[34]WahbaG.SplineModels forObservationalData.Pennsylvania:SIAM,Philadelphia,1990.

[35]Sima M D,Huffel S V.Regularized sem iparametric model identification with application to nuclearmagnetic resonance signal quantification with unknownmacromolecular base-line.Journalof the Royal Statistical Society:Series B,StatisticalMethodology, 2006,68(3):383–409.

[36]Shephard N,PittM.Likelihood anlysisofnon-Guassianmeasurement time series.Biometrika,1997,84(3):652–667.

[37]Ciprian M,Crainiceanua C M,Ruppert D.Likelihood ratio tests for goodness-of-fit of a nonlinear regression model.Journal of Multivariate Analysis,2004,91(1):35–52.

[38]Eraker B,JohannesM,Polson N G.The impactof jumps in returnsand volatility.Journalof Finance,2003,58(3):1269–1300.

[39]A¨ıt-Sahalia Y,Julio C D,Laeven R JA.Modeling financial contagion using mutually exciting jump processes.The Journal of Financial Econom ics,2015,117(3):585–606.

[40]A¨ıt-Sahalia Y,Kimmel R,Maximum likelihood estimation of stochastic volatility models.Journalof Financial Econom ics,2007, 83(2):413-452.

[41]A¨ıt-Sahalia Y,Jacod J.High-frequency Financial Econometrics.Princeton:Princeton University Press,2014.

HJM-based short ratemodelwith stochastic volatilities

Chen Zhiyong1,Jiang Liang2
(1.SchoolofManagement,Putian University,Putian 351100,China;
2.SchoolofMathematics,Putian University,Putian 351100,China)

This paper incorporates stochastic volatility and time–varying central tendency into the short-rate model(ECIR-SV)so that the Heath-Jarrow-Morton(HJM)modelnests the ECIR-SVmodel.This paperalso develops amaximum likelihood estimator for the ECIR-SV model by using the Laplace approximation and P-splinemethod based on importancesampling technique.Theempirical resultsshow that the ECIR-SVmodel is the best for the time series data comparison of the nested models.For the single-factormodelwith the time-varyingmean,themodel-fitting performancechangesslightly.Incorporating into the time-varying central tendency,the stochastic volatility model can better characterize the short rate dynam ics.Besides,the capital flowsstated by the time-varyingmean providesa reliable reference formacroeconom ic policy.

Heath-Jarrow-Mortonmodel;short rate;stochastic volatility;Laplace approximation;P-spline; long-run averagevalue

TP273

A

1000-5781(2016)02-0202-12

10.13383/j.cnki.jse.2016.02.006

2015-01-30;

2015-09-28.

国家自然科学基金资助项目(11471175);福建省科技计划项目软科学资助项目(2015R0070);莆田学院育苗基金资助项目(2014060;2014061);福建省自然科学基金资助项目(2016J01677).

陈志勇(1975—),男,福建莆田人,博士,副教授,研究方向:公共管理和公共政策,Email:czyla@163.com;

江良(1978—),男,福建莆田人,博士,副教授,研究方向:金融工程和金融计算,Email:ptjliang@163.com.