多维正相依再保险条约中最优自留向量的确定

张节松,肖庆宪(.上海理工大学管理学院,上海200093;2.淮北师范大学数学科学学院,安徽淮北235000)

多维正相依再保险条约中最优自留向量的确定

张节松1，2,肖庆宪1
(1.上海理工大学管理学院,上海200093;
2.淮北师范大学数学科学学院,安徽淮北235000)

为了探寻多维正相依风险在再保险业务中的最优自留额,应用条件极值理论,得到了依凸序最优自留向量满足的一般形式的方程组.在2维情形下,进一步应用单侧导数判断函数单调性,给出了最优解的显式表达式,并发现其可能取值的矩形域必为平面上的一个点.针对更高维情形,在自留损失方差最小与期望指数效用最大这两个特定准则下,假定索赔额分布属于对数正态分布族并依随机序正相依或者通过一个共同的指数分布正相依,分别给出了更易于求解的方程组.最后通过算例表明了所提方法的可行性与有效性.

相依风险;巨灾再保险;自留向量;效用;依随机序正相依

1　引　言

在保险精算理论中,索赔额相互独立是一个重要的假设,经典风险模型以及许多推广形式都建立在这一假定之上.然而,该假定与保险公司面临的风险环境存在较大差异,因为保险实务中的索赔风险往往是相依的.例如,由传染病所引起的医疗保险或生命保险、大雾天气中的汽车保险、汽车保险与第3方责任险以及位置相邻的房屋保险等.由于受共同因素或类似环境的影响,洪水、飓风以及地震等巨灾索赔风险则具有更为明显的正相依特征,这些相依风险往往会带来大额乃至巨额索赔,如一次输细管爆炸同时产生的企财险、车险、工程机械设备综合险以及意外伤亡险的索赔,累计可达几百万元甚至几千万元;一次地震的发生则可能引起高达十多亿元的各类赔付保险金.如果能充分考虑风险之间的相依关系,恰当地以再保险的方式分散风险,则不仅能减轻政府财政负担,减少经济损失,还能增加保险公司的业务量,提高承保能力[1].因此,正相依风险下,最优再保险策略以及相应参数的确定,具有重要的研究意义.

自留额的确定是再保险业务的核心之一,由于险种的多样化,每一险种又有其自身的特点,不同险种自留额的高低也有所不同［2］.如果再考虑到风险的相依性,这将是一项非常复杂的工作.文献[3]研究了索赔次数通过共同Poisson分布相依的双险种模型的最优超额赔款再保险,得到了最大化期望指数效用和调节系数下的最优自留额;文献[4]考虑了以相同方式相依的两风险模型的最优停止损失再保险,得到了VaR标准下的最优保留值及其存在条件;文献[5]进一步研究了动态环境中两相依风险模型的最优再保险问题;与文献[3–5]中索赔次数的相依关系有所不同,文献[6]研究了稀疏相关风险模型的最优超额赔款再保险,并在两个经济业务的假定下,给出了相应的最佳自留额.然而,上述模型中两种风险以及索赔额相互独立的假定与实际仍难以吻合.由于数学处理上的困难,讨论索赔额相依条件下更高维再保险问题的文献目前并不多见.其中,文献[7]在n维风险下(n≥2),以依随机序正相依(positively dependent through the stochastic ordering, PDS)的概念刻画索赔额的相依性,证明了超额赔款条约为一个统一优化准则下的最优再保险形式,并指出,因为相依风险的复杂性,要获得统一的n维风险模型中自留向量的显式表达式比较困难,于是就n=2的情形给出了方差最小与期望指数效用最大这两个准则下的最优自留额.

考虑到汽车保险、旅游保险、意外保险、健康保险以及财产保险等多维风险的存在性(实际上,如果进一步细分,一家保险公司经营的保险业务可达上百种),并注意到文献[7]中求2维自留向量的方法难以推广到n＞2的情形,本文应用条件极值理论,在严格验证前提条件的基础上,通过Lagrange乘子法,得到了n维自留向量所满足的n个方程,从理论上解决了文献[7]所述模型在一个统一优化准则下最优再保险条约中最优自留向量的一般性方程组表示问题,同时应用单侧导数判断函数单调性,改进了文献[7]关于2维风险下最优自留向量的结论.还在索赔额分布属于常见的对数正态分布族时,给出了依随机序正相依的一个简单判断条件,在方差最小的优化准则下,对n维自留向量所满足方程组给予了进一步推导,得到了更易于求解的表示形式.考虑到风险相依常常是由于受到共同因素的影响所致,又特别假定索赔额通过一个共同的指数分布相依(此时必然依随机序正相依),分别在方差最小与期望指数效用最大的优化准则下,对自留向量所满足的方程组进行了更为明确的表示,使之更便于获得显式解或应用智能算法搜索近似解,并给出了具体示例,应用粒子群优化算法,得到了自留向量的数值结果,以说明所提方法的可行性.

2　再保险模型

本文主要讨论文献[7]提出的n（＞2)维情形下超额赔款再保险条约中最优自留向量的确定问题,具体的模型表述见文献[7]的第1节和第2节,这里只做必要的分析介绍.

假定保险公司经营n种业务,由业务k产生的损失(索赔)为连续型随机变量Xk,k=1，2，...，n,总损失记为Sn=X1+X2+···+Xn.为了应对潜在的巨额损失,保险公司对业务k应用再保险策略lk,自留风险为lk（Xk）,再保险公司承担剩余损失,其中函数lk（x）在x≥0上递增且满足0≤lk（x）≤x,k= 1，2，...，n.于是,原保险公司自留总损失为

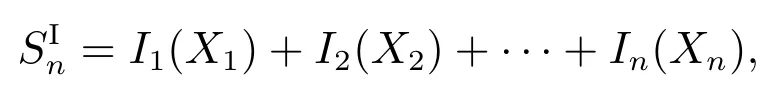
其中I=（l1，l2，...，ln）称为n维再保险条约.

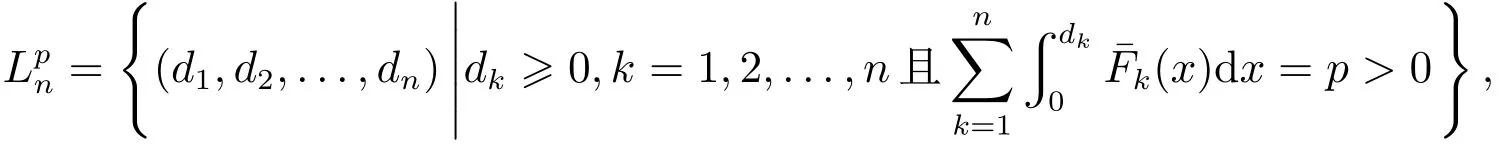
文献[7]使用一个统一的优化准则

其中u为凸函数,并在索赔向量（X1，X2，...，Xn）依随机序正相依时,证明了超额赔款再保险最优,即存在（d1，d2，...，dn）∈Rn,使得

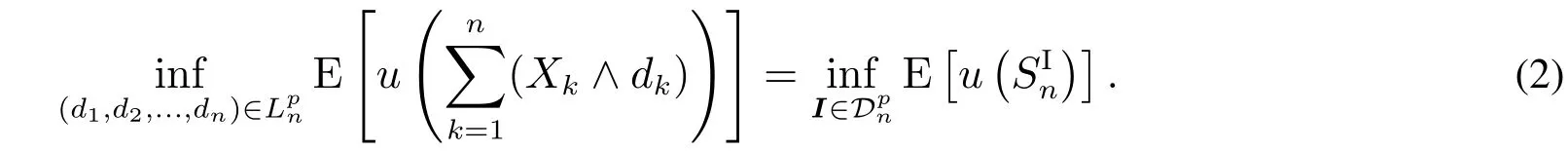
值得注意的是,依随机序正相依的概念对相依风险建模很有意义.实际上,在相依风险,尤其是巨灾风险中,损失的发生一般受到共同因素的影响,因此可视为同单调(comonotonic)的,另外,若已知任意k种经济业务的损失较大(1≤k≤n）,则任意一种经济业务损失较大的可能性也大,因此可视为条件递增(conditionally increasing,CI)的,而依随机序正相依包含了同单调及条件递增等情形.直观上说,如果某经济业务损失已知的条件下,其他经济业务损失大于任意给定值的可能性与已知值正相关,则风险是依随机序正相依的.关于依随机序正相依(PDS)的精确数学定义可参见文献[7–9]等.

不难发现,函数u（x）=x2,u（x）=eβx以及u（x）=-U（x）(β＞0,U（x）为凹效用函数)均为凸函数,可见优化准则(1)包含了自留损失的方差最小、期望指数效用最大以及凹期望效用最大等优化准则,所以式(2)意味着在这些准则下,超额赔款再保险条约都是最优的.

至此,一个自然的问题是超额赔款条约中的自留向量该如何确定.实际上,为了确保保险企业的财务稳定性及其偿付能力,许多国家将再保险的自留额列为国家管理保险业的重要内容[10].然而,文献[7]在确定最优再保险策略的同时,指出由于相依风险的复杂性,要获得多维相依风险下自留向量的表达式比较困难,并就两经济业务(即n=2)的情形,分别给出了方差最小与期望指数效用最大准则下自留向量的显式表达式.研究发现,2维风险下求自留向量的方法难以推广到n＞2的场合.这主要是因为,在n=2的情形下,自留向量形如（d1，d2）,而由期望保费原理知d2可看成d1的函数L（d1）,此时式(2)左边的目标函数退化为E［u（X1∧d1+X2∧L（d1））］,是d1的单变量函数.于是,文献[7]根据其右导数的正负号判断优化目标随d1变化而递增或递减的趋势,从而获得了最优解的显式表达式.显然,该方法在n＞2的情形下不再适用.考虑到已知最优策略为超额赔款条约,即那么寻求相应准则下的自留向量就相当于在此约束下求解的最小值点,从实际角度出发,又知最小值必然存在.此时,Lagrange乘子法是解决此类问题的有效方法之一,且不受变量维数的限制,同时,可将问题转化为由n个方程所构成的方程组的求解.进一步,在所得方程组难以获得显式解时,还可结合现代智能优化算法获得数值解.

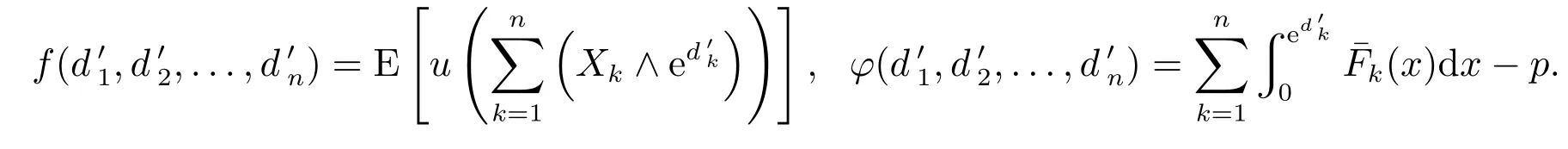
3　最优自留向量的确定

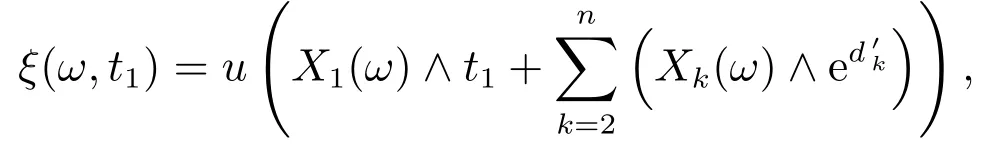
对任意固定的ω∈Ω,ξ（ω，t1）关于t1的右导数存在,且

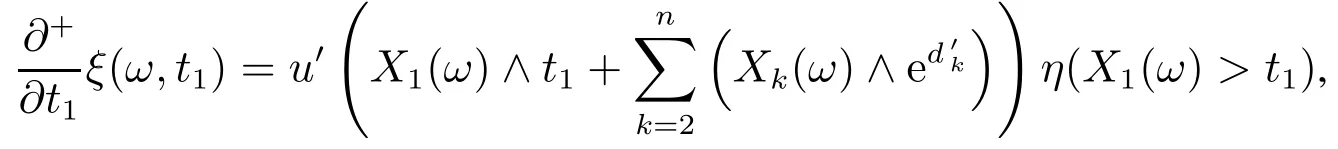
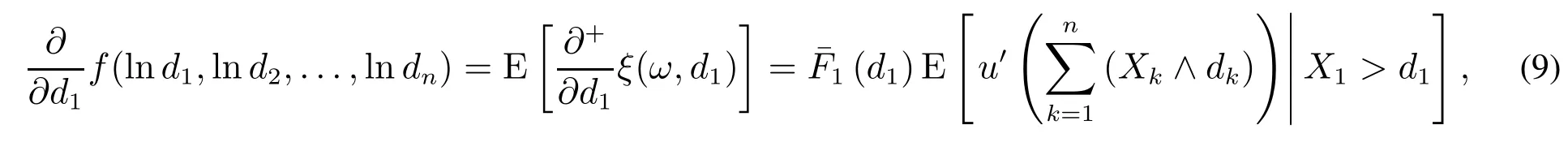
引理2函数φ有连续偏导数,

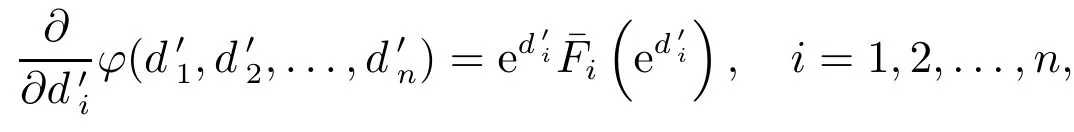
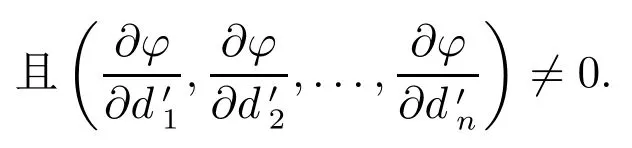
引理2是易见的,故略去其证明.

由引理1和引理2,用Lagrange乘子法,在约束条件的极小值,进而得到结论如下.

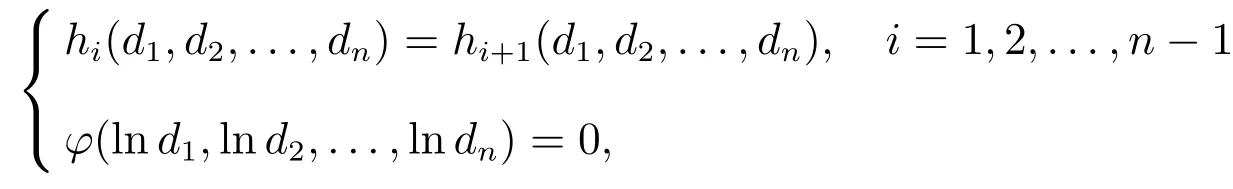
其中

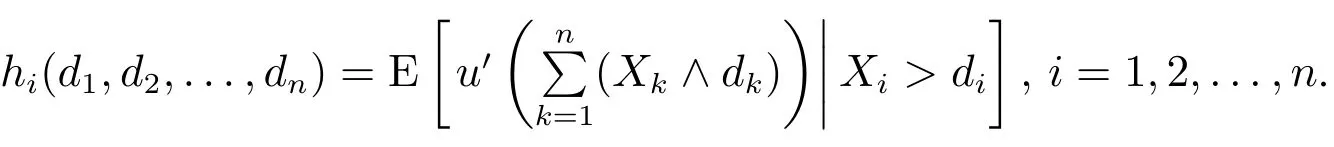
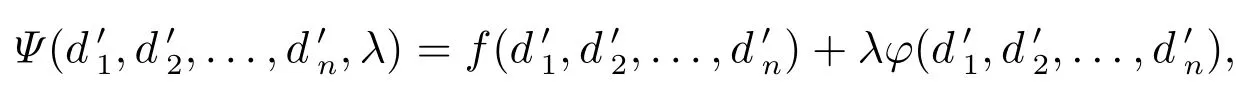
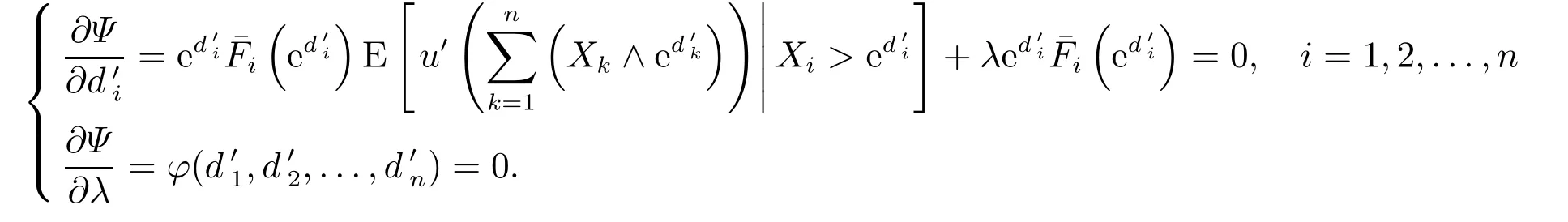
定理1的证明没有用到（X1，X2，...，Xn）依随机序正相依的条件.这表明无论各险种之间具有怎样的相依关系,就超额赔款再保险条约的最优自留向量而言,定理1总是成立的.如果Xk的分布已知,且各险种间的相依结构满足依随机序正相依的假定,根据文献[7],在优化准则(1)下,超额赔款再保险条约最优,而由定理1可得最优自留向量所满足的方程组.特别地,分别令u（x）=x2,eβx,-U（x）,其中β＞0，U＇＇（x）≤0,即可分别得到在保险公司自留总损失方差最小、期望指数效用最大以及期望凹效用最大的优化准则下,最优自留向量满足的一般形式的必要条件,这就从理论上解决了文献[7]所提出的多维正相依风险下自留向量的确定问题.后面的讨论将进一步表明,在给定索赔额的分布类型及相依结构时,方程组可进一步具体化并可求解,这在保险实务中是很有意义的.

文献[7]定理4.4和定理4.5分别给出了n=2时自留损失方差最小与期望指数效用最大准则下,最优自留向量的显式表达式,其中可能在一个矩形内取值.与那里的证明方法有所不同,下面结合引理1并应用单侧导数判断函数单调性,说明文献[7]所述的矩形实际上为平面上的一个点,并且该点与由定理1所得到的解是吻合的.

首先,当保险公司经营依随机序正相依的两业务并以稳定性作为优化目标(即方差达到最小)时,给出方差最小准则下唯一最优自留向量=的显式表达式.

命题1设（X1，X2）是PDS的,满足并对定义

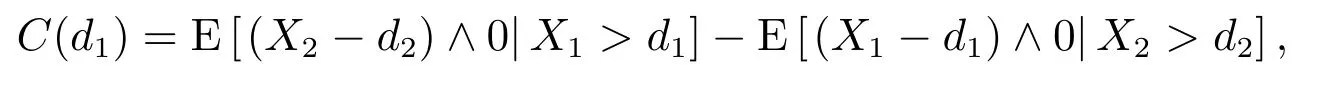
则C（d1）=0有且仅有一个实根且

证明由文献[7]的引理4.1知,L（d1）连续可微,结合式(4)取u（x）=x2，n=2的情形,得到

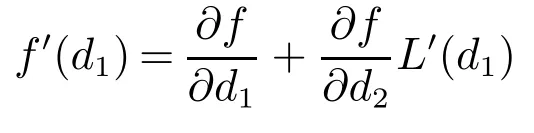
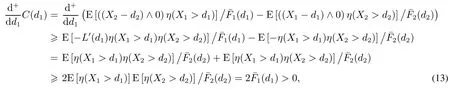
式(13)用到了文献[11]中定理2.4的(c).

因为C（d1）连续且右导数大于零,由文献[12]的定理1及其证明可知C（d1）关于d1严格递增,并且由

然而,不难发现B（d1）=C（d1）,可见在n=2时,命题1与定理1是相互吻合的.

当n=2时,在2维相依风险下,保险公司要在超额赔款再保险条约中实现效用最大化,即期望指数效用最大,由此得到唯一最优自留向量的显式表达式.有下列结论

命题2设（X1，X2）是PDS的,满足E［exp（β（X1+X2））］＜∞,其中β＞0,且（d1，d2）∈,记定义

则T（d1）=0有且仅有一个实根且

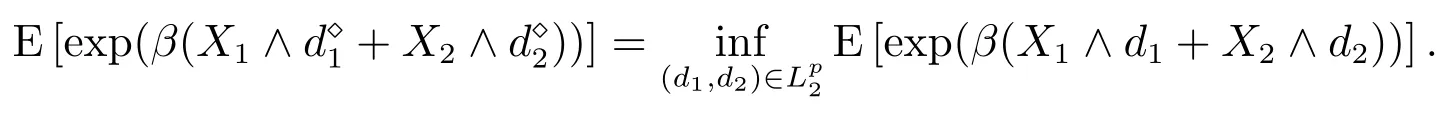
与文献[7]将优化问题转化为单变量函数优化问题,并通过右导数研究目标函数变化趋势的方法不同,本文采用的Lagrange乘子法不再受维数限制,从而获得了n＞2维情形下,自留向量所满足方程组的一般性表示,在包含文献[7]主要结果的同时,有了进一步拓展.另外,在2维情形下,本文采用单侧导数判断函数单调性从而获得的最优解(命题1,命题2)较文献[7]采用随机比较方法判断函数单调性(见文献[7]的式(4.6))从而获得的最优解(定理4.4,定理4.5),既相互吻合又有了明显的改进.当然,相依风险是复杂的, 在n＞2维情形下,由定理1一般仍难获得形如在n=2时给出的自留向量的显式表达式,必要时需结合适当的智能算法以获得数值解.

鉴于依随机序正相依结构一般不易直接判定以及定理1所述方程组可能存在求解上的困难,下面就两类具体的常见索赔分布类型、相依结构以及优化准则,给出依随机序正相依的判定方法,并对最优自留向量所满足的方程组给出更为具体的表示.

首先,假定索赔额分布属于保险精算中常见的对数正态分布族,给出依随机序正相依的一个简单判断条件,并在自留损失方差最小的优化准则下,对自留向量所满足的方程组予以具体表示.这有利于保险公司根据索赔数据分析相依结构,且更便于最优自留向量的确定.

命题3设Xi服从参数为μi和的对数正态分布,i=1，2，...，n,记（ln X1，ln X2，...，ln Xn）的协方差矩阵及其逆矩阵分别为如果对任意i/=j,αij≤ 0,则（X1，X2，...，Xn）是PDS的,若要自留损失的方差最小,则超额赔款再保险条约最优,并且自留向量满足方程组

证明记yi=ln Xi,则yi服从参数为μi和的正态分布,i=1，2，...，n,（y1，y2，...，yn）服从n维正态分布.因为∑-1满足αij≤0,若i/=j,由文献[13]知（y1，y2，...，yn）是MTP2(multivariate totally positive of order two)的,由文献[9]进一步知（y1，y2，...，yn）是PDS的.因为函数ex递增,于是又由文献[14]的命题2.13知（X1，X2，...，Xn）是PDS的.此时,根据文献[7],在自留损失方差最小的优化准则下,超额赔款再保险条约最优.

将式(18)代入方程组(17)即知方程组(16)成立.证毕.

其次,考虑到风险相依常因受共同随机源的影响所致,现假定某随机源服从指数分布,索赔额通过该指数变量相依,证明此时的索赔向量必然依随机序正相依,并分别在方差最小与期望指数效用最大的优化准则下,进一步明确自留向量所满足的方程组.这对保险公司为相依风险,特别是巨灾风险建立模型并在再保险条约中确定最佳自留额提供了一种思路及求解办法.

命题4设Z，Z1，Z2，...，Zn分别服从均值为1/θ，1/θ1，1/θ2，...，1/θn的指数分布且相互独立,其中θ，θk＞0,k=1，2，...，n.若Xk=Zk+Z,则（X1，X2，...，Xn）是PDS的.此时,若要自留损失的方差E最小,或者期望指数效用最大,β＞0,则超额赔款再保险条约均为最优策略,并且,

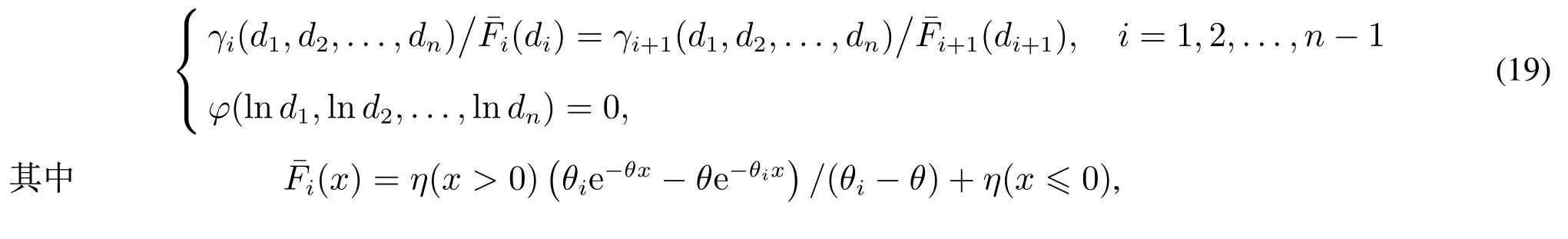
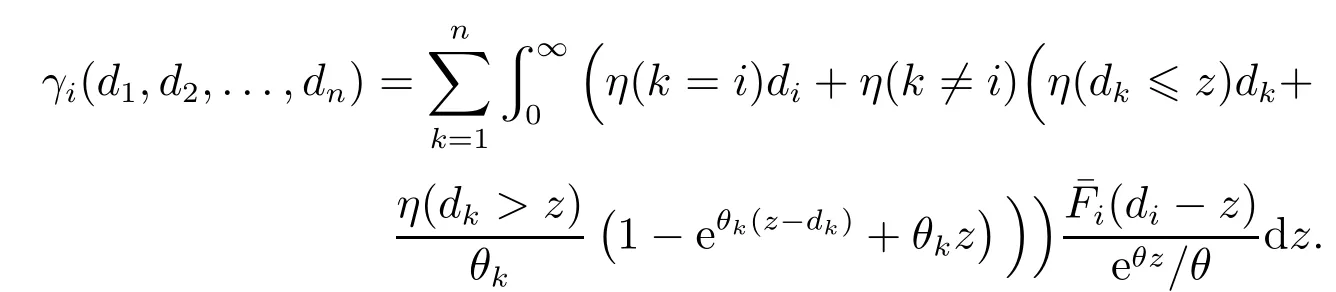
当θk=θ时,Xk服从Gamma分布,k=1，2，...，n.

证明设ζ服从均值为1/δ的指数分布,密度函数记为g（·）.由文献[15]知,对任意的δ＞0,g（·）为PF2 (P´olya frequency sequenceoforder2)函数.由此可见,n维随机向量（Z1，Z2，...，Zn）和（Z，Z，...，Z）的边际密度均为PF2的.由PDS的定义,易知（Z1，Z2，...，Zn）和（Z，Z，...，Z）分别是PDS的,且显然彼此独立,于是由文献[8]的定理5.2知（Z1+Z，Z2+Z，...，Zn+Z）,即（X1，X2，...，Xn）是PDS的.因此,根据文献[7],在自留损失的方差最小与期望指数效用最大的优化准则下,超额赔款再保险条约均为最优策略.

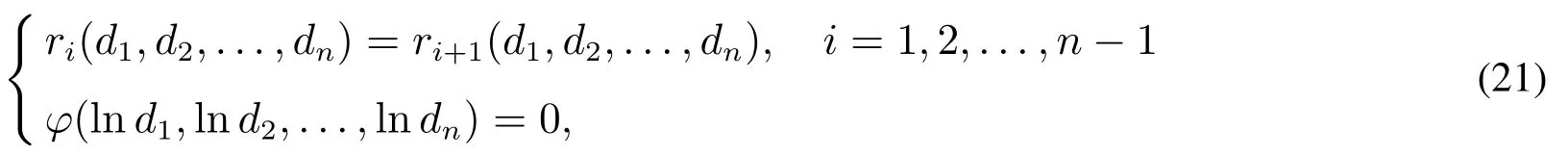
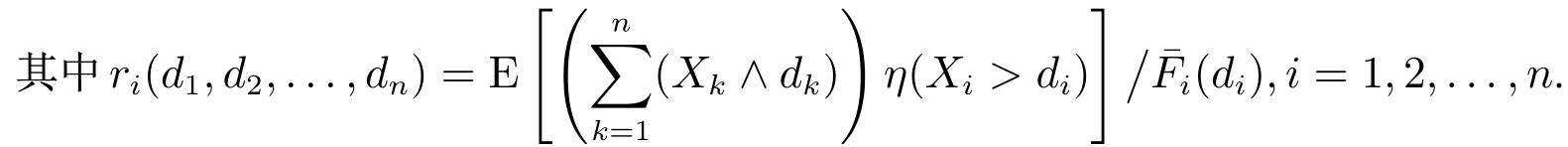
根据（Z，Z1，Z2，...，Zn）的独立性及连续型变量的全概率公式,有

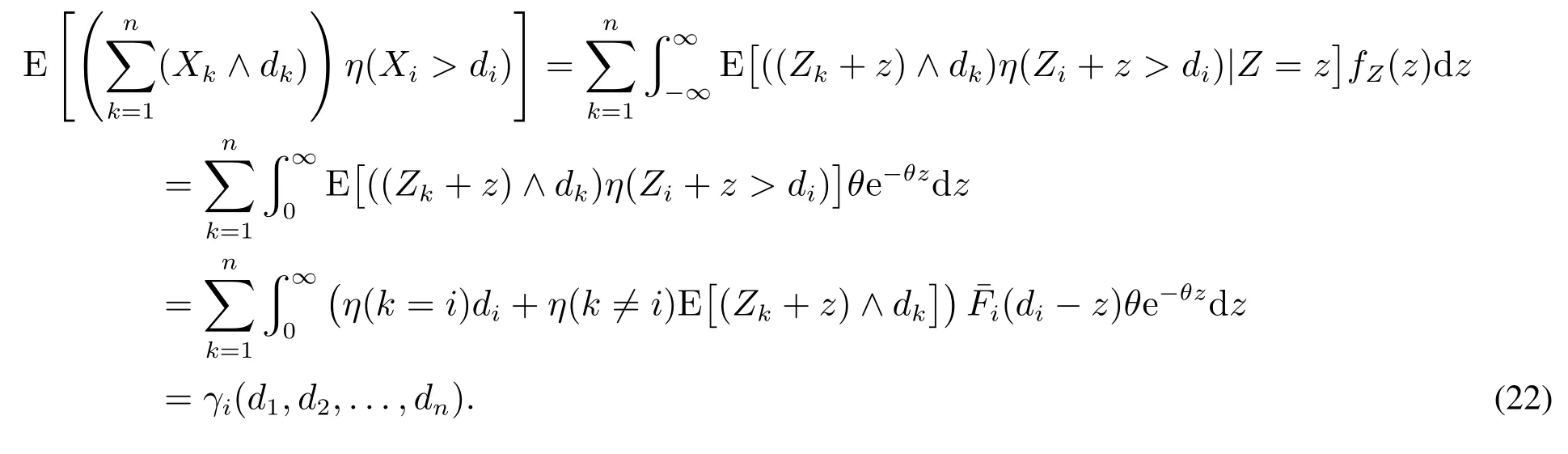
将式(22)代入方程组(21)即知1)成立.

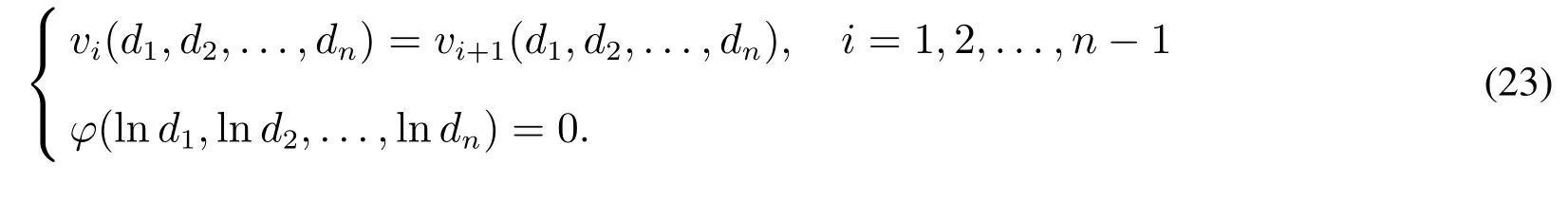
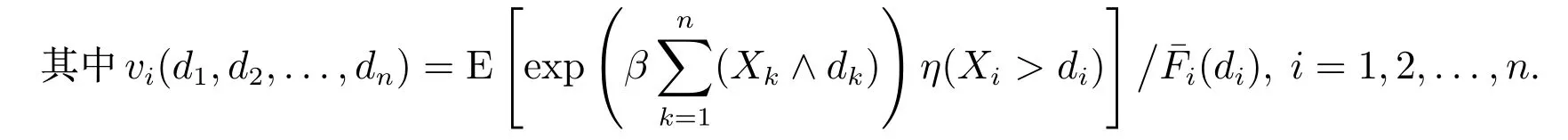
根据（Z，Z1，Z2，...，Zn）的独立性及连续型变量的全概率公式,有

将式(24)代入方程组(23)即知2)成立.证毕.

如果保险公司对n个依随机序正相依的保单分别再保险,上述结论仍然成立.

4　算例与分析

由命题1和命题2可知,在2维情形下,命题4的方程组(19)和方程组(20)的唯一解存在显式表达式,但对更高维的情形,一般很难得到.由此可以推知,定理1所给出的方程组并不总是存在显式解的,有时需要结合智能算法试求数值解.为说明数值解的可实现性,即更高维情形下利用定理1确定最优自留向量的可行性,本部分针对5维情形,就命题4进行示例,给出具体的数值结果.通过该示例,还可以观察到最优向量最小化方差与最大化指数效用的实际效果.

设保险公司经营5种经济业务,即在命题4中取n=5.以百万元为单位,设（Z，Z1，Z2，...，Z5）的均值向量为（4，2，5，6，8，10）,β=1/20.记（x1，x2，...，x5）=（86，112，131，172，213）,则对任意的k=1，2，...，5, Pr（Xk＞xk）≤10-9.据此并考虑到dk＞0的假定,给定dk,k=1，2，...，5的范围分别为

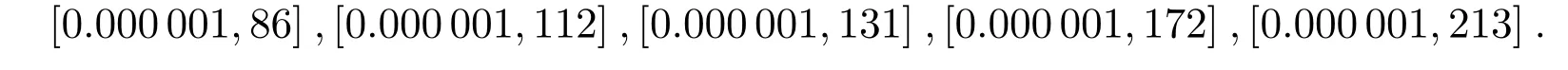
如果所有业务均实施全额再保险,且安全附加系数为0.15,需要的分保费为

假设原保险公司愿意支付的费用为30,即自留风险的期望值固定于

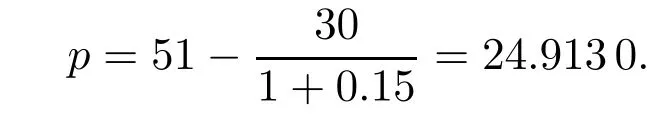
在上述给定参数下,观察对应的式(19)和式(20)发现,这两个方程组一方面可看成两个难以获得显式解的优化问题,可以借助智能算法搜索近似解,另一方面又都较为复杂,尤其是含有大量的积分运算,需要一种能快速迭代的算法加以实现.此时,若综合考虑寻优效果及寻优速度,粒子群智能优化算法是一种较好的选择,因为它容易实现、收敛快且精度较高,还可通过当前搜索到的最优值寻找全局最优解以防止局部最优情形的出现.因此,下面引入这一算法,其中适应函数选定为相应方程组中各个方程两边之差的绝对值之和.运用MATLAB R2012a,运行求解程序50次1为进一步防止局部最优点的出现,确保所得结果为最值点,这里选择较多次运行.,在总误差0.01下得到数值解

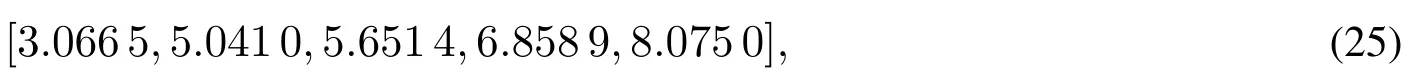
此时自留损失的方差为19.0436.同样运用MATLABR2012a,在总误差0.02下得到数值解

此时自留损失的期望指数效用为-3.5517.

类似地,在给定μi，σi及ρij,i，j=1，2，...，n的条件下,方程组(16)也可以通过粒子群算法获得数值解.

若将适应函数修改为相应方程组式(19)和式(20)中最后一个方程两边差的绝对值,即只要求满足保费原则,分别运行程序20次,所得结果对应的方差值均大于19.0436,有的达到199.6005;效用值均小于-3.5517,有的达到-4.9894,这进一步表明式(25)和式(26)均为最优解并且对于最小化方差和最大化效用具有显著的效果,在保障巨额损失的同时,有益于维护保险公司经营的稳定性与提高满意程度.

从式(25)和式(26)可以看出,d1，d2，...，d5的取值都比较适中,这与本示例中自留风险的固定值,或等价地,原保险公司愿意支付的分保费接近全额再保险所需费用一半的约定相一致,同时易见,对相对较大的风险,自留额也较大,这与自留风险函数递增的假定相吻合.

为了更直观形象地说明前述最优自留向量确定方法和结论、智能算法和数值结果的合理性,以及在最小化方差、最大化满意程度等方面的有效程度,最后,以2维情形为例,应用MATLAB软件分别绘制出期望保费原则下,自留损失的方差与效用随自留额变化的趋势图.

取ζ1，ζ2分别为上述示例中的X1，X2,即ζ1=Z1+Z,ζ2=Z2+Z,设自留风险的期望值固定于9.由此,先利用MATLAB软件绘制出条件函数φ（d1，d2）的3维图,记为G.记此条件下以自留向量为自变量的方差函数为g1（d1，d2）,利用MATLAB软件绘制出g1（d1，d2）的3维图G1.合并G和G1得如下图1.

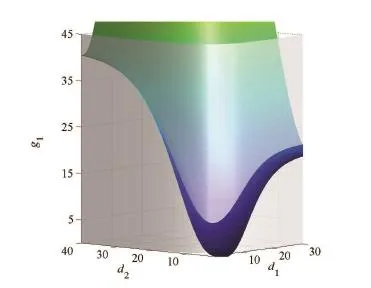
图1　2维PDS风险与期望值分保费下自留损失的方差Fig.1　Variance of retained lossunder two-dimensional PDS risksand expected reinsurance prem ium

类似地,记此时的期望指数效用为g2（d1，d2）,同样利用MATLAB软件绘制出g2（d1，d2）的3维图G2.合并G和G2得如下图2.

图1、图2中的竖直侧面均表示G,另外两个曲面分别为G1和G2,两条相交的空间曲线的高度则分别表示着方差和指数效用的大小.由G可见自留额d2(或d1)随着另一自留额d1(或d2)的增大而减少;由图1可见G与G1相交曲线的高度,即方差,沿着G随任一自留额di的增大先下降而后上升,并存在唯一最低点,i=1，2.记此时的自留向量为）,这就是方差最小准则下的最优自留向量;由图2可见,G与G2相交曲线高度,即指数效用,沿着G随任一自留额di的增大先上升而后下降,并存在唯一最高点,i=1，2.记此时的自留向量为,这就是指数效用最大准则下的最优自留向量.实际上,如果将方程组式(1 9)和式(20)退化到2维情形,同样应用粒子群算法,可得方差最小与效用最大准则下的最优自留向量分别为对应的方差和效用分别为6.4534和-1.5804.不难发现,图1、图2所显示的直观结果与命题1、命题2以及由本文提出的方程组表示并通过智能算法所实现的数值结果都是吻合的.另一方面,由图1还知,在满足保费原则下,最优自留向量能明显地最小化自留风险的方差,使原保险公司所面对的风险最为稳定;由图2还知,最优自留向量也能很好的最大化自留风险的期望指数效用,使保险公司在超额赔款再保险条约中获得最大的满意程度.

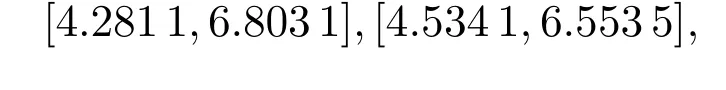
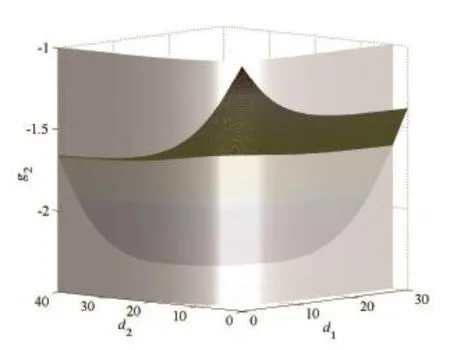
图2　2维PDS风险与期望值分保费下自留损失的效用Fig.2　Utility of retained lossunder two-dimensional PDS risksand expected reinsurance prem ium

5　结束语

保险实务中尤其是巨灾环境下,保险公司面临的风险往往是相依的,对承保标的大,风险波动也大的保险公司而言,相依风险往往还会带来巨额损失,有必要实施再保险.然而,由于相依风险的复杂性,再保险条约中的最优自留向量一般难以确定.本文在文献[7]提出的依随机序正相依风险下,应用相对极值理论,解决了超额赔款再保险这一最优再保险形式中自留向量所满足方程组的表示问题,同时应用单侧导数判断函数单调性,证明了2维情形下最优解的取值范围(矩形)为平面上的一个点,解决了最优解的唯一性问题.在索赔额分布属于常见的对数正态分布族时,文章给出了依随机序正相依的一个简单判断条件,同时考虑到相依风险的特征,在索赔额通过一个共同的指数分布相依时,对自留向量所满足的方程组给出了更为明确的表达式,使之更易于求解.研究表明,前述方程组在2维情形下的解具有显式表达式,对更高维的情形,文章通过具体示例并应用粒子群优化算法,得到了有效数值解.由此可见,本文所述方法是可行的,为保险公司在再保险条约中合理确定自留额,维护公司经营的稳定性,以及尽可能提高再保险业务的满意度提供了一种思路与方法.

[1]王丽珍,李秀芳.基于偿付能力的最优再保险策略.系统工程学报,2012,27(1):44–51. Wang L Z,Li X F.The optimal reinsurance strategy based onmaximal possible claims principle.Journal of Systems Engineering, 2012,27(1):44–51.(in Chinese)

[2]成显赫.谈谈再保险业务自留额的确定.保险研究,1999(7):35–36. Cheng X H.Discussion on the determ ination of retention of reinsurance.Insurance Studies,1999(7):35–36.(in Chinese)

[3]Centeno M L.Dependent risksand excessof loss reinsurance.Insurance:Mathematics and Econom ics,2005,37(2):229–238.

[4]朱亚茹.VaR下两相依风险的最优停止损失再保险.南开大学学报:自然科学版,2009,42(4):81–85. Zhu Y R.Optimal retention fora stop-loss reinsurance in dependent risksunder the VaR riskmeasure.Jounalof NankaiUniversity: NaturalScience,2009,42(4):81–85.(in Chinese)

[5]BaiL,CaiJ,ZhouM.Optimal reinsurancepolicies foran insurerwith abivariate reserve risk processin adynamic setting.Insurance: Mathematics and Econom ics,2013,53(3):664–670.

[6]胡凤清.稀疏相关风险模型的最优超额损失再保险.数学物理学报,2013,33A(2):317–326. Hu F Q.Optimal excess of loss reinsurance for a correlated risk modelwith thinning-dependence structure.Acta Mathematica Scientia,2013,33A(2):317–326.(in Chinese)

[7]Cai J,WeiW.Optimal reinsurancewith positively dependent risks.Insurance:Mathematics and Economics,2012,50(1):57–63.

[8]Block HW,Savits TH,Shaked M.A onceptofnegativedependenceusing stochastic ordering.Statistics&Probability Letters,1985, 3(2):81–86.

[9]Wang J.Bathtub FailureRatesofM ixtures in Reliability and the Simes Inequality underDependence in Multiple Testing.Pittsburgh: University of Pittsburgh,2008.

[10]魏华林,林宝清.保险学.北京:高等教育出版社,2012. WeiH L,Lin BQ.Insurance.Beijing:Higher Education Press,2012.(in Chinese)

[11]Joe H.MultivariateModelsand Dependence Concepts.London:Chapman&Hall/CRCPress,1997.

[12]M iller A D,V´yborn´y R.Some remarkson functionswith one-sided derivatives.The American MathematicalMonthly,1986,93(6): 471–475.

[13]Bhattacharya B.Covariance selection andmultivariate dependence.JournalofMultivariate Analysis,2012,106(C):212–228.

[14]Cai J,WeiW.On the invariantpropertiesofnotionsofpositivedependenceand copulasunder increasing transformations.Insurance: Mathematics and Econom ics,2012,50(1):43–49.

[15]Karlin S.TotalPositivity.Stanford:Stanford University Press,1968.

Determ ination of optimal retention vector inmulti-dimensional positively dependent reinsurance treaty

Zhang Jiesong1，2,Xiao Qingxian1
(1.Business School,University of Shanghai for Science and Technology,Shanghai200093,China;
2.SchoolofMathematical Sciences,HuaibeiNormalUniversity,Huaibei235000,China)

To explore the optimal retentions in reinsurance business with multi-dimensional,positively dependent risks,according to the theory of relative extreme value,a generalequations setwhich optim izes the retention vectorswith optimality through convex order isgiven.In the two-dimension case,by using one-sided derivative to judge themonotonicity of a function,the explicit expressions for the optimal solutions are obtained,and it is found that the rectangle region in which theymay locatemustbe ata pointon the plane.For the high-dimension case,equations easier to solve are given under two particular criteria ofminim izing the varianceormaximizing the expected exponentialutility of retained risks,assum ing that claim sizesare positively dependentthrough the stochastic orderingwhen the distributionsbelong to the fam ily of log normal,and that the claim sizes depending via a common exponential random variable,respectively.Finally,a numerical example is provided to illustrate the feasibility and validity of determ ining theoptimal retention vectorby the resulting equations.

dependentrisks;catastrophe reinsurance;retention vector;utility;PDS

F840,O211.9

A

1000-5781(2016)02-0214-13

10.13383/j.cnki.jse.2016.02.007

2014-10-23;

2015-12-24.

国家自然科学基金资助项目(11171221);安徽省高校优秀青年人才支持计划重点资助项目(gxyqZD2016104);安徽省高等学校自然科学研究资助项目(KJ2014B18).

张节松(1981—),男,安徽安庆人,博士生,研究方向:金融风险管理,保险数学,Email:j s zhang@126.com;

肖庆宪(1956—),男,河南信阳人,博士,教授,博士生导师,研究方向:金融工程,过程统计,Email:qxxiao@163.com.