两层分销链中的联盟定价策略与稳定性研究

李昌文,周永务(.华南理工大学工商管理学院,广东 广州5064;2.淮北师范大学数学科学学院,安徽淮北235000)

两层分销链中的联盟定价策略与稳定性研究

李昌文1，2,周永务1
(1.华南理工大学工商管理学院,广东 广州510641;
2.淮北师范大学数学科学学院,安徽淮北235000)

针对1个供应商和2个竞争零售商组成的分销供应链,研究了不同竞争强度下的联盟定价策略和稳定性.首先基于Stackelberg博弈模型给出了不同联盟结构下的定价策略;然后利用合作博弈理论中的Shapley值分配了联盟利润并探讨了大联盟的短视稳定性;最后运用最大一致集理论探讨了各种联盟结构的远视稳定性.结果表明,只有当竞争强度比较弱时,基于Shapley值分配利润的大联盟是短视稳定的;从远视的角度,供应链系统更可能出现的联盟结构为供应商–零售商联盟;当竞争激烈时,2个零售商的联盟也是远视稳定的.

供应链;合作博弈;Shapley值;稳定性;短视参与人;远视参与人

1　引　言

近年来,为了提高市场竞争力以及避免恶性竞争,企业纷纷寻求与其上下游甚至竞争对手相互合作,使得联盟成为当前商业活动的重要形式［1］.例如,1996年,湖北格力空调销售公司通过整合区域内所有经销商和零售商,实现统一定价,使其第二年销售量增幅高达40%;而供应链下游竞争零售商间的合作案例更是不胜枚举如家电连锁联盟“中水通泰”［2］.然而,每个企业作为独立的主体,其目标往往与联盟目标相互冲突,导致了?联盟的不稳定如重庆的“零利润?售肉联盟”［2］.因此,如何合理分配联盟利润使联盟具有稳定性,是当前学者和实践工作者?关注的热点问题之一.

已有文献主要利用合作博弈中的Nash谈判解和Shapley值方法来讨论供应链联盟利润的分配问题［3］.Nagarajan等［4］基于Nash谈判模型研究了组装供应链中组件供应商联盟的稳定性,公彦德等［5］在合作决策下运用不对称Nash谈判模型设计了供应链系统的利益分配方法.Robinson［6］是较早将Shapley值应用到供应链管理领域的学者,相关的后续研究文献有[7–10].对于利润分配后的联盟稳定性的判定,主要基于短视合作联盟与远视合作联盟［3］,现有研究集中于短视合作联盟的稳定性［7-12］,而针对远视合作联盟稳定性的研究刚刚兴起［13-17］.其中Nagarajan等［1］针对销售具有替代性产品的n个零售商,采用最大一致集(LCS)和联盟形成均衡过程(EPCF)讨论了远视零售商联盟结构的稳定性;Granot等［16］针对需求依赖于价格的组装供应链,在3种不同的博弈框架下讨论了上游组件供应商联盟结构的远视稳定性;Tian等［18］针对产品回收问题从远视角度考虑了制造商联盟的稳定性;郑士源等［19］针对航空联盟合作,从远视角度给出了稳定的航空联盟结构;郑士源［20］针对运输问题分析了联盟的远视稳定性;周水务等［2］针对需求依赖于价格的分销供应链,得到了竞争零售商联盟的短视和远视稳定结构.

综上所述,虽然以上文献应用远视概念讨论了联盟稳定性,但都仅仅针对单层零售商联盟或者单层组件供应商联盟进行讨论,几乎没有文献研究两层供应链中既有供应商又有零售商联盟合作的稳定性问题.基于此,本文针对一个包含单个供应商和2个竞争零售商的两层分销供应链,研究了供应链中参与人联盟合作后的利润分配以及相应的稳定性问题,这里不仅有零售商间的结盟,而且有供应商与零售商的结盟.

2　联盟合作模型构建与求解

2.1模型描述与假设

考虑完全信息下的一个2层分销供应链,其中包含1个风险中性的供应商S和2个风险中性的零售商R1，R2(这里称供应商和零售商为参与人).供应商S向2个零售商提供同一种产品,单位成本为c,零售商Ri向消费者提供产品的零售价格为pi，i=1，2.同文献[21,22]中的假设,零售商Ri的需求为

其中Ai＞0，θ＞0,Ai表示零售商Ri潜在的市场规模.θ反应了2个零售商之间的竞争强度,θ越大,竞争越激烈.

供应链系统内各个参与人之间可自由形成合作联盟Z⊆N.一种合作联盟结构是指对集合N的一种分割,即L=｛Z1，Z2，...，Zk｝,其中特别地,供应链内所有成员合作形成的联盟结构｛N｝称为大联盟(grand coalition).为方便,记供应商S为0,零售商R1，R2分别为1,2.则联盟结构有如下几种形式:3个参与人互不结盟｛0，1，2｝,任意2个参与人结盟｛（01），2｝,｛（02），1｝,｛0，（12）｝,以及大联盟｛（012）｝.本文假设供应商以及包含供应商的联盟都是Stackelberg博弈领导者.

2.2不同联盟结构下的定价决策模型

当3个参与人互不结盟时,供应商作为博弈领导者,首先决策其批发价格i=1，2;2个零售商作为跟随者,决策其零售价格i=1，2.用i=0，1，2表示参与人i的利润,此模型可以表示为

求解此问题,得到均衡解为

性质1当A2≥A1时,当A2≤A1时,

当供应商0和零售商1结成联盟｛01｝时,联盟｛01｝作为博弈领导者,首先决策其批发价格和自身零售价格零售商2作为跟随者决策其零售价格表示联盟｛01｝和零售商2的利润,此模型可以表示为

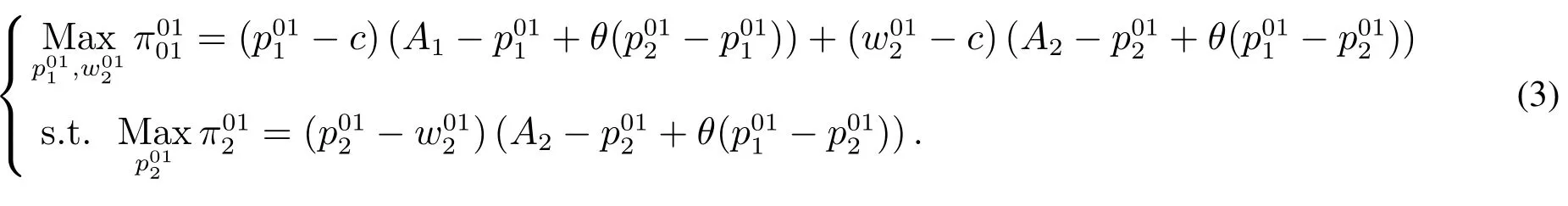
求解此问题,得到均衡解为

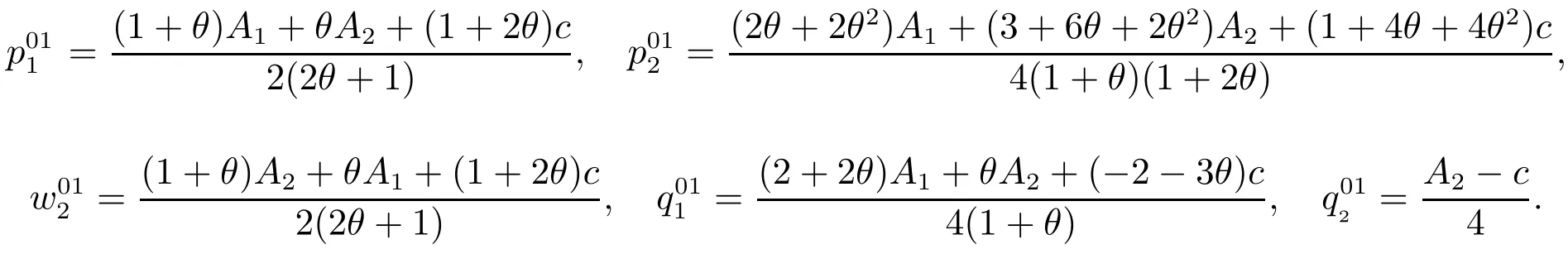
性质2当A2≥A1时,当A2≤A1时,

当供应商0和零售商2结成联盟｛02｝时,此时的求解与联盟结构｛（01），2｝类似.用分别表示其批发价格,零售价格和需求量;分别表示联盟｛02｝的利润,零售商1的利润和供应链系统总利润.

当零售商1和2结成联盟｛12｝时,供应商0作为博弈领导者,首先决策其批发价格ω12(当2个零售商结盟时,他们的批发价格相等),零售商联盟接着决策零售价格p12.用分别表示联盟｛12｝和供应商0的利润,此模型可以表示为

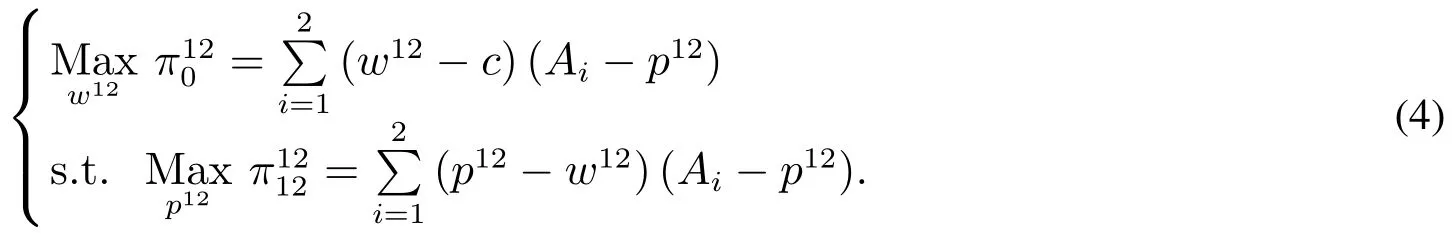
求解此问题,得到均衡解为

当供应商0和零售商1,2结成大联盟｛（012）｝时,三者共同决策其最优的零售价格p012,则大联盟的利润函数为

2.3对称零售商在不同联盟结构下的均衡结果

对于对称零售商,即当A1=A2=A时,在不同联盟结构下的均衡价格和需求量如表1所示,均衡利润如表2所示.

表1　对称零售商在不同联盟结构下的均衡价格和需求量Table1　Equilibrium pricesand demandsunder differentalliance structure for symmetric retailers

表2　对称零售商在不同联盟结构下的均衡利润Table 2　Equilibrium profitsunder differentalliance structure for symmetric retailers

由表1和表2可得到性质3.

性质3对称零售商在不同的联盟结构下,有如下关系成立:

性质3可以直接从表1和表2得到,该性质有如下意义:

1)当供应商或者包含供应商的联盟作为Stackelberg博弈领导者时,任何联盟结构内的批发价格都一样;

2)当供应商和某个零售商结盟时,联盟内零售商的零售价格最低;当2个零售商结盟时,零售价格最高,此时对消费者最不利;

3)当供应商和某个零售商结盟时,联盟内的零售商需求最大,而联盟外的零售商需求最小;

4)当零售商结盟时,供应链系统总利润最小,这是因为此时不但需求最小,同时上下游间又存在着双边际效应影响了供应链的绩效;当供应商和2个零售商结成大联盟时,此时不但没有零售商间横向的竞争,也没有了纵向间的竞争,供应链系统的总利润最高;当竞争强度比较弱时整个供应链在不联盟时的利润比供应商和单个零售商联盟时的要大,而当竞争强度比较大时正好相反.

3　联盟利润分配以及大联盟的短视稳定性

由于联盟稳定性讨论的复杂性,与文献[1,17,18]类似,这里只针对对称零售商进行分析.根据表2,利用最小最大方法［7］定义3人合作博弈（N，v）的特征值v（S）如下:

性质43人合作博弈（N，v）的特征值超可加.

根据特征值超可加的定义即可得出性质4,从而Shapley值分配满足个体理性.

下面给出合作博弈（N，v）核非空的条件.核非空是指合作博弈（N，v）存在一个分配φ=（φ0，φ1，φ2）满足如下条件:1)φi≥v（｛i｝），i∈N(个体理性);(有效性);(集体理性).若（N，v）存在非空的核,此时也称大联盟在相应的分配下短视稳定.

定理1合作博弈（N，v）核非空的充要条件是0＜θ≤1.

证明不妨假设φ=（φ0，φ1，φ2）是（N，v）的一个分配,根据零售商1和2的对称性有φ1=φ2,又根据有效性有φ0=v（｛012｝）-2φ1,从而核非空的分配φ=（φ0，φ1，φ2）应该满足如下不等式

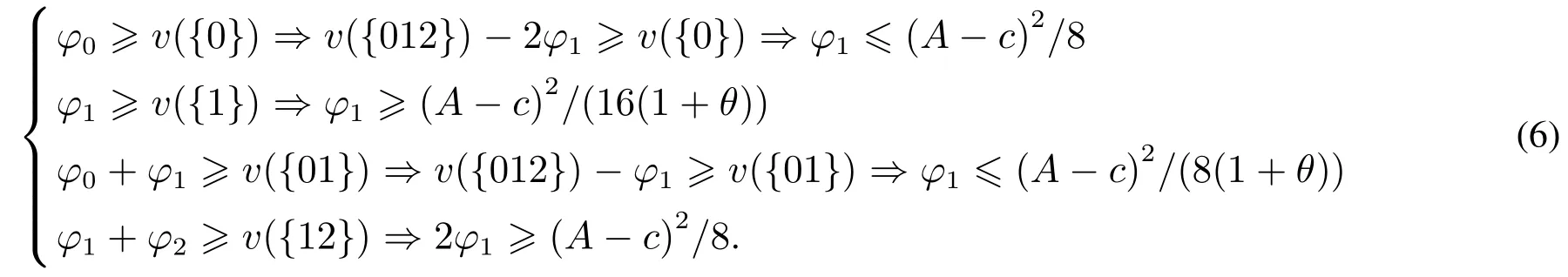
求解以上不等式,可以推导出核非空的充要条件是0＜θ≤1.

当核非空时,大联盟的分配方案有无穷多种,Shapley值分配是比较常用的一种分配方法.对于n人合作博弈（N，v）,参与人i的Shapley值中|S|表示S中的成员数目.根据上式可以计算出三人合作博弈的Shapley值分别为

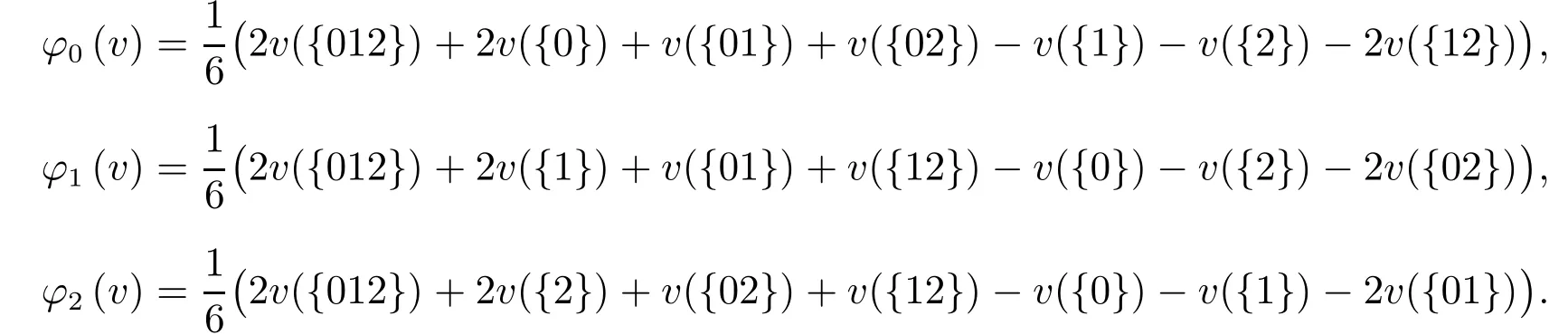
将3人合作博弈（N，v）的特征值分别代入上述式子中,相应的Shapley值分别为

定理2当0＜θ≤0.5时,合作博弈（N，v）的Shapley值在核中,基于Shapley分配利润的大联盟短视稳定,此时供应商给予零售商的转移价格为ω=φ0（v）/（A-c）+c.

证明因为Shapley值自身满足有效性,而根据性质4,其已满足个体理性,故只需其满足集体理性,即

求解上述不等式,可知当0＜θ≤0.5时,博弈（N，v）的Shapley值在核中,此时大联盟短视稳定.

对联盟结构｛（01），2｝,｛（02），1｝和｛（12），0｝中两人合作产生的利润,仍然采用Shapley值进行利润分配.则联盟结构｛（01），2｝中供应商0和零售商1的利润分别为

联盟结构｛（02），1｝中供应商0和零售商2的利润分别为

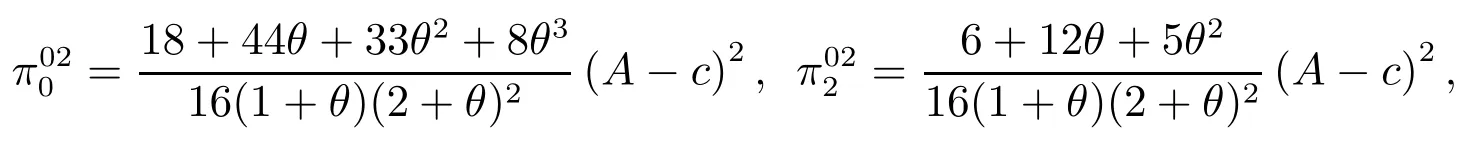
通过以上对不同联盟结构中的联盟利润进行分配,得到以下结论

性质51)当0＜θ≤0.618时,

4　远视联盟稳定性

目前关于联盟稳定性的讨论大多基于短视参与者,即仅考虑参与者的一步“叛逃”能否获得更高的利润,本文关于大联盟稳定性的讨论即属于短视稳定性.但是某个参与人发生一步“叛逃”之后有可能会引起其他参与人进一步的一系列“叛逃”,为了刻画这种多步“叛逃”下的结果,Chwe［13］提出了最大一致集(LCS)来刻画这种远视参与者联盟的稳定性.关于最大一致集以及与之相关的概念,见文献[2,13].下面使用最大一致集(LCS)给出联盟结构的远视稳定性.

定理3

证明1)当0＜θ≤0.618时,由性质5可知,供应商0的联盟偏好关系是

零售商1与2的联盟偏好关系是

首先,考虑当前联盟结构为大联盟L=｛（012）｝,则1个或2个参与人一步“叛逃”之后的联盟结构为V=｛（01），2｝,｛（02），1｝或者｛（12），0｝.但是显然LB;

(b)如果V=｛（02），1｝,则与V=｛（01），2｝类似;

(c)如果V=｛（12），0｝,则S=｛1，2｝或者S=｛0｝,考虑如下“叛逃”过程

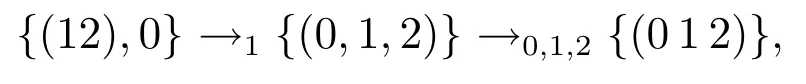
由于｛（12），0｝≺1｛（0 12）｝并且｛0，1，2｝≺0，1，2｛（0 12）｝,如果记B=｛（012）｝,则有

综合以上,根据最大一致集的定义有｛（012）｝∈LCS.

下面考虑联盟结构为L=｛（01），2｝,则参与人一步“叛逃”之后的联盟结构为

(a)如果V=｛0，1，2｝,则S=｛1｝或者S=｛0｝,考虑“叛逃”过程

由于｛（0，1，2｝≺0，1｛（01），2｝,如果记B=｛（012）｝,则有V≪B,但是L/B;

(b)如果V=｛（02），1｝,则S=｛02｝,令B=｛（02），1｝,则有V=B,但是LB;

(c)如果V=｛（12），0｝,则S=｛12｝,令B=｛（12），0｝,则有V=B,但是LB;

(d)如果V=｛（012）｝,则S=｛012｝,令B=｛（012）｝,则有V=B,但是LB.

综合以上,根据最大一致集的定义有｛（01），2｝∈LCS.

对于联盟结构为L=｛（02），1｝,由于零售商1与2对称,从而也有｛（02），1｝∈LCS.

最后,假定当前联盟结构为L=｛0，1，2｝或｛0，（12）｝,如果一步“叛逃”之后的联盟结构为V=｛（012）｝,其中S=｛0，1，2｝,则不能找到联盟结构B满足V=B或V≪B使得LB,因此｛0，1，2｝,｛0，（12）｝/∈LCS.

采用类似的方法可以证明2)～4)成立.证毕.

由定理3可知,基于Shapley值分配利润的大联盟在0＜θ≤0.618内远视稳定,在0.5＜θ≤0.618内不是短视稳定的,即联盟内的短视参与人可能会发生一步叛逃.但是远视参与人会考虑自身的一步叛逃会引起其他参与人的一系列叛逃,最终来看,大联盟仍然是最初叛逃参与人的最好选择,即大联盟远视稳定.然而当竞争强度比较大时(θ＞0.618）,大联盟无论从短视还是远视角度都不稳定,这也符合实际中虽然有类似于格力空调销售股份公司这样的大联盟,但是能够成功的案例并不多见.从远视角度,更可能发生的联盟是供应商-零售商联盟,这与现实中所出现的大多数零-供联盟相吻合,如海尔与苏宁结成的战略联盟,宏图三胞与联想结成的战略联盟等.当市场竞争充分激烈时(θ＞1.281）,还有可能发生2个竞争零售商的联盟,如引言中提及的家电连锁联盟“中水通泰”.

5　结束语

基于合作博弈的视角,本文研究了单供应商两竞争零售商联盟合作定价策略以及稳定性.在供应商和零售商可以自由结盟的假设下,对不同的联盟合作形式采用Shapley值分配了联盟利润并讨论了其稳定性.结果表明,无论竞争强度是多少,大联盟结构下供应链系统的利润最高.但是,当竞争强度比较激烈时,Shapley值分配规则并不能使得各方都满意,供应链系统中更可能发生供应商和其中某一个零售商合作.本文考虑的是供应商–Stackelberg并且零售商对称情形下的联盟稳定性问题,进一步的可以研究零售商–Stackelberg以及使用其他联盟利润分配方法下的联盟稳定性,以及从有盟主联盟与无盟主联盟和有无股权参与方面进行讨论.

[1]Nagarajan M,Sosic G.Stable farsighted coalitions in competitivemarkets.ManagementScience,2007,53(1):29–45.

[2]周水务,肖旦,汤勤深,等.分销供应链中竞争零售商联盟的稳定性.运筹与管理,2013,22(4):50–59. Zhou YW,Xiao D,Tang QS,etal.Stability of coalitionswith competitive retailers in distribution supply chains.Operation Research and ManagementScience,2013,22(4):50–59.(in Chinese)

[3]NagarajanM,SosicG.Game-theoretic analysisof cooperation among supply chain agents:Review and extensions.European Journal ofOperationalResearch,2008,187(3):719–745.

[4]Nagarajan M,Bassok Y.A bargaining framework in supply chains:The assembly problem.Management Science,2008,54(8): 1482–1496.

[5]公彦德,李帮义,刘涛.基于物流费用分摊比例的闭环供应链模型.系统工程学报,2011,26(1):39–49. Gong Y D,Li B Y,Liu T.Model for closed–loop supply chain based on the loading ratio oflogistics cost.Journal of Sytems Engineering,2011,26(1):39–49.(in Chinese)

[6]Robinson LW.A commenton Gerchak and Gupta’s“On apportioning costs to customers in centralized continuous review inventory systems”.JournalofOperationsManagement,1993,11(1):99–102.

[7]LengM,ParlarM.Transferpricing in amultidivisional firm:A cooperativegameanalysis.OperationsResearch Letters,2012,40(5): 364–369.

[8]Meca A,Timmer J,Garc´ıa-Jurado I,etal.Inventory games.European JournalofOperationalResearch,2004,156(1):127–139.

[9]Guo H,Leng M,Wang Y.Interchange fee rate,merchantdiscount rate,and retail price in a credit card network:A game-theoretic analysis.NavalResearch Logistics,2012,59(7):525–551.

[10]Bernstein F,Kok A G,Meca A.Cooperation in assembly systems:The role of know ledge sharing networks.European Journal of OperationalResearch,2015,240(1):160–171.

[11]Meca A.A core-allocation fam ily forgeneralized holding costgames.MathematicalMethodsof OperationsResearch,2007,65(3): 499–517.

[12]Guardiola L A,Meca A,Puerto J.Production-inventory games:A new class of totally balanced combinatorialoptim ization games. Gamesand Econom ic Behavior,2009,65(1):205–219.

[13]ChweM.Farsighted coalitionalstability.Journalof Economic Theory,1994,63(2):299–325.

[14]Nagarajan M,Sosic G.Coalition stability in assemblymodels.OperationsResearch,2009,57(1):131–145.

[15]Sosic G.Impactof demand uncertainty on stability of supplier alliances in assemblymodels.Production and OperationsManagement,2011,20(6):905–920.

[16]GranotD,Yin S.Competition and cooperation in decentralized push and pullassembly systems.ManagementScience,2008,54(4): 733–747.

[17]Nagarajan M,Sosic G,Zhang H.Stable Group Purchasing Organizations.Los Angeles:Marshall School of Business,No.FBE, 2012.

[18]Tian F,Sosic G,Debo LG.Green Recycling Networks.LosAngeles:MarshallSchooleof Business,University of Southern California,2013.

[19]郑士源,王浣尘.基于动态合作博弈理论的航空联盟稳定性.系统工程理论与实践,2009,29(4):184–192. Zheng SY,Wang HC.Airlinealliancestability based on dynam ic cooperativegame theory.SystmesEngineering:Theory&Practice, 2009,29(4):184–192.(in Chinese)

[20]郑士源.基于动态稳定性的运输联盟成本分摊规则.上海交通大学学报,2013,47(3):500–504. Zheng SY.Costallocation schemes for transportation alliance based on farsighted stability.Journalof ShanghaiJiaotong University, 2013,47(3):500–504.(in Chinese)

[21]M cGuire TW,Staelin R.An industry equilibrium analysisof downstream vertical integration.Marketing Science,1983,2(2):161–191.

[22]Chen RR,Roma P.Group buying of competing retailers.Production and OperationsManagement,2011,20(2):181–197.

Study on thealliance pricing strategy and stability of a two-echelon distribution supp ly chain

LiChangwen1，2,Zhou Yongwu1
(1.Schoolof Business Adm inistration,South China University of Technology,Guangzhou 510641,China;
2.SchoolofMathematical Science,HuaibeiNormalUniversity,Huaibei235000,China)

For a two-echelon distribution supply chain composed of a single supplier and two competing retailers,thealliance’spricing strategy and stability are studied underdifferentcompetitive intensities.Firstly, this paper analyzes the differentalliance pricing strategies based on Stackelberg games;then it allocates the alliance profits based on Shapley value and considers themyopic stability of the grand coalition;finally,it discusses the farsighted stability of all the coalition structures.The result shows that the grand coalition is myopically stableonlywhen the competitive intensity is relativelyweak,and that the supplier-retaileralliance ismore likely to happen in the long run.With intense competition,the two-retailer alliance is also farsighted stability.

supply chain;cooperativegame;Shapley value;stability;myopic players;farsighted players

F224.3

A

1000-5781(2016)02-0234-09

10.13383/j.cnki.jse.2016.02.009

2014-05-25;

2015-04-20.

国家自然科学基金资助项目(71131003;7137075;71402171;71201044;11501233;71501077);教育部人文社科基金资助项目(13YJC630075;15YJC630053);广东省自然科学基金资助项目(2014A030310212;2014A030310443);安徽省高等学校自然科学研究重点资助项目(KJ2015A335;1508085SMA204).

李昌文(1979—),男,安徽潜山人,博士生,讲师,研究方向:供应链联盟运作优化,Email:cw li2008@163.com;

周水务(1964—),男,安徽庐江人,博士,教授,博士生导师,研究方向:物流与供应链管理,Email:zyw666@hotmail.com.