随机偏好下的Borda悖论

吴　凡,赵　勇,陈煌琼(.华中科技大学系统工程研究所,湖北武汉40074;2.江苏省邮电规划设计院有限责任公司,江苏南京2009;.国家知识产权局专利局专利审查协作江苏中心,江苏苏州256)

随机偏好下的Borda悖论

吴凡1，2,赵勇1,陈煌琼3
(1.华中科技大学系统工程研究所,湖北武汉430074;
2.江苏省邮电规划设计院有限责任公司,江苏南京210019;
3.国家知识产权局专利局专利审查协作江苏中心,江苏苏州215163)

在阐明二元随机偏好所存在缺陷的基础上,提出了一种更具普适性的随机偏好表示方法——概率分布型随机偏好,并论证了这种表示方法的完备性(即该方法可以表示所有可取的随机偏好).然后基于概率分布型随机偏好, 将Borda悖论涉及的两种投票规则推广为随机情况,分析随机偏好下Borda悖论的发生规律,并进一步从权值向量和投票人数两方面比较所得结论与确定性偏好下Borda悖论的异同,分析出现差异的原因.

Borda悖论;随机偏好;概率分布;随机投票规则

1　引　言

投票悖论是社会选择领域一类反常现象的统称,它的出现往往加剧了个体理性和集体理性之间的冲突,使个体偏好在既定规则下无法集结成理性的社会偏好,最终导致选民对社会选择活动公平性和合理性的质疑.事实上,投票悖论甚至不需要真正出现,即使其潜在的可能性也会阻碍活动的进行.Borda悖论是投票悖论中具有代表性的一种,曾多次在实际活动中出现,给多种常见社会选择规则(如简单多数票)的合理性带来了巨大的挑战［1］.

常见的Borda悖论有弱Borda悖论,强Borda悖论和严格Borda悖论.本文的研究对象是强Borda悖论,这种悖论最早由Borda［2］借助一种21个投票人的偏好断面进行例证,因具有较大的实际研究价值得到了学者们的广泛关注［1］.捉对投票失败者(pairw isemajority rule loser,PMRL)在既定投票规则中获胜的现象称为强Borda悖论.这种既定规则的范围几乎没有限制,可以是除捉对投票规则(pairw isemajority rule,PMR)外的任意规则,目前研究最深入的是排位投票制规则(positional voting rules,PVR).一般情况下,PMR规定候选人两两捉对比较,所有捉对比较均获胜的候选人当选;当候选人之间出现Condorcet循环时,通过计算Condorcet社会选择函数的函数值大小对候选人进行排序.PVR规定将权值向量中的各权值依次赋予个体偏好中相应位次的候选人,计算各候选人所获得的权值总和并按权值总和对候选人进行排序.PVR是一类投票规则的总称,以权值向量的不同加以区分.本文在无歧义的情况下将强Borda悖论简称为Borda悖论.

目前对Borda悖论的研究基本上都是以确定性偏好为前提.G¨ardenfors［3］和Fishburn等［4］已经证明,除线性权值向量外,所有非线性权值向量的PVR都有可能出现Borda悖论,且悖论的发生概率与选民人数和权值向量相关.Gehrlein等［5］和Diss等［6］给出了不同文化条件下这种相关性的函数表达式,在此基础上研究了投票人数趋近于无穷大时悖论发生概率的极限,并进一步分析了概率值与个体偏好互相关性之间的关系.然而,随着社会选择理论的不断发展,越来越多的学者意识到确定性偏好的局限［7，8］,这种局限性在重复性决策时尤为明显.Tversky［9］指出,如果需要对两个备选项进行重复性选择,决策者通常会在某些特定情况下选择其中一个而在其他情况下选择另一个,也就是说个体偏好在整个决策过程中并不一定会保持一致,随机偏好可以准确地表达这种情况下的不一致性.

本文针对重复性决策问题讨论随机偏好下的Borda悖论发生规律.考虑到现有的随机偏好表示方法［10-12］在PVR等多种投票规则中应用时存在着不能准确表达个体偏好的缺陷,本文首先提出一种新的更具普适性的随机偏好表示方法,在此基础上将PVR扩展为随机投票规则,进一步研究随机偏好下Borda悖论的发生规律,并将这种发生规律与确定性情况从权值向量和投票人数两方面进行对比,分析两种情况下Borda悖论发生规律异同的内在原因.

2　随机偏好表示方法的一种改进

现实生活中的社会选择通常采取或可归结为投票的方式进行,可以引入下列符号进行统一化描述.

设群由m个投票人和n个候选人构成,简记为〈m，n〉群,用V=｛v1，v2，...，vm｝表示群中投票人的集合,C=｛c1，c2，...，cn｝表示候选人的集合.投票人vi的偏好记为pvi,｛pv1，pv2，...，pvm｝表示所有个体偏好确定后所形成的偏好断面.pG=g（pv1，pv2，...，pvm）表示通过社会选择规则g将个体偏好集结成群偏好pG.

为了限定本文投票模型的范围,给出下列基本假设:

假设1投票人相互独立地表达自身偏好;

假设2候选人之间具有连通性.

需要指出的是,假设2中的连通性已经推广为随机情况,即∀ci，cj∈C,必然∃π∈［0，1］,使得ci≻cj的概率为π.当π∈［0，1］退化为π∈｛0，0.5，1｝时,随机情况下的连通性随即转变成确定性情况.

2.1二元随机偏好的不足

目前,对随机偏好的研究大部分定义在“严格优于”这种二元关系上,本文将其称为二元随机偏好(stochastic preference based on strictorder,SPSO),如定义1[12]所示.

定义1设cx，cy∈C,vi∈V,πG（cx≻cy），πvi（cx≻cy）∈［0，1］分别表示群和投票人vi认为候选人cx和cy间关系为cx≻cy的概率.

1)若πG（cx≻cy）≥0.5，πvi（cx≻cy）≥0.5,分别称群和投票人vi认为cx随机不劣于cy;

2)若πG（cx≻cy）＞0.5，πvi（cx≻cy）＞0.5,分别称群和投票人vi认为cx随机优于cy;

3)若πG（cx≻cy）=0.5，πvi（cx≻cy）=0.5,分别称群和投票人vi认为cx随机无差异于cy.

由定义1可知,当πG（cx≻cy），πvi（cx≻cy）=0或1时,偏好的随机性将会消失,随机偏好退化为确定性偏好.以SPSO为基础,参考文献[11,13]等中随机偏好在实际应用中的需要,可以进一步定义个体偏好和群偏好.

定义2设C=｛c1，c2，...，cn｝为候选人的集合,则概率框架下的个体偏好和群偏好都可以表示为

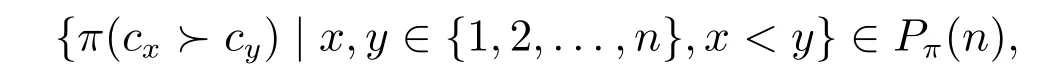
其中偏好分量π（cx≻cy）表示候选人cx和cy间关系为cx≻cy的概率,Pπ（n）称为随机偏好空间,即随机偏好的取值范围,具体可以表示为

SPSO因为表达形式简单得到了广泛的应用,然而这种表示方法在PVR等规则中使用时具有较大的局限性,下面举例说明.

例1考虑同样含有100个投票人和3个候选人c1、c2和c3的3个群:A群、B群和C群,投票人在3个群中的偏好分布如表1所示.现在从每个群中随机抽取20个投票人进行投票,通过给定的投票规则(PMR和PR)将这些个体偏好集结成最终的群偏好.

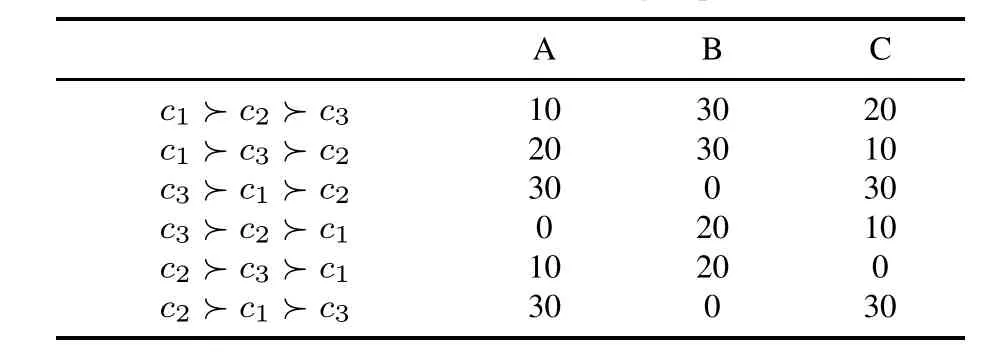
表1　投票人偏好分布情况Table1　Preference distributions of group A,B and C

由表1可知,A、B和C群中偏好c1≻c2≻c3被抽中的概率分别为0.1、0.3和0.2,同理可以求出其他5种偏好被抽中的概率.进一步分析可知,3个群中偏好c1≻c2,c1≻c3和c2≻c3被抽中的概率均分别为0.6,0.6和0.5.因此,在不知道被抽出投票人具体偏好的情况下,个体偏好都可以预估为

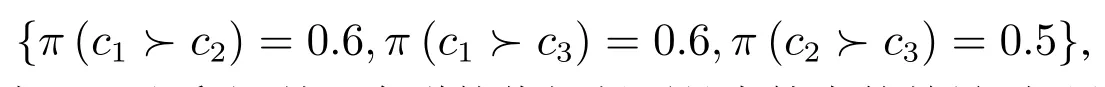
这是SPSO的表达形式.由表1可以看出,这3个群的偏好断面具有较大的差异.如果投票规则为PMR,由于SPSO完全相同,3个群的群偏好预估应该完全一致;如果投票规则为PR,显然A群中候选人c2被抽中的概率最大,为0.4,相应地c2获胜的概率也最大,同理可知B群中c1获胜的概率最大,C群中c3获胜的概率最大.相同的投票规则在相同的个体偏好下可能会得出3个截然不同的群偏好!

其实除了PR外,例1显示出的问题也可能会在其他权值向量下的PVR中出现.由于SPSO表示方法在PVR中使用时可能无法准确表达投票人的个体偏好,使得群偏好的规范化求解变得困难.因此,讨论随机偏好下的Borda悖论不能采用SPSO表示方法.

2.2概率分布型随机偏好

例1在揭示SPSO局限性的同时,也从侧面给出了对其改进的方法.以A群为例,可以将随机抽取的个体偏好预估为

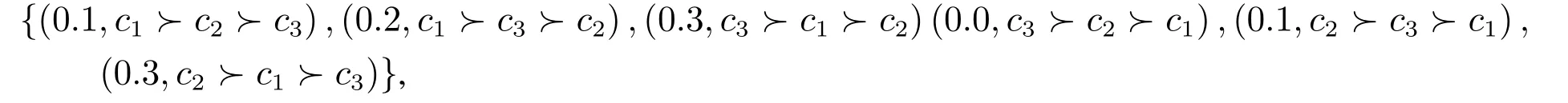
这种表示方法相对于SPSO可以更细致准确地表达个体偏好,避免了例1中提出的问题.下面在阐述这种随机偏好表示方法理论依据的基础上给出定义,并探讨这种表示方法是否可以表示随机偏好空间中所有可能的偏好.

首先给出折中偏好、凸偏好集和极端偏好的概念,这是定义新的随机偏好表示方法的基础.

定义3设p1，p2，...，pn是任意n个偏好,权值ω1，ω2，...，ωn∈R+满足约束条件,则称为这n个偏好的折中偏好,记为pmid（p1，p2，...，pn）.

定义3中的n个偏好可以全部是确定性偏好或随机偏好,也可以是确定性偏好和随机偏好的混合. 当n=1时,折中偏好退化为单个偏好.

定义4设偏好集S/=Ø,若∀p1，p2∈S,｛pmid（p1，p2）｝⊆S成立,则称S为凸偏好集.

由定义4可知,∀n≥2,随机偏好空间Pπ（n）都是凸偏好集.

定义5设凸偏好集S（|S|＞1）内有一偏好p,若∀p1，p2∈S且p1/=p2,p/=pmid（p1，p2）,则称p为S中的极端偏好.

当|S|=1时,由定义4可知S一定是凸偏好集,然而此时不存在极端偏好的概念,因此在定义极端偏好时应去除这种情况.为便于理解极端偏好的概念,举例说明如下:

在凸偏好集P=｛π（c1≻c2）|π（c1≻c2）∈［0，1］｝中,π（c1≻c2）=0不能表示为P中任意两个不同偏好的折中偏好,因此π（c1≻c2）=0为P中的一个极端偏好.

由于Pπ（n）是凸偏好集,因此可以在Pπ（n）中进一步讨论极端偏好的概念.定理1给出了Pπ（n）中极端偏好的充要条件.

定理1所有不含无差异关系的确定性偏好都是随机偏好空间的极端偏好,并且只有这些偏好是极端偏好.

证明显然在随机偏好空间Pπ（n）中,不含无差异关系的确定性偏好共有2C2n个,组成集合P= ｛π（cx≻cy）|x，y∈｛1，2，...，n｝，x＜y，π（cx≻cy）∈［0，1］｝.

证明过程分为下列充分条件和必要条件两部分进行.

1)充分条件

假设p∈P不是Pπ（n）中的极端偏好.由定义5可知,∃p1，p2∈Pπ（n）,且p1/=p2,∃ω∈（0，1）,使p= ωp1+（1-ω）p2成立,其中p1=｛π1（cx≻cy）｝,p2=｛π2（cx≻cy）｝.由此可知,∀x，y∈｛1，2，...，n｝且x＜y,必然有ωπ1（cx≻cy）+（1-ω）π2（cx≻cy）∈｛0，1｝,考虑到ω，1-ω∈（0，1）,因此π1（cx≻cy）=π2（cx≻cy）,即p1=p2,与p1/=p2矛盾.因此,p是极端偏好.

2)必要条件

设p*=｛π*（cx≻cy）|x，y∈｛1，2，...，n｝，x＜y｝/∈P是Pπ（n）中的极端偏好,则p*中至少存在一个偏好分量π*（cα≻cβ）/∈｛0，1｝.由定义5可知,∀p1，p2∈Pπ（n）且p1/=p2,∀ω∈（0，1）,使得p*= ωp1+（1-ω）p2都不可能成立.由于0=ω×0+（1-ω）×0≤ωπ1（cx≻cy）+（1-ω）π2（cx≻cy）≤ω×1+（1-ω）×1=1,因此只要保证π1（cx≻ cy）和π2（cx≻cy）不同时为0或1,必然有ωπ1（cx≻cy）+（1-ω）π2（cx≻cy）∈（0，1）成立.

基于上述分析可知,如果p*中有一部分偏好分量π*（cγ≻cτ）∈｛0，1｝,则相应地将p1和p2中的偏好分量π1（cγ≻cτ）和π2（cγ≻cτ）设置为0或1;p*中的其余偏好分量π*（cα≻cβ）/∈｛0，1｝必然可以表示为ωπ1（cα≻cβ）+（1-ω）π2（cα≻cβ）的形式,即相应地将p1和p2中的偏好分量分别设置为π1（cα≻cβ）和π2（cα≻cβ）.考虑到Pπ（n）是连续空间,因此只要p*/∈P,在Pπ（n）中p*的去心邻域Uo（p*，δ）内必然存在两个不同偏好p1和p2,使得∀x，y∈｛1，2，...，n｝且x＜y,∃ω∈（0，1）,π*（cx≻cy）=ωπ1（cx≻cy）+（1-ω）π2（cx≻cy）,即p*=ωp1+（1-ω）p2,因此p*不是极端偏好,这与假设矛盾.综上所述,∀p∈P都是随机偏好空间的极端偏好,而∀p/∈P都不是极端偏好.证毕.

由定义2可知Pπ（n）是有界空间,考虑到定理1给出Pπ（n）是凸偏好集的结论,因此Pπ（n）是有界凸偏好集.有界凸集上任意一点都可以用顶点凸组合表示,因此以极端偏好为基础,可以进一步定义一种完备的不确定偏好表示方法,如定义6所示.这里的完备性是指采用这种偏好表示方法可以表示偏好集内的所有可取偏好.

定义6随机偏好空间Pπ（n）中存在个极端偏好｛p1，p2，...，pk｝,vi∈V的个体偏好都可以表示为｛（πvi（p1），p1），（πvi（p2），p2），...，（πvi（pk），pk）｝这种形式,简记为pvi=pmid（p1，p2，...，pk）,其中πvi（pj）表示投票人vi选择极端偏好pj的概率,满足条件称pvi是投票人vi的一种基于极端偏好概率分布的不确定偏好,简称概率分布型随机偏好(stochastic preferencebased on probability distribution ofextreme preferences,SPPDEP).

需要注意的是,由于极端偏好的个数k与候选人数n呈指数型关系,SPPDEP中的极端偏好概率分布通常并不是主观设定的,甚至根本无法设定.分析例1可以看出,这种偏好表示方法在随机抽选等制度中可以得到较好地应用,此时极端偏好概率分布可以客观获取.另外,考虑到随机偏好只是对投票人个体偏好的一种预估,实际偏好往往都是确定性的,由此可知,极端偏好之间通常是互斥关系,即候选人选择了其中一个极端偏好就不能选择其他极端偏好,显然这个结论也可以从例1中得出.

3　概率分布型随机偏好下的Borda悖论

有了SPPDEP这种随机偏好表示方法,可以将Borda悖论中涉及的确定性概念和规则相应地推广到随机情况,在此基础上进一步研究随机偏好下的Borda悖论发生规律.

3.1两种随机投票规则

3.1.1随机捉对投票规则

本文所涉及的随机捉对投票规则(stochastic pairw isemajority rule,SPMR)与Grofman等［14］提出的思路基本相同,只是其中的随机偏好表示方法不同而已.

群认为cx≻cy的概率

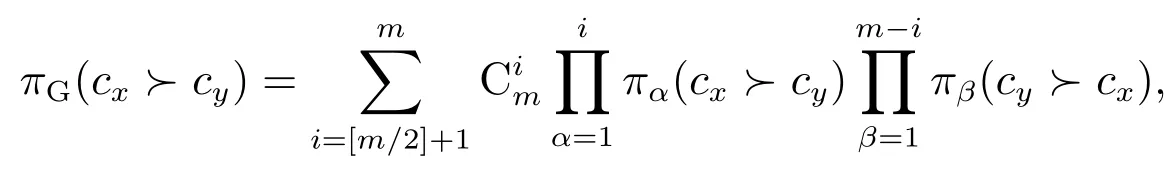
其中［m/2］表示对m/2做取整运算,α和β表示任意数量候选人的组合, cy｝∈pj）,l（｛cx≻cy｝∈pj）为示性函数,即

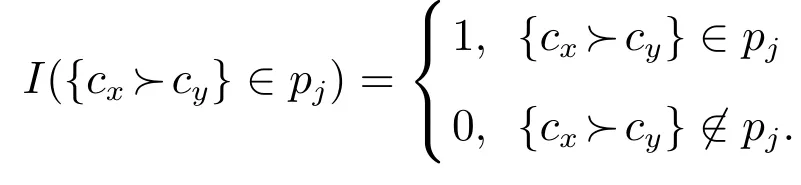
参考PMRL的定义,可给出随机捉对投票失败者(stochastic pairw isemajority rule loser,SPMRL)的概念.

定义7设cx，cy∈C,若∀cy/=cx,使得πG（cx≻cy）＜0.5都成立,则称cx是随机捉对投票失败者.

需要注意的是,对比文献[14]中的πG（cx≻cy）运算公式,SPPDEP在SPMR的运用SPSO反而要复杂一些.如果涉及到的问题仅限于SPMR,建议直接使用SPSO.

3.1.2随机排位投票制

PVR规定,权值向量W=（ω1，ω2，...，ωn）,其中ω1≥ω2≥···≥ωn,且ω1＞ωn,W中的第j个分量ωj的值分配给个体偏好中排名第j位的候选人.

在讨论随机排位投票制(stochastic positionalvoting rules,SPVR)之前,首先需要将SPPDEP中的极端偏好分为传递性和非传递性两类,不失一般性,设前n！项为传递性极端偏好.显然只有当非传递性极端偏好的概率都为0时,PVR才可以相应地推广.

在投票人vi的偏好分量pg中,候选人cx得分的数学期望其中表示vi的偏好分量pg中的第h位,为示性函数,即

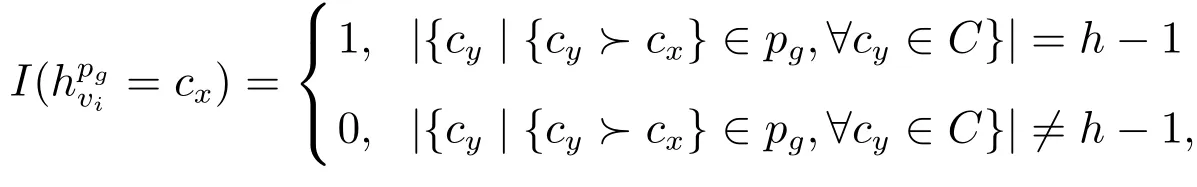
进一步可以推算出vi的偏好中cx得分的数学期望为由此可知cx得分的数学期望

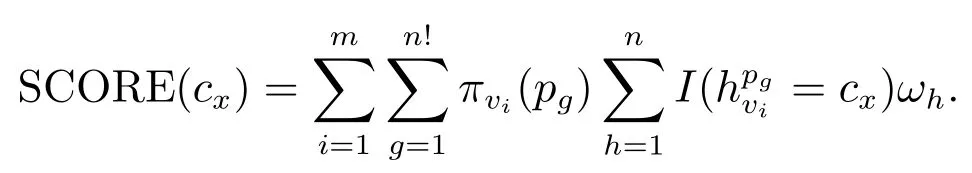
根据得分的数学期望大小关系可以给出群偏好序,数学期望越大的候选人在群偏好中的排名越靠前.

3.2概率分布型随机偏好下的Borda悖论

确定性偏好下的Borda悖论在线性权值向量的PVR中不可能出现,这一结论在随机情况下却不再成立.本节以三候选人为例对此进行论证.需要注意两点:1)Borda悖论下的SPMRL与3.1.1节略有不同,因为在这种情况下不讨论非传递性极端偏好部分,此时πG（cx≻cy）的运算公式不再是指数复杂度,而变成相对更简单的表达形式;2)本文仅讨论投票人数量m为不小于3的奇数情况,忽略了m为偶数时可能会涉及到候选人之间的平局处理问题.

首先引入两个引理[14],这是研究SPPDEP下Borda悖论发生规律的基础.

引理2在m个投票人的SPMR中,群偏好πG（cx≻cy）＞0.5的必要条件是1））（m+1）/2＞0.5,充分条件是

根据引理1和2,并综合3.1节提出的两种随机投票规则,可以给出下述结论.

定理2〈m，3〉群的随机投票问题中,线性权值向量的SPVR有可能产生Borda悖论.

证明〈m，3〉群的6个极端偏好如表2所示.

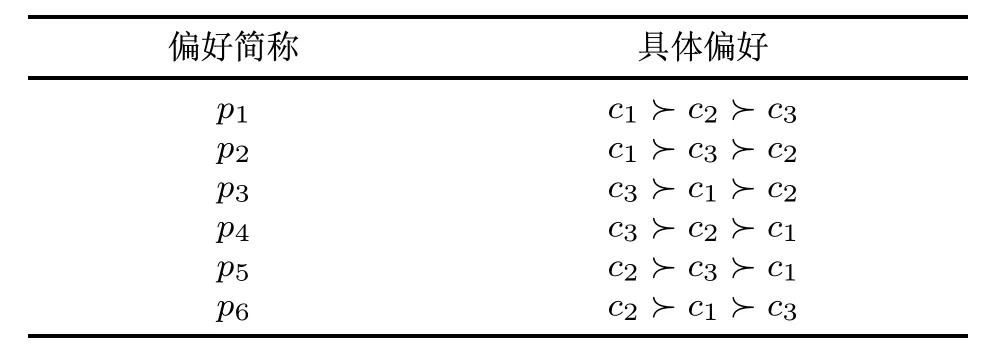
表2　三候选人偏好空间的极端偏好Table2　A llextreme preferences of three candidates’preference space

考虑到候选人间的对称性,不失一般性,设c1是SPMRL的同时也在SPVR中获胜.

由引理2可知,c1为SPMRL时需要满足条件

候选人得分的数学期望分别为

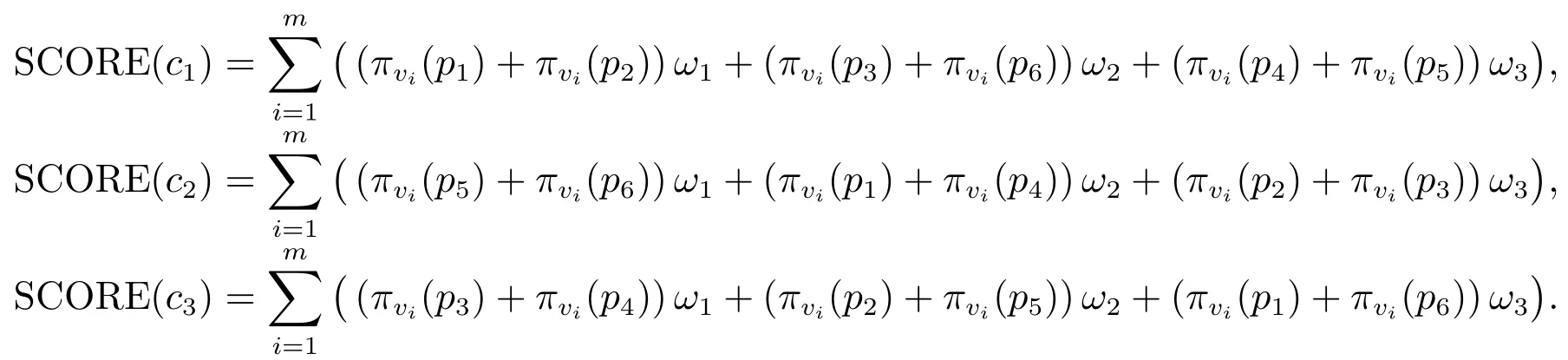
c1在SPVR中获胜时,需要满足条件

进一步化简得

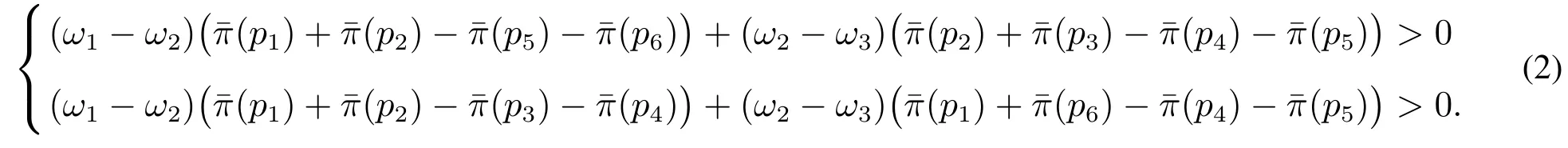
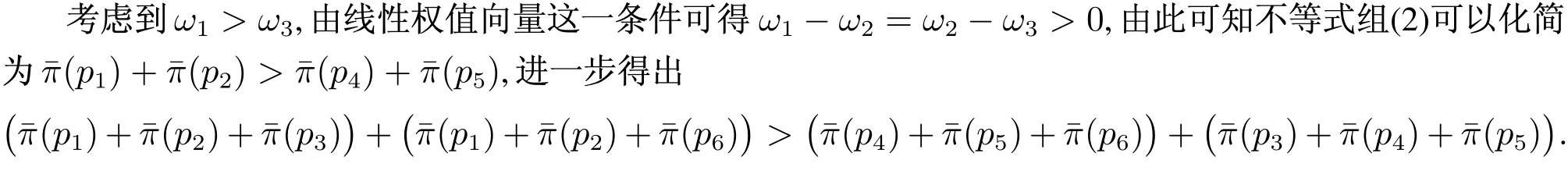
此时不等式组(3)与不等式组(2)不能同时成立,不可能产生Borda悖论.

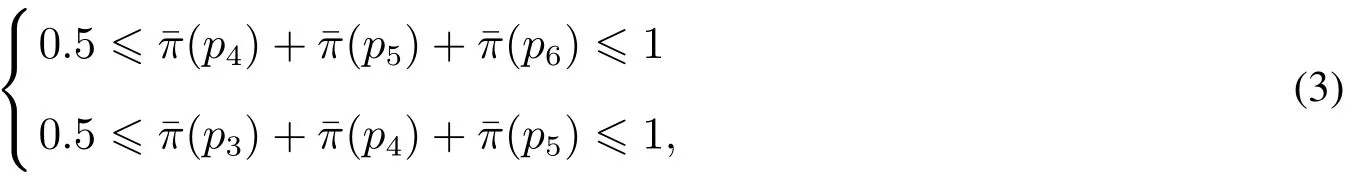
令f（m）=0.52/（m+1）（m+1）/（2m）,经运算可知,当m≥3时,f（m）与m正相关.考虑到0.5,由此可知在投票人数有限的情况下,不等式f（m）＜0.5必然成立.由此可知除不等式组(3)外还存在其他可以满足不等式组(1)的情况,具体可以分为式(4)～式(6),即

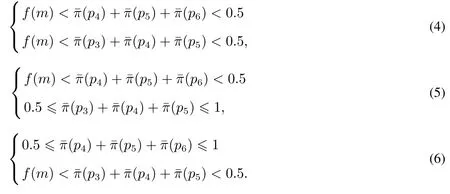
令g（m）=0.52/（m+1）（m+1）-（m-0.4）,经运算可知,当m≥3时,f（m）与m负相关.而= 1.4-2 ln 2,因此在投票人数有限的情况下,g（m）＞1.4-2 ln 2＞0,从而可知0.52/（m+1）（m+1）/（2m）＞0.5-0.2/m.由此可知（0.52/（m+1）（m+1）/（2m），0.5），［0.5，（m+1）/（2m）］⊆［0.5-0.2/m，（m+1）/（2m）］.

由引理1可知,如果¯π（cx≻cy）处于这两个区间,将（m-1）/2个投票人的概率设置为0,而其余（m+ 1）/2个投票人的概率设置为2m（cx≻cy）/（m+1）时,πG（cx≻cy）达到最大,=（2m¯π（cx≻ cy）/（m+1））（m+1）/2.m为常数时,随着（cx≻cy）单调递增,进一步运算可知＞ 0.5.若（cx≻cy）∈（（m+1）/（2m），1）,将（m+1）/2个投票人偏好的概率设置为1,此时= 1.因此,只要按照引理1的方法设置投票人的概率,无论¯π（cx≻cy）大于0.5还是小于0.5,＞ 0.5必然成立.

综上所述,〈m，3〉群的随机投票问题中,线性权值向量的SPVR有可能产生Borda悖论.证毕.

类似于PVR,非线性权值向量的SPVR也有可能产生Borda悖论.任意给定一个线性权值向量规则下的Borda悖论偏好断面,考虑到在满足约束条件｛ω1≥ω2≥ω3，ω1＞ω3｝的情况下SPVR中权值的取值在实数域内连续,因此可以保持ω2和ω3不变,将线性权值向量中的ω1进行微调,即足够小,仍然可以保证Borda悖论存在,此时权值向量变成非线性,因此非线性权值向量的SPVR有可能产生Borda悖论.Borda提出的经典〈21，3〉群偏好断面就是一个特殊的例子［2］.基于上述分析,可得下面的结论.

定理3〈m，3〉群的随机投票问题中,非线性权值向量的SPVR有可能产生Borda悖论.

综合定理2和定理3可知,3候选人情况下所有权值向量的SPVR都有可能产生Borda悖论.为便于理解这两个定理的含义,下面给出〈3，3〉群中SPVR产生Borda悖论的偏好断面示例.

例2给定一个偏好断面,如表3所示.

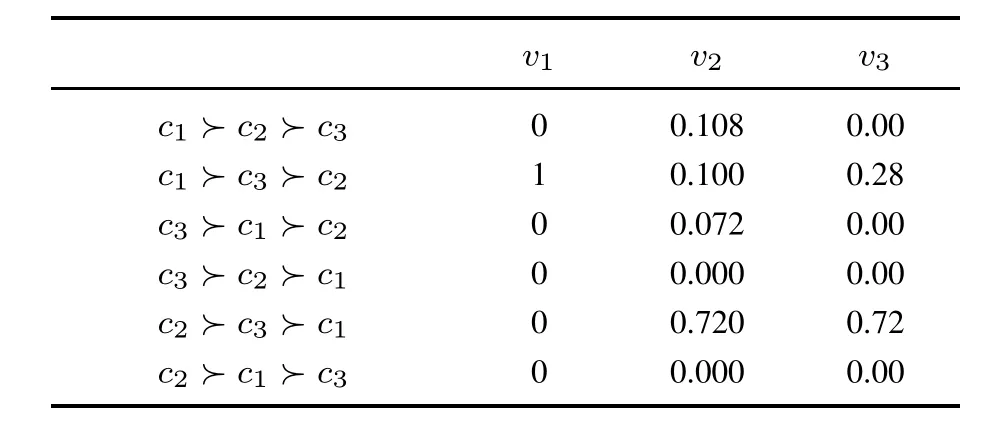
表3　〈3，3〉群的一个偏好断面Table 3　A profile of group〈3，3〉

由上述偏好断面运算可知,πG（c1≻ c2）=0.48160＜ 0.5,πG（c1≻ c3）=0.42976＜ 0.5,因此c1为PMRL.当SPVR中的权值向量为线性时,不妨设权值向量为（2，1，0）,此时SCORE（c1）=3.0480, SCORE（c2）=2.9880，SCORE（c3）=2.9640;当SPVR中的权值向量为（2.1，1，0）时,此时权值向量为非线性,SCORE（c1）=3.1968，SCORE（c2）=3.1320，SCORE（c3）=2.9712.显然在上述两种权值向量下c1获胜.c1作为PMRL在SPVR中获胜,因此无论权值向量为线性或非线性,SPVR都有可能产生Borda悖论.

3.3随机和确定性投票问题中Borda悖论发生规律的异同

随机偏好是确定性偏好在重复性决策中偏好不一致性的扩展表示.两者之间存在着一定的联系,也有明显的区别.因此,随机偏好和确定性偏好下Borda悖论的发生规律也存在相似和不同之处.考虑到Borda悖论的分析通常仅限于3候选人,因此与3.2节一样,本节仅讨论3候选人情况下悖论发生规律的异同.

从权值向量的角度分析.由定理2和3可知,〈m，3〉群的随机投票问题中,所有权值向量的SPVR都有可能产生Borda悖论,而这一结论在PVR中并不成立,因为线性权值向量的PVR不可能产生Borda悖论.出现这种差异的主要原因在于SPMR与PMR中πG（cx≻cy）＞0.5的必要条件不同.（cx≻cy）＜0.5时PMR中πG（cx≻cy）不可能大于0.5,而这种情况在SPMR中却有可能出现.

从投票人数的角度分析.∀m≥3,定理2和定理3都成立.而这一结论在确定性投票问题中却并不成立,也就是说PVR规则下Borda悖论存在与否与投票人数相关,具体分析如下.

在确定性投票问题中,偏好断面如表4所示,其中mi，i=1，2，...，6均为正整数

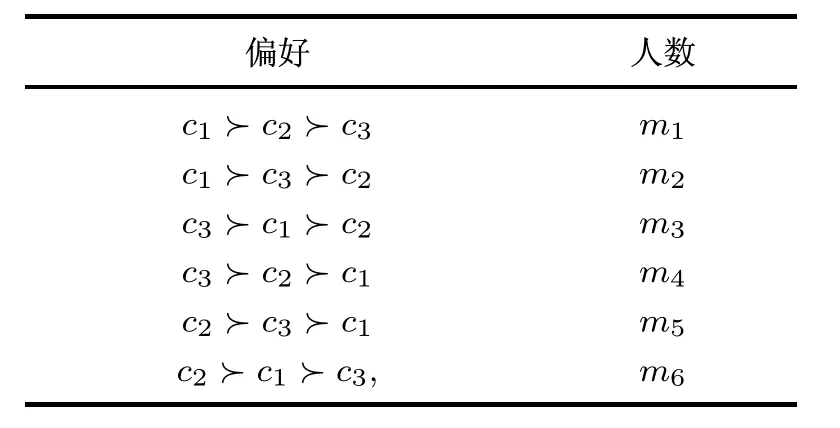
表4　确定性投票问题中的偏好断面Table4　The profile of determ inate voting problem

不失一般性,不妨设c1为PMRL,则有

若c1在权值向量为（ω1，ω2，ω3）的PVR中获胜,则有

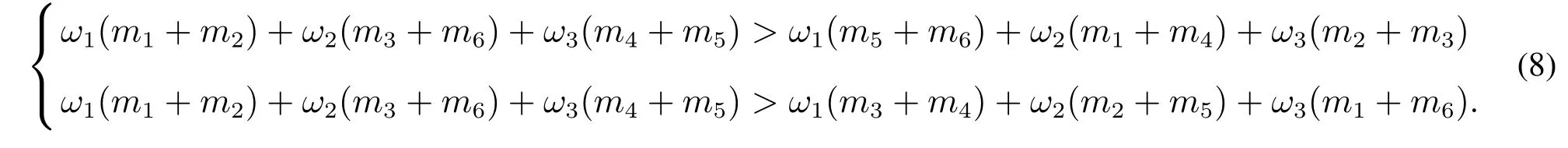
当总投票人数m足够小,如m=3或5时,无论（ω1，ω2，ω3）取什么值,式(7)和式(8)都不可能同时成立.

由此可知,在确定性投票问题中,并非∀m≥3,Borda悖论都存在,这一点也可以由文献[5,6]中的结论反映出来.出现这种差异的主要原因在于,m足够小时,确定性投票问题中可能的偏好断面足够少,且确定性偏好的定义域离散;而随机投票问题中无论m的大小,可能的偏好断面都有无穷多个,且随机偏好的定义域具有连续性.这种偏好断面数量上的巨大差异,以及偏好定义域的连续与否,导致了悖论发生规律在投票人数角度上的差异.

综上分析可得如下结论.

定理4〈m，3〉群的确定性投票问题中,Borda悖论的发生与否与PVR的权值向量、投票人数等因素相关;而随机投票问题中,Borda悖论的发生与否与这些因素无关,无论这些因素怎样变化,Borda悖论都有可能发生.

4　结束语

Borda悖论的发生规律在确定性投票规则中的理论分析和实证研究已经相对成熟,而在随机投票规则中的却比较少见.本文正是基于这一研究现状,提出一种随机偏好下Borda悖论的理论分析.

本文首先指出SPSO这种目前最常见的随机偏好表示方法在SPVR中存在不可回避的局限,在提出折中偏好和极端偏好等概念的基础上进一步给出SPPDEP表示方法.结合文章提供的例子可以看出,SPPDEP相比于SPSO不仅能更加具体地表达个体偏好,也能更准确地适用于非SPMR,尤其是SPVR这种随机投票规则.这也是进行随机偏好下Borda悖论分析的基础性工作.

以SPPDEP为基础,本文分别将PMR和PVR推广为相应的随机规则,分析了随机偏好下Borda悖论的发生规律,得出任何SPVR都有可能产生Borda悖论的结论,并将随机情况下的Borda悖论分析结果与确定性情况从权值向量和投票人数两方面进行对比,进一步分析两种情况出现差异的原因.

在研究随机偏好下Borda悖论是否发生的基础上,可以进一步研究Borda悖论的发生概率问题.考虑到随机偏好下的复杂性,不同于确定性情况的理论推导,可以采用计算机仿真的方法对不同文化条件［15］下的Borda悖论发生概率进行Monte Carlo仿真求解,这也是作者的下一步研究方向.

[1]GehrleinW V.Condorcet’sParadox.Berlin,Heidelberg:Springer-Verlag,2006.

[2]deBorda J.A paperon electionsby ballot//Sommerlad F.The Political Theory of Condorcet.Oxford:University ofOxford,1984: 122–129.

[3]G¨ardenfors P.Positionalistvoting functions.Theory and Decision,1973,4(1):1–24.

[4]Fishburn PC,GehrleinW V.Borda’s rule,positionalvoting,and Condorcet’ssimplemajority principle.Public Choice,1976,28(1): 79–88.

[5]GehrleinW V,Lepelley D.On the probability ofobserving Borda’sparadox.SocialChoiceandWelfare,2010,35(1):1–23.

[6]DissM,GehrleinW V.Borda’sparadox with weighted scoring rules.SocialChoiceandWelfare,2012,38(1):121–136.

[7]董玉成,徐寅峰,王扬.基于广义Fuzzy偏好关系的决策方法探讨.系统工程学报,2008,23(3):282–288. Dong Y C,Xu Y F,Wang Y.Study of decisionmakingmethod using generalized fuzzy preference relations.Journal of Systems Engineering,2008,23(3):282–288.(in Chinese)

[8]姚爽,郭亚军,黄玮强.一种语言评价信息不完全的多属性群决策方法.系统工程学报,2011,26(4):460–467. Yao S,Guo Y J,Huang W Q.An approach of multi-attribute group decisionmaking with incomplete linguistic assessment information.Journal of Systems Engineering,2011,26(4):460–467.(in Chinese)

[9]Tversky A.Intransitivity of preferences.PsychologicalReview,1969,76(1):31–48.

[10]Myung IJ,Ramamoorti S,Bailey A D.Maximum entropy aggregation of expert predictions.Management Science,1996,42(10): 1420–1436.

[11]Regenwetter M,Dana J,Davis-Stober CP.Transitivity of preferences.Psychological Review,2011,118(1):42–56.

[12]Ye F,Dong N,Li J,etal.The sufficient and necessary condition of themajor stochastic preference rule in group decisionmaking. Journal of Systems Science and Complexity,2012,25(5):942–949.

[13]Gilboa I.A necessary butinsufficientcondition for the stochastic binary choiceproblem.Journal of Mathematical Psychology,1990, 34(4):371–392.

[14]Grofman B,Owen G,Feld SL.Thirteen theorems in search of the truth.Theory and Decision,1983,15(3):261–278.

[15]Gehrlein W V,Lepelley D.Voting Paradoxes and Group Coherence:The Condorcet Efficiency of Voting Rules.Berlin,Heidelberg: Springer-Verlag,2011.

Borda’sparadox under stochastic preference

Wu Fan1，2,Zhao Yong1,Chen Huangqiong3
(1.Institute of Systems Engineering,Huazhong University of Science and Technology,Wuhan 430074,China;
2.Jiangsu Posts&Telecommunications Planning and Designing Institute Co.,Ltd.,Nanjing 210019,China;
3.Patent Examination Cooperation Jiangsu Center of the Patent Office,SIPO,Suzhou 215163,China)

On thebasis of illustrating theweaknessof stochastic preferencesbased on strictorder(SPSO),this paper proposesamore universal representation which is called stochastic preference based on the probability distribution of extreme preferences(SPPDEP),and demonstrates the completeness of SPPDEP,i.e.,SPPDEP can representall feasiblestochasticpreferences.With SPPDEP,itextendstwovoting rulesreferred toasBorda’s paradox into stochasticmode,and analyzes the occurrence regularitiesof Borda’s paradox in thismode.Furthermore,comparing with the occurrence regularities of Borda’s paradox in determinatingmode,it discusses the similarities and differencesbetween the twomodes,and analyses for the reasons for those differences.

Borda’sparadox;stochastic preference;probability distribution;stochastic voting rules

C934

A

1000-5781(2016)02-0145-10

10.13383/j.cnki.jse.2016.02.001

2014-05-22;

2015-03-19.

国家自然科学基金资助项目(61273206;71071063).

吴凡(1988—),男,安徽马鞍山人,博士生,研究方向:群决策理论,方法及应用,Email:dragonwufan@126.com;

赵勇(1966—),男,湖北天门人,博士,教授,研究方向:群决策理论,方法及应用,Email:zhiwei98530@hust.edu.cn;

陈煌琼(1984—),女,湖北咸宁人,博士生,研究方向:社会选择理论,Email:chqkhs@163.com.