巧用数学思想妙解一次函数
□曹 洪
巧用数学思想妙解一次函数
□曹洪

一、转化思想
例1(2015·桂林)如图1,直线y=kx+b与y轴交于点(0,3),与x轴交于点(a,0),当a满足-3≤a<0时,k的取值范围是().
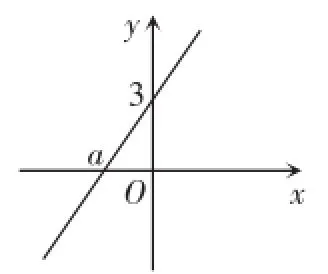
图1
A.-1≤k<0 B.1≤k≤3
C.k≥1 D.k≥3
分析:把点的坐标代入直线解析式得到,然后将其代入不等式-3≤a<0,将其转化为关于k的不等式,即可求出k的取值范围.
解:把点(0,3)和(a,0)代入y=kx+b,得b=3,
故选C.
点评:把点的坐标代入直线解
二、数形结合思想
例2(2015·徐州)若函数y= kx-b的图象如图2所示,则关于x的不等式k(x-3)-b>0的解集为().
A.x<2 B.x>2
C.x<5 D.x>5

图2
分析1:由图2可知一次函数图象过点(2,0),将其代入一次函数解析式,可求出k、b的关系式,然后将k、b的关系式代入k(x-3)-b>0中解不等式即可.
运动控制系统是一门实践性非常强的课程,本质上是面向工程的,但是在实际教学中,由于教学要求和培养模式的限制,无法使课程直接面向工程实际,这对一门实践性强的课程来说,学习效果会大打折扣。因此,在运动控制系统课程教学中尝试面向工程实际,通过实际的工程项目,使学生对课程的应用性有更加深刻的认识。本项目目前在申请学校的教改课题,将复杂的工程问题嵌入课堂教学中,达到理论联系实际、实践促进理论的目的。
解1:∵一次函数y=kx-b的图象过点(2,0),
∴2k-b=0,b=2k.
由图2可知,函数值y随x的增大而减小,∴k<0.
将b=2k代入k(x-3)-b>0,得k(x-3)-2k>0,即kx>5k,两边同除以k得x<5,故选C.
分析2:∵一次函数y=kx-b的图象向右平移3个单位得到一次函数y=k(x-3)-b的图象,
∴由函数y=kx-b的图象与x轴交点的坐标可得到函数y=k(x-3)-b与x轴交点的坐标,进而通过图象得到关于x的不等式k(x-3)-b>0的解集.
解2:∵一次函数y=kx-b的图象向右平移3个单位得到一次函数y=k(x-3)-b的图象,由一次函数y= kx-b的图象与x轴交点坐标为(2,0),可以得到一次函数y=k(x-3)-b的图象与x轴交点坐标为(5,0)(如图3).

图3
点评:解决此类问题的关键是仔细观察图形,注意几个关键点(交点、原点等),数形结合思考问题.
三、整体思想
例3若y+b与x+a(a、b为常数)成正比例,当x=3时y=5,当x=2时y=2,求y关于x的函数关系式.
分析:根据y+b与x+a(a、b为常数)成正比例,列出关系式y= kx+(ka-b),再将两对x、y的值代入,求出待定系数,但需要把其中的(ka-b)当做一个整体来处理.
解:由条件可得y+b=k(x+ a),即y=kx+(ka-b).
因为x=3时y=5,x=2时y=2,

所求函数解析式是y=3x-4.
点评:因直接求出a、b的值是比较困难的,这里应用了整体思想,整体求出ka-b的值.

