脉冲Leslie-Gower型捕食者-食饵系统的概周期解

钟 丽 华

(北华大学数学与统计学院，吉林 吉林 132013)



脉冲Leslie-Gower型捕食者-食饵系统的概周期解

钟 丽 华

(北华大学数学与统计学院，吉林 吉林 132013)

考虑了食饵具避难效应的脉冲Leslie-Gower型生物系统.利用相应的常微分方程系统解和脉肿系统解的关系，得到脉冲生物系统的持久性及唯一概周期解的存在性.

脉冲系统；Leslie-Gower型捕食者-食饵模型；概周期解；持久性

近年来脉冲微分方程由于其精准描述系统发展遭遇扰动的特征而得到众多学者的广泛研究，其相关基本概念及有关脉冲生物模型的研究成果可参见文献[1-6].

另一方面，现实世界概周期环境因素的存在也值得关注，文献[4-5]研究了周期和概周期竞争生物系统模型.受此启发，本文研究一个重要的食饵具有避难效应的脉冲Leslie-Gower型系统

(1)

文献[4，7-8]讨论了这个模型周期解的存在性和分支问题.本文主旨是利用相应常微分方程系统的解和脉冲系统的解的关系，考虑脉冲系统(1)概周期解的存在性问题.

1　模型分析

定义1.2[6]函数φ∈PC(R，R)称为概周期的，如果它满足下面的条件：

(2) 对于任意的ε>0，存在实数δ>0，当t′-t″<δ时，φ(t′)-φ(t″)<ε.

(3) 对ε>0，存在一个相对稠密集合T，如果对τ∈T，当φ(t+τ)-φ(t)<ε时，有t-τk>ε，k∈Z.

考虑系统：

(1.1)

引理1.1yi(0)>0，令(yi(t),y2(t))T是系统(1.1)的解，则对于所有t≥0，满足yi(t)>0(i=1，2).

引理1.2系统(1)和(1.1)满足下列关系：

(1) 如果(y1(t)，y2(t))T是系统(1.1)的解，则

是(1)的解；

(2) 如果(x1(t),x2(t))T是(1)的解，则

是(1.1)的解.

当t=τk,k=1,2,…,有

(1.2)

所以方程(1)最后两个等式也成立.因此(x1(t)，x2(t))T是方程(1)的解.

所以yi(t)在区间[0，+∞)是连续的.易知(y1(t)，y2(t))T满足系统(1.1).

引理1.3假设：

(H1) 存在正常数mi和Mi，当t>0和1+hik>0(i=1，2)时，

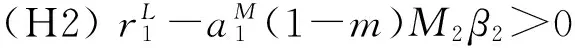
则方程(1.1)的解满足

其中

证明令(y1(t),y2(t))T是方程(1.1)的解.由假设条件知

利用比较原理，

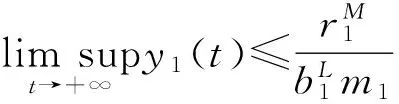
从而对于任意的正数ε，存在T1>0，当t>T1时，

y1(t)<β1+ε.

(1.3)

再由(1.1)式的第二个方程和(1.3)式，当t>T1时有

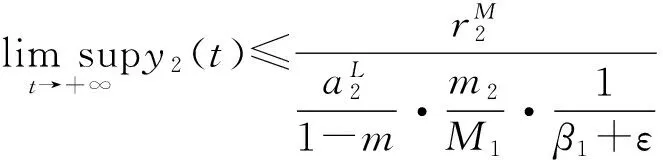
即对于任意的正数ε，存在T2>T1，当t>T2时，

y2(t)<β2+ε.

(1.4)

另一方面，由(1.1)式的第一个方程和(1.4)式，当t>T2时，

令ε→0，可以得到

即对于任意的正数ε，存在T3>T2满足当t>T3，有

y1(t)>α1-ε.

类似地，对于足够大的t，

令ε→0，可以推出

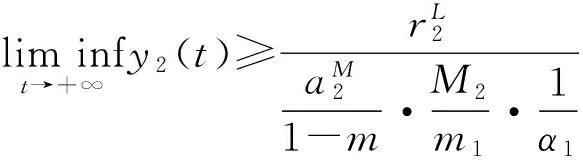
引理证明完成.

注1.1在引理1.3的条件下，集合

Ω={(y1，y2)T∈R2|0<αi≤yi≤βi，i=1，2}

是系统(1.1)的不变集，从而系统是持久的.

引理1.4假设(H1)和(H2)成立.则系统(1.1)的解(x1(t),x2(t))T满足

(1.5)

证明由引理1.2，(x1(t)，x2(t))T是系统(1)的解，则

是系统(1.1)的解.由引理1.3得

(1.5)式成立意味着系统(1)是持久的.

引理1.5假设(H1)和(H2)成立，那么集合Ω≠∅.

证明利用概周期函数的性质，存在序列{tn}，当n→∞时tn→∞，且n→∞时，

ri(t+tn)→ri(t)，Ai(t+tn)→Ai(t)，B1(t+tn)→Bi(t)，i=1，2

在R一致成立.

取(y1(t)，y2(t))T作为(1.1)的解，满足对于充分大的正常数T*和i=1，2，αi≤yi(t)≤βi，且序列{y(t+tn)}在R的有界子集上是一致有界且等度连续的.由Ascoli定理，当k→∞时，存在子列{y(t+tnk)}，其在R的有界子集一致地收敛到连续函数族zi(t)，从而对于给定的Ti∈R，假设对所有的nk，tnk+T1≥T*.考虑下列系统：

B1(s+tnk)y1(s+tnk)-A1(s+tnk)(1-m)y2(s+tnk)]}ds，

y2(t+tnk+T1)=y2(tnk+T1)+

由Lebesgue控制收敛定理，令k→∞，对于t≥0，

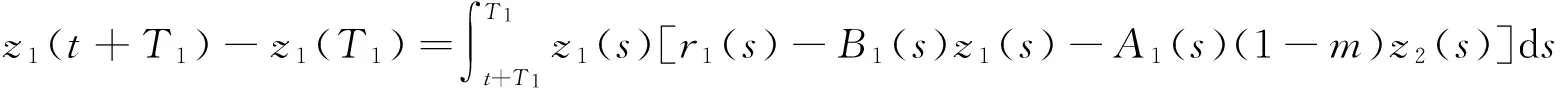
(1.6)

因为T1是任意的，(z1(t)，z2(t))T是(1.1)的解.显然，对于t∈R和i=1，2，有αi≤zi(t)≤βi，所以(z1(t)，z2(t))T∈Ω.

2　主要结果

考虑常微分方程

(2.1)

其中D是Rn中的开集，f(t,X)对于X∈D关于t是一致概周期的.为讨论(2.1)概周期解的存在性，考虑方程(2.1)的积系统

引理2.1[6]假设存在一个定义在[0，+∞)∈D×D的Liapunov函数V(t，X，Y)，满足下列条件：

(1)α(‖X-Y‖)≤V(t,X,Y)≤β(‖X-Y‖)，其中α(γ)和β(γ)是连续递增的正定函数；

(2) |V(t,X1,Y1)-V(t,X2,Y2)|≤K{‖X1-Y2‖+‖Y1-Y2‖}，其中K>0是一个常数；

(3)V(t,X,Y)≤-μV(t,X,Y)，其中μ>0是一个常数.

且对于所有t≥0，t0≥0，在紧集Ω⊂D⊂R2中方程(2.1)有解.则方程(2.1)在Ω中有唯一的概周期解，其在D中是一致渐近稳定的.

定理2.1假设引理1.3的条件(H1)和(H2)满足，同时下列条件成立：

(H5) 存在正常数ρ1，ρ2，θ满足

则系统(1)存在唯一概周期解.

证明首先证明方程(1.1)有唯一的概周期解.

(2.3)

所以系统(1.1)的概周期解的存在性等价于系统(2.3)在Ω1={(z1,z2)T∈R2|lnαi≤zi≤lnβi，i=1，2}有唯一的概周期解，并且Ω1关于系统(2.3)是不变的.

(2.4)

显然有

min{ρ1,ρ2}‖Z(t)-Z*(t)‖≤V(t,Z(t),Z*(t))≤max{ρ1,ρ2}‖Z(t)-Z*(t)‖，

所以引理2.1的条件(1)满足.注意到

从而引理2.1的条件(2)也满足.

利用方程(2.4)的解计算右导数D+V(t)，有

D+V(t)=

其中用到了中值定理和条件(H1).进而

假设系统(1)中hik≡0，i=1，2；k=0，1，2，….考虑系统特殊的非脉冲点的常微分方程：

(2.5)

推论2.1假设下面条件成立：

其中

则系统(2.5)有唯一的概周期解.

[1]SAMOILENKO A M，PERESTYUK N A.Impulsive differential equations[M].Singapore：World Scientific，1995：1-270.

[2]YOSHIZAWA T.Stability theory and the existence of periodic solutions and almost periodic solutions[M].New York：Springer，1975：40-223.

[3]DONG LINGZHEN，CHEN LANSUN.A periodic predator-prey chain system with impulsive perturbation[J].J Comput Appl Math，2009，223：578-584.

[4]HUO HAIFENG,LI WANTONG.Periodic solutions of delayed Leslie-Gower predator-prey models[J]Applied Mathematics and Computation，2004，155：591-605.

[5]SHAIR AHMAD，GANI TR STAMOV.Almost periodic solutions ofN-dimensional impulsive competitive systems[J].Nonlinear Anal：Real World Appl，2009，10(3)：1846-1853.

[6]HE MENGXIN，CHEN FENGDE，LI ZHOUNG.Almost periodic solution for an impulsive differential equation model of plankton allelophthy[J].Nonlinear Anal：Real World Appl，2010，11：2296-2301.

[7]KUMAR KAR T.Stability analysis of a prey-predator model incorporating a prey refuge[J].Communications in Nonlinear Science and Numeric Simulation，2005，10：681-691.

[8]CHEN FENGDE，CHEN LIUJUAN，XIE XIANGDONG.On a Leslie-Gower predatorprey model incorporating a prey refuge[J].Nonlinear Analysis：Real World Applications，2009，10：2905-2908.

(责任编辑：李亚军)

Almost periodic solutions of an impulsive Leslie-Gower prey-predator system

ZHONG Li-hua

(School of Mathematics and Statistics，Beihua University，Jilin 132013，China)

Impulsive Leslie-Gower predator-prey model incorporating a prey refuge is considered.Using the relation between the solutions of impulsive system and the corresponding non-impulsive system，sufficient conditions ensuring the permanence of non-impulsive system and the existence of a unique almost periodic solution are obtained.

impulsive system；Leslic-Gower prey-predator model；almost periodicity；permanence

1000-1832(2016)03-0048-06

2015-05-13

国家自然科学基金资助项目(11271157；11371169).

钟丽华(1973—)，女，讲师，主要从事微分方程研究.

O 211.63[学科代码]110·44

A

[DOI]10.16163/j.cnki.22-1123/n.2016.03.010