一种基于融合核函数支持向量机的遥感图像分类
古丽娜孜·艾力木江,孙铁利,乎西旦
(1.伊犁师范学院电子与信息工程学院,新疆 伊宁 835000;2.东北师范大学地理科学学院,吉林 长春 130024;3.东北师范大学计算机科学与信息技术学院,吉林 长春 130117)
一种基于融合核函数支持向量机的遥感图像分类
古丽娜孜·艾力木江1,2,孙铁利3,乎西旦1
(1.伊犁师范学院电子与信息工程学院,新疆 伊宁 835000;2.东北师范大学地理科学学院,吉林 长春 130024;3.东北师范大学计算机科学与信息技术学院,吉林 长春 130117)
从核函数选取规则着手,结合遥感数据本身特征,将具有互补性的几种核函数融合在一起,提出了一种复合核函数构造方法.通过实验数据与传统支持向量机方法比较,结果表明了复合核方法的有效性.
支持向量机;遥感数据;核函数;光谱
遥感图像的分类是遥感数据研究领域的重要部分,如何解决并提高样本间的分类精度是遥感数据应用的关键,具有较强的实际研究意义.
遥感数据技术通过获取大尺度、动态、宏观的各类专题图,对土地覆盖检测提供有利的数据.与此同时,由于地理空间数据的不确定性和复杂性等特征,异物同谱现象和同物异谱现象,使得专题图数据表达得有些模糊和不确定性,从而加大了信息提取工作的难度.[1-3]精确与时时地土地覆盖分类遥感数据的提取不仅与数据质量和分辨率有关,同样也与分类技术有关[4-5].因此,提高遥感数据分类精度已经引起了很多人对遥感研究领域的关注[6-7].基于统计模式的分类方法,Vapnik提出支持向量机(SVM)方法,以计算量较低而在非线性分类问题很受欢迎并成为热点的研究算法,也是模式识别领域最为活跃的一个机器学习算法.[6-9]同样在维数高、数据不确定性等遥感数据处理领域里也显出了其优势[10-12].目前,SVM不管是在图像分类[13-14],还是在土地覆盖分类、森林类型检测、农业作物监测、道路信息提取等领域都被广泛使用[15-22].尽管如此, SVM分类方法仍有进一步优化改进并完善的研究空间,这跟SVM 本身设计原理息息相关.当要解决具体问题时,首先应考虑数据集的特征和分类问题的性质,如果核函数的选择及其参数选定不当,则将直接影响分类结果,有的需靠经验知识,有的只能自己手工调整.
不管是哪一类核函数,它的性能一般就在核函数的本身.因此,特定领域的分类问题靠核函数的选择及其他的参数.若随意地选了核函数,则该核函数模型的推广性将会受影响,甚至影响到样本的分类效率.[23-27]所以,针对特定的数据集和数据来源,根据先验知识和经验,选择合适的核函数,分类精度必然会提高.
本文提出一种根据核函数本身的性质与构造原理来构建复合核函数.应用SVM在进行图像分类时,基于线性核、多项式核、径向基核、感知器核(S型核)的分类结果与本文提出的复合核函数下的分类结果进行了对比研究.
1 SVM学习方法
SVM是统计学习理论中最重要的学习方法,仅从分类的角度来分析的话,SVM是一种广义的线性分类器,在该分类器的基础上,经过引入结构风险最小化、最优化和核方法等原理与理论逐渐演化而成的.虽然该方法的设计完成经历了从1992年到1995年的漫长的3年时间,但从实用角度来看,目前仍处于不断完善、优化的阶段.
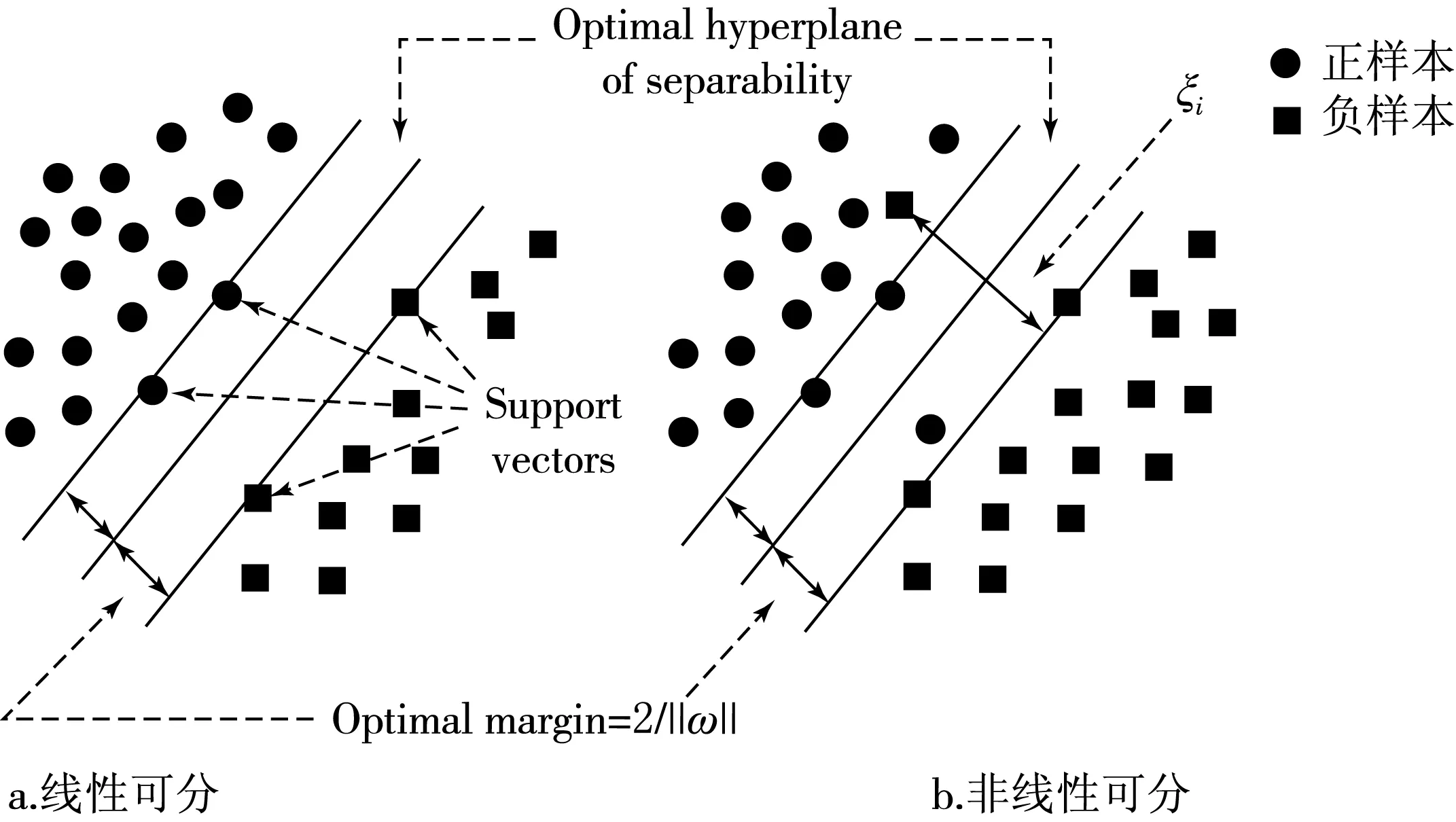
图1 二维情形中的最优分类面和间隔(Margin)
SVM的工作原理就是一个分类面(分类曲线或者是分类线).简单线性可分的两类问题上它就是一条分离线或者是分类曲线;多类复杂的,即为非线性可分情况下它就是一个分类面,当在这种复杂情况下,它先通过运用适当的内积函数也就是核函数,将输入空间中的输入点信息映射到其他某个高维的空间中,使得输入样本在这里能线性可分,从而求出可分所对应的最优线性分类面.所谓最优指的是不同样本之间的分类间隔最大,使得不同样本能正确分开(如图1所示).
SVM的线性可分分类问题描述为
s·t·yi[wxi+b]-1≥0,i=1,2,…,l.
(1)
其训练样本集为
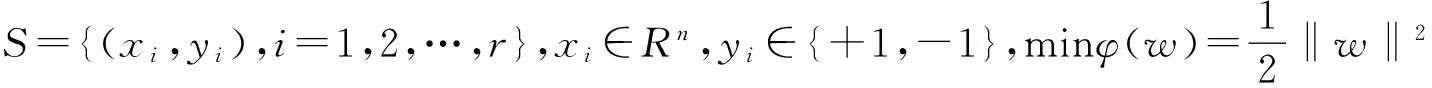
(2)
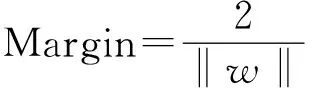
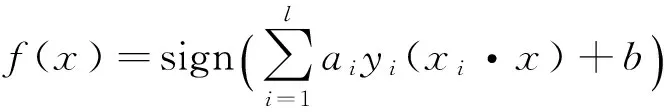
(3)
其中对应ai≠0的样本就是支持向量.
解决非线性图像分类问题时,利用一些非线性特征变换,将原始输入空间中的输入点信息转变(映射)到其他的某个高维特征空间中去,然后到这新的空间中求出最优的分界面.根据映射(2)式可变为:
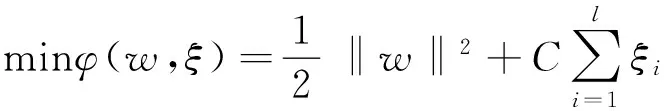
s·t·yi[wxi+b]-1+ξi≥0,i=1,2,…,l,ξi≥0,i=1,2,…,l.
(4)
其中φ( )为空间变化函数,C为惩罚系数,ξi为松弛项.
通过运用与构造不同形式的核函数,就可解决不同的分类问题,这样最优分类面(3)式引入核函数后变为
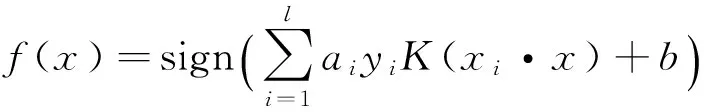
(5)
2 核函数与选取方法
2.1核函数
核函数本身就是一个通过内积运算将各类线性算法非线性化的点积运算公式.核函数理论研究已有很长的历史,但是,在Vapnik等人将核函数思想用到SVM方法之前,核函数的重要性其实没有受到很大重视,运用较欠缺.
SVM被提出之后,很多人就意识到原来提高SVM分类精度的关键就是选择和确定合适的核函数及其参数的选择,继而基于核函数的各类算法的设计以及相关领域里的应用应运而生.
根据核函数的定义和构造原理来分析的话,核函数的选择问题并不困难,只要满足Mercer定理的函数都可以当做核函数来使用.SVM中常用的核函数有以下几种:
(1) 线性内核为K(x,xi)=x·xi;
除了这些简单核函数以外,目前研究主要集中在根据具体数据集构造复杂的核函数,使得SVM能够得到进一步的推广.
2.2核函数的基本性质
2.2.1封闭性
若k1,k2,k3,…是核函数,则有:
(a)k1+k2是核函数;
(b)αk1,α≥0是核函数;
(c)k1∘k2是核函数;
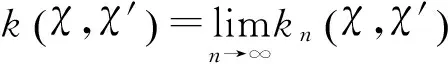
2.2.2组合性
设k:Χ×Χ→R是核函数,f:Χ→R是任意核函数,则有:


2.2.3正定性
k:Χ×Χ→R是核函数当且仅当它是正定的.
2.2.4无关性
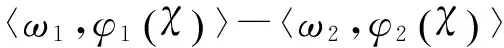
2.2.4相似性
核函数本身就是一个测度函数,是根据输入样本之间的相似性而设置的特征映射,即距离公式.对于核函数k:Χ×Χ→R的特征映射φ,该距离公式为
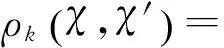

这个距离公式就是计算χ与χ′等两类样本之间的相似性度量,这一点理解核函数和SVM是非常重要的.比如,在遥感数据的分类工作中,关注样本之间的光谱相似性特征是极其重要的.
2.3核函数方法实现步骤
核函数方法是由核函数设计和算法设计等两大模块组成的一种模块化的方法,其具体过程如图2所示.
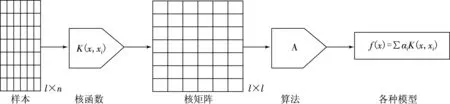
图2 核函数方法实现步骤
核函数方法的实现步骤,可以概括为:
(1) 样本采集并标准化;
(2) 选择或构造恰当的核函数;
(3) 将输入数据通过非线性变换函数映射到高维特征空间,即用核函数将输入样本变换成为核函数矩阵信息,这个步骤非常关键,注意矩阵是l×l的对称矩阵,l为样本数;
(4)最后在对称矩阵上使用一些线性方法,可得原输入空间中的所对应的非线性模型.
2.4目标核函数——复合核函数
依据:(1)SVM核函数中用的较多的是径向基核,因与其他常用核相比,径向基核的参数较少,比较容易掌握.只要保证σ→0,样本基本都能区分,正确分类.(2)多项式核一来简单,二来随着阶数d值的变小而增强,因此它的推广能力较强.(3)只要保证展开项数不多的任何正弦、余弦等连续可微的周期函数都可以用多项式来逼近,而且选取傅里叶核可以使SVM达到较好的推广性能,由此可以设想用这一类核函数去逼近其他类型的核函数.当然,这些核都有各自突出的优点和不足之处,一旦将它们组合起来应用就可以达到互补的效果.由此我们将它们自然地组合起来,构成一个复合核函数,应用到实际的遥感影像分类问题中.
为了引入重点的方便,不妨使用如下符号,令:
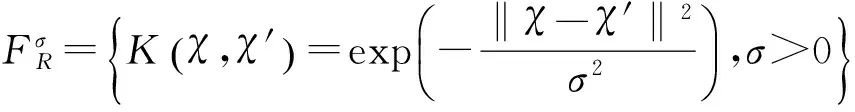
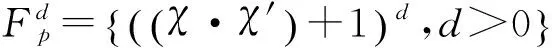

利用核函数的“封闭性”性质,构造出复合核函数为

(6)
其中ρi称为权参数,代表着这三类核函数在复合核函数中占的比例,而d,σ和q均为核参数.从(6)式看出,当ρ1=1,ρ2=ρ3=0时,(6)式就转变为常用的径向基核,而当ρ2=1,ρ1=ρ3=0时,(6)式就是简单的多项式核.这点有利于我们选取核参数d.
(6)式中的参数比较复杂,所以我们首先选取核参数最优值,然后再去选择权参数最优值.
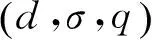
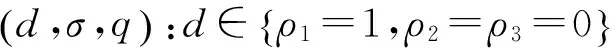
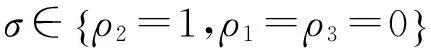
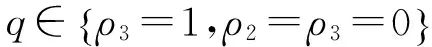
对于核参数最优值的选择,目前有很多种方法,如交叉验证、遗传算法、网络搜索法、平均约束规划(MPEC)模型[28]等.我们采用传统的遗传算法获取最优的核参数值.
3 实验结果及分析
本文采用2009年12月18日制作的吉林长春伊通河ALOS数据,覆盖范围长达10.074 13m×10.115 708m地段,由7 100 行7 995列4个波段([BIP]式)组成,含227,123,619B像素.为了实验的方便截取1 014像素×721像素×3像素规格的一部分数据当做本次实验数据集.数据集大致分为由水体、建筑、草地与灌木、裸地、道路等5类,以下是实验样本集,感兴趣区域样本间分离度的数字化和可视化表示形式见图3—5.
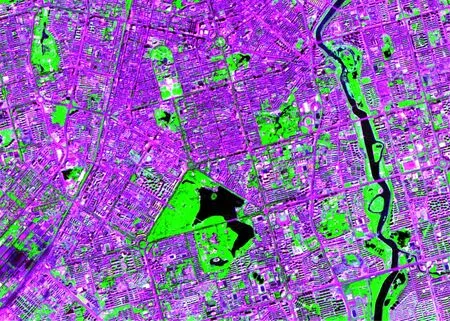
来自于2009-12制作的吉林长春伊通河遥感影像

图4 ROI样本分离性报告

图5 ROI样本分类型n-D可视化报告
实验结果和分类效果见表1和图6.更换了复合核以后,样本间的分类精度从Kappa系数、总体分类精度、分类可视化效果等都有所提高.但这效果也是换取结构复杂、所需参数较多的核函数为代价,所以这样复杂的结构势必会增加算法的时间复杂度,这正是课题组下一步将要研究解决问题,将使算法达到结构上的鲁棒性.

表1 实验结果
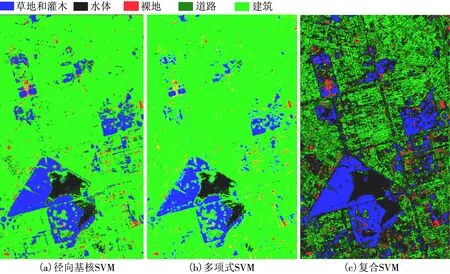
图6分类效果图
文献报道到遥感数据感兴趣区域里每类样本之间的区分度都在1.8以上,比较理想,而我们实验数据仅达到1.554 6.但从整体来说,以核函数的角度来看,我们获得实验数据已达到构建核函数的目的,以后加以改进优化等工作作为下一步的研究任务.
4 结语
本文利用核函数的封闭性、组合性等固有性质和SVM 方法的常用核函数技巧构建了一种复合核函数,实验数据表明,该方法具有一定的推广性能.但仍有一些不足:(1)核函数的结构较为复杂;(2)没能加上样本的光谱特征,因我们的实验数据源就是遥感数据,所以对遥感数据来讲得兼顾样本之间的光谱特征才行,也就是说普通距离运算和光谱运算结合起来当做样本之间的距离运算,这样样本间的区分度会更好一些,这也是将来要研究完成的任务之一.
[1]SERGE A, LUDOVIC R,YANNICK C,et al. A fuzzy-possibilistic scheme of study for objects with indeterminate boundaries:application to French Polynesian reef scapes[J].IEEE Transaction on Geoscience and Remote Sensing,2000,38(1):257-270.
[2]YANG C,BRUZZONE L,SUN F Y,et al.Fuzzy statistics based affinity propagation technique for clustering in multis images [J]. IEEE Transactions on Geoscience and Remote Sensing,2010,48(6):2647-2659.
[3]骆继成,郭华东,史文中,等. 遥感数据的不确定性问题[M]. 北京:科学出版社,2004:97-264.
[4]YOUSSEF A M. An enhanced remote sensing procedure for material mapping in the western desert of Egypt:a tool for managing urban development [J]. Natural Resources Research,2008,17(4):215-226.
[5]PAN X,ZHANG S Q,ZHANG H Q.A variable precision rough set approach to the remote sensing land use/cover classification [J]. Computers & Geosciences,2010,36(14):66-1473.
[6]ROGÉRIO GALANTE NEGRI,LUCIANO VIEIRA DUTRA,SIDNEI JOO SIQUEIRA SANT’ANNA. An innovative support vector machine based method for contextual image classification [J]. ISPRS Journal of Photogrammetry and Remote Sensing,2014(87):241-248.
[7]VAPNIK V N.Statistical Learning Theory [M]. New York:Wiley,1998:132-302.
[8]JIA X P,KUO B C,CRAWFORD M M. Feature mining for hyperspectral image classification [J]. Proc IEEE,2013,101(3):676-697.
[9]WANG L,JIA X. Integration of soft and hard classifications using extended support vector machines [J]. IEEE Geoscience and Remote Sensing Letters,2009,6(3):543-547.
[10]DALPONTE M,BRUZZONE L,GIANELLE D. Fusion of hyperspectral and LIDAR remote sensing data for classification of complex forest areas[J]. IEEE Transactions on Geoscience and Remote Sensing,2008,46(5):1416-1427.
[11]刘伟强,胡 静,夏德深.基于核空间的多光谱遥感图像分类方法[J]. 国土资源遥感,2002(3):44-47.
[12]杨志民,刘广利.不确定性支持向量机[M]. 北京:科学出版社,2007:57-63.
[13]罗小波,赵春晖,潘建平,等.遥感图像智能分类及其应用[M].北京:电子工业出版社,2011:122-178.
[14]杜培军,谭琨,夏俊士.高光谱遥感影像分类与支持向量机应用研究[M].北京:科学出版社,2012:89-115.
[15]LI J,BIOUCAS-DIAS J M,PLAZA A. Semi supervised hyper spectral image classification using soft sparse multinomial logistic regression [J]. IEEE Geosci. Remote Sens. Lett,2013,10(2):318-322.
[16]ANDRÉS SERNA,BEATRIZ MARCOTEGUI. Detection,segmentation and classification of 3D urban objects using mathematical morphology and supervised learning [J]. ISPRS Journal of Photogrammetry and Remote Sensing,2014,93:243-225.
[17]PETROPOULOS G P,KALAITZIDIS C,VADREVU K P.Support vector machines and object-based classification for obtaining land-use/cover cartography from hyperion hyper spectral imagery [J].Computers & Geosciences,2012,41:99-107.
[18]LIU Y,ZHANG B,HUANG L H,et al. A novel optimization parameters of support vector machines model for the land use/cover classification [J]. International Journal of Food,Agriculture & Environment,2012,10(2):1098-1104.
[20]HEIKKINEN V,TOKOLA T,PARKKINEN J,et al.Simulated multispectral imagery for tree species classification using support vector machines[J]. IEEE Transactions on Geoscience and Remote Sensing,2010,48(3):1355-1364.
[21]LARDEUX C,FRISON P L,TISON C,et al.Support vector machine for multifrequency SAR polarimetric data classification [J]. IEEE Transactions on Geoscience and Remote Sensing,2009,47(12):4143-4152.
[22]HUANG X,ZHANG L P. Road centre line extraction from high-resolution imagery based on multi scale structural features and support vector machines [J].International Journal of Remote Sensing,2009,30(8):1977-1987.
[23]BURGES C.A tutorial on support vector machines for pattern recognition[J]. Data Mining and Knowledge Discovery,1998,2:121-167.
[26]CORTES C,VAPNIK V. Support vector networks[J]. Machine Learning.1995,20:273-297.
[24]CRISTIANINI N,KANDOLA J,ELISSEEFF A,et al. On kernel target alignment[C]//Dietterich T G,Becker S,Ghahramani Z,Advances in Neural Information Processing Systems 14. Cambridge:MIT Press,2002:367-374.
[25]SCHOLKOPF B A J,MULLER K R. The connection between regularization operators and support vectors kernels [J]. Neural Net Works,1998,11(3):637-649.
[26]EVGENIOU T,PONTIL M,POGGIO T.Regularization net works and support vector machines[J].Advance in Computational Mathematics,2000,13:1-50.
[27]吴涛,贺汉根,贺明科.基于插值的核函数构造[J].计算机学报,2003,26(8):990-996.
[28]DONG YU-LIN,XIA ZUN-QUAN,WANG MING-ZHENG.An MPEC model for selecting optimal parameter in support vector machines[C]//The First International Symposium on Optimization and Systems Biology. Beijing:The First International Symposium on Optimization and System Biology,2007:351-357.
(责任编辑:石绍庆)
The remote sensing image classification based on fusion kernel function of support vector machine
GULNAZ Alimjan1,2,SUN Tie-li3,Hurxida1
(1.Department of Electronics and Information Engineering,Yili Normal University,Yining 835000,China;2.School of Geographical Science,Northeast Normal University,Changchun 130024,China;3.School of Computer Science and Information Technology,Northeast Normal University,Changchun 1300117,China)
In the technology of remote sensing image classification,classification methods directly affect the classification accuracy between the samples. Current research of based on support vector machine(SVM) remote sensing image classification have achieved good results,but there is no further study on the selection of kernel function. From the selection of kernel function rules set out to research and combined with the feature of remote sensing data itself,fused several kinds of kernel function is complementary,put forward a method of composite kernel function,through compared with traditional SVM method,the experimental data show that the effectiveness of the composite kernel method.
support vector machine;remote sensing data;kernel function;spectrum
1000-1832(2016)03-0060-07
2015-09-18
国家自然科学基金资助项目(61363066);新疆高校科研计划重点研究项目(XJEDU2014I043);吉林省科技发展计划项目(20120302);伊犁师范学院院级重点项目(2015YSZD04).
古丽娜孜·艾力木江(1972—),女,博士研究生,副教授,主要从事模式识别与遥感数据分类研究.
TP 391.1[学科代码]520·30
A
[DOI]10.16163/j.cnki.22-1123/n.2016.03.012

