三角函数多项式的实根分离

陈世平刘　忠

（1.四川省商贸学校-中国民航飞行学院德阳校区，四川省　德阳市　618000；2.乐山职业技术学院，四川省　乐山市　614000）

三角函数多项式的实根分离

陈世平1刘忠2

（1.四川省商贸学校-中国民航飞行学院德阳校区，四川省德阳市618000；2.乐山职业技术学院，四川省乐山市614000）

本文探索非多项式型实函数的实根分离问题，实现了分离三角函数多项式实根的“完备算法”，即可以找出一个互不相交的区间列，每一个区间包含函数一个实根，整个列表包含函数的全部实根，且每个区间长度可以小于任意指定精度.

三角函数多项式；实根分离；区间列；终止性

0　引言

实根分离是实代数的基本算法之一，不仅有很强的理论意义，也有广泛的应用前景.其经典工作都是围绕一元整系数多项式以及零维多元多项式系统展开的，已有了丰富的成果和普遍的应用，而对于非多项式型实函数，传统的方法都不适用，因为只有多项式才有GCD算法、Sylvester结式、Sturm定理、Descartes符号法则等概念和方法［1-5］.当然对非多项式型实函数的实根求解问题，也有学者在涉及，文献［6］探索和解决了一类广义多项式（指数多项式）的实根分离问题，文献［7］利用符号计算中区间算术的思想和指数函数连分数展开的技巧对算法进行了改进.有关其它非多项式型实函数方程的符号求解或精确求解此前未见报道.

本文的目标是探讨另一类广义多项式（三角函数多项式）的实根求解问题，如已知渐开线方程θ=inv（α）=tan（α）-α的θ值，需要求解α的值.迭代法是此类问题通用而有效的数值求解方案（如Matlab），但迭代法需要输入适合的初值，也不能求出所有的根或根的区间，不能判定根的总数，有很大的局限性，如何精确求出三角函数多项式的全部实根值得深入研究.文献［9-10］为解决“类似sin（x）＜x＜tan（x）的超越不等式”的机器证明问题［11］，设计并实现了一个三角函数多项式不等式机器证明的完备算法：运用Taylor展开式建立一个逼近目标函数的多项式区间套，从而将证明转化为一系列的一元多项式不等式的验证，然后借助代数不等式证明工具完成最后的工作，该算法回避了函数根的判定和求解问题.本文在该算法的基础上，实现了一个基于不等式证明的三角函数多项式实根分离算法：可以找出一个互不相交的区间列，每一个区间包含一个实根，整个列表包含三角函数多项式在（0，/2］内的全部实根，且每个区间长度可以小于任意指定精度.

1　三角函数多项式

定义1.1设f（x，x1，…，xn）是n+1元有理多项式，将变量x1，…，xn用sin（kx）、cos（kx）、tan（kx）（k为任意有理数）等三角函数替换后得到的函数称为三角函数多项式.

给定二元有理系数多项式环Q［x，y］，定义该环上一个映射：hom：f（x，y）→F（x），将变量y用tan（x/2）代替.

正切函数多项式在求导运算下封闭，显然

若无歧义，本文F（x）均表示正切函数多项式f（x，tan（x/2））.特别地，若fy′（x，y）恒等于0，f（x，y）是x的一元多项式，此时hom（f）=f；若fx′（x，y）恒等于0，此时f（x，y）是y的一元多项式.

定义1.3称二元多项式f（x，y）是规范的，如果fy′（x，y）与fx′（x，y）均不恒等于0.

定义1.4x0是实函数r（x）的重根，如果r（x0）=r′（x0）=0.

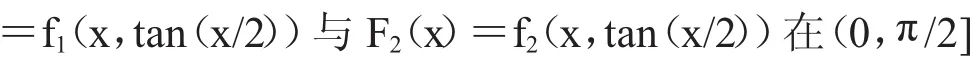
引理1.3［12］若α≠0，则α与tan（α）二者之中至少有一为超越数；

证明由引理1.3知当y0是代数数时，x0必为超越数，将f（x，y）按x降幂排列为qm（y）xm+qm-1（y）xm-1+…+q0（y），其中m＞0且qm（y）不恒等于0，因为f（x，y）不可约，所以qm（y0）、qm-1（y0）、…、q0（y0）是不能全为0的代数数，否则（y-y0）就是f（x，y）的因子，所以对任意超越数x，qm（y0）xm+qm-1（y0）xm-1+…+q0（y0）均不等于0，即F（x0）≠0.

同样的道理，当x0是代数数，则y0=tan（x0/2）为超越数，F（x0）=f（x0，y0）≠0.

引理1.5若f1（x）、f2（y）是一元有理多项式，f3（x，y）的每个因式都是二元有理规范多项式，则F1（x）=hom（f1（x））=f1（x）、F2（x）=hom（f2（y））=f2（tan（x/2））、F3（x）=hom（f3（x，y））=f3（x，tan（x/2））相互间无公根.

证明若x1是F1（x）的根，则x1是代数数，y1=tan（x1/2）必是超越数；

若x2是F2（x）=f2（tan（x/2））的根，则y2=tan（x2/2）是代数数，x2是超越数；

若x3是F3（x）的根，则必是f3（x，y）的某个不可约规范因式映射的正切函数多项式的根，由引理1.4，x3和y3=tan（x3/2）都是超越数；

所以F1（x）、F2（x）、F3（x）相互间均无公根.

由引理1.1和1.2以及1.5可以得出推论1.1.

推论1.1若（fx，y）为无重因子的二元有理多项式，则F（x）=hom（（fx，y））在（0，/2］内无重根.

引理1.6［10］若（fx，y）为二元有理多项式，则F（x）=hom（（fx，y））在（0，/2］内最多有有限个不同的根.

用f+和f-分别表示多项式f（x，y）展开式的正项和负项，显然f=f++f-，且下面的引理成立：

引理1.7假设多项式T1（y）＞0，T2（y）＞0且T1（y）＜x＜T2（y），则

f+（T1（y），y）+f-（T2（y），y）＜f（x，y）＜f+（T2（y），y）+f-（T1（y），y）.

为方便，我们将实函数f（x）的在0点Taylor展开式中的前n项记为taylor（f（x），n）或taylor（f，n）（x），即当n为奇数时taylor（arctan（x），n）=x-x3/3+…+x（2n-1）/（2n-1）（0＜x≦1），当n为偶数时taylor（arctan（x），n）=x-x3/3+x5/5-…-x（2n-1）/（2n-1）（0＜x≦1）.

引理1.8当0＜y≦1时，对任意自然数m，

（1）taylor（arctan（y），2m）＜arctan（y）＜taylor（arctan（y），2m-1）；

（2）taylor（arctan（y），2m）＜taylor（arctan（y），2m+2））；taylor（arctan（y），2m-1）＞taylor（arctan（y），2m+1）；

（3）当n→∞时，taylor（arctan（y），2m）→arctan（y），taylor（arctan（y），2m-1）→arctan（y）；

定义1.5对任意自然数n，定义

f（x，y）的上限多项式为T_max（n，f）=f+（2*taylor（arctan（y），2n-1）），y）+f-（2*taylor（arctan（y），2n），y）；

f（x，y）的下限多项式为T_min（n，f）=f+（2*taylor（arctan（y），2n）），y）+f-（2*taylor（arctan（y），2n-1），y）.

T_max（n，f）和T_min（n，f）是关于y的单变量多项式.

给定二元有理系数多项式环Q［x，y］，定义该环上一个映射：HOM：f（x，y）→G（y），将变量x用2*arctan（y）代替，即HOM（f（x，y））=f（2*arctan（y），y））.

G（y）与f（x，y）、F（x）有如下关系：在tan（x/2）=y或x=2*arctan（y）的条件下，F（x）=f（x，y）=G（y）.

引理1.9任意n∈N，在（0，1］上，函数T_max（n，f）、T_min（n，f）、G满足以下性质：

（1）T_max（n，f）＞G＞T_min（n，f）；

（2）T_max（n，f）＞T_max（n+1，f），T_min（n，f）＜T_min（n+1，f）；

（3）T_max（n，-f）=-T_min（n，f），T_max（n，-f）=-T_min（n，f）；

（4）当n→∞时，T_max（n，f）→G，T_min（n，f）→G.

即关于n，T_max（n，f）严格单调下降，T_min（n，f）严格单调上升，并且当y∈（0，1］时，有如下关系：T_min（1，f）（y）＜T_min（2，f）（y）＜T_min（3，f）（y）＜…＜G（y）＜…＜T_max（3，f）（y）＜T_max（2，f）（y）＜T_max（1，f）（y），也就是说有一个多项式区间套来逼近G（y）：（T_min（1，f）（y），T_max（1，f）（y））⊃（T_min（2，f）（y），T_max（2，f）（y））⊃（T_min（3，f）（y），T_max（3，f）（y））⊃………⊃｛G（y）｝，

本文在设计状态反馈控制器的基础之上，增加了轨迹追踪器环节，即讨论了补偿增益矩阵G的选取过程，使得系统状态量和参考轨迹输入量的误差趋近于零。最终通过Simulink仿真结果表明，本文设计的状态反馈控制器及轨迹追踪器达到了理想的设计效果。

引理1.10［9］任意y0∈（0，1］，G（y0）＜0当且仅当存在n0，使得T_max（n0，f）（y0）≤0.

引理1.11任意y0∈（0，1］，G（y0）＞0当且仅当存在n0，使得T_min（n0，f）（y0）≥0.

证明G（y0）＞0等价于-G（y0）＜0，当且仅当存在n0，使得T_max（n0，-f）（y0）≤0，等价于T_min（n0，f）（y0）≥0.

引理1.12［9］不等式G（y）＞0在区间（0，1］成立，当且仅当存在n0使得不等式T_min（n0，f）（y）≥0在（0，1］成立.

引理1.13不等式G（y）＞0在区间（a，b］成立（其中（a，b］⊂（0，1］），当且仅当存在n0使得不等式T_min（n0，f）（y）≥0在（a，b］成立.

证明令y=（b-a）t+a，由引理1.12得证.

推论1.2不等式G（y）＜0在区间（a，b］成立（其中（a，b］⊂（0，1］），当且仅当存在n0使得不等式-T_max（n0，f）（y）≥0在（a，b］成立.

由引理1.4可以得到：

引理1.14若f（x，y）是二元不可约规范有理多项式，则当y0和x0=2*arctan（y0）二者有一个为代数数时，G（y0）=f（x0，y0）≠0.

推论1.3若f（x，y）是有理多项式，且每个因式都是规范的，则当y0和x0=2*arctan（y0）二者有一个为代数数时，G（y0）=f（x0，y0）≠0.

证明若G（y0）=f（x0，y0）=0，则必然存在f（x，y）的某个不可约且规范的因式f0（x，y）满足f0（x0，y0）=0，与引理1.14矛盾.

由引理1.6还可以得出引理1.15：

引理1.15若f（x，y）为二元有理多项式，G（y）=（f（2*arctan（y），y））在（0，1］内最多有有限个不同的实根.

引理1.16若f（x，y）为无重因子二元有理多项式，G（y）=f（2*arctan（y），y）在（0，1］内无重根.

证明若y0∈（0，1］是G（x）的重根，即G（y0）=G′（y0）=0，令x0=2*arctan（y0），显然x0∈（0，/2］，则F（x0）=G（y0）=0，而F（′x0）=fx（′（x0，tan（x0/2））+（1+（tan（x0/2）2）*fy′（x，tan（x0/2））/2=fx′（x0，y0）+（1+y02）*fy′（x，y0）/2=G′（y0）*（1+y02）/2=0，即x0是F（x）的重根，与推论1.1矛盾.

引理1.17若f（x，y）为无重因子的二元有理多项式，G（y）=f（2*arctan（y），y），则在（0，1］内不等式G（y）＞0与G（y）≧0等价，G（y）＜0与G（y）≦0等价.

证明假设G（y）＞0不成立但G（y）≧0成立，即存在y0∈（0，1］，G（y0）=0，由推论1.3，y0≠1，而由引理1.12，G（y）在（0，1］内的根最多只有有限个，所以存在y0的某空心邻域，G（y）在其内不等于0，即G（y）＞0，由G（y）的可导性知G′（y0）=0，即y0是G（y）的重根，与引理1.16矛盾.

同理，G（y）＜0与G（y）≦0等价.

引理1.18若二元多项式f≠0，则G=HOM（f）≠0.

证明假设f≠0，而G=HOM（f）=0.

若fx′（x，y）≠0，将f（x，y）按x降幂排列为qm（y）xm+qm-1（y）xm-1+…+q0（y），m＞0且qm（y）不恒等于0.由tan（/4）=1和tan（2x）（1-tan（x）2）=2tan（x）知：tan（/2n）（n＞1）都是代数数，记tan（/2n）为tn，tn是代数数且arctan（tn）=/2n，而G（t）n=qm（t）n（/2n-）1m+qm-（1tn）（/2n-1）m-1+…+q（0tn），对任意n（＞1），每个q（itn）均为代数数，/2n-1为超越数，所以如果G（tn）=0，则qm（tn）=0，qm-1（tn）=0，…，q0（tn）=0.即方程qm（y）=0有无限多个不同的根，此时只有qm（y）恒等于0，与假设条件矛盾；

若fx′（x，y）=fy′（x，y）=0，即f为非0常数，此时G也等于该常数，即G≠0；若fx′（x，y）=0，fy′（x，y）≠0，此时f（x，y）是y的一次多项式，不妨记为p（y），此时G=HOM（p）=p，即G≠0，与假设条件矛盾.

引理成立.

由引理1.18知映射HOM是一一的，显然也是Q［x，y］到G上的满射，所以HOM存在逆映射HOM-1，并且f=HOM-1（HOM（f）），G=HOM（HOM-1（G））.

在以上讨论的基础上，我们设计了判断实函数G（y）=f（2*arctan（y），y）在区间（a，b］上与0的大小关系的完备算法：

算法1.1 prove_arctan_interval

输入：①反正切函数多项式G（y）；②区间（a，b］⊂（0，1］；

输出：1表示G（y）在区间（a，b］内恒大于0，-1表示恒小于0，0表示G与0在（a，b］内无固定大小关系；

BEGIN

（1）n←1；

（2）f←HOM-1（G）；

计算f的上（下）限多项式T_max（n，f）、T_min（n，f）；

ⅰ）若单变量多项式不等式T_min（n，f）≥0在（a，b］内成立，则不等式G＞0成立，return 1，算法结束；

ⅱ）若单变量多项式不等式-T_max（n，f）≥0在（a，b］内成立，则不等式G＜0成立，return-1，算法结束；

ⅲ）若T_max（n，f）＞0和T_min（n，f）＜0在（a，b］内均不成立，则G与0无固定大小关系return 0，算法结束；

（3）n←n+1，转（2）.

END.

定理1.1G（y）=HOM（f（x，y）），若f（x，y）为无重因子的二元有理多项式，则算法

1.1必然终止.

证明若G（y）＞0或G（y）＜0在某区间（a，b］（其中（a，b］⊂（0，1］）成立，则由引理

1.13和推论1.2知算法终止；

若G（y）＞0和G（y）＜0均不成立，由引理1.13知G（y）≧0和G（y）≦0也均不成立，所以存在y1、y2∈（a，b］，使得G（y1）＜0，G（y2）＞0，由引理1.10和1.11知存在n1和n2，使得T_max（n1，f）（y1）≦0，T_min（n2，f）（y2）≧0，则算法在n0=max｛n1，n2｝步循环必然终止.此时G（y1）＜T_max（n0，f）（y1）≦T_max（n1，f）（y1）≦0，G（y2）＞T_min（n0，f）（y2）≧T_max（n1，f）（y1）≧0，即G（y）与0在（a，b］内无固定大小关系.

下一章的讨论还需要判定反正切函数多项式在某一有理点的正负性.

推论1.4若f（x，y）是有理多项式，则G（y）=f（2*arctan（y），y））在（0，1］内的任意一有理点的正负性可判断.

证明令f（x，y）=f1（x，y）*f2（x）*f3（y），其中f1（x，y）的每个因式都是规范的，设有理数y0∈（0，1］.

由推论1.3知G1（y0）=f1（x0，y0）≠0，由引理1.3，arctan（y0）必为超越数，从而G2（y0）=f2（x0）≠0.

若y0是一元有理多项式f3（y）的零点，则G（y0）=f3（y0）*G1（y0）*G2（y0）=0；若f3（y0）≠0，则G2（y0）≠0，由引理1.10和1.11，若G（y0）＞0则存在n0使得T_min（n0，f）（y0）≥0，若G（y0）＜0则存在n0使得T_max（n0，f）（y0）≤0，对每个自然数n，T_min（n，f）（y）和T_max（n，f）（y）都是一元有理多项式，在有理点y0的正负性可判断.

由推论1.4知下面算法可终止.

算法1.2 sign_G##判定函数G（y）=f（2*arctan（y），y））在（0，1］内的有理点的正负性

输入 有理多项式f（x，y），有理数y0∈（0，1］；

输出1（若G（y0）＞0），0（若G（y0）=0），-1（若G（y0）＜0）；

2　正切函数多项式的实根分离

本节讨论函数F（x）=（fx，tan（x/2））在区间（0，/2］内的实根分离问题，其中（fx，y）为二元有理多项式.基本步骤如下：首先分离实函数G（y）=f（2*arctan（y），y）在区间（0，1］上的实根，再将包含G（y）根的区间转化为含F（x）根的区间，同时用二分法使区间满足任意给定精度.而分离G（y）=f（2*arctan（y），y）在某区间（a，b］上的实根的基本思路是：G（y）在（a，b］上恒大于0或恒小于0，则在（a，b］上无实根；否则，若G（y）在（a，b］上单调，则有唯一实根，若G（y）在（a，b］上不单调，则用二分法分割区间，直到每个区间要么有唯一实根，要么无实根.

判定G（y）的单调性最有效的办法就是判定其导数的正负，G（y）的导数G′（y）=2*fx′（2*arctan（y），y）/（1+y2）+fy′（2*arctan（y），y），为了去掉分母我们引入伪导数的概念：

定义2.1称G′（y）*（1+y2）为反正切函数多项式G（y）的伪导数，记Ψ（G）.

反正切函数多项式的伪导数还是反正切函数多项式，并且若Ψ（G）在（0，1］内某区间（a，b］恒大于0或小于0，则G（y）在该区间单调.

由推论1.3知当f（x，y）的每个因式都规范时，（0，1］内的任意一有理点都不是G（y）的根，而下文算法2.1和2.2中所出现的区间均是以（0，1］为基础使用二分法产生，即端点为有理数，都不是G（y）的根，所以在算法中没有严格区分开区间和闭区间.

下面的算法2.1分离反正切多项式G（y）=f（2*arctan（y），y）在（a，b］上的实根.

算法2.1 myrealroot

输入 反正切函数多项式G（y），区间（a，b］⊂（0，1］；##a、b为有理数

输出 L=｛（an，bn］｝；##（an，bn］互不相交，G（y）在每个（an，bn］内有唯一实根，L包含G（y）在（a，b］的全部实根

定理2.1若f（x，y）为无重因子的二元有理多项式，且每个因式每个因式都规范，则算法2.1必然终止.

证明由引理1.15和引理1.16知G（y）在（0，1］内最多只有有限个根且无重根，不妨记G（y）在（0，1］内的根为y1、y2、...、ym.令ε1为数轴上点y1、y2、...ym相互间距离的最小值的1/2，则y1、y2、...、ym的ε1邻域互不相交；y1、y2、...ym不是G（y）的重根，所以G（y）在点y1、y2、...ym的导数均不等于0，当然伪导数Ψ（G）也均不等于0，由Ψ（G）的连续性知存在ε2＞0，在y1、y2、...、ym的ε2邻域内Ψ（G）均不等于0.

记ε=min｛ε1，ε2｝，则在y1、y2、...ym的ε邻域内G（y）有唯一根且其伪导数恒大于或恒小于0.

取n0=［log2（1/ε）］+1（此处［x］表示不大于x的最大整数，以下同），则当n≧n0时，1/2n＜ε，而对每一个根yi，必然存在自然数si（0＜si≦2n），使得yi∈（（si-1）/2n，si/2n］，由推论1.3知道yi∈（（si-1）/2n，si/2n），此时（（si-1）/2n，si/2n）⊂o（yi，ε），即在区间（（si-1）/2n，si/2n）内G（y）有唯一根且其伪导数恒大于或小于0.

所以算法2.1在不超过n0层递归必然终止.

算法2.1能够输出一个互不相交的区间列，在其每个区间G（y）单调并有唯一根，且区间列包含G（y）在（0，1］内的全部根，下面还有两个问题需要解决：①转化为F（x）的根；②精度问题.

引理2.1若f（x，y）为无重因子的二元有理多项式，G（y）=f（2*arctan（y），y）在（0，1］上根的个数与F（x）=（fx，tan（x/2））在（0，/2］上根的个数相等.

设｛（an，bn］｝是算法2.1输出G（y）在（0，1］上的区间列，yn为G（y）在（an，bn］上的唯一根，则xn=2*arctan（yn）是F（x）的根，且xn∈（2*arctan（an），2*arctan（bn）］⊂（2*taylor（arctan（y），2m）（an），2*taylo（rarctan（y），2m-1）（bn）］，令un=2*taylo（rarctan（y），2m）（an），vn=2*taylo（rarctan（y），2m-1）（bn），则F（x）在区间（un，vn］内有根xn，若｛（un，vn］｝还互不相交，由引理2.1知F（x）在区间（un，vn］内有唯一根；因为｛（an，bn］｝互不相交，所以只要每一个（an，bn］对应的区间（un，vn］满足un≧2*arctan（an），vn≦2*arctan（bn）（或tan（un/2）≦an，tan（vn/2）≦bn），则｛（un，vn］｝也互不相交，由引理2.1知此时｛（un，vn］｝应包含F（x）=（fx，tan（x/2））在（0，/2］上的全部根.提高精度的方案还是选择二分法.

算法2.2 accuracy

输入：①反正切函数多项式G（y）；②区间（a，b］⊂（0，1］；③精度r；

##G（y）在（a，b］内单调且有唯一根，a、b为有理数；r＞0

输出：区间（c，d］；##①F（x）在（c，d］内有唯一根；②tan（c/2）≧a，tan（d/2）≦b；③d-c≦r

定理2.2若f（x，y）为无重因子的二元有理多项式，且每个因式每个因式都规范，r是任意固定精度，G（y）在（a，b］内单调且有唯一根，a、b为有理数，则算法2.2必然终止.

证明记算法2.2第n次循环后变量s、t、u、v、max_a、min_b的值分别为s（n）、t（n）、u（n）、v（n）、max_a（n）、min_b（n）；

令L=b-a，则在n次循环后区间（s（n），t（n）］的长度（t（n）-s（n））为L/2n，取n1=［log2（L/tan（r/4））］+1，则当n＞n1时，（t（n）-s（n））＜tan（r/4）；

设y0是G（y）在（a，b］内的根，令M=min｛y0-a，b-y0｝，由推论1.3知b≠y0，从而M≠0，再令n2=［log2（L/M）］+1，则当n＞n2时，（t（n）-s（n））＜M，此时t（n）-y0＜t（n）-s（n）＜b-y0，所以t（n）＜b，y0-s（n）＜t（n）-s（n）＜y0-a，所以s（n）＞a；

取n3=max｛n1，n2｝+1，则循环在第n3步时得到的区间（s（n3），t（n3）］满足：（1）G（y）在（s（n3），t（n3）］内单调且有唯一根；（2）a＜s（n3）＜t（n3）＜b；（3）（t（n3）-s（n3））＜tan（r/4）；

又因为当n→∞时，taylor（arctan，2n）（s（n3））→arctan（s（n3）），所以存在n4，使得当n＞n4时，arctan（s（n3））-taylor（arctan，2n）（s（n3））＜min｛r/8，（arctan（s（n3））-arctan（a））/2｝，从而arctan（s（n3））-taylor（arctan，2n）（s（n3））＜r/8（记为①式）以及2*taylor（arctan，2n）（s（n3））＞arctan（s（n3））+arctan（a））（记为②式）；

当n→∞时，taylor（arctan，2n-1）（t（n3））→arctan（t（n3）），所以存在n5，使得当n＞n5时，taylor（arctan，2n-1）（t（n3））-arctan（t（n3））＜min｛r/8，（arctan（b）-arctan（t（n3）））/2｝，从而taylor（arctan，2n-1）（t（n3））-arctan（t（n3））＜r/8（记为③式）以及2*taylor（arctan，2n-1）（t（n3））＜arctan（b）+arctan（t（n3））（记为④式）；

又因为当n→∞时，taylor（arctan，2n-1）（a）→arctan（a），所以存在n6，使得当n＞n6时，taylor（arctan，2n-1）（a）-arctan（a）＜（arctan（s（n3））-arctan（a））/2，从而2*taylor（arctan，2n-1）（a）＜arctan（s（n3））+arctan（a）；（记为⑤式）；

当n→∞时，taylor（arctan，2n）（b）→arctan（b），存在n7，使得当n＞n7时，arctan（b）-taylor（arctan，2n）（b）＜（arctan（b）-arctan（t（n3）））/2，从而2*taylor（arctan，2n）（b）＞arctan（b）+arctan（t（n3））（记为⑥式）；

取n8=max｛n3，n4，n5，n6，n7｝+1，显然s（n3）≦s（n8），t（n8）≦t（n3），

（v（n8）-u（n8））/2

=taylor（arctan，2n8-1）（t（n8））-taylor（arctan，2n8）（s（n8））

≦taylor（arctan，2n8-1）（t（n3））-taylor（arctan，2n8）（s（n3））

=（taylor（arctan，2n8-1）（t（n3））-arctan（t（n3）））+（arctan（s（n3））-taylor（arctan，2n8）（s（n3）））+（arctan（t（n3））-arctan（s（n3）））

＜r/4+（arctan（t（n3））-arctan（s（n3）））（由①和③得到）

又tan（arctan（t（n3））-arctan（s（n3）））=（t（n3）-s（n3））/（1+t（n3）*s（n3））＜（t（n3）-s（n3））＜tan（r/4），

即arctan（t（n3））-arctan（s（n3））＜r/4，所以（v（n8）-u（n8））/2＜r/2，从而v（n8）-u（n8）＜r.

又由②和⑤可以得到：

u（n8）=2*taylor（arctan，2n8）（s（n8））≧2*taylor（arctan，2n8）（s（n3））＞arctan（s（n3））+arctan（a））＞2*taylor（arctan，2n8-1）（a）=2*max_a（n8）；

由④和⑥可以得到：

v（n8）=2*taylor（arctan，2n8-1）（t（n8））≦2*taylor（arctan，2n8-1）（t（n3））＜arctan（s（n3））+arctan（b）＜2*taylor（arctan，2n8）（b）=2*min_b（n8）.

所以当算法2.1中的循环在第n8步时，变量u和v满足：（1）v（n8）-u（n8）＜r；（2）u（n8）＞2*max_a（n8），v（n8）＜2*min_b（n8），必然终止.

本节以上的讨论中假定了多项式的每个因式每个因式f（x，y）都规范，即fy′（x，y）≠0和fx′（x，y）≠0，现对这两种特殊情况加以分析：若fy′（x，y）=0，hom（f）是x的一元多项式，其求根问题可直接使用成熟的软件（如MAPLE、DISCOVER等）解决；若fx′（x，y）=0，hom（f）是y的一元多项式，针对此种情况我们设计了算法2.3来求解.

算法2.3realroot_y

输入一元有理多项式f（y），精度r；

输出L=｛（um，vm）｝；##（um，vm）互不相交，f（tan（x/2））在每个（um，vm）内有唯一实根，L包含（ftan（x/2））在（0，/2）的全部实根，每个区间长度小于r

定理2.3算法2.3可终止，且输出的区间互不相交.

证明算法2.3可终止等价于步骤（3）对L0中的每个区间（am，bm）循环可终止.

对区间（am，bm），记第n次循环后变量u、v、max_a、min_b的值分别为u（n）、v（n）、max_a（n）、min_b（n）；

因为当n→∞时，taylor（arctan，2n）（am）→arctan（am），所以存在n1当n＞n1时，arctan（am）-taylor（arctan，2n）（am）＜min｛r/8，（arctan（am）-arctan（s1））/2｝，从而2*taylor（arctan，2n）（am）＞arctan（am）+arctan（s1）（记为①式）；

因为当n→∞时，taylor（arctan，2n-1）（bm）→arctan（bm），所以存在n2当n＞n2时，taylor（arctan，2n-1）（bm）-arctan（bm）＜min｛r/8，（arctan（s2）-arctan（bm））/2｝，从而2*taylor（arctan，2n-1）（bm）＜arctan（s2）+arctan（bm）（记为②式）；

因为当n→∞时，taylor（arctan，2n-1）（s1）→arctan（s1），所以存在n3当n＞n3时，taylor（arctan，2n-1）（s1）-arctan（s1）＜（arctan（am）-arctan（s1））/2，从而2*taylor（arctan，2n-1）（s1）＜arctan（am）+arctan（s1）（记为③式）；

因为当n→∞时，taylor（arctan，2n）（s2）→arctan（s2），所以存在n4当n＞n4时，arctan（s2）-taylor（arctan，2n）（s2）＜（arctan（s2）-arctan（bm））/2，从而2*taylor（arctan，2n）（s2）＞arctan（s2）+arctan（bm）（记为④式）；

令n5=max｛n1，n2，n3，n4｝+1；

而tan（arctan（bm）-arctan（am））=（bm-am）（/1+bm*am）＜（bm-am）＜r/4，所以arctan（bm）-arctan（am）＜arctan（r/4）＜r/4；

从而（v（n5）-u（n5））/2＜r/2，v（n5）-u（n5）＜r；

由①和③，u（n5）=2*taylor（arctan，2n5）（am）＞arctan（am）+arctan（s1）＞2*taylor（arctan，2n5-1）（s1）=2*max_a（n5）；

由②和④ v（n5）=2*taylor（arctan，2n5-1）（bm）＜arctan（s2）+arctan（bm）＜2*taylor（arctan，2n5）（s2）=2*min_b（n5）.

所以循环到第n5步必然终止.

所以算法终止.

又对于输出的区间列｛（um，vm）｝，um＞2*max_a=taylor（arctan，2n-1）（sep_lst［m］）＞arctan（sep_lst［m］），而vm-1＜2*min_b=taylor（arctan，2n）（sep_lst［m］）＜arctan（sep_lst［m］），即um＞vm-1，（um-1，vm-1）与（um，vm）不相交，也就是说L中的区间按升序排列且互不相交.

定理2.3成立.

3　三角函数多项式实根分离与其应用实例

f（x，sin（x），cos（x），tan（x））（其中f（t，x，y，z）是有理四元多项式）是常见的三角函数多项式模型，本节具体实现其实根的分离.

文献［13］中的算法可将目标函数转化为f（x，tan（x/2））型正切函数多项式，对应的二元多项式f（x，y）可能是可约的，可先分解因式，去掉重因子，不妨还是记为f（x，y）.剩下的因子可以分为三部分：①只含x的因子，其乘积记为f1（x）；②只含y的因子，其乘积记为f2（y）；③规范的二元因子，其乘积记为f3（x，y）.即f（x，y）=f1（x）*f2（y）*f3（x，y）.由引理1.5知F1（x）=hom（f1（x））=f1（x）、F2（x）=hom（f2（y））=f2（tan（x/2））、F3（x）=hom（f3（x，y））=f3（x，tan（x/2））相互间无公根.

针对f1（x），可直接使用MAPLE（或其它软件，如DISCOVER）的realroot（f1（x），r）得到根的区间列L1；针对f2（y），可使用本文的算法2.3得到区间列L2；针对f3（x，y），可首先使用本文算法2.1，再调用算法2.2得到F3（x）的根的区间列L3.

在以上讨论基础上，我们用MAPLE实现了分离三角函数多项式实根的“完备”算法tria_realroot.

算法3.1 tria_realroot

输入 三角函数多项式F（x）=f（x，sin（x），cos（x），tan（x）），精度r0；##f是有理四元多项式

输出 互不相交的区间列L，每一个区间包含F（x）一个实根，整个列表包含F（x）在（0，/2］的全部实根，且区间长度可以小于r0；

定理3.1算法3.1必然终止.

证明F1（x）、F2（x）、F3（x）相互间无公根，由引理1.6，F1（x）*F2（x）*F3（x）最多有有限个根，设ε为其根相互间距离的最小值的1/2，则当精度小于ε时，L的区间必然互不相交.即算法3.1必然终止.

下面举例描述算法运行过程和效果：

求解过程如下：

（2）运行算法2.1，

算法1.2可以证明函数G（y）=16 arctan（y）y-2-2y2在（0，1］内既不恒大于0也不恒小于0；

G（y）的伪导数为12y+16 arctan（y）y2+16 arctan（y）-4y3，算法1.2可以证明该函数在（0，1］内恒大于0，所以G（y）在（0，1］内有唯一解，即算法2.1输出区间列［（0，1，1］］（前两个数值表示区间的左右端点，最后一个数为1表示函数在该区间内单调上升）；

（3）运行算法2.2，结果如下：

当m=1，［s，t］=［0，1/2］，［u，v］=［0，1］，［max_a，min_b］=［0，2/3］；

当m=2，［s，t］=［1/4，1/2］，［u，v］=［421441/860160，223/240］，［max_a，min_b］=［0，76/105］；

当m=3，［s，t］=［3/8，1/2］，［u，v］=［1186498729839/1653562408960，74783/80640］，［max_a，min_b］=［0，2578/3465］；

当m=4，［s，t］=［3/8，7/16］，［u，v］=［63178718862833823/88048891152302080，11951935082 346919849/14490331801064570880］，［max_a，min_b］=［0，33976/45045］；

当m=5，［s，t］=［3/8，13/32］［u，v］=［83585951172346396810929/116489387385624870256 640，879340483391699978597928424757/1139388406470395704577076756480］［max_a，min_b］=［0，11064338/14549535］.

若将左右端点的化简函数分别记为truncate_left（x，n）和truncate_right（x，n），其中n是整数的最大长度，则算法2.2中的两条运算u←2*taylor（arctan，2m）（s）和v←2*taylor（arctan，2m-1）（t）可以优化为u←truncate_left（2*taylor（arctan，2m）（s），n）和v←truncate_ right（2*taylor（arctan，2m-1）（t），n），这样可以保证输出的结果同样满足①v-u≦r和②tan（u/2）≧a，tan（v/2）≦b的要求.相应地，算法2.3也作类似的优化.

为描述算法3.1的运行过程和效果，我们随机产生例3：

（2）若r=1/100，整数长度为5，则输出结果为：

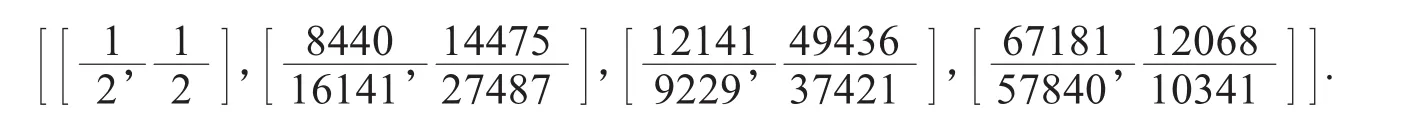
例4求反渐开线函数的值［17］：渐开线函数θ=inv（α）=tan（α）-α是机械工程中重要的函数，其中inv为渐开线involute的缩写，α是渐开线压力角，θ是渐开线展角，且α∈［0，/2］，θ∈［0，+∞），渐开线函数的逆运算称为反渐开线函数，即已知θ值，求α的值，记为α=arcinv（θ），求arcinv（θ）有许多成熟的算法，但这些算法一般都是基于迭代法，只能给出其近似值。算法3.1可以轻松计算有理数的反渐开线函数值的任意精度区间，比如当精度r=1/10000时，arcinv（1/2）

5　总结

本文在三角函数多项式不等式的自动证明算法基础上，实现了三角函数多项式实根分离完全算法：可以找出一个互不相交的区间列，每一个区间包含一个实根，整个列表包含全部实根，且区间长度可以达到任意精度.算法简单易行，十分高效，算法还可以推广到任意有理倍数三角函数f（x，tan（k1x），sin（k2x），cos（k3x））（其中k1、k2、k3为任意有理数）.特别地，算法可以轻松求解反渐开线函数，即已知渐开线方程θ=inv（α）=tan（α）-α的θ值，可以求解α的值.

在本文的讨论中，我们将F（x）=f（x，tan（x/2））的定义域限定在（0，/2］是因为arctan（y）的taylor展开式在|y|≤1时收敛.针对更一般的任意有理倍数有理三角函数多项式（fx，tan（k1x），sin（k2x），cos（k3x））（k1、k2、k3为任意有理数），根据文献［15］知函数f可以“归一”到（fx，tan（k0x））模型（其中k0为有理数），当f的定义域满足k0x（0，/4］时，算法3.1同样适用。但是，目前算法还只能求出（fx，tan（x/2））在区间（0，π/2］内的根，因为若作类似x=t+k的变量替换后多项式可能会出现超越数系数，从而关于有理三角函数多项式的性质不再成立，算法也就可能不再适用.怎么求出函数在整个实数域的全部实根或求解任意系数三角函数多项式还是值得进一步研究的课题.

［1］BUCHBERGER B，COLLINSGE.Algebraic method for geometric reasoning［J］.Annual Reviewof Computer Science，1988，3：85.

［2］WU W T.Basic principles of mechanical theorem proving in elementary geometries［J］.Journal of Systems Science and Mathematical Science，1984，4（3）：207.

［3］YANG L，ZHANG J.A practical program of automated proving for a class of geometric inequalities.proceedings ofthe automated deduction in geometry［M］.Berlin：Springer Verlag，2001：41.

［4］杨路，夏壁灿.不等式机器证明与自动发现［M］.北京：科学出版社，2008.

［5］陆征一，何碧，罗勇.多项式系统的实根分离算法及其应用［M］.北京：科学出版社，2004.

［6］ACHATZM，MCCALLUMS，WESPFENNINGV.Decidingpolynomial-exponential problems［M］.NewYork：ACMPress，215-222.

［7］徐鸣.程序验证与系统分析的若干符号计算问题［D］.上海：华东师范大学，2010.

［8］陈世平.三角函数不等式的自动证明［J］.四川大学学报（自然科学版），2013，50（3）：537-540.

［9］陈世平，刘忠.Taylor展开式与三角函数不等式的自动证明［J］.系统科学与数学，已录用

［10］陈世平，刘忠.三角函数多项式不等式的自动证明［J］.汕头大学学报（自然科学版），2015（03）：43-55.

［11］杨路，郁文生.常用基本不等式的机器证明［J］.智能系统学报，2011，6（5）：377-390.

［12］PARSHIN A N，SHAFAREVIVH I R.Number theory IV：transcendental numbers［M］.北京：科学出版社，2009.

［13］陈世平，张景中.初等不等式的可读证明的自动生成［J］.四川大学学报（工程科学版），2003，35（4）：86-93.

［14］陈世平，张景中.三角不等式的自动证明［J］.四川大学学报（自然科学版），2003，40（4）：686-690.

［15］陈世平，刘忠.一类三角形几何不等式的自动证明［J］.计算机应用研究，2012，29（5）：1732-1736.

［16］杨路，姚勇.差分代换矩阵与多项式的非负性判定［J］.系统科学与数学，2009，29（9）：1169-1177.

［17］徐克根.基于级数方法的反渐开线函数研究［J］.机械工程师，2010（6）：30-32.

Real Root Isolation of Trigonometric Function Polynomial

CHEN Shiping1，LIU Zhong2
（1.Sichuan Trade School and DeyangBranch of Civil Aviation Flight Universityof China，Deyang618000，Sichuan，China；2.Leshan Vocational TechnologyCollege，Leshan 614000，Sichuan，China）

The real root isolation for non-polynomial functions is discussed.Acomplete algorithm to isolate the real zeros of trigonometric function polynomial is presented，which can output a list of mutually disjoint intervals.Each interval contains only one zero of the generalized polynomial and the list contains all the roots of the polynomial.Furthermore，the length of each interval can be less than any given positive real number.

trigonometric function polynomial；real root isolation；interval list；termination

TP181

A

1001-4217（2016）03-0025-15

2015-09-01

陈世平（1970—），男（汉族），四川省遂宁市人，博士，研究方向：计算机代数、机器证明.E-mail：chinshiping@sina.com