基于扩展有限元的裂隙岩体锚固数值分析

王校锋

（海装上海局，上海　200083）

基于扩展有限元的裂隙岩体锚固数值分析

王校锋

（海装上海局，上海200083）

扩展有限元法是近年来提出的在标准有限元框架上解决不连续问题的一种有效数值方法.介绍了扩展有限元分析裂纹扩展的方法，应用扩展有限元法分析了裂隙岩体锚固，在裂纹扩展时引入了损伤准则.计算结果与文献给出的实验结果对比表明：扩展有限元法能较为精准地模拟裂纹的扩展，且不需要在裂纹处布置高密度的网格，裂纹扩展时也不需要网格重划分，为分析裂岩锚固提供了一种有效的模拟途径.

扩展有限元；裂隙岩体；裂纹扩展；损伤；数值模拟

大量工程实践表明：岩石边坡和大型洞室开挖等工程失稳破坏都与其内部节理或裂隙扩展贯通有关［1］.裂纹缺陷的扩展机制和锚杆对裂纹扩展的抑制机理研究一直是当今岩力学研究的难点和热点问题，大量学者运用数值方法［2-5］或试验分析［6-7］对其进行了研究.

扩展有限元法（Extended Finite Element Method，XFEM）于1999年由美国西北大学的Belytschko研究组首次提出［8-9］，在标准有限元框架下，连续区域采用标准有限元方法，不连续区域内，对有限元的位移近似函数进行修正，增加了对不连续边界的描述方法.

本文介绍了扩展有限元分析裂纹扩展的方法，并首次利用扩展有限元法对裂隙岩体锚固进行了分析，分析裂纹扩展时引入了损伤准则.

1　扩展有限元法

常规有限元方法中，位移可以表示为：

式（1）仅适用于连续介质，对于非连续介质，Belytschko等［8-9］基于单位分解的思想，将位移插值函数定义为：

式中，N为不含裂纹的常规单元节点集合；N1为被裂纹完全贯穿的单元节点集合；N2为包含裂尖的单元节点集合，如图1所示；ui、αj和bαk分别为常规单元、贯穿单元和裂尖单元节点的位移；H（x）为Heaviside函数，在裂纹面上、下侧分别取+1和-1，用来表示裂纹面位移的不连续性：

φα（x）为裂尖渐进位移场附加函数，用于反映裂尖的应力奇异性.根据线弹性断裂力学［10］，I型、II型复合裂纹尖端位移场可以表示为：

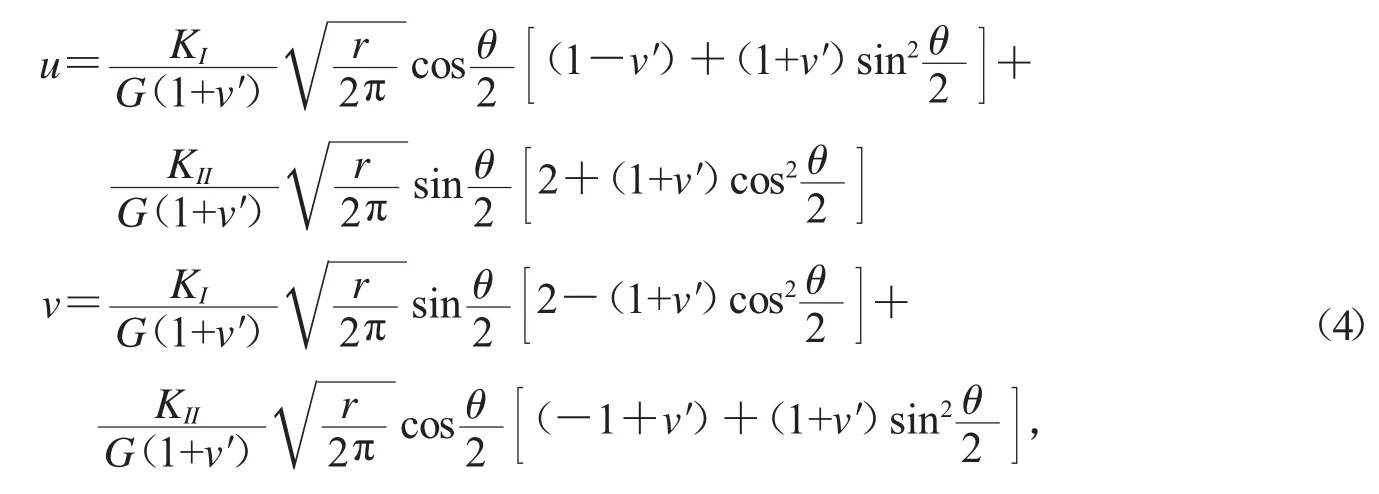
式中，

于是得到φα（x）（α=1～4）由以下基函数组成：

式中，r、θ满足以裂纹尖端为坐标原点建立的极坐标系（图1）.

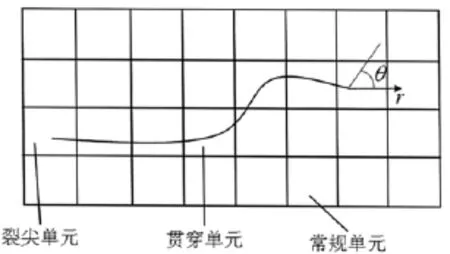
图1　含裂纹单元示意图

2　控制方程

将位移插值函数表达式（2）带入虚功原理方程，可以得到扩展有限元法的控制方程：

K为整体刚度矩阵，由单元刚度矩阵组装而成：

其中，

f为等效节点力向量：

Γt、Γu和Γc分别表示外力施加边界、位移约束边界和裂纹边界；ft和fb分别表示外力和体力（图2）.

图2　裂纹体边界条件

3　裂纹扩展及损伤准则

在裂纹扩展时引入损伤准则，当裂纹达到初始损伤准则时材料会根据损伤演化定律发生损伤.

初始损伤准侧采用最大主应力准则：

当损伤准则f大于1时，之后每一步迭代时将会发生裂纹扩展，且满足：

式中，ftol为容差.

采用双线性损伤演化定律［11］，如图3所示，当材料达到初始损伤点A时，材料开始损伤.若没有损伤演化定律，材料特性如直线OD所示为线弹性；由于损伤演化定律，材料的裂纹扩展时，材料特性将沿着直线AC方向.若达到B点时卸载，材料特性将会沿着直线BO回到O点；重新加载后材料特性会沿着折线OBC达到点C，此时材料将破坏.

图3　双线性损伤演化定律

4　裂隙岩体锚固数值模拟

裂隙岩体模型如图4（a）所示，宽为70 mm，高140 mm，厚度为20 mm，岩体中部有一穿透型裂纹，长度为42 mm，与水平轴夹角为45°；裂纹处布置3根锚杆，采用2种加锚方式.岩体的弹性模量为1.44 GPa，泊松比为0.233；锚杆的弹性模量为10.1 GPa，泊松比为0.3，直径为2.5 mm.

岩体网格划分不考虑裂纹的影响，且裂纹本身为几何特征，无需划分网格；岩体采用八节点六面体单元划分，共8 000个单元、9 471个节点；锚杆采用二节点杆单元，共60个单元、63个节点.

岩体上下受压板挤压，压板设为刚体，与压板间的摩擦系数为0.15.

图4　裂隙岩体与加锚方式示意图

图5所示为岩体在无锚固、垂直加锚和垂直裂纹加锚情况下的裂纹扩展路径示意图，可以看出三种情况下裂纹的扩展方向均平行于加载方向，与文献［12］的实验及计算结果一致，说明了本文的计算方法的正确性.

从图5的比较中可以看出，在裂纹处添加锚杆能够在一定程度上减小开裂程度.在岩体在同样的荷载作用下，无锚固岩体裂纹扩展约20 mm，垂直加锚岩体裂纹扩展约15 mm，垂直裂纹加锚岩体裂纹扩展约17 mm.

垂直加锚方式锚杆布置方向与裂纹扩展方向垂直，能较为有效地抑制裂纹扩展；对于垂直裂纹加锚方式，虽然锚杆布置方向与初始裂纹的方向垂直，但裂纹不沿着初始裂纹方向扩展，锚杆无法起到应有的效果.

从图5的裂纹扩展路径中可以看出，岩体网格不需要重划分，裂纹从单元内部扩展；且裂纹与岩体网格相互独立，在需要分析不同夹角的裂纹时，仅需调整裂纹的几何模型，不需要重新划分岩体网格.

5　结论

本文介绍了扩展有限元方法并用其对裂隙岩体锚固进行了分析，分析裂纹扩展时引入了损伤准则，得到如下结论：

（1）扩展有限元法能准确高效地模拟裂纹扩展，分析时不需要在裂纹处布置高密度网格，裂纹扩展时也无需网格重划法.

图5　不同锚固方式裂纹扩展路径与最大主应力云图

（2）开裂基体的网格和裂纹相互独立，对于不同裂纹仅需调整裂纹的几何模型，无需重新划分基体网格.

（3）裂隙岩体上下受压的情况下，开裂方向与加载方向一致，垂直加锚方式效果优于垂直裂纹加锚方式.

［1］孙静.锚杆在节理岩体中的加固作用机理和锚固效应分析及应用［D］.武汉：中国科学院武汉岩土力学研究所，2003.

［2］王忠昶，杨庆.裂隙岩体贯通及锚固止裂路径有限元分析［J］.大连理工大学学报（自然科学版），2010，50（5）：717-722.

［3］王刚，李术才，王明斌.渗透压力作用下加锚裂隙岩体围岩稳定性研究［J］.岩土力学，2009，30（9）：2843-2849.

［4］张强勇.多裂隙岩体三维加锚损伤断裂模型及其数值模拟与工程应用研究［D］.武汉：中国科学院武汉岩土力学研究所，1998.

［5］王忠昶，栾茂田，杨庆，等.裂隙岩体锚固止裂的数值模拟研究［J］.岩石力学与工程学报，2007，26（z1）：3446-3451.

［6］渠涛，韩立军，杨圣奇，等.锚固裂隙岩体力学特性试验研究［J］.河海大学学报（自然科学版），2011，39（1）：73-77.

［7］张宁.锚杆对三维裂隙岩体加固止裂效应试验研究［D］.济南：山东大学，2009.

［8］BELYTSCHKOT，BLACKT.Elastic crack growth in finite elements with minimal remeshing［J］.International Journal for Numerical Methods in Engineering，1999，45（5）：601-620.

［9］MOES N，DOLBOW J，BELYTSCHKO T.A finite element method for crack growth without remeshing［J］.International Journal for Numerical Methods in Engineering，1999，46（1）：131-150.

［10］黄志标.断裂力学［M］.广州：华南理工大学出版社，1988.

［11］CAMANHO P P，DA’VILA C G，DE MOURA M F.Numerical simulation of mixed-mode progressive delamination in composite materials［J］.J Compos Mater，2003，37（16）：1415-1438.

［12］温暖冬.裂隙岩体锚固方式优化的试验与数值模拟研究［D］.济南：山东大学，2007.

AbstractThe extended finite element method（XFEM）presented recentlyis an effective numerical method for modeling discontinuity within a standard finite element method framework.The method for crack growth analysis with XFEMis introduced.XFEMand damage criteria are used to analyze the fractured rock mass anchorage.Compared with the experimental results in the literature，the result shows the accuracy of XFEM in simulating crack growth without massive meshes in the crack tip and remeshing during the crack growth.XFEM is an effective way for simulating the fractured rock mass anchorage.

Numerical Analysis for Fractured Rock Mass Anchorage Based on Extended Finite Element Method

WANG Xiaofeng
（Shanghai MilitaryRepresentative Bureau of NavyEquipment Department，Shanghai 200083，China）

extended finite element method；fractured rock mass；crack growth；damage；numerical simulation

TU452

A

1001-4217（2016）03-0062-07

2015-10-13

王校锋（1979—），男（汉族），浙江省嵊州市人，工程师，研究方向：数值计算、控制理论与控制工程.E-mail：wangxiaofeng_sh@sina.con