湿热环境下复合材料风力机叶片气弹稳定性*
张康康 李亮† 罗杰 李映辉
(1.安徽理工大学理学院力学系, 淮南 232001) (2.西南交通大学力学与工程学院, 成都 610031)
湿热环境下复合材料风力机叶片气弹稳定性*
张康康1李亮1†罗杰1李映辉2
(1.安徽理工大学理学院力学系, 淮南232001) (2.西南交通大学力学与工程学院, 成都610031)
对湿热环境下复合材料风力机叶片气弹稳定性进行了分析. 将细长叶片简化为Euler-Bernoulli型悬臂梁,基于复合材料梁理论,在本构方程中引入湿热效应,使用Hamilton原理,建立了湿热环境下复合材料叶片弯扭(挥舞-扭转)耦合动力学方程,进而得到叶片线性自由振动特征方程,使用假设模态法求解振动特性,讨论了截面扭角、湿热效应、铺层角等因素对叶片气弹稳定性的影响,得到如下结论:(1) 扭转阻尼比非常小,易出现气弹不稳定,增加截面扭角可改善气弹稳定性;(2) 当出现气弹不稳定时,温度的升高会加剧气弹不稳定;(3) 湿度对气弹稳定性影响较小;(4) 纤维铺层角对气弹性稳定性影响显著.
风力机叶片,湿热效应,铺层角,气弹稳定性
引言
气弹稳定性是风力机叶片设计和振动控制的关键问题.目前,国内外研究多将叶片等效为各向同性的弹性体,使用截面翼型模型或连续体模型讨论设计参数、气动因素对气弹稳定性的影响.虞心田和崔尔杰[1]使用Euler 梁理论建立了准定常气动力作用下叶片挥舞-扭转耦合模型,将模型转化为等效的刚体模型,使用特征值分析方法求解气弹性问题,讨论了刚度和惯量对稳定性的影响;李本立和安玉华[2]采用Euler 梁理论建立了叶片挥舞-摆振-扭转耦合的非线性动力学方程,使用数值分析方法计算了非定常气动力下的摆振阻尼,分析了气弹稳定性;卞于中等[3]使用实验方法研究了挥舞-摆振颤振稳定性,讨论了弯曲刚度、安装角及频率、速度对稳定性的影响.
随着大型风力发电机组的开发和使用,叶片尺寸不断增大,大型风力机叶片通常由玻璃纤维、碳纤维等复合材料铺层制成,复合材料特性对叶片气弹稳定性将产生影响.Liu 和Ren[4]建立了叶片各向异性薄壁梁模型,使用经典的BEM气动力模型和Galerkin方法研究了挥舞-扭转耦合气弹稳定性;任勇生等[5]建立了叶片各向异性复合材料薄壁梁模型,使用特征值分析方法研究了入流速度比、预锥角、扭转角及纤维铺层角对叶片挥舞-摆振-扭转耦合颤振稳定性的影响;对于类似的复合材料结构,蒋宝坤等[6]使用多尺度法分析了旋转粘弹性夹层梁非线性自由振动特性,讨论了夹层厚度、转速和轮毂半径对动态特性的影响;吕书锋和张伟[7]研究了气动载荷和参数激励联合作用下的复合材料板非线性动力学行为;所得结论都可借鉴到风力机叶片振动研究.
风力发电机通常安装在山区、海上、戈壁等风资源丰富的地区,这些地区昼夜温差大、湿度高,湿热将改变复合材料叶片刚度,进而影响叶片气弹稳定性,但已有研究较少涉及湿热效应.本文将考虑湿热效应,建立湿热环境下复合材料叶片挥舞-扭转耦合动力学方程,讨论截面扭角、温度、湿度、纤维铺层角等因素对气弹稳定性的影响.
1 湿热环境下复合材料叶片动力学方程
风力机及叶片构型如图1所示[8],叶片变形有四个分量:挥舞(旋转平面外的弯曲)、摆振(旋转平面内的弯曲)、扭转、轴向拉伸.O′-xyz为随叶片旋转的体坐标系,原点在叶根截面剪切中心,x轴沿轴线方向,y轴沿摆振方向(与弦线夹角为截面扭角θ,含安装角和截面预扭角),z轴沿挥舞方向,(i j k)为坐标轴对应的单位向量.O-XYZ为风力机坐标系,原点在轮毂质心,Y轴与y轴平行,Z轴沿转轴方向,X轴由右手准则确定,(I J K)为三坐标轴对应的单位矢量.
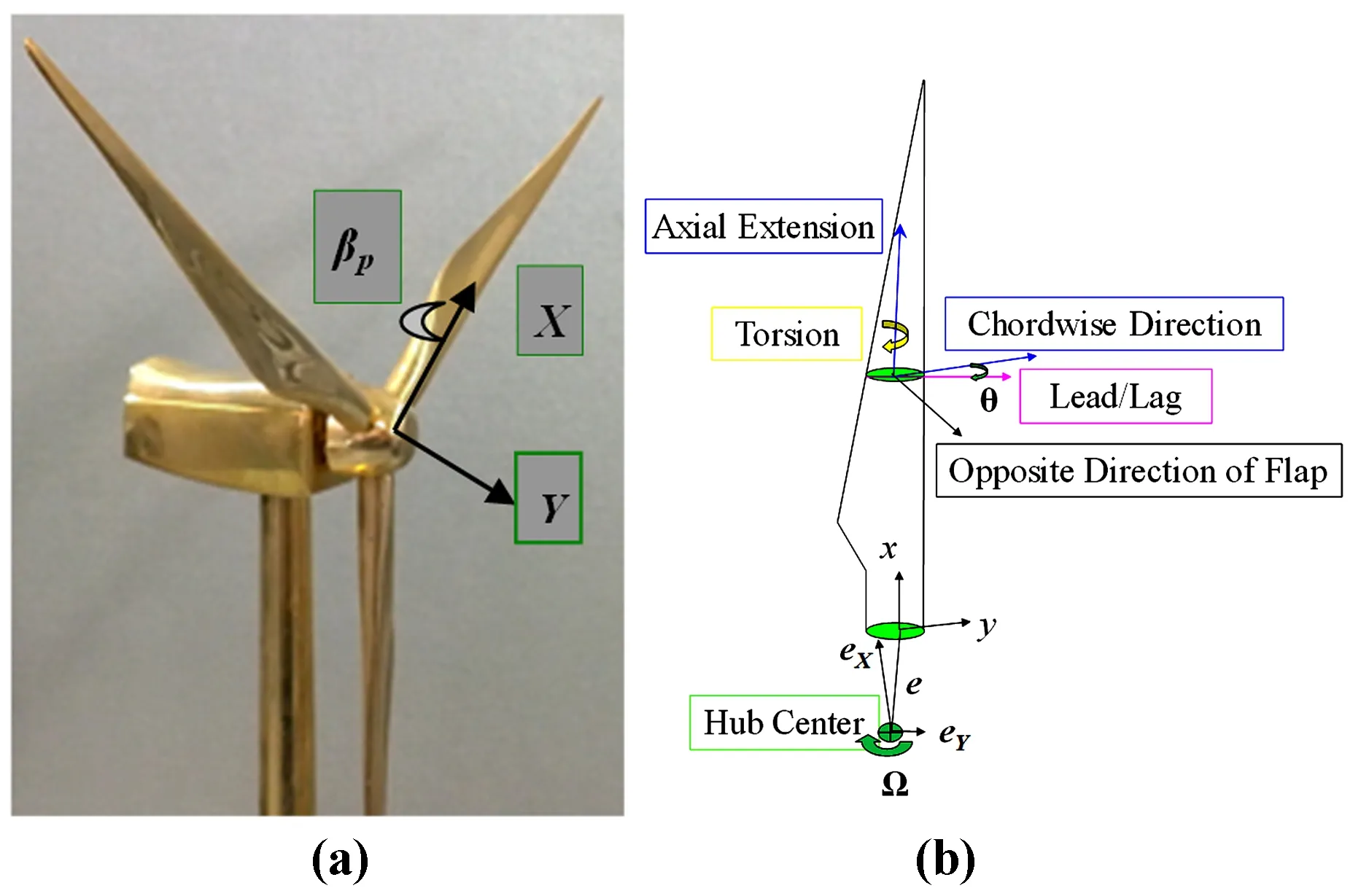
图1 (a) 风力机、(b) 叶片构型及两坐标系Fig. 1 Configuration of (a) a wind turbine and (b) a blade at two coordinate systems
研究叶片经典颤振 (挥舞-扭转耦合气弹稳定性),考虑挥舞和扭转耦合振动,为考虑离心效应,推导过程中考虑轴向拉伸,忽略小锥角βp(叶片与竖直平面的夹角),并假设叶根到轮毂的偏置量e(其沿X、Y轴的分量为eX、eY) 等于轮毂半径rh.将叶片简化为旋转复合材料悬臂梁,为方便讨论铺层角影响,本文只考虑单层梁结构.变形后,梁截面上一点P(x,y,z)在坐标系O′-xyz上的位置矢量可表示为
OP=(x+u-zw′)i+yj+(z+w)k
(1)
可得P点速度:
vP=vPXI+vPYJ+vPZK
(2)
式中各坐标分量:
(3)
u为轴向位移,w为挥舞位移,“撇”表示对空间坐标x的导数,“点”表示对时间t的导数,Ω为叶片转速.对式(3)取变分,有:
(4)
可得动能的变分:
(5)
式中,L为叶片长度,ρb为叶片密度,A为横截面积.对细长叶片可假设剪应变γxy=γxz=0,正应变
yw″sinφ-zw″cosφ
(6)
式中φ为扭转位移.湿热环境下复合材料满足如下本构关系[9-10]:
(7)
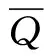
Q22sin4ψ
Q12(sin4ψ+cos4ψ)
Q22cos4ψ
(Q12-Q22+2Q66) sin3ψcosψ
(Q12-Q22+2Q66)sinψcos3ψ
Q66(sin4ψ+cos4ψ)
(8)
式中ψ为纤维铺层角,Q11=E1/(1-μ12μ21),Q22=E2/(1-μ12μ21),Q12=μ21E2/(1-μ12μ21),Q66=G12,E1、E2为材料在主方向的弹性模量,G12是剪切模量,μ12、μ21是泊松比.
可得势能的变分:
(9)
式中GJ为扭转刚度.沿z轴的外力和x轴的外力矩分别记为Fz、Mx,则外力虚功:
(10)
根据广义Hamilton原理[11]
(11)
可得叶片挥舞-扭转耦合振动线性控制方程:
(12)
(13)
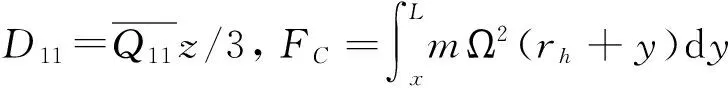
α1、α2分别表示纤维方向和垂直纤维方向的热膨胀系数,β1、β2分别表示纤维方向和垂直纤维方向的湿膨胀系数,z0为梁厚度.
分析挥舞-扭转耦合振动,可忽略重力影响,气动力采用非定常气动力模型[12],其表达式:
(14)
式中ρ为空气密度,a为升力曲线斜率,c为弦长,eA为气动中心到剪切中心的偏置量,λ为入流速度比,R为旋转半径,CDO为阻力系数.
2 自由振动特性分析
考虑叶片线性自由振动,将位移分离变量:
w=γ(w)(x)eiωt,φ=γ(φ)(x)eiωt
(15)
式中γ(w)(x)、γ(φ)(x)分别表示挥舞、扭转模态函数,ω为振动频率(其实部为固有频率,虚部为阻尼系数).将式(15)代入式(12)~(13),可得叶片线性自由振动特征方程:
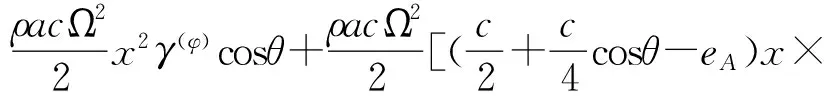
(16)
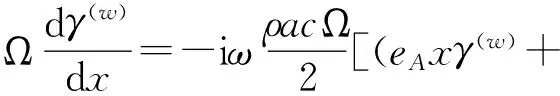
(17)
式中λs为入流速度比λ的静态部分.方程组(16)~(17)为变系数常微分方程组,其精确解无法直接求出,本文采用假设模态法[9,11,13]进行求解.选取满足几何边界条件的试函数组{φ1(w)(x),φ2(w)(x),…,φn1(w)(x)},{φ1(φ)(x),φ2(φ)(x),…,φn2(φ)(x)},n1、n2分别为挥舞、扭转试函数的个数,将模态函数表示为试函数的线性组合形式:
(18)
将式(18)代入式(16)~(17),然后在方程(16)、(17)两端分别同乘φk(μ)(μ=w、φ) 后对x从0到L积分,得到如下代数方程组:
0(n1+n2)×1
(19)
式中M和K是正定的质量和刚度阵,C是阻尼阵,T是矩阵转置,0(n1+n2)×1是(n1+n2)×1零矩阵.系数a1, …,an1,b1,…,bn2不能同时为零,所以矩阵-ω2M+iωC+K非满秩,即有
(20)
3 数值结果及讨论
本节选用文献[9,14]中的计算实例讨论截面扭角、湿热效应、铺层角对叶片气弹稳定性的影响,该模型为石墨-环氧树脂复合材料梁,表1~表3给出了不同吸湿浓度和不同温度下复合材料弹性模量以及梁几何参数,梁密度ρb=1.8×103kg/m3,转速Ω=15r/min,空气密度ρ=1.25kg/m3,轮毂半径rh=0.5m,升力曲线斜率a=2π,阻力系数CDO=0.016,轮毂处的入流速度比λs(0)=0.1,挥舞、扭转试函数分别选取为{(x/L)2,(x/L)3,(x/L)4,(x/L)5}、{sin[πx/(2L)],sin[3πx/(2L)],sin[5πx/(2L)],sin[7πx/(2L)]},这里只考虑第一阶阻尼比.
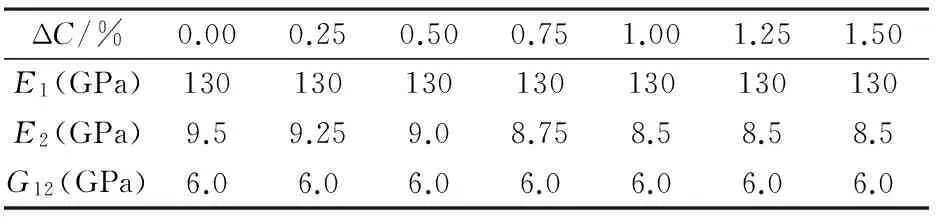
表1 不同吸湿浓度下的弹性模量:G13=G12,G23=0.5G12,
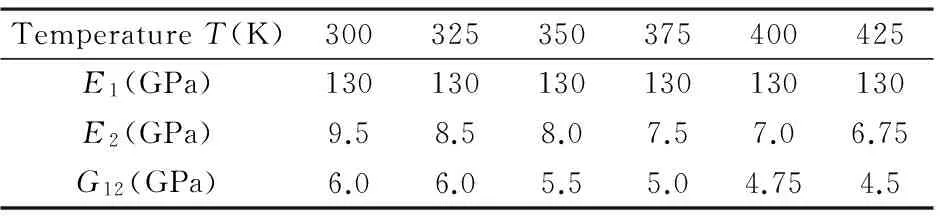
表2 不同温度下的弹性模量:G13=G12,G23=0.5G12,

表3 梁几何参数
图2给出了挥舞阻尼比ζw和扭转阻尼比ζφ随截面扭角θ的变化,其中吸湿浓度ΔC=0.00%,温度T=300K (27℃),纤维铺层角ψ=60°,θ取负号表示叶片转向与实际转向相反,θ=0°对应第一主惯性轴,θ=90°对应第二主惯性轴,结果显示:气动阻力沿挥舞方向,因此挥舞阻尼比较大,挥舞阻尼比随截面扭角的增加而减小.扭转阻尼比非常小并且为负,其值随截面扭角绝对值的增大而增大,因此增加截面扭角有利于改善气弹稳定性.
图3揭示了挥舞阻尼比ζw和扭转阻尼比ζφ随温度的变化,其中吸湿浓度ΔC=0.00%,截面扭角θ=0°,纤维铺层角ψ=45°.挥舞频率随温度升高而降低[9,14],因而挥舞阻尼比随温度升高而增大.扭转阻尼比随温度的升高而减小,因而温度升高会加剧气弹不稳定性.
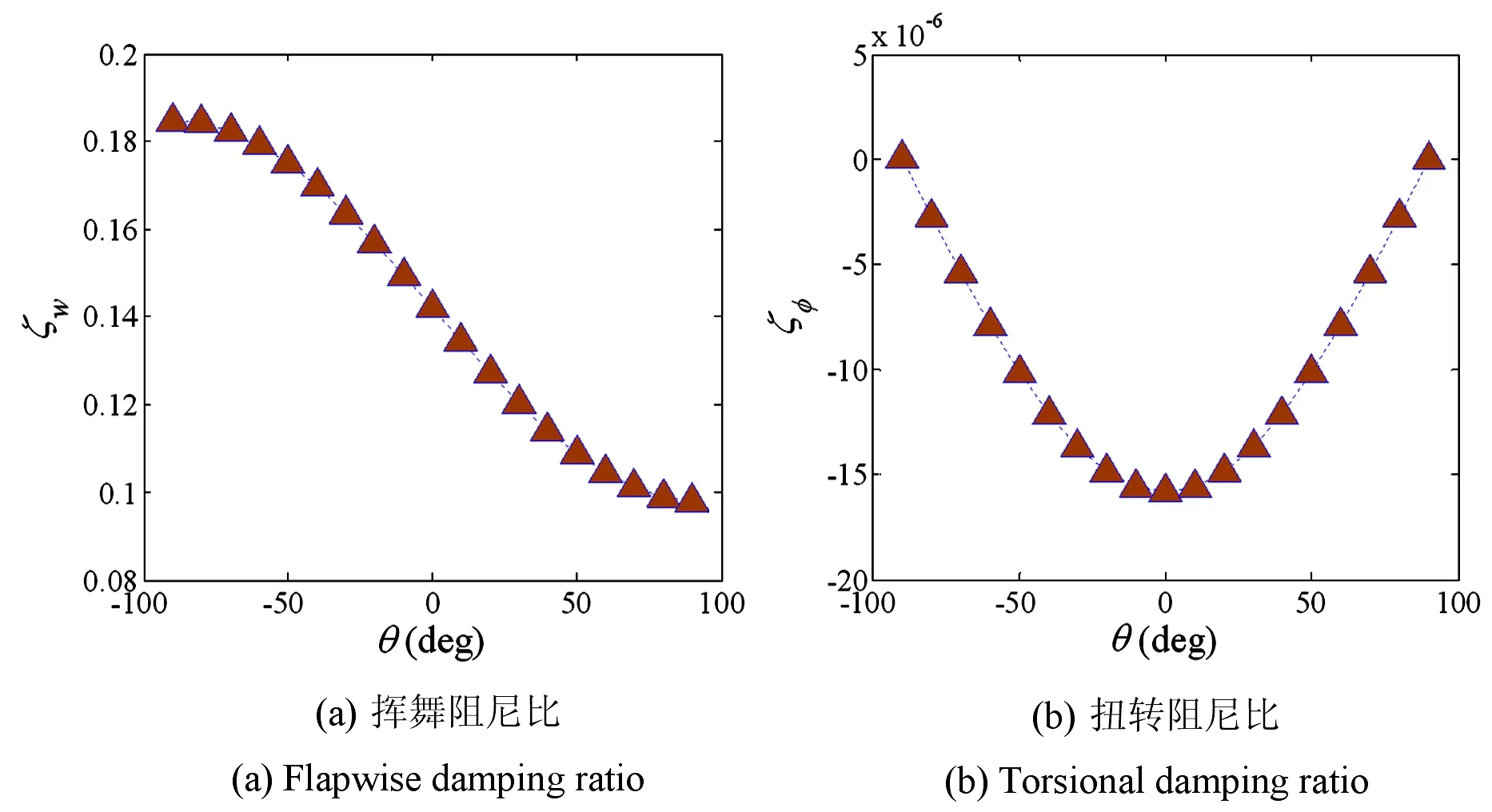
图2 阻尼比随截面扭角的变化(ΔC=0.00%,T=300K,ψ=60°)Fig. 2 Damping ratio-twist angle curves when ΔC=0.00%, T=300K, ψ=60°
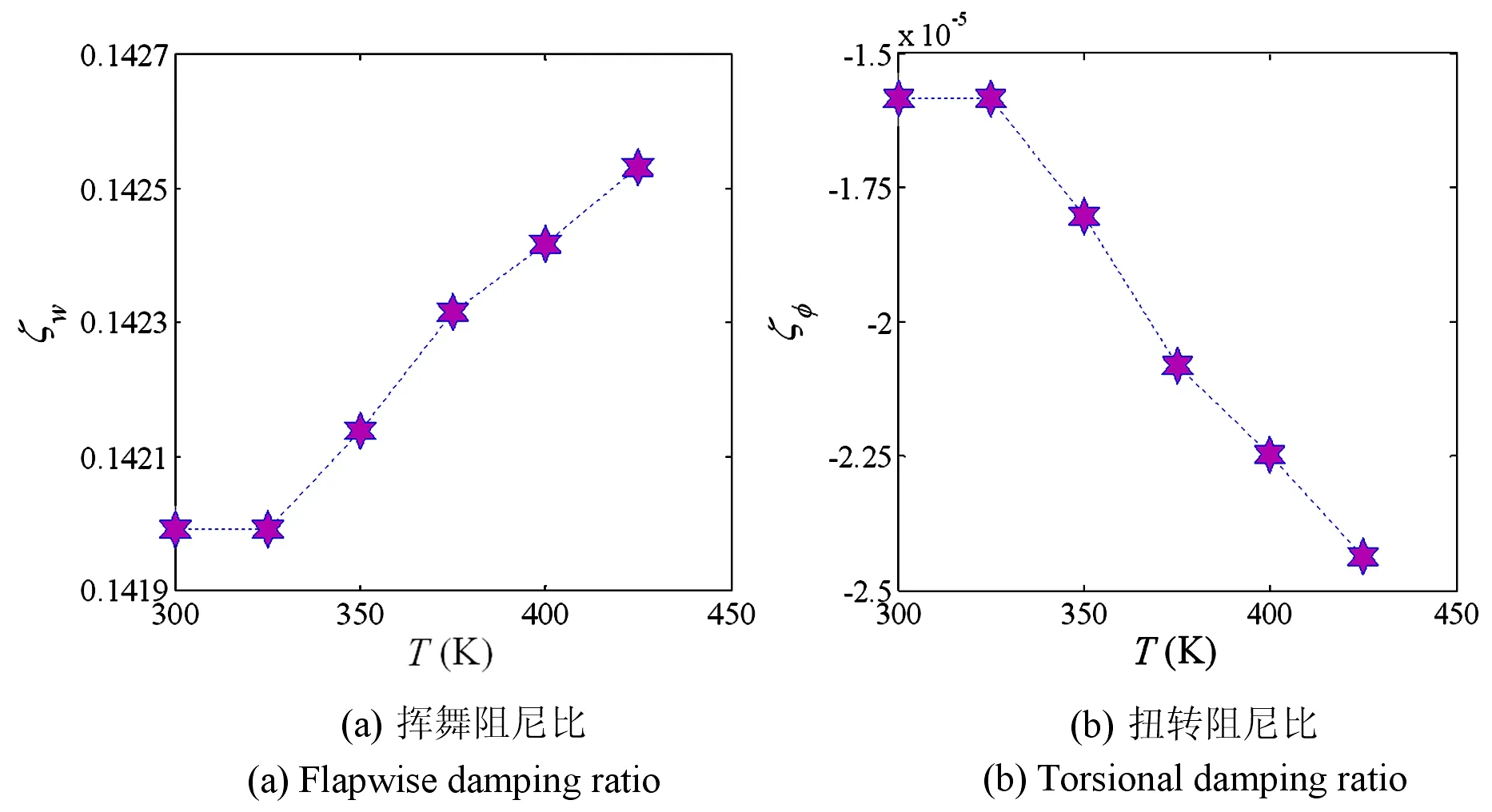
图3 阻尼比随温度的变化(ΔC=0.00%,θ=0°,ψ=45°)Fig. 3 Damping ratio-temperature curves whenΔC=0.00%, θ=0°, ψ=45°
图4给出了挥舞阻尼比ζw和扭转阻尼比ζφ随吸湿浓度的变化,其中截面扭角θ=0°,温度T=300K,纤维铺层角ψ=60°.湿度对挥舞第一阶频率影响非常小[9],对阻尼系数影响也非常小,因而阻尼比不随湿度变化.同样地,湿度对扭转频率和阻尼系数影响都很小,因而阻尼比也不随湿度变化.因此,湿度对气弹稳定性影响较小.
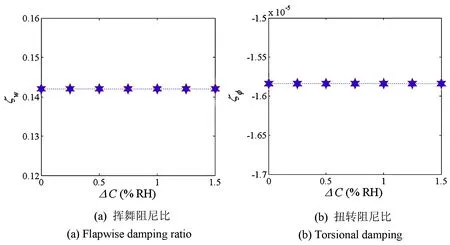
图4 阻尼比随吸湿浓度的变化(θ=0°,T=300K,ψ=60°)Fig. 4 Damping ratio-moisture concentration curves when θ=0°, T=300K, ψ=60°
图5揭示了挥舞和扭转阻尼比随纤维铺层角的变化,其中截面扭角θ=0°,温度T=301K,吸湿浓度ΔC=0.00%.结果显示,铺层角对阻尼比影响显著,两个阻尼比在0°和±60°处出现极值,当铺层角±60°时扭转阻尼比最小,此时梁振动最不稳定.
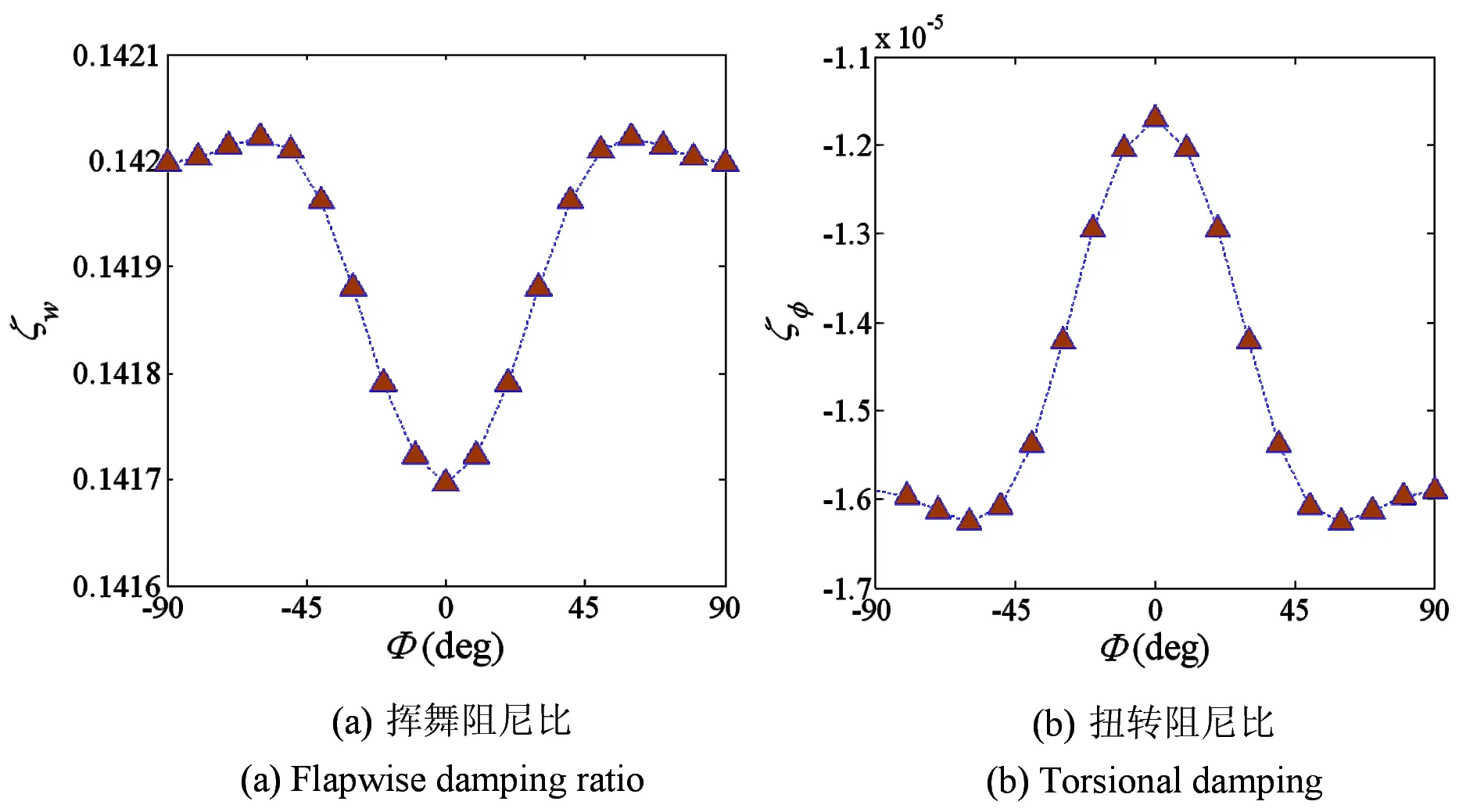
图5 阻尼比随铺层角的变化(θ=0°, T=301K,ΔC=0.00%)Fig. 5 Damping ratio-ply angle curves when θ=0°, T=301K,ΔC=0.00%
4 结论
考虑湿热效应,根据复合材料梁理论,使用Hamilton原理,建立了湿热环境下复合材料风力机叶片弯扭耦合动力学方程,基于线性自由振动方程和假设模态法,求解叶片振动特性,采用计算实例讨论了截面扭角、温度、湿度和纤维铺层角对叶片颤振稳定性的影响,得到如下结论:
1)扭转阻尼比非常小,扭转方向易出现颤振不稳定,增加截面扭角可以改善气弹稳定性;
2)扭转阻尼比随温度的升高而减小,温度升高会加剧气弹不稳定性;
3)湿度对气弹稳定性影响很小;
4)纤维铺层角对气弹性稳定性影响显著,对该模型,当铺层角±60°时叶片振动最不稳定.
1虞心田,崔尔杰. 分析水平轴风力机叶片气弹稳定性的简单方法. 太阳能学报,1990,11(1):52~59 (Yu X T, Cui E J. Simplified method for predicting the stability boundaries of a horizontal-axis wind turbine blade.ActaEnergiaeSolarisSinica, 1990,11(1):52~59 (in Chinese))
2李本立,安玉华. 风力机气动弹性稳定性的研究. 太阳能学报,1996,17(4):314~320 (Li B L, An Y H. Aeroelastic stability study for wind turbines.ActaEnergiaeSolarisSinica,1996,17(4):314~320 (in Chinese))
3卞于中,周玉,李学士. 风力机叶片气动弹性实验研究. 气动实验与测量控制,1994,8(3):29~34 (Bian Y Z, Zhou Y, Li X S. An aeroelastic experimental study of the blade of the wind turbine.AerodynamicExperimentandMeasurement&Control,1994,8(3):29~34 (in Chinese))
4LiuT R, Ren Y S. Vibration and flutter of wind turbine blade modeled as an isotro picth in-walled closed-section beam.ScienceChinaTechnologicalScience,2011,54(3):715~722
5任勇生,杜向红,杨树莲. 风力机复合材料柔性叶片的颤振分析. 振动与冲击,2011,30(9):64~69 (Ren Y S, Du X H, Yang S L. Flutter analysis of composite flexible wind turbine blades.JournalofVibrationandShock,2011,30(9):64~69 (in Chinese))
6蒋宝坤,李映辉,李亮. 旋转粘弹性夹层梁非线性自由振动特性研究. 动力学与控制学报, 2013,11(3):241~245 (Jiang B K, Li Y H, Li L. Vibration analysis of rotating viscoelastic sandwich beam.JournalofDynamicsandControl,2013,11(3):241~245 (in Chinese))
7吕书锋,张伟. 复合材料悬臂外伸板的非线性动力学建模及数值研究. 动力学与控制学报,2015,13(4):288~292 (Lu S F, Zhang W. Nonlinear analysis of deploying laminated composite cantilever plates.JournalofDynamicsandControl,2015,13(4):288~292 (in Chinese))
8Li L, Li Y H, Liu Q K, Lv H W. A mathematical model for horizontal axis wind turbine blades.AppliedMathematicalModelling,2014,38(11-12):2695~2715
9Jiang B K, Xu J, Li Y H. Flapwise vibration of a rotating beam under hygrothermal Environment.CompositeStructures,2014,117:201~211
10Christensen R M. Mechanics of composite materials. New York: John Wiley & Sons, 1979
11Meirovitch L. Computational methods in structural dynamics. Alphen aan den Rijn, The Netherlands: Sijthoff & Noordhoff, 1980
12李本立,宋宪耕,贺德馨,安玉华. 风力机结构动力学. 北京:北京航空航天大学出版社,1999 (Li B L, Song X G, He D X, An Y H. Structural dynamics of wind turbines. Beijing: Beihang University Press,1999 (in Chinese))
13李亮,吕海炜,李映辉,刘启宽. 风力机叶片挥舞振动特性分析. 力学季刊,2011,32(4):584~589 (Li L, Lv H W, Li Y H, Liu Q K. Flap vibration characteristics of wind turbine blades.ChineseQuarterlyofMechanics,2011,32(4):584~589 (in Chinese))
14Patel B P, Ganapathi M, Makhecha D P. Hygrothermal effects on the structural behaviour of thick composite laminates using higher-order theory.CompositeStructures,2002,56:25~34
*The project supported by the National Natural Science Foundation of China (11372257), Research Project Funds of Anhui University of Science and Technology, and National Training Programs of Innovation and Entrepreneurship for Undergraduates (AH201410361077, 201510361083)
† Corresponding author E-mail: LL4714052@163.com
25 June 2015,revised 23 September 2015.
AEROELASTIC STABILITY OF COMPOSITE WIND TURBINE BLADE UNDER HYDROTHERMAL ENVIRONMENT*
Zhang Kangkang1Li Liang1†Luo Jie1Li Yinghui2
(1.CollegeofScience,AnhuiUniversityofScienceandTechnology,Huainan232001,China)(2.SchoolofMechanicsandEngineering,SouthwestJiaotongUniversity,Chengdu610031,China)
The aeroelastic stability of the composite wind turbine blade under hydrothermal environment is investigated in this paper. An Euler-Bernoulli beam model is used to describe slender blade. Hydrothermal effect is introduced through constitutive equation based on composite beam theory. The governing equation of the coupled bending-torsion (flap-feather) vibration for the composite blade under hydrothermal environment is then established based on the generalized Hamiltonian principle. The characteristic equation of the blade linear free vibration is obtained from the governing equation, and the assumed-modes method is used to calculate vibration characteristics. Furthermore, the effects of twist angle of section, hydrothermal effect and ply angle on blade aeroelastic stability are discussed. The following conclusions are drawn: (1) torsion motion is prone to aeroelastic instabilitysince the damping ratio of torsion is very small, but the aeroelastic stability can be improved by increasing twist angle of section; (2) the increasing of temperature aggravates the instability when aeroelastic instability occurs; (3) the influence of moisture concentration on aeroelastic stability is very little; (4) the effect of ply angle on aeroelastic stability is large.
wind turbine blade,hydrothermal effect,ply angle,aeroelastic stability
E-mail: LL4714052@163.com
10.6052/1672-6553-2015-69
2015-06-25收到第1稿,2015-09-23收到修改稿.
*国家自然科学基金资助项目 (11372257),安徽理工大学引进博士科研启动基金资助项目,大学生创新创业资助项目(AH201410361077,201510361083)

