例谈初中学生数学直觉思维能力的培养

☉湖北省荆州市荆州区李埠中学万平

例谈初中学生数学直觉思维能力的培养

☉湖北省荆州市荆州区李埠中学万平

逻辑思维具有严格性、程序性、可靠性，但是在教育过程中，证明过程过分的严格化和程序化，学生只会看到一具具僵硬的逻辑外壳，失去学习数学的兴趣.“逻辑用于论证，直觉用于发明”.数学王子高斯曾经反复强调，他的数学发现主要来自经验，“证明只是补行的手续”.欧几里得几何学的五个公式就是基于直觉，从而建立起欧几里得几何学辉煌的大厦；阿基米德在浴室里找到了辨别王冠真假的方法.直觉思维具有简约性、创造性，对数学对象（结构及其关系）的超常把握有利于思考者从整体上驾驭问题.

徐利治教授指出：“数学直觉是可以后天培养的，实际上每个人的数学直觉也是不断提高的.”帮助学生打好扎实的基础、重视教具和学具的鼓励应用、引导学生敏锐观察、鼓励学生大胆猜想、重视数学思想方法的教学、注重解题教学等都是培养学生直觉力的高效方法.

下面的三个问题如果先让学生观察、想象或大胆猜想一下，那么对学生直觉思维的培养会有一定的帮助，对问题的解决更有效.

例1△ABC的三条边长分别是5、12、13，那么它的内切圆半径r是（）.

A.2B.5C.4D.3

分析：从整体上观察题设中的三边之长，可以发现：52+122=132，即题设△ABC为直角三角形，凭直觉可知，直角三角形内切圆的直径不可能大于或等于它的任一边之长，故必有2r＜5，选A.

例2如图1，在等腰△ABC中，AB=AC，∠A=100°，∠ABC的平分线BE交AC于点E，求BC∶（AE+BE）的值.

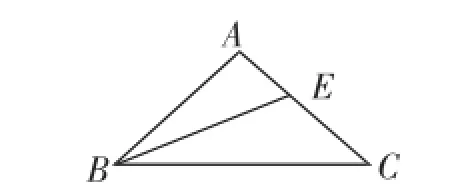
图1

分析：通过观察或测量可猜想BC=AE+BE，即猜想BC∶（AE+BE）=1.下面只需证明BC=AE+BE即可验证你的猜想，从而完成这一问题.

例3如图2，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AF平分∠CAB交CD于点E，交CB于点F，且EG∥AB交CB于点G，则CF与GB的大小关系是（）.

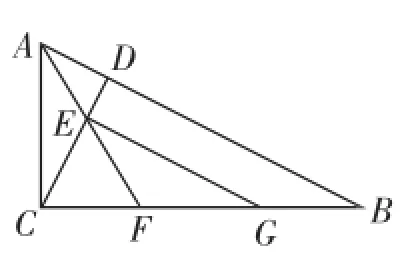
图2

A.CF＞GBB.CF=GB

C.CF＜GBD.无法确定

分析：用观察和作图法可以猜测CF=GB.下面只要证明CF=GB即可.由条件∠ACB=90°，AF平分∠CAB，想到过F点作FH⊥AB，垂足为H，连接EH，易证菱形CEHF，平行四边形EHBG，故有CF=EH=GB，从而得证.

在教学过程中，如果太侧重逻辑思维能力或计算能力和技巧的培养，反而对思维能力的整体发展有所损害.不用怀疑，学生的直觉思维能力需要得到足够重视.笔者在课堂教学中会经常碰到下列情况：一个问题刚出示，就有学生抢答，他的答案有时是对的，问其原因，回答往往令自己失望.批评他们，不但有损思考者的尊严，而且极易忽视“抢答者”思维的积极性，扼杀创造性思维于萌芽之中.鼓励这种思维，倡导猜想后的证明，比较与逻辑推理得到的结果，也许我们将培养出一位优秀的学生.

让我们再来看以下两例：

例4把一张0.2mm厚的巨大的白纸对折25下，你能猜想最后的白纸有多厚吗？会比珠穆朗玛峰的海拔高度还高吗？

例5假如把地球看作一个近似的球体，绕着赤道用一根绳子捆紧，然后把绳子放长10米（假如绳子离地球表面均等），中间的空隙能容纳下什么物体呢？

上面两例单凭学生的想象和直觉很难有正确的结果，有些同学甚至会“想入非非”、“胡思乱想”，这时教师应以科学的严密的逻辑推理予以解答，及时矫正.

有一张8cm×8cm的正方形纸片，面积是64cm2.把这张纸片按图3所示剪开，把剪出的4个小块按图4所示重新拼合，这样就得到了一个长为13cm，宽为5cm的长方形，面积是65cm2.这是可能的吗？

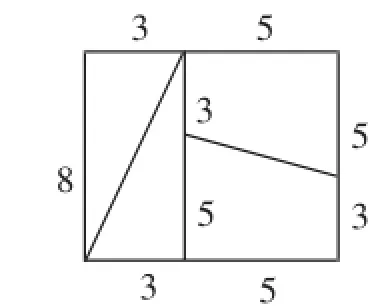
图3

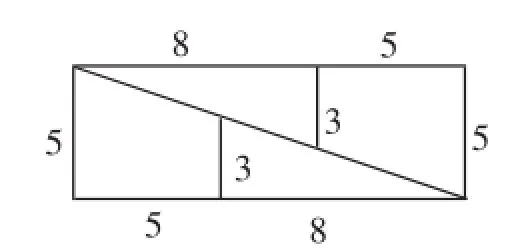
图4

这是一个直觉与逻辑不符的例子，希望学生通过学习体会到：对于数学的结论，完全凭借直觉判断是不行的，还需要通过演绎推理来验证.

一般来说，学生应当是不会相信图4中纸片的面积是65cm2，但又无法说明为什么观察的结果是错误的.进一步引导学生思考，如果观察是错误的，那么错误可能出在哪里呢？学生通过逻辑思考，可以推断只有一个可能：图4中纸片所示图形不是长方形，因此不能用长方形的面积计算公式来计算面积.然后，可以引导学生实际测量图形左上角或者右下角，发现确实不像是直角.可以告诉学生，这个想法是正确的，但最好能够给出证明，引导学生经历一个由合情推理到演绎推理的过程.

在实际教学中，可以引导学生先看图、再让学生分组将图剪开，动手操作发现矛盾（64=65？）.然后，找出理由并尝试证明，最后表达收获.

可以采用如下反证法证明，在证明过程中加深对相似图形的理解.

如图5，过点D作AC的垂线交AC于点F.假定图4中的图形是长方形，那么图形的右下角就应当是直角，则在图5中有∠1+∠3=90°.因为∠2+∠3=90°，则∠1=∠2.由相似三角形的判定定理，两个Rt△ABC与Rt△DEF相似.由相似三角形对应边成比例，应当有，这是不可能的，因此图4中的图形不可能是长方形.

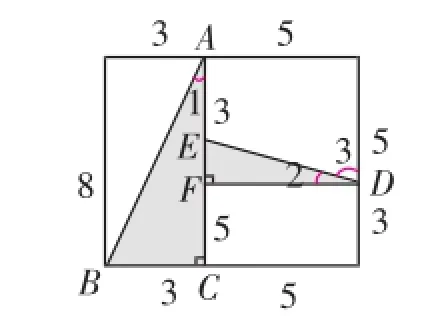
图5

教学中可以鼓励学生运用不同的方法对此问题进行解释.

直觉思维闪耀着理性思维的光辉，“含水率”时高时低也让直觉到的东西不一定可靠，但直觉的重要性显而易见.“数学的本质在于推理”，因此我们在教学过程中应该强调培养学生的逻辑思维能力和直觉思维能力的兼容.用直觉思维引导逻辑推理，通过逻辑推理检验直觉思维的正确性，帮助学生逐步养成先观察想象后证明反思的良好习惯.数学并不只是枯燥乏味的证明、推理，学习数学也可以“跟着感觉走”大胆猜测，做一个快乐的思考者.F