基于多元表征，践行变式教学——以“一次函数复习课”为例

☉浙江省绍兴市建功中学曹青

基于多元表征，践行变式教学
——以“一次函数复习课”为例

☉浙江省绍兴市建功中学曹青

我们知道，经由南京大学哲学系郑毓信教授等专家学者的推介，多元表征理论已得到不少一线教师的关注和实践.所谓的“多元表征理论”，就是强调概念表征不同方面的相互渗透与必要互补，与“单一表征理论”的“线性”、“单向性”构成了直接对照，特别是，“多元表征理论”由于突出强调了数学概念的心理表征往往包含多个不同的方面或成分，这些成分对于概念的正确理解具有重要的作用.基于该理论，我们在日常教学中可以结合变式教学，设计出很多课例，追求更有品质的教学设计，提高教学效率.本文就以近期执教的“一次函数复习课”为例，整理教学流程，并解读教学立意，提供研讨.

一、“一次函数复习”课教学流程

1.开课阶段

练习：在平面直角坐标系xOy中，一次函数y＝2x+3的图像交x轴、y轴于点A、B.

（1）直接写出点A、B的坐标；

（2）对于一次函数y＝2x+3，y随x的增大而_______；

（4）将直线y＝2x+3平移后得到直线y＝2x，请指出平移方式.

设计意图：通过这组练习让学生对一次函数的基础知识进行复习，而不是知识点填空式的开课引入.事实上，如果学生能顺利、快速地把上面4个问题都解答正确，则他们对一次函数的图像与性质、平移的规律都有很好的掌握.

2.例题讲评

例1根据下列条件确定函数y＝kx+b的解析式：

（2）直线y＝kx+b经过点（1，5）与点（-1，1）.

设计意图：这里主要复习待定系数法确定正比例函数、一次函数解析式，并且这两种函数的解析式将是后续例题研究的背景.

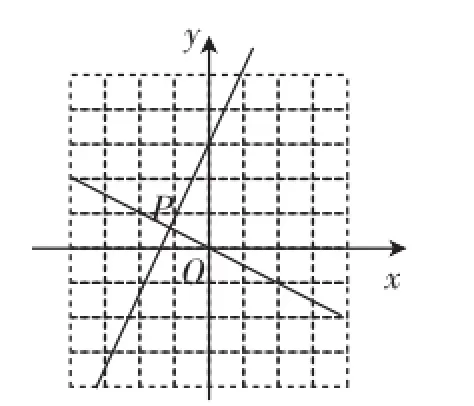
图1

（1）求出点P的坐标；

（3）当直线y＝2x+3在x轴上方时，求自变量x的取值范围；

设计意图：通过这组习题训练一次函数与方程（组）、不等式之间的数形结合的对应关系.

3.函数的“数学应用”

例3已知等腰三角形的周长为20，设腰长为x，底边长为y.

（1）写出y关于x的函数解析式；

（2）写出自变量x的取值范围；

（3）在直角坐标系xOy中，画出函数图像；

（4）设（3）中的图像上有一点P，过点P作PH⊥x轴，记△POH的面积为S，求S关于x的函数解析式.

预设追问：第（4）问有一个易错点，由于受x的取值范围的影响，点P只能在一段上取，故S关于x的函数应注意自变量的取值范围，这是不少学生容易忽略的地方.

例4【阅读材料】

同学们用“列表、描点、连线”法可以画出函数y＝|x-1|的图像，观察它的函数图像，发现图像最低点坐标为（1，0），其实根据绝对值意义就知道该函数值不可能为负，而且|x-1|还可以看成是x轴上一个动点P（x，0）到定点（1，0）的距离.

【参与解题】

（1）设M（m，0）是x轴上的一个动点，它与x轴上表示2的点的距离为s，求s关于m的函数解析式，并画出这个函数的图像.

（2）设N（0，n）是y轴上的一个动点，它与点（0，-3）的距离为s.

①求s关于n的函数解析式；

②直接写出该函数图像的最低点坐标.

预设讲评：（1）引导学生对照阅读材料分析出s＝|m-2|；并在此基础上画出图像，注意该函数图像的特殊性，若学生画成两条直线，则启发他们思考函数值是否为任意实数.

（2）类似地，先分析s＝|n+3|；再结合上一问中画图像的方法，可以得到最低点的坐标为（-3，0）.

4.小结测评

由于教学时间受限的原因，一次函数的生活应用这节课就来不及复习了.本课主要复习的是一次函数的图像与性质、解析式的确定，函数与其他数学知识的一些综合应用.

听课检测题：

（1）一次函数y＝2x-3，y随x的增大而_____.

（2）在平面直角坐标系中，直线y＝kx+b经过点（0，3）与点（-1，1），求k，b的值.

（3）在平面直角坐标系中，直线y＝2x-3在x轴下方时，求自变量x的取值范围.

（4）等腰三角形的周长为10，设腰长为a，底边长为b.试写出b关于a的函数关系式，并注明自变量a的取值范围.

（5）在平面直角坐标系中，求两条平行直线y＝2x-3与y＝2x+3之间的距离.

设计意图：前面的4个小题都是本课中提到的问题简单改编（变换了数字或字母），第（5）题则是要求学生分析本课中已提到的两条平行线之间的距离，现阶段求解需要构造直角三角形、运用勾股定理突破思路.

二、教学立意的进一步解读

1.深刻理解数学，是数学问题“多元表征”的前提

这里的深刻理解数学是指基于数学内容的关联度、贯通度、广度、深度等角度而言.如果没有教师本人对所教内容的深刻理解，很难保证所设计的教学内容能体现丰富的多元表征.我们常常见到不少教学设计或课堂教学因为教师本人缺少对前后两个问题之间的关联，以致缺少必要的点评或点睛式的讲评，使得数学教学“入宝山而空返”，留下遗憾.比如，认识到一次函数y＝2x+3的图像是直线，并熟悉点的坐标（m，2m+3）与直线y＝2x+3的关系，就可以基于它们之间多元表征的关系，设计不同的问题.

2.践行变式教学，是数学教学“多元表征”的途径

上面的课例中我们主要是践行变式教学，各个教学活动中的习题都是由教材习题变式改编，同时又注意了各个教学活动中习题之间的关联、对应，保持学生在思考过程中有一个主要的直线在心中，避免在不同的小题思考中频繁转换问题背景.这也是引导学生在一个主要问题的平台上多角度思考、探究问题.想来，这也是通过多元表征的方式追求数学教学的“多样”与“归一”.比如，从开课阶段我们就让学生保持对直线y＝2x+3的多角度研究，一直到小结阶段的课堂检测，才将这条直线变式成“一次函数y＝2x-3”，而下设的5个检测题都与这个函数有关.

3.重视对话追问，努力追求“讲活、讲懂、讲深”

我们知道，郑毓信教授一直倡导数学课堂教学的追求是：“讲活”、“讲懂”、“讲深”.讲活，在本文课例中，就是这一阶段所学的一次函数的前后知识、方法从点到面的有机联系；讲懂，就是发挥函数问题丰富的形式，基于多元表征的变式可能，通过系列变式问题多解归一，使学生真正理解有关的函数内容；讲深，就是通过精心预设对话与追问，设计一些具有挑战意味的问题，促进优秀学生“跳一跳，碰得到”.比如，我们在例3、例4与课堂检测的最后一题中都提供了类似的需要深入思考的较难问题.

三、结束语

作为文末，需要指出：无论是作为“外来”的多元表征理论，还是具有“本土”特色的变式教学理论，本身都博大精深，我们对其理论的涉猎还很初步，理解上多属盲人摸象，在这样的基础上设计的变式教学课例难免会有不足甚至错漏，诚望有识之士批评指正，打磨优化.

1.郑毓信.多元表征与概念教学［J］.小学数学教育，2011（10）.

2.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.

3.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.

4.章建跃.课堂教学要注重数学的整体性［J］.中小学数学（高中版），2013（5）.H