聚焦内容效度：函数综合题的命题追求——以两道中考模考题为例

☉江苏省常熟市浒浦学校陈玉纯

聚焦内容效度：函数综合题的命题追求
——以两道中考模考题为例

☉江苏省常熟市浒浦学校陈玉纯

函数综合题是各地中考模考的重要考题，通常会安排全卷最后两题之一，然而由于命题者个人的喜欢与旨趣，常常使得函数综合题的系列设问偏离函数的本质，甚至与函数毫无关联，转向平面几何的某个经典问题，这类考题的一个显著不足就是内容效度不够聚焦.本文选择近期关注的几例中考模考题，给出思路简述，并尝试给出变式改编与相关命题思考，提供研讨，挂一漏万，还望各位专家同行雅正.

一、模考题及思路简述

模考题1（2016年4月贵州省某地模考题）如图1，在平面直角坐标系xOy中，抛物线y=-x2+ mx+n，过点A（0，4）和C（8，0）.

（1）求m、n的值.

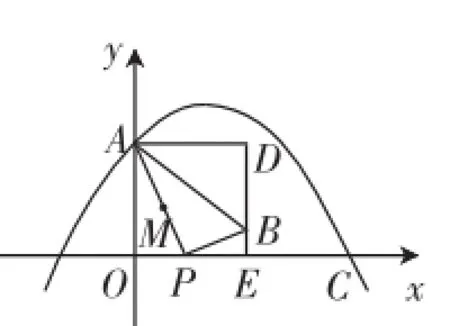
图1

（2）若P（t，0）是x轴正半轴上的一个动点，M是线段AP的中点，将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线，过点A作y轴的垂线，两直线相交于点D.

①小南同学经过分析发现：点D可以落在抛物线上.你觉得可能吗？如果可能，请求出t的值；如果不可能，请说明理由.

②当以点A、B、D为顶点的三角形与△AOP相似时，求此时t的值.

思路简述：（1）用待定系数法求出二次函数的解析式，从而得到m、n的值分别为、4.

（2）①利用△AOP∽△PEB，用含t的式子表示出点D的坐标为（t+2，4），当点D落在抛物线上时，有-（t+2）2+（t+2）+4=4，解得t=3或t=-2，再结合t＞0，故当t=3时，点D落在抛物线上.

②需要根据相似三角形的对应关系分类讨论，当点P在线段OC上和点C的右侧两种情况，也就是分别考虑当0＜t＜8时或当t＞8时两种情况，当0＜t＜8时，若△POA∽△ADB，则，即，整理得t2+16=0，此时t无解，若△POA∽△BDA，同理，解得t=-2+2.当 t＞8时，若△POA∽△ADB，则，即，

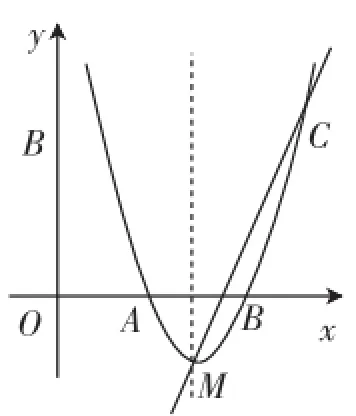
图2

模考题2（2016年4月福州市某地模考题）如图2，抛物线y=a（x-2）2-1过点C（4，3），交x轴于A、B两点（点A在点B的左侧）.

（1）求抛物线的解析式，并写出顶点M的坐标；

（2）连接OC，CM，求tan∠OCM的值；

（3）若点P在抛物线的对称轴上，连接BP，CP，BM，当∠CPB=∠PMB时，求点P的坐标.

思路突破：（1）根据待定系数法容易求出y=（x-2）2-1，顶点坐标为（2，1）.

（2）如图3，连接OM，构造直角三角形利用勾股定理（或者两点之间距离公式）求出OC、OM、CM的长，从而利用勾股定理逆定理发现△COM是直角三角形，于是可以利用正切函数的定义求出tan∠OCM的值为.

图3

（3）这一问思路较难获取，首先草图分析，分离“伪装抛物线”（如图4），进一步“目标解析”（如图5），确认∠BMP=45°，也就是要找一点P，满足∠BPC=45°，于是想到构造所谓的“一线三等角”，从而构造出图6所示的问题模式，获得重要进展.可以利用△PCQ∽△BPM分析PM的长，从而贯通思路，注意点P有两解，即（2，2+）或（2，2-√5）.

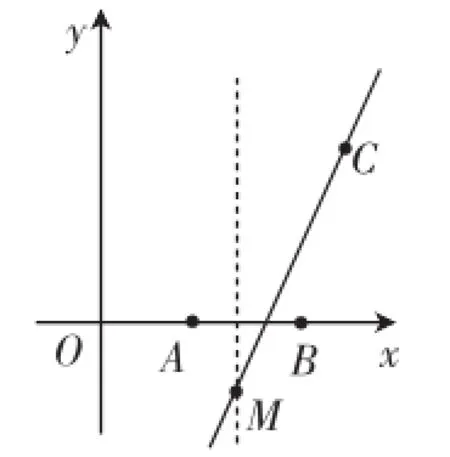
图4

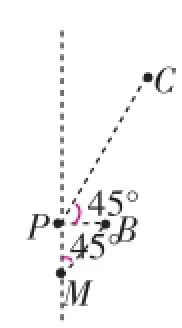
图5

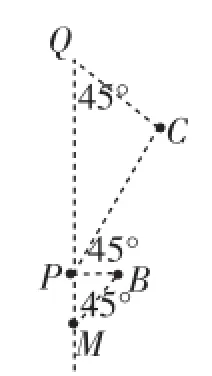
图6

二、对模考题的商榷与改编

学生是学习的主体，我们在习题命制时，应该注重学生的思维连续性，确保每个设问都并非是孤立的问题，借助于设问之间的联系，将学生原有的知识和解决数学问题的方法连贯起来，借助于问题的解决过程内化学生认知，发散学生思维，提升学生的解题能力.从上面的思路突破来看，两个模考题的最后一问基本与前面的题干没有多大关系，特别是与抛物线基本没有联系，这种让大题干提前“枯萎”的设问方式值得商榷.知易行难，以下我们对模考题2提出变式改编，提供研讨：

模考题2的第（3）问变式改编：设直线x=a分别交抛物线、x轴于点P、H.当时，求a的值.

改编意图：可以发现，我们改编的意图主要是让设问保持与题干中抛物线发生关联，而不是离开抛物线另外设问.

三、函数综合题命题的进一步思考

一个现实是，目前各级初三模考或者中考试卷中，函数为载体的（特别是二次函数）综合题出现的几率极高，然而由于初中阶段对函数包括二次函数的研究还比较局限，并没有涉及更多高中阶段中的解析几何的性质，所以很多函数综合题往往不能深入探讨函数的图像与性质，这时不少命题者选择将函数图像与几何性质相结合，生成一些人为制造的“平面直角坐标系搭台，平面几何难题构造来唱戏”的试题，由于这类试题较容易编制，也就在各类中考分类汇编、教辅资料中“流行”起来，甚至细化出很多考题分类，比如，抛物线与三角形综合题，抛物线与圆综合题，一次函数与平行四边形翻折综合题，二次函数与一次函数的综合题，以及一些动点问题等，“应试”“备考”之风在这些资料的“引领”下扎实开展.笔者根据命题经验初步思考后认为，关于函数综合题的命题，应该有如下追求：

1.函数综合题应以函数为主干，注意内容效度

从上面两个模考题来看，虽然题干中都是以抛物线为载体，但是当第（1）问明确函数关系式之后，后续的设问与抛物线基本没有多少联系，设问或考查的难点却是几何模式图形的识别与构造，这样的考题与其说是函数综合题，不如说是稍有难度的平面几何题，而且是“超标”的几何题.从命题的相关指标来看，试题的内容效度难有保证.

2.函数综合题应聚焦核心概念，注意上下关联

函数综合题如何聚焦核心概念，我们认为，应该特别体现函数本质的对应思想、增减性、数形结合等内容.此外，对于综合题来说，往往安排2～3个小问，这几个小问既要注意“递进”式设计，同时又需要注意设问的“距离”，即不同小问之间追求内在关联，从形式上看是并列式问题、互不干扰，但求解的思想方法、突破策略，却可以互为启发，这也是我们在上文提供不同模考题的变式改编的主要追求.

3.函数综合题应关注学生思维，注意经验积累

研究解答函数综合题不仅仅是为了考试多得分、得到分，反思解题过程，形成经验积累，也是数学学习中不可或缺的核心内容.解题活动的核心价值是掌握数学，解题是一种最贴近数学思维的实质性活动，是掌握数学、学会“数学地思维”的关键途径.函数综合题要关注学生数学思维的形成，要使学生学会分析，将原有的认知和解题经验迁移过来；学会思考，反思现有问题与原有经验的差异性，发散思维，避免思维定势；学会解题，在同化和顺应的过程中选择最佳的破解难题的方法和途径，在成功的体验中发展能力.唯有如此，我们的习题教学才能充分发挥学生的主观能动性，使学生的解题能力与智力、思维、能力的发展同行.

1.郑毓信.多元表征与概念教学［J］.小学数学教育，2011（10）.

2.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.

3.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.

4.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

5.【美】波利亚，著.怎样解题［M］.阎育苏，译.北京：科学出版社，1982.

6.罗增儒.中学数学解题的理论与实践［M］.南宁：广西教育出版社，2008.H