一道“阶段考题”的思路突破与讲评设计
☉江苏省张家港市梁丰初级中学蒋建东
一道“阶段考题”的思路突破与讲评设计
☉江苏省张家港市梁丰初级中学蒋建东
考题的剖析和研究是教师常规教学工作的主要组成部分,也是教师教科研的一个方向,研究的价值在于:不仅可以服务于教学质量的提升、学习效果的优化,还可以促使教师专业水平的提升,服务于素质化教育改革的发展.因此,教师在教学过程中,开展深入而有效的考题研究是非常重要的,也是非常必要的.笔者就对近期初三阶段性考试的一道压轴题进行分析和研讨.由此展开,欲以此达成抛砖引玉的效果.在最近一次初三阶段性考试中,命题老师设计了一道把关题,是抛物线与圆的综合考题,让很多考生不适应,得分率极低,本文先展示该题的思路突破,并围绕该题给出教学设计,最后对命题导向的话题给出相关思考,供研讨.
一、“阶段考题”的思路突破
(1)求b和c的值.
(2)若MN∥BC,
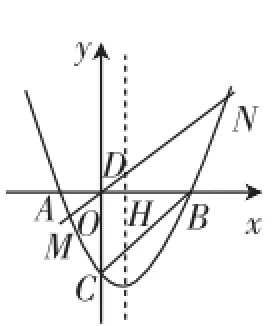
图1
①连接CD、BN,判断四边形BCDN是否为平行四边形,说明理由;
②以点D为圆心、DH长为半径画⊙D,点P、Q分别为抛物线和⊙D上的点,试求线段PQ长的最小值.
思路讲解:(1)利用待定系数法容易求出b=-1,c=-4.
(2)①首先确认直线BC的解析式为y=x-4,于是直线MN的解析式为y=x.联立抛物线的解析式y=x2-x-4和y=x-4,可解出点N的坐标,再计算出线段DN的长,与BC的长进行比较可以获得解答.
②这个问题看上去较繁难,没有思路,难以转化到初中几何中几个图形最值的模式(如两点之间线段最短;垂线段最短;轴对称最小值模式等),但是如果我们把问题稍作简化,排除干扰图形或线条的影响,就容易获得思路了,如图2,连接PD,交⊙D于Q,显然DQ是定值(⊙D的半径),故当PD最小时,PQ也就取得最小值!于是可以利用“两点间距离公式”分析PD2的最小值,而D点是定点(1,1),即有PD2=(1-x)2+,真正的障碍出现了,就是对关于x的式子的整理变形,配方得到,故PD的最小值是,相应的PQ的最小值是.

图2
解后反思:最后一问的关键是坐标平面内一个定点到抛物线上任意一点之间的距离最小问题的研究,本质上是两点间距离公式的使用,不然就需要构造直角三角形,利用勾股定理分析.也就是说,跟所谓的⊙D无甚关系,⊙D只是包装、增加解题层次而已.理解上述关键或问题的深层结构之后,我们可以根据上述考题的讲评与拓展设计出如下的教学流程,供研讨.
二、“阶段考题”的教学流程
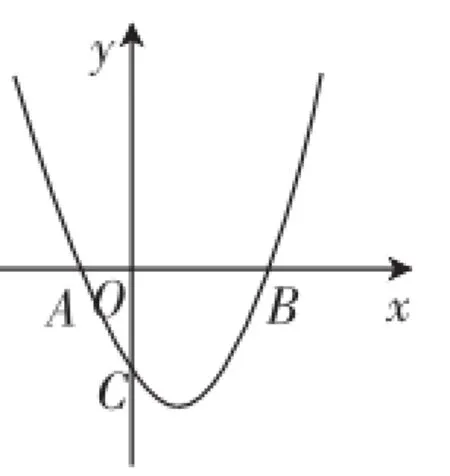
图3
问题1:能确定抛物线的解析式吗?你有哪些不同的方法?
预设互动:学生可能会使用待定系数法直接代入解析式后得出关于b、c的二元一次方程组;也可以利用“两根式”,设;还可以根据两根坐标分析出对称轴方程从而求出b.这样可体现解法路径的多样化.这样的教学不仅可以满足班级每个层面的需求,还能激发部分优生深入、多元的思考,真正达成隐性分层、多元培优的效果.
问题2:求直线BC的解析式.
预设互动:学生可能会利用待定系数法求出直线BC的解析式,也可以根据直线斜率快速分析.由此可以进一步激发学生的参与,引领学生在自我参与的过程中达成温故而知新.
问题3:将直线BC向上平移m个单位得到直线l,当直线l经过原点时,直接写出直线l的解析式.
问题4:求直线l与抛物线对称轴的交点坐标.
问题5:设直线l与抛物线在第一象限内的交点为M,求M点的坐标.
问题6:连接CD、BM,有人认为四边形BCDM是平行四边形,你觉得呢?
预设互动:问题3~6是原考题的(2)①,通过系列追问,化解求解的难点和主要步骤.这样的问题链的产生不仅可以引领学生思考、启发学生的思维,而且教师长期采用问题链的形式来进行启发和引导,也培养了学生的思维习惯,提升了学生的思维能力,无形之中可以达成授之以渔的效果.
活动2:探究点到“线”的距离.
问题7:平面直角坐标系内,有点A(2,3),点A到y轴的距离是?点A到直线x=1的距离呢?点A到直线y=x的距离呢?
预设:通过变式问题,引导学生复习并思考点到直线的距离,作出垂线段是处理此类问题的关键.而关键环节的突破因为教师的提问和学生的体验而悄然突破,达到润物细无声的效果.
问题8:平面直角坐标系中,有点D(1,1),该点到抛物线的顶点距离是多少?
问题10:平面直角坐标系中,点D(1,1),以点D为圆心、1为半径作圆,若该圆上有一点Q,抛物线上有一动点P,试分析PQ的最小值.
预设互动:启发学生回看“问题9”,与“问题10”相比有什么关联?引导学生学会分析与类比,让学生在对比中发现问题,找到突破口.
问题11:在问题10的条件下,过点P向⊙D引切线,设切点为G,当切线长PG取得最小值时,求点P的坐标.
预设互动:这个问题是“问题10”的再包装,如图4,要想PG取得最小值,只要在Rt△PDG中思考,DG是半径为定长,斜边PD取得最小值时,相应的直角边PG也取得最小值,所以问题也就转化到“问题10”.

图4
三、进一步的思考
1.思路突破重在引导学生排除干扰
我们在上面围绕该题给出系列设问的主要目的是引导学生排除干扰,逐个击破,一系列问题的价值在于设计铺垫,缩小变式距离,帮助更多学生理解难题.从命题导向上来看,原考题中的多个小问之间并列式设计,背后缺少必要的关系或递进式求解思路的启示,也加大了最后一问的求解难度.此外,从命题应该追求简洁、好懂、不超课标的目标来看,最后一问涉及繁难的数式变形、配方等,都超出了初中阶段学生应该掌握的内容,不宜出现在高危害的考试中.
2.通过变式再练提高讲评效果
根据教学经验,一般较难问题如果在课堂上讲评之后能听懂的有一部分学生,当堂听不懂的还会有一部分学生,这时如果直接追问学生是否理解,往往得到“听懂”的回复,然而事实并非如此,对于较难题、易错点,往往是貌似听懂,实则不会求解的现状,这时为了追求更好的解题教学效果,我们提倡跟进变式再练,通过变化字母、数字、图形的位置等,不破坏原题的深层结构,这样开展变式再练可以得到较好的效果.作为文末,我们围绕考题给出变式再练.
如图5,已知抛物线y=-x2+bx+c交x轴于点A(-1,0)、B(3,0),交y轴于点C,连接BC,抛物线的对称轴l分别交BC、x轴于点D、E.
(1)求b和c的值.
(2)求直线BC的函数解析式.
(3)若抛物线上有一点M(m,n),
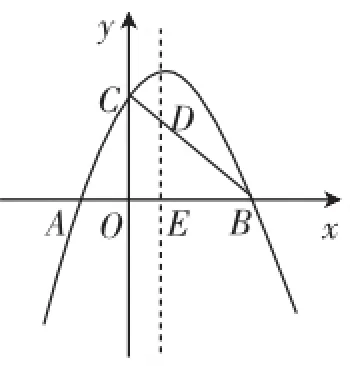
图5
①当m=-2时,求点M到原点之间的距离;
②试分析点M到原点之间距离的最小值.
③试分析点M到点D之间距离的最小值;
(4)以E为圆心、1为半径作圆,点P、Q分别为抛物线、⊙E上一动点,连接PQ,当PQ取得最小值时,求点P的坐标.
考题的研究到此其实并没有结束,教师在课后还需
要做很多的工作,比如引导学生对类似的错题进行整理和对比,对一类问题的研究进行总结和反思,在课堂的深入思维中,课后的变式训练中,训练后的反思中,不断提升学生的解题能力,不断提升学生的实际应用能力.
1.罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,2008.
2.【美】波利亚,著.怎样解题[M].阎育苏,译.北京:科学出版社,1982.
3.邓东皋,孙小礼,张祖贵,编.数学与文化[M].北京:北京大学出版社,1999.
4.钟启泉.“批判性思维”及其教学[J].全球教育展望,2002(1).Z

