预应力方套管连接胶合木梁柱节点抗弯试验

赵　艺, 何敏娟, 马人乐

(1. 同济大学 土木工程学院，上海 200092； 2. 上海绿地科技岛置业有限公司，上海 200335)



预应力方套管连接胶合木梁柱节点抗弯试验

赵艺1,2, 何敏娟1, 马人乐1

(1. 同济大学 土木工程学院，上海 200092； 2. 上海绿地科技岛置业有限公司，上海 200335)

提出在胶合木结构中采用预应力方套管螺栓连接，该连接采用高强螺栓和钢套管作为连接件.通过单调加载和往复加载下的梁柱节点抗弯试验，对比了方套管节点和传统螺栓群连接节点的破坏模式、弯矩-转角曲线、滞回曲线、强度、刚度和耗能性能.结果表明，由于摩擦阶段钢管与钢板间的摩擦力确保了初始传力，套管节点的初始转动刚度显著提升，耗能能力也得到改善.

胶合木结构; 方套管螺栓连接; 预应力; 摩擦; 刚度

螺栓连接传力明确、构造简单，在现代梁柱式木结构中应用最广.实际工程中，木框架节点承受弯矩作用，因此需要考虑节点的转动刚度.然而传统的螺栓群连接存在转动刚度过小的问题，使木框架的整体抗侧力性能较差.设计中，通常忽略螺栓连接节点有限的抗弯承载力，假定为铰接[1]；倘若要使节点达到与相连构件同等水平的刚度，节点区将会过于庞大[2].目前，针对销栓类连接的改进方法，主要有贴层加强[3-5]、自攻螺钉加强[1,6]和采用空心销[7-8]等.上述方法主要是针对节点延性的改善，因未能有效克服传统螺栓连接中孔洞间隙和初始传力的问题，对节点刚度改进有限[2].

针对上述问题，作者提出采用预应力套管螺栓连接(简称“套管节点”)提高节点的转动刚度,尤其是初始刚度.在对套管节点中采用圆套管时进行的试验研究[9]的基础上，本文在套管节点中采用方套管.通过单调加载和往复加载下梁柱节点抗弯试验，对比了方套管节点与传统螺栓群连接节点受力的不同，为其设计和应用提供参考.

1　预应力方套管螺栓连接

方套管节点由木构件、钢板、套管、高强螺栓、螺母和垫片组成，其受力原理如图1所示.组装时将套管从钢板两侧塞入木孔，组装完成后对高强螺栓施加预拉力.高强螺栓的预紧力通过螺母传给垫片，垫片从两侧对钢管产生预压力，进而钢板两侧的钢管与钢板之间也形成预压力.当外力使木构件和钢板产生相对运动趋势时，垫片、钢管、钢板之间的预压力就会在三者的接触面上产生摩擦力，并且依靠套管和木孔间的销槽承压传递外力.

受力的初始阶段，钢管和钢板之间的摩擦力可以克服钢管与螺栓或螺栓与钢板之间相对滑动的不利影响，将该阶段定义为摩擦阶段.当钢管和钢板间的摩擦力被克服，组件之间就会产生相对滑动.与传统的螺栓连接节点在受力初期需要克服螺栓和螺栓孔之间的间隙类似，将套管节点克服螺栓和套管之间间隙以及螺栓和钢板上螺栓孔之间间隙的阶段定义为滑移阶段，该阶段直到螺栓逐个与钢管内壁以及钢板上的螺栓孔壁充分接触为止.之后套管节点的受力性能与传统的螺栓连接类似，将该受力阶段定义为典型阶段.

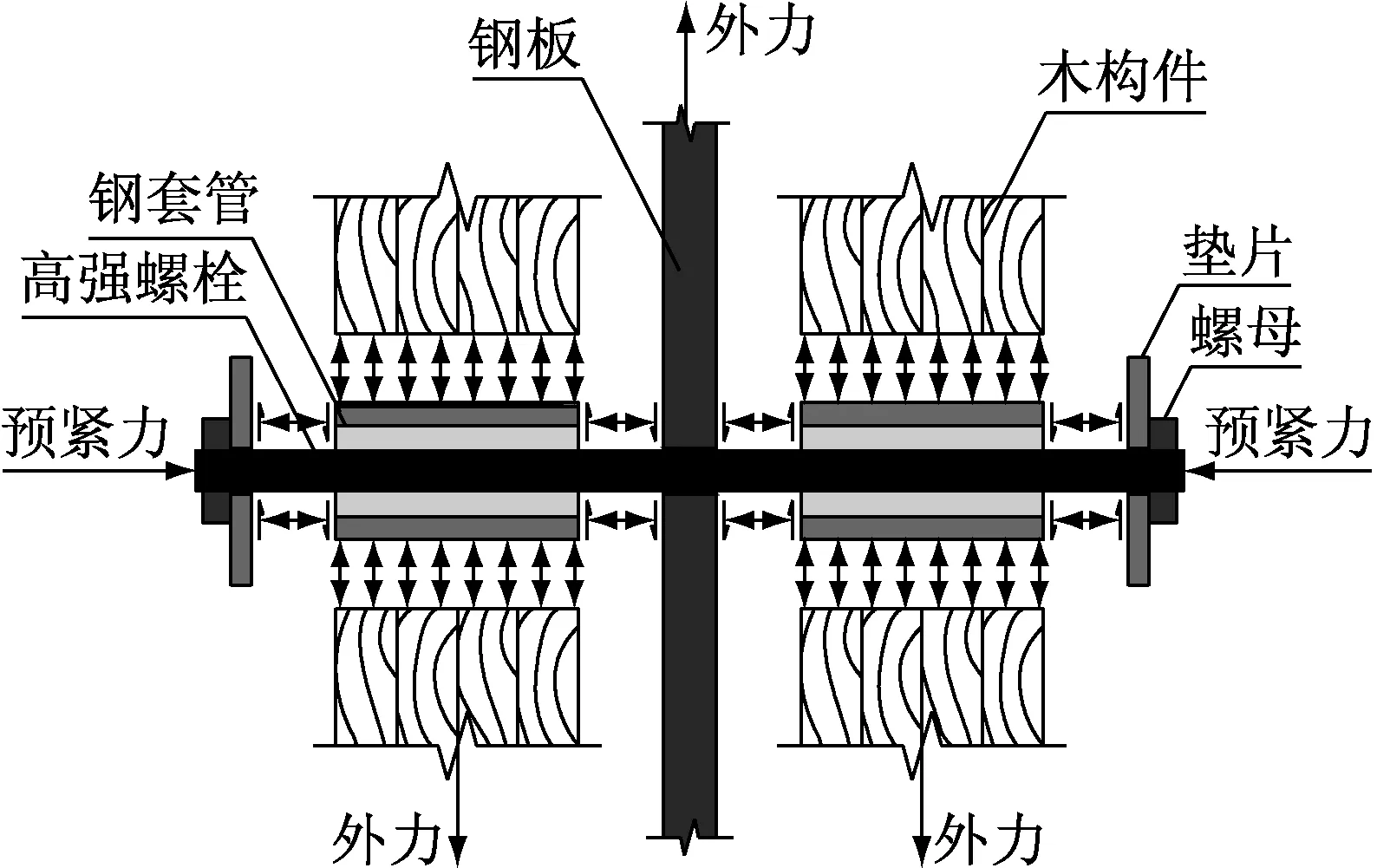
图1　方套管节点受力原理示意图

2　试验概况

试验选取常用的T型梁柱节点作为研究对象，包括2组节点，分别为方套管节点组(P组)和传统螺栓连接节点组(N组)，每组4个，2个用于单调加载(编号M)，2个用于往复加载(编号C).

2.1试验材料与试件

主要试验材料包括胶合木、钢插板、高强螺栓和钢套管等.木构件由北美云杉-松-冷杉的规格材胶合而成，按我国《木结构设计规范》[10]，该规格材的材质等级为Ⅲc.木构件的平均含水率为14.49%，平均气干密度为386.38 kg·m-3.节点尺寸如图2所示，木梁截面尺寸300 mm×150 mm，长1 000 mm；木柱截面尺寸为300 mm×200 mm，长1 200 mm；木构件开槽宽18 mm.钢板尺寸如图3所示，厚16 mm，材质等级为Q235B.

所有螺栓采用8.8级、M16的高强螺栓、中部无螺纹.P组中每个高强螺栓按照《钢结构设计规范》规定的设计预拉力值，采用脱扣式扭矩扳手施加80 kN预拉力；N组中每个螺栓按照传统螺栓连接的做法，采用普通扳手正常拧紧.方套管处的尺寸详图如图4所示，方钢管材质等级为Q345B，边长25 mm×25 mm，壁厚3 mm；用于梁、柱构件的套管长度分别为91 mm和66 mm.N组木构件上螺栓孔直径为19 mm.P组木构件上的方孔边长为26 mm，均先钻直径24 mm的圆孔，再由人工开凿方孔.为了使方套管处的木孔尽可能顺纹承压，而横纹方向不受力，因此在垂直于木纹方向,钢管与木孔的间隙采用胶水黏结;而在平行于木纹方向,钢管与木孔之间留有间隙.

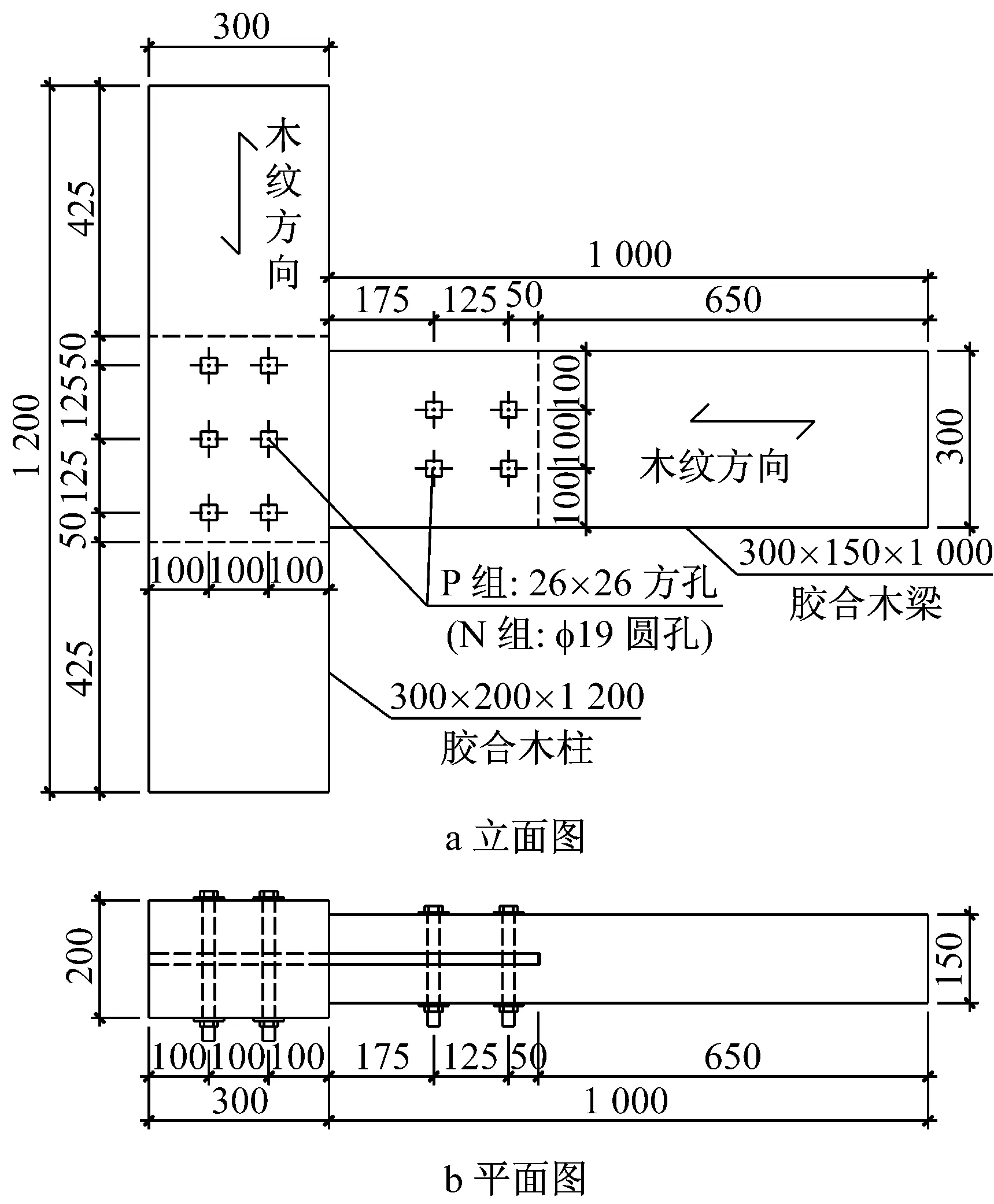
图2　节点尺寸(单位：mm)

图3　钢插板尺寸(单位：mm)

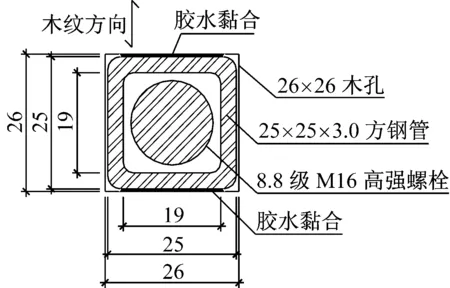
图4　方套管和木孔尺寸详图(单位：mm)

2.2试验设备与加载制度

加载装置为双通道电液伺服加载系统，水平作动器变形范围为±250 mm，能够施加的最大荷载为±300 kN.为便于加载，将木柱水平固定于加载梁上，通过作动器在梁端施加水平荷载，其加载装置和测点布置如图5所示.木梁相对木柱的转角通过设置在木梁侧面不同高度处的位移计(LVDT1～LVDT3)采集的水平位移计算得到[11-12].同理，可通过设置在钢板侧面不同高度处的位移计(LVDT4～LVDT7)采集的水平位移计算得到钢板相对木柱的转角.8号位移计(LVDT8)位于木柱端部，用于监测节点的整体位移.假定转动中心位于木柱螺栓群形心处，木梁相对木柱的弯矩M和转角θ分别按下式计算：

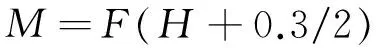
(1)

式中：F为加载头施加的水平力；H为加载头中心到木梁与木柱接触端的高差.

(2)

式中：S1，S2，S3分别为LVDT1，LVDT2和LVDT3号位移计的水平位移；0.237 5表示LVDT2和LVDT3号位移计到木梁与木柱接触端的高差为0.237 5 m.

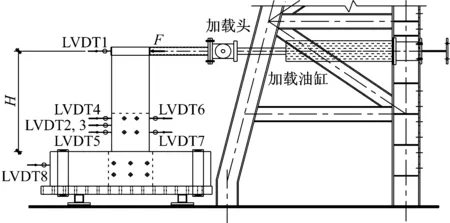
图5　加载装置与测点布置示意图

根据美国规范ASTM D1761[13]和ASTM E2126[14]，单调和往复加载均采用位移控制.对于单调加载，分为预加载和正式加载，加载速率恒为5 mm·min-1.对于往复加载，根据ASTM E2126方法C给出的CUREE(Consortium of Universities for Research in Earthquake Engineering)加载制度(图6)，其相对位移Δ为单调加载中极限位移Δfailure的60%.往复加载首先是6个位移幅值为0.05Δ的初始循环，然后是第一个主循环，其位移幅值为0.075Δ，接下来主循环位移幅值依次为0.1Δ，0.2Δ，0.3Δ，0.4Δ，0.7Δ，1.0Δ，1.5Δ，直至主循环的位移幅值达到2.0Δ，每个主循环后紧跟若干个次循环，其位移幅值为相应主循环的75%.

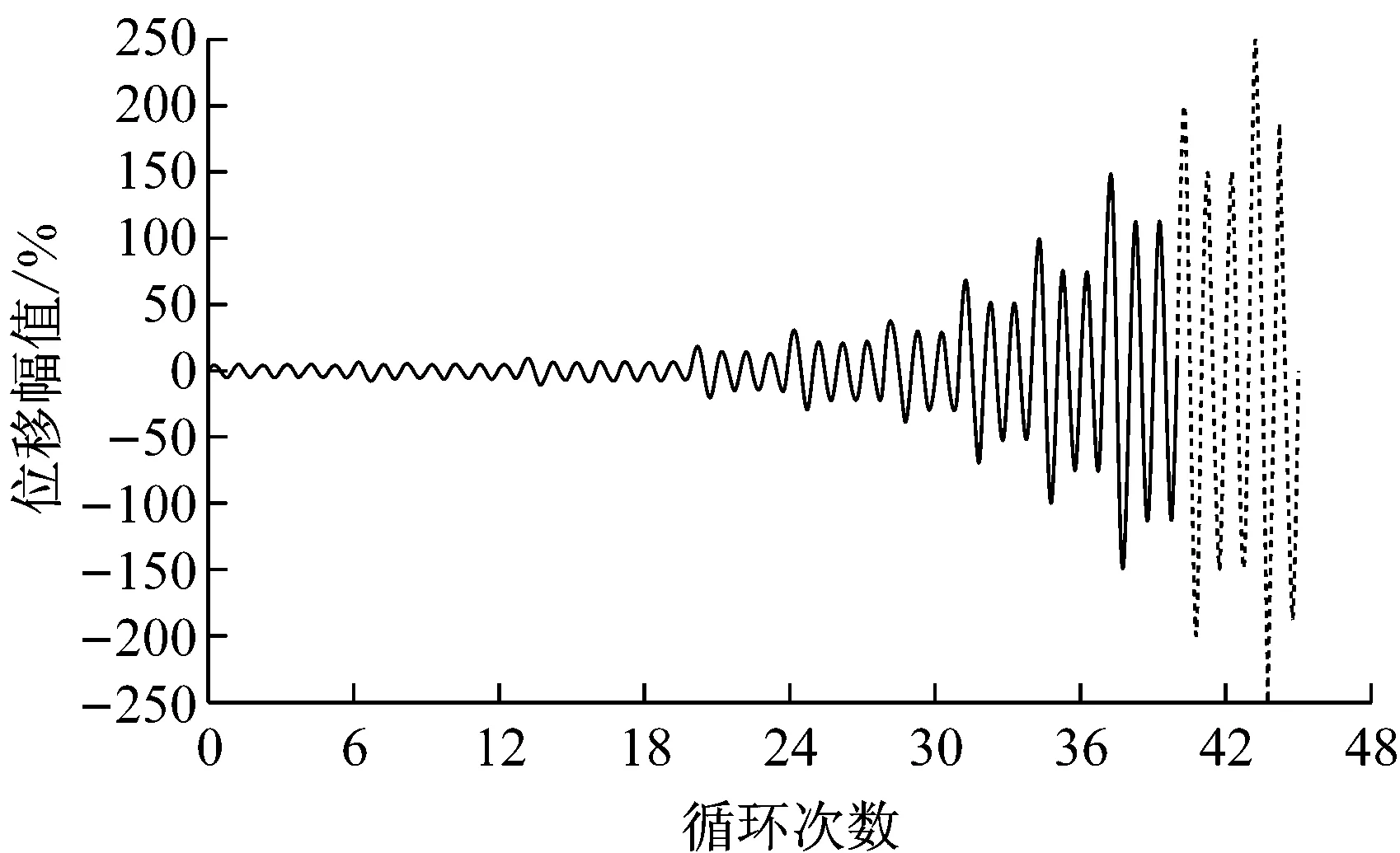
图6　CUREE加载制度

3　试验现象和破坏机理

图7和图8分别给出了两组节点单调加载和往复加载时破坏模式的对比.各组试件中的木梁均表现为刚体转动，认为其整体处于弹性范围.钢板上的螺栓孔没有视觉上的明显承压变形，可以忽略钢板对节点整体受力的影响.

aNM组bPM组

图7　单调加载破坏模式

图8往复加载破坏模式

Fig.8Failure modes in reversed cyclic loading tests

如图7a和图8a所示，传统螺栓群连接节点在弯矩荷载作用下，当螺栓与木孔处的承压力沿横纹方向的分力产生的横纹拉应力超过木材的横纹抗拉强度时，木材首先从螺栓孔附近开裂.最终木构件的主要破坏模式为顺纹劈裂，在横纹拉应力和顺纹剪应力的共同作用下，也出现了少量的列剪切破坏模式.螺栓出现了明显的弯曲变形，在与钢板的承压处出现了一个塑性铰，塑性铰以外的部分基本刚直，表现为“一铰屈服”模式.同时由于螺栓的弯曲变形，孔洞周围的木材出现了承压破坏.不过，单调加载时，木梁相对木柱翘起侧和挤压侧的螺栓弯曲程度和木孔的承压变形程度并不相同，因为在挤压侧，梁柱之间的承压传递了部分荷载，因此与梁柱承压处距离最近的螺栓和木孔变形最小(图7a).在往复荷载作用下，木梁两侧分别与木柱承压，因此木梁两侧螺栓和木孔的变形比较一致.

如图7b和图8b所示，方套管节点在弯矩荷载作用下，裂缝通常首先从木孔的角部发展为顺纹劈裂，并很快形成列剪切破坏.在摩擦阶段，加载头施加的外荷载，通过销槽承压作用，由木梁传至钢管，然后通过木梁上钢管与钢板间的摩擦传至钢板；木柱处的传力过程相反，通过木柱上钢管与钢板间的摩擦力来抵抗节点弯矩作用，然后通过钢管与木孔的销槽承压作用传至木柱，最后由木柱两端的锚固装置平衡外荷载.当方套管节点进入滑移阶段和典型阶段，螺栓逐渐与钢管内壁以及钢板上螺栓孔壁接触，螺栓与钢管以及钢管与木孔的承压传力所占比例逐渐增大，钢管与钢板间的摩擦力传递的外荷载比例逐渐减小.整个过程中，钢管在预压力作用下与钢板之间形成了摩擦力，并与木孔之间产生销槽承压作用.虽然节点构造中尽量避免了孔洞周围木材的横纹受力，但在侧向力作用下以及制造安装误差，随着变形加大，木孔附近仍会产生横纹拉应力，导致木孔角部处难免存在应力集中，并且钢管与木孔的承压面接近于平面.因此，最终木梁在顺纹剪应力和横纹拉应力的共同作用下，其主要破坏模式为列剪切破坏.另外，试验过程中发现，列剪切破坏通常首先出现在沿木纹方向的两个套管之间，因此沿木纹方向两个螺栓间距取5倍套管边长对于方套管节点而言是偏小的.方套管节点组的螺栓没有出现明显弯曲变形，且由于套管边长较大，木材较早开裂，此时木孔处的承压应力相对较小，因此孔洞周围木材的承压变形也不明显.方套管节点的木材承压强度和螺栓弯曲强度未能得到充分发挥，破坏时螺栓和钢管基本处于弹性范围，因此，与传统的螺栓连接节点相比，套管节点更易于发生脆性破坏.

由于总装机容量正在以显著的速度增长，光伏发电不可避免的在输电系统中造成重大的不确定性影响[8]。光伏发电可以描述为一个间歇性的可变发电源，因为它的生产受到天气和环境的影响，例如太阳辐射、环境温度、风速和风向[9]。在实际的系统运行中还应该考虑传统发电的影响，这对缓解不确定性问题至关重要。如果在电力系统的概率模型中不考虑发电操作的行为，则只需利用松弛总线补偿所有与光伏发电和负载有关的变化。光伏并网发电时，光伏发电的随机特性可能会对系统的有功功率平衡产生不利影响。光伏发电电源应由发电调度操作和自动发电控制（AGC）[10]进行补偿。

4　单调加载试验结果及分析

两组节点单调加载的弯矩-转角曲线如图9所示，平均弯矩-转角关系曲线的对比如图10所示.从图9b中可以看出，PM组节点的弯矩-转角曲线在0°～1.3°之间处于摩擦阶段；滑移阶段大致对应曲线上1.3°～1.8°之间的部分，该阶段节点刚度出现明显下降；当转角超过1.8°后，螺栓与钢管内壁、钢板螺栓孔壁接触，节点进入典型阶段，该阶段节点刚度又出现小幅增长.从图10可以看出，PM组节点的刚度明显大于NM组节点，但PM组节点由于木构件过早开裂,较早出现破坏.

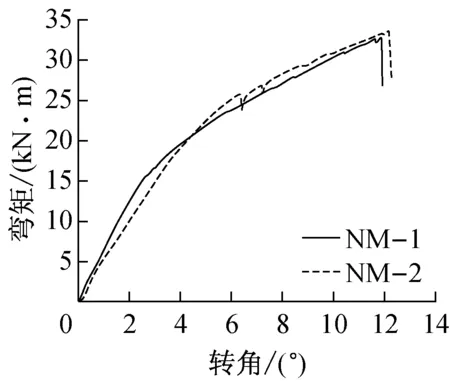
a NM组

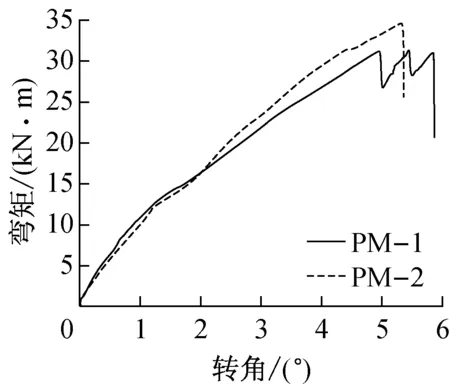
b PM组

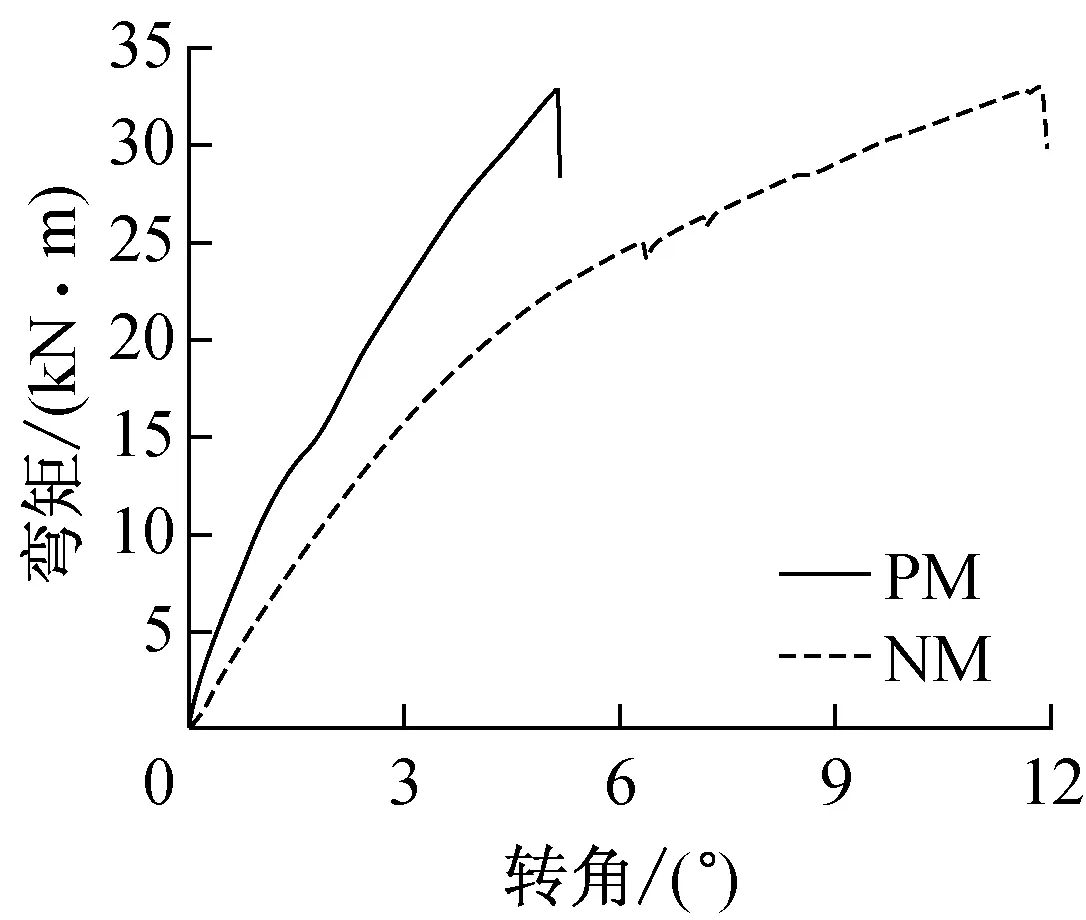
图10　两组节点单调加载平均弯矩-转角曲线对比

需要指出的是，由于制造和安装误差，套管节点组装完成后，各个螺栓处的螺栓和钢管内壁或钢板上螺栓孔壁之间可能存在随机分布的初始接触，导致当钢管与钢板间的摩擦力被克服，螺栓与钢管、钢板孔将要发生相对滑动时，整个节点滑移阶段的划分不明显.另外，变形过程中，木梁柱间的相互承压作用会传递部分荷载，导致木梁上每个螺栓处的受力大小存在差异，各个钢管与钢板不是同时发生相对滑动，从而进一步导致节点整体的阶段划分不明显.整个节点弯矩-转角曲线上体现出的滑移阶段对应的是多数套管与钢板处于滑移的阶段.

将弯矩-转角曲线的顶点对应的弯矩定义为极限弯矩Mp，相应转角为θp.将节点完全开裂时对应的转角定义为破坏转角θf，相应的弯矩为Mf.对于NM组节点，采用Y&K方法的原理(图11)计算得到其屈服点[15-16].该原理图中Ke和Kp所对应直线的斜率分别表示节点的弹性刚度和塑性刚度,屈服点对应的弯矩和转角分别记为My和θy.对于PM组节点，因为存在不同的受力阶段，且在摩擦阶段呈线弹性，因此Y&K方法并不合适.将套管节点摩擦阶段结束时的转角视为屈服转角θy(取1.3°)，相应的弯矩为屈服弯矩My.采用屈服刚度Ky对比两组节点的初始刚度.表1给出了单调加载时各参数的计算结果，各个数据均为每组中两个试件所得结果的平均值.屈服刚度计算公式为

(3)

从图10和表1可以看出，与NM组节点相比，PM组套管节点的Mp没有明显不同.主要因为销栓类连接节点中，销栓截面尺寸越大，木材开裂破坏的可能性越大，当节点抗弯时，该不利影响就越明显.虽然期望通过构造措施，利用方套管顺纹承压来提高强度并延缓木材开裂，但在抗弯节点中，很难确保每个螺栓处的受力是纯粹的顺纹承压，因此导致木孔角部处出现应力集中，从而木材开裂.并且由于PM组节点中套管边长较大，最终列剪切破坏导致节点的强度和变形能力都未能充分发挥.

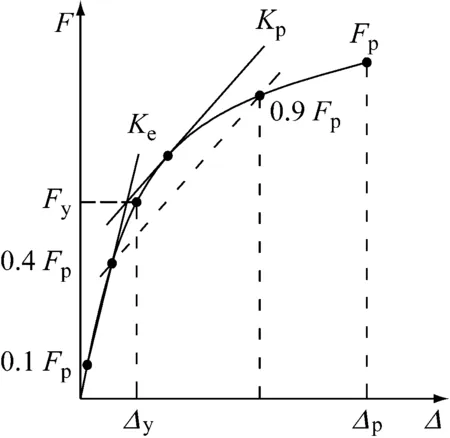
图11　Y&K方法计算屈服点原理示意图

从图10和表1屈服刚度的对比可以看出，PM组节点的Ky约为NM组节点的2倍.若取NM组的承载力与PM组的My相同(12.89 kN·m)，此时NM组的转角为2.35°，转动刚度为5.49 kN·m·(°)-1,约为PM组Ky的55%；如果以PM组的θy为控制目标，此时，NM组节点相应的抗弯承载力为7.38 kN·m，只有PM组承载力的57%.

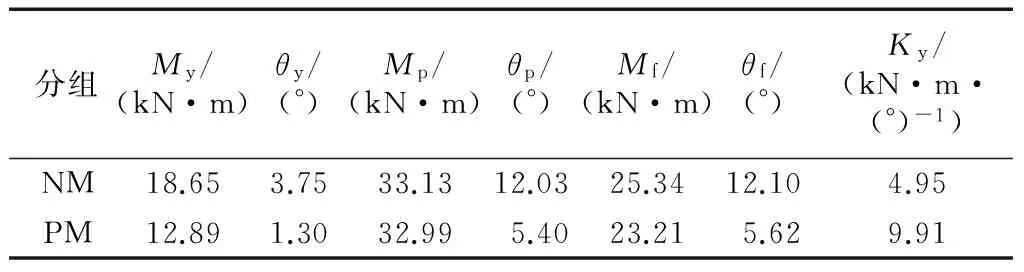
表1　单调加载参数计算结果对比

对于传统螺栓连接，需要克服孔洞间隙等因素造成节点的初始刚度过低.由于螺栓孔处木材存在局部承压，孔洞周围木材受力的非线性对节点的初始抗弯刚度起到控制作用.另外，在螺栓弯曲变形之后，螺栓和螺栓孔处木材间的承压作用在螺栓长度方向上分布是不均匀的，这也进一步降低了节点的抗弯刚度.

对于套管节点，在摩擦阶段依靠钢管和钢板间的摩擦及套管和木孔顺纹方向的接触，确保了初始传力.孔洞周围的木材在套管长度方向上的承压应力是均匀的，并且较大的套管直径使得承压应力相对较小，这也一定程度上提高了节点的抗弯刚度.

5　往复加载试验结果及分析

图12、图13和图14分别给出了往复加载时NC组、PC组节点的滞回曲线及其平均骨架曲线的对比.从图12和图13可以看出：NC组节点的滞回曲线整个过程中都有明显的捏缩现象；而PC组节点在0.4Δ的主循环之前具有较饱满的滞回曲线.通过图14中骨架曲线的对比发现，节点发生开裂破坏后，PC组节点的承载力下降更加明显，而NC组节点还存在一定的残余承载力，因为列剪切破坏相对顺纹劈裂破坏而言更加彻底，几乎丧失继续承载的能力，当然这也与连接件尺寸变大有关.

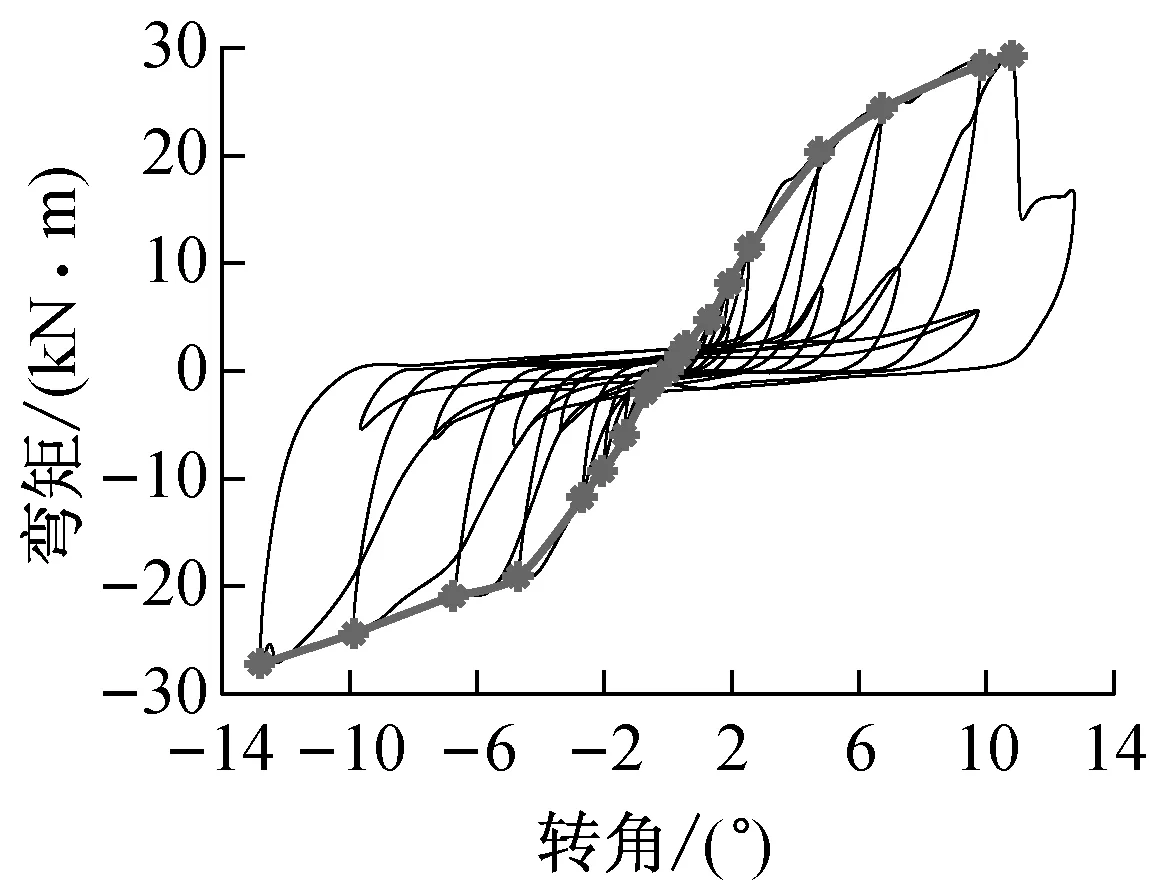
a NC-1

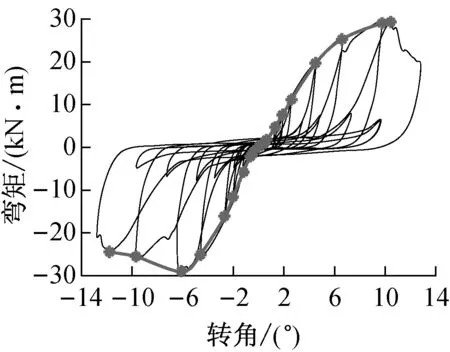
b NC-2

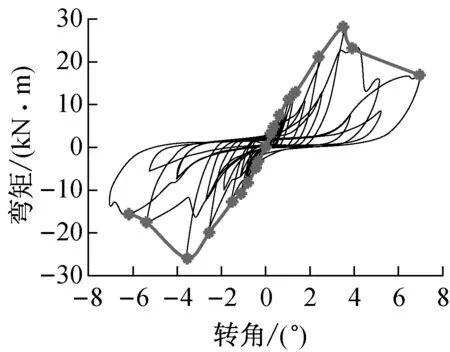
a PC-1

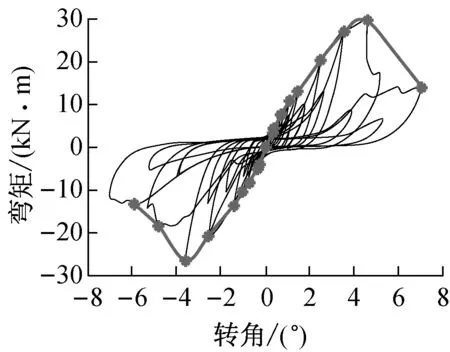
b PC-2

通过滞回曲线的割线刚度Ki(式(4))和等效黏滞阻尼系数εeq(式(5))的变化来衡量节点的损伤累积情况和耗能性能，Ki和εeq的计算结果见表2.忽略小变形时初始滑移导致的受力不确定性以及可能的制作、安装误差，因此只列出0.2Δ至2.0Δ主循环的计算结果进行对比.可以看出，NC组节点的Ki和εeq都要比PC组套管节点的小很多，在加载初期尤其突出.因为传统螺栓连接的孔洞间隙、不均匀销槽承压作用下木孔的扩大、螺栓的弯曲变形都会造成节点的刚度降低、滞回曲线的捏缩现象，并影响耗能能力；而套管节点中钢管和螺栓间的间隙只在滑移阶段之后才会对刚度产生明显影响，并成为滞回曲线捏缩现象的主要因素.

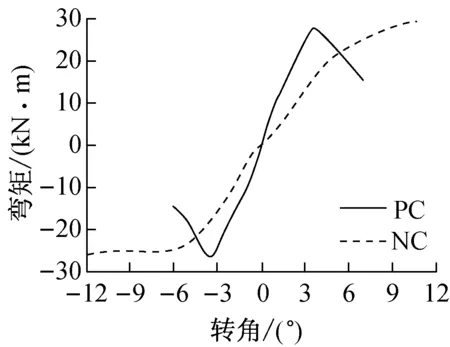
图14　往复加载平均骨架曲线对比

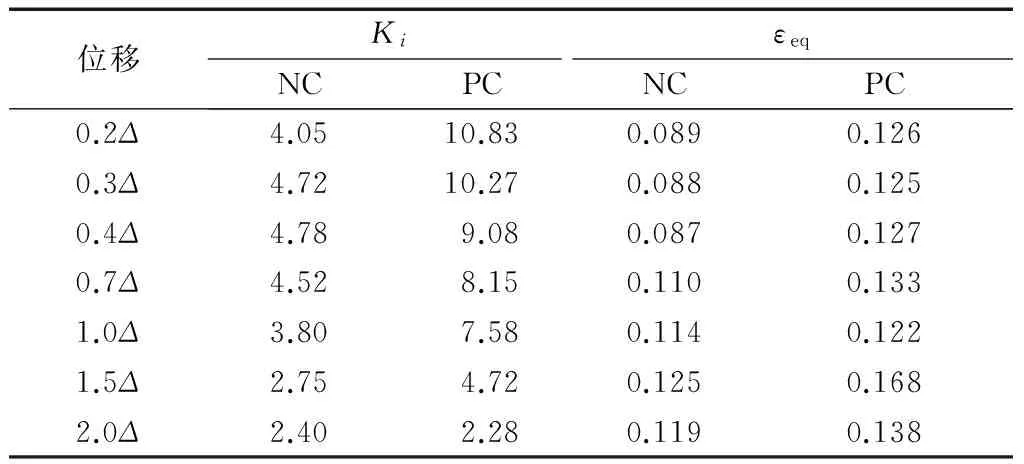
位移KiεeqNCPCNCPC0.2Δ4.0510.830.0890.1260.3Δ4.7210.270.0880.1250.4Δ4.789.080.0870.1270.7Δ4.528.150.1100.1331.0Δ3.807.580.1140.1221.5Δ2.754.720.1250.1682.0Δ2.402.280.1190.138

(4)

式中：Mi和-Mi分别为第i次主循环正、反向加载时的峰值弯矩;θi和-θi为对应峰值弯矩的转角.

(5)

式中：Ed代表节点在一个主循环中吸收的能量；Ep代表一个主循环总的变形能，见图15.

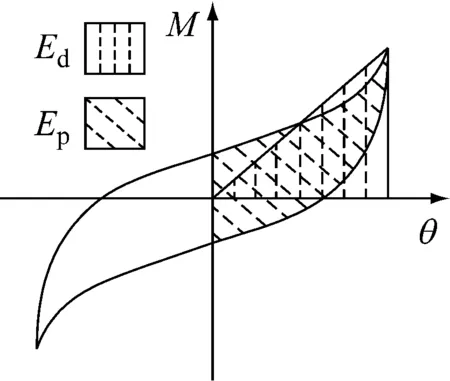
图15　等效黏滞阻尼系数计算示意图

为了便于理解分析套管节点受力过程的不同，图16给出了两组节点割线刚度和等效黏滞阻尼系数变化趋势的对比.从表2和图16中可以看出，对于NC组节点，在主循环为0.2Δ到0.4Δ的区间，其刚度呈缓慢增长的趋势，耗能能力处于较低的水平，表明节点从克服初始间隙到螺栓与孔壁充分接触基本处于弹性阶段，主要通过构件间的摩擦等进行少量的耗能.在0.4Δ到0.7Δ的区间，割线刚度开始出现下降，耗能开始明显增长，因为此时木材的承压开始逐渐出现不可恢复的塑性变形，但螺栓仍基本刚直.在0.7Δ到1.5Δ的区间，刚度开始明显衰退，耗能能力缓慢增长，表明孔洞处的木材已出现不可忽视的塑性变形和开裂等损伤累积，同时螺栓开始出现塑性弯曲变形.在1.5Δ到2.0Δ的区间，刚度持续快速退化，耗能能力出现下降，因为木材和螺栓在出现大量塑性变形的同时，裂缝不断扩展.

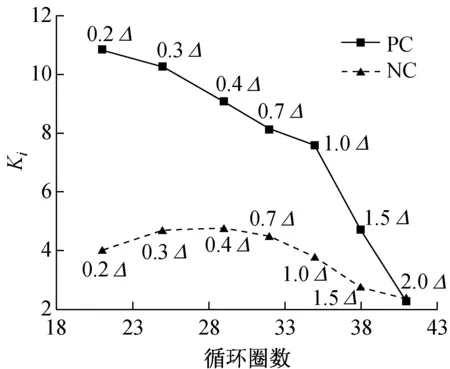
a 割线刚度

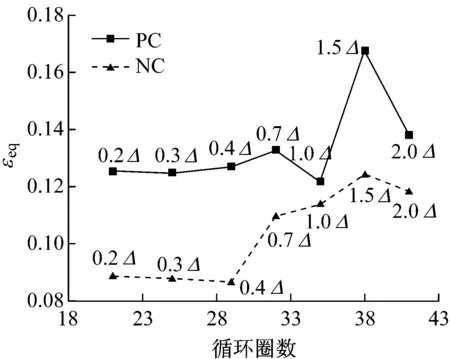
b 等效黏滞阻尼系数

对于PC组节点，主循环从0.2Δ到1.0Δ之间，节点尚未发生明显的开裂破坏，高强螺栓的预应力损失还较小，节点的割线刚度呈缓慢退化的趋势，这主要由木孔的开凿误差和轻微变形以及组件间的相对错动等引起.在1.0Δ到2.0Δ的区间，由于木材的彻底开裂以及高强螺栓的预应力损失，在往复荷载作用下，需要不断克服螺栓与套管间的间隙以及木材开裂产生的裂缝，节点刚度快速退化.对于PC组节点，从0.2Δ一直到1.0Δ之间，节点主要通过摩擦耗能，具有较好的耗能能力，其中从0.7Δ到1.0Δ，高强螺栓开始出现一定的预应力损失，因此耗能能力出现小幅下降.从1.0Δ到1.5Δ之间，节点木材出现明显破坏，通过开裂耗散了大量能量，εeq大幅增长；而从1.5Δ到2.0Δ的循环，裂缝已形成，节点处于完全开裂的状态，耗能能力出现明显下降.

6　结论

(1)与传统螺栓连接相比，套管节点仅在螺栓和木孔之间增加了钢套管，采用高强螺栓并施加预拉力，从而在钢管与钢板之间产生摩擦力，依靠二者间的摩擦以及套管和木孔间的承压传力，其受力可分为摩擦阶段、滑移阶段和典型阶段.

(2)方套管节点中由于套管横截面尺寸较大的原因，以及节点抗弯时难以确保每个螺栓处套管与木孔是纯粹的顺纹承压，因此导致木构件较早开裂，螺栓、钢管和木孔都没有出现明显变形，其强度未能充分发挥.最终，方套管节点主要的开裂模式为列剪切破坏.

(3)套管节点在摩擦阶段的受力曲线呈线性增长，进入滑移阶段后，刚度开始出现明显下降.不过由于制造安装误差的存在以及弯矩荷载下各个螺栓受力的不均匀，套管节点的阶段划分并不十分明显，但这对摩擦阶段的刚度几乎没有影响.

(4)套管节点的初始刚度得到明显提升，方套管节点的抗弯屈服刚度约为传统螺栓连接节点的2倍.

(5)套管节点在出现明显的预应力损失之前具有较饱满的滞回曲线和很好的耗能能力；随变形加大，摩擦力被克服，螺栓逐渐出现预应力损失，套管节点滞回曲线的捏缩现象逐渐变得明显.

[1]Lam F, Gehloff M, Closen M. Moment-resisting bolted timber connections[J]. Structures and Buildings, 2010, 163(4): 267.

[2]Rodd P D, Leijten A J M. High-performance dowel-type joints for timber structures[J]. Timber Construction, 2003, 5(2): 77.

[3]Leijten A J M. Development of reinforced joints with densified veneer wood[C/CD]∥ Proceedings of the 1991 International Timber Engineering Conference. London:[s.n.], 1991: 3.36.

[4]Haller P, Birk T, Offermann P,etal. Fully fashioned biaxial weft knitted and stitch bonded textile reinforcements for wood connections[J]. Composites: Part B, 2006, 37(4/5): 278.

[5]Blass H J, Schmid M, Litze H,etal. Nail plate reinforced joints with dowel-type fasteners[C/CD]∥ Proceedings of the World Conference on Timber Engineering. Whistler:[s.n.], 2000: 8.6.4.

[6]Blass H J, Schadle P. Ductility aspects of reinforced and non-reinforced timber joints[J]. Engineering Structures, 2011, 33: 3018.

[7]Leijten A J M. Locally reinforced timber joints with expanded tube fasteners[J]. Heron, 1999, 44(3): 131.

[8]Leijten A J M, Ruxton S, Prion H,etal. Reversed-cyclic behavior of a novel heavy timber tube connection[J]. Sructural Engineering, 2006, 132(8): 1314.

[9]HE Minjuan, ZHAO Yi, MA Renle. Experimental investigation on lateral performance of pre-stressed tube bolted connection with high initial stiffness[J]. Advaces in Structural Engineering, 2016, 19(5): 762.

[10]中华人民共和国建设部. GB 50005—2003 木结构设计规范[S]. 北京: 中国建筑工业出版社, 2003.

[11]Lam F, Schulte-Wrede M, Yao C C,etal. Moment resistance of bolted timber connections with perpendicular to grain reinforcements[C/CD]∥ Proceedings of the 10th World Conference on Timber Engineering. Miyazaki: [s.n.], 2008: 2.55.

[12]WANG Mingqian, SONG Xiaobin, GU Xianglin,etal. Rotational behavior of bolted beam-to-column connections with locally cross-laminated glulam[J]. Journal of Structural Engineering, 2015, 141(4): 1.

[13]American Society of Mechanical Engineers. ASTM D1761-88 Standard test methods for mechanical fasteners in wood[S]. West Conshohocken: ASTM International, 2000.

[14]American Society of Mechanical Engineers. ASTM E2126-09 Standard test methods for cyclic (reversed) load test for shear resistance of vertical elements of the lateral force resisting systems for buildings[S]. West Conshohocken: ASTM International, 2009.

[15]Yasumura M, Kawai N. Estimating seismic performance of wood-framed structures[C/CD]∥ Proceedings of 1998 IWEC. Switzerland:[s.n.], 1998: 5.

[16]Williams M, Mohammad M, Alexander S,etal. Determination of yield point and ductility of timber asemblies: In search for a harmonised approach[C/CD]∥ Proceedings of the 10th World Conference on Timber Engineering. Miyazaki: [s.n.], 2008: 2.62.

Rotational Performance of Pre-Stressed Multi-Bolted Glulam Connection with Square Tubes

ZHAO Yi1,2, HE Minjuan1, MA Renle1

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. Greenland Science and Technology Co. Ltd, Shanghai 200335, China)

This paper presents an experimental study on the moment resisting capacity and stiffness of the proposed pre-stressed bolted connection. High-strength bolts with square tubes were used as fasteners in such connections. Two groups of experimental tests were conducted with T-shaped glulam beam-to-column connections at monotonic and reversed cyclic loading. The failure mode, moment-rotation curve, strength, stiffness and energy dissipation property of the pre-stressed bolted connections with square tubes were obtained and compared with those of traditional bolted connections. The results show that the initial rotational stiffness of pre-stressed bolted connection increases significantly as a result of the friction between steel tubes and steel plate at the friction stage, and the energy dissipation capacity of pre-stressed bolted connection is also improved.

glulam structure; multi-bolted connection with square tubes; prestress; fraction; rotational stiffness

2015-10-16

国家自然科学基金(51378382)

赵艺(1987—)，男，工学博士，主要研究方向为木结构.E-mail: zhaoy0860@126.com

何敏娟(1963—)，女，教授，博士生导师，工学博士，主要研究方向为钢结构和木结构.E-mail: hemj@tongji.edu.cn

TU366.2

A