带上水线拉索绕流场的大涡模拟研究
杜晓庆, 李俊军, 顾 明, 何 平
(1.上海大学 土木工程系,上海 200072;2.同济大学 土木工程防灾国家重点实验室,上海 200092)
带上水线拉索绕流场的大涡模拟研究
杜晓庆1, 李俊军1, 顾明2, 何平1
(1.上海大学 土木工程系,上海 200072;2.同济大学 土木工程防灾国家重点实验室,上海 200092)
针对带上水线的拉索模型,采用大涡模拟方法研究了水线和拉索的气动性能与绕流场流态之间的内在关系.结果表明,带水线拉索的绕流场呈现三种不同的流态结构.当上水线位于0°~50°时,水线对拉索绕流场的影响不大;当上水线位于50°~70°时,拉索上表面剪切层在上水线上分离后会再附着在拉索表面形成分离泡,并使拉索上表面受到很大的局部负压作用;当水线处在70°~90°时,凸起的上水线会导致上侧剪切层分离后远离拉索上表面.分离泡在拉索上表面周期性地出现和消失是斜拉索风雨激振的主要原因.
拉索; 风雨激振; 大涡模拟; 上水线; 分离泡
自1989年日本的Hikami和Shiraishi[1]首先报道了斜拉桥拉索的风雨激振现象以来,世界各地的许多斜拉桥拉索在风雨共同作用下发生过这种大幅振动[2-4].斜拉索的大幅振动会严重危害拉索和斜拉桥的安全性.
各国研究人员通过现场实测、风洞试验和理论分析对拉索风雨激振现象进行较为广泛的研究,已获得了很多研究成果.但由于拉索风雨激振涉及空气、液体和固体等三种介质的耦合作用,并且受拉索表面条件、拉索倾角、风速、风向和雨量等多种因素的影响,因而对风雨激振的发生机理尚有不同观点.大部分研究者[1,5-8]认为,上水线在拉索上表面的出现及其沿拉索表面的振荡运动是拉索发生这种气动失稳现象的主要原因,可采用基于准定常假定的理论模型来解释风雨激振现象.但也有学者[2]认为,轴向流是斜拉索发生气动失稳的原因,认为准定常假定不适用风雨激振现象.作者对偏/斜光圆柱和带水线偏/斜圆柱进行的研究表明:轴向流会对拉索的气动性能产生一定的影响,但一旦上水线在拉索上表面形成之后,上水线对拉索的气动性能将起决定性的作用[9].
目前对上水线的受力情况和形成过程研究较少,上水线对拉索绕流场流态的作用机理尚不清楚.Du和Gu等[9]采用风洞试验,研究了上水线处在不同位置时上水线的表面风压和气动力作用规律.Lemaitre[10]基于滑移理论模型,研究了在风荷载作用下拉索表面水膜形态的变化.许林汕等[11]在Lemaitre模型的基础上,研究了考虑拉索运动影响的水膜形态变化和运动规律.Bi等[12]采用气液两相流理论和流体体积法研究了水线的形成过程.杜晓庆等[13]采用大涡模拟(LES)方法研究了作用在上水线上的风致摩擦力特性,并分析了水线的表面风压和摩擦力在上水线形成过程中的作用.
为了进一步澄清水线和拉索气动性能与绕流场流态之间的内在关系,本文采用大涡模拟方法,以带上水线拉索模型的气动性能和绕流场特性为研究对象,在亚临界区(雷诺数为1.4×105),研究了带水线拉索的气动力、表面风压分布和绕流场特性随水线位置的演变过程,研究了流态结构与水线和拉索气动力之间的内在联系,从带水线拉索绕流场的流态变化角度对拉索风雨激振的发生机理进行了探讨.
1 数值方法和计算模型
1.1控制方程和亚格子模型
大涡模拟(LES)方法中,大尺度涡通过滤波后的Navier-Stokes方程直接求解,小尺度的涡则采用亚格子尺度模型(SGS)模拟.与雷诺平均法(RANS)相比,大涡模拟方法可更好地模拟流场中的湍流漩涡,能捕捉到丰富的流场脉动信息.因此,为了准确地模拟带水线拉索周围的流场特性,本文采用大涡模拟方法进行研究.
经过滤波函数的滤波,可得到大尺度涡的不可压缩Navier-Stokes方程
(1)
(2)
亚格子应力τij采用Smagorinsky-Lilly的亚格子尺度模型,具有以下形式:
(3)
(4)
式中νt是亚格子尺度的湍动黏度,且
(5)
(6)
(7)
式中:Δi代表沿坐标轴i方向的网格尺寸;CS是Smagorinsky常数,本文取0.1.
1.2计算模型
考虑到上水线的出现是拉索发生风雨激振的关键因素,本文的计算模型只考虑上水线的作用,假定水线的形状和尺寸不随水线的位置发生改变.现场实测发现斜拉桥拉索发生大幅振动时雷诺数为0.5×105~2×105,因而本文的计算雷诺数取1.4×105(雷诺数根据拉索直径D和来流风速U0计算得到).另外,在本文的计算模型中,来流垂直作用于带水线拉索模型,即不考虑风向角的影响.
图1为带上水线拉索的计算模型示意图.图中,θu为上水线的位置角,θcyl为拉索表面各点的位置角,CD为拉索的平均阻力系数,CL为拉索的平均升力系数.上水线模型的外形和尺寸与文献[9]的风洞试验模型相近,水线表面为圆弧曲面,圆弧的直径d=0.13D,水线宽度为0.1D,高度为0.024D.
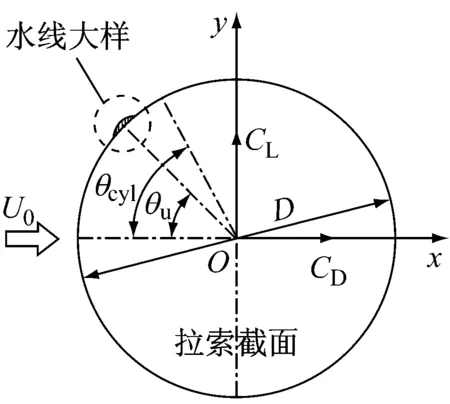

图1 带上水线拉索的计算模型
为了掌握上水线位置对拉索和水线气动性能的影响,根据上水线角度位置的不同,共计算了18个工况.其中:上水线位置角θu在0°~50°和80°~110° 之间每隔10°一个工况,50°~70°之间每隔5°一个工况,56°~64°之间每隔2°一个工况.
计算模型如图2所示,计算域的长、宽、高分别为28D,16D和D.其中,拉索中心距入口边界为8D,距离出口边界为20D,距上下侧面边界为8D,拉索展向长度为D.采用速度入口边界条件,出口边界采用自由流出边界,计算域上下侧面为对称性边界,拉索展向两端采用周期性边界条件,水线和拉索表面采用无滑移壁面边界条件.
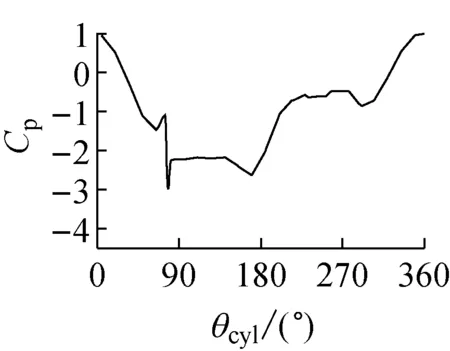
本文的网格方案和计算参数基于文献[16]的研究成果,近壁面最小网格为4×10-4D,量纲一时间步Δt*为 0.001(Δt*=ΔtU0/D,其中Δt为实际计算时间步),近壁面网格增长率为1.05.另外,为了验证圆柱展向长度对计算结果的影响,对三种不同的圆柱展向长度进行了比较(D,2D和4D).图3为这三种不同展向长度的圆柱表面平均风压系数Cp分布图,图中还给出了Cantwell和Coles[17]通过风洞试验得到的平均风压系数.从图3可见,三种计算值与风洞试验值之间的差异主要发生在θcyl=240°~360°,即圆柱的背风侧.并且随着圆柱展向长度的减小,计算值与风洞试验值之间的偏差有增大的趋势.这主要是因为圆柱展向长度的减小会增强绕流场沿圆柱展向的相关性,不能很好地反映三维圆柱绕流的三维流场特性,从而会造成圆柱背风面的负压偏大.考虑到大涡模拟的计算量大,而本文的计算工况又多,为了降低计算量,本文的带水线圆柱模型的展向长度取D,与文献[18]的计算模型相似.

a 计算域

b 近壁面网格

图3 光圆柱表面风压系数比较

1.3气动参数定义
拉索和水线表面的风压系数定义为
(8)
式中:p-po为当地风压和远前方上游压力之差.
对拉索表面的风压沿拉索周向进行积分,可得到作用在拉索上的气动阻力和气动升力,对气动力按照式(9)和式(10)量纲一化后可得到拉索的平均阻力系数CD和平均升力系数CL(其方向定义见图1)
(9)
(10)
式中:FD和FL分别为作用在单位长拉索上的气动平均阻力和气动平均升力.
2 计算结果及分析
2.1拉索的气动力系数
图4为作用在带上水线拉索上的平均阻力系数CL和平均升力系数CD随上水线位置角θu变化的曲线.图中还列出了文献[7,9]中的风洞试验结果.
从图4可见,本文采用大涡模拟计算得到的气动力系数曲线的变化趋势与文献[7,9]中的风洞试验结果相似.随着水线位置角的逐步增大,拉索的平均阻力系数和平均升力系数均经历了起伏和突变过程.与平均阻力系数相比,平均升力系数的变化则更为剧烈,经历了平稳段、上升段和下降段三个阶段.当水线位于θu=0°~50°时,拉索的平均升力系数接近于0,与不带水线的光滑拉索的平均升力系数相同;当水线位于θu=50°~70°时,平均升力系数则经历了先迅速上升,然后突然下降的过程,最大平均升力系数达到0.55左右;而当水线位于θu=70°~90°时,拉索则受到方向相反的非零平均升力的作用,最小升力系数为-0.15.通过风洞试验得到的文献[7,9]的平均升力系数同样经历了类似的变化过程,只是发生突变的水线位置范围以及气动力系数的数值与本文大涡模拟计算结果有所差异.
需要指出的是,与风洞试验值相比,本文采用大涡模拟得到的拉索平均升力系数与试验值吻合较好,但平均阻力系数的计算值较试验值偏大.这可能与计算模型与试验模型所采用的湍流度、表面粗糙度、雷诺数等的差异有关.Zdravkovich[14]指出圆柱的气动性能对来流湍流度、雷诺数和表面粗糙度等条件非常敏感.即便文献[7,9]均为风洞试验的结果,两者的气动力系数也有相当大的差异.另一方面,如1.2节所述,本文计算模型采用较小的展向长度会造成圆柱背风面负压的增大,从而会导致计算得到的平均阻力系数偏大.
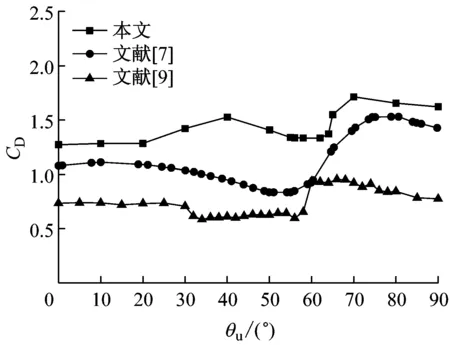
a 平均阻力系数

b 平均升力系数
2.2拉索的风压系数
由上文可知,上水线处在不同位置时,拉索的平均升力系数会经历三个不同阶段,图5~7给出了上水线位于θu=40°,58°和80°时带水线拉索表面的平均风压系数和脉动风压系数分布图.这三个典型的水线位置分别处在升力系数的三个不同阶段中.
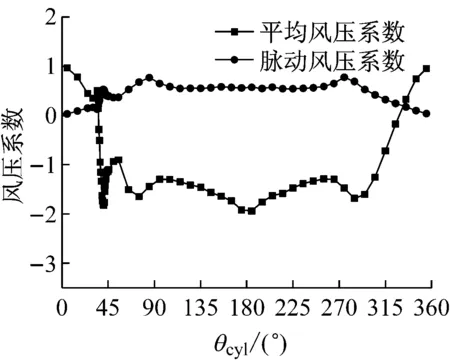
图5 θu=40°时拉索表面风压系数
Fig.5Wind pressures of cable with rivulet atθu=40°
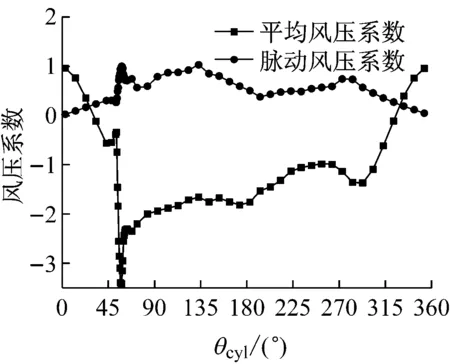
图6 θu=58°时拉索表面风压系数
Fig.6Wind pressures of cable with rivulet atθu=58°

图7 θu=80°时拉索表面风压系数
Fig.7Wind pressures of cable with rivulet atθu=80°
上水线位于θu=40°时(见图5),拉索上侧表面(θcyl=0°~180°)的风压系数与下侧表面(θcyl=180°~360°)相比,主要的差别发生在上水线位置附近(θu=40°附近),其他位置的平均风压系数在拉索的上下表面基本对称.脉动风压系数在θcyl=80°和280°附近有两个峰值,这两个峰值处在拉索上下表面的分离点附近,与表面不带上水线的光滑拉索的情况相近[15].这说明水线处在这个位置时,上水线不影响拉索上侧剪切层的分离点位置,因而对拉索气动性能的影响不大.
上水线位于θu=58°时(见图6),拉索上下表面的平均风压系数和脉动风压系数的形态均差别很大.对于平均风压系数,在上水线附近拉索受到很大负压的作用,拉索上表面负压最大处的风压系数达到-3.5,远大于拉索下侧受到的负压;在拉索的背风面,拉索上侧背风面(即θcyl=90°~180°)受到的负压也要远大于拉索下侧背风面(即θcyl=180°~270°);这种拉索上下表面平均风压系数的不对称性导致了带上水线拉索会受到很大的平均升力作用.对于脉动风压系数,拉索上侧表面在θcyl=58°和135°附近分别有两个峰值,前一个峰值对应于上水线位置,也是拉索上侧剪切层的分离点;而后一个峰值则对应于上侧剪切层在拉索表面再附后再次分离的分离点,详细的流场分析见2.3节;拉索下表面的脉动风压系数则在θcyl=280°附近有一个峰值,对应于拉索下侧的分离点.
上水线位于θu=80°时(见图7),对于平均风压系数,拉索上下表面风压分布的差别主要体现在水线位置附近,拉索表面风压在其他位置上基本是上下表面对称.对于脉动风压系数,拉索上表面的峰值处在水线位置,即拉索上侧的剪切层在上水线上发生分离;需要说明的是,在上水线处在θu=70°~90°时,上表面脉动风压系数的峰值均在水线位置,这说明凸起的上水线会控制拉索上侧剪切层的分离点,而拉索下表面的峰值均在θcyl=280°附近.
2.3作用机理分析
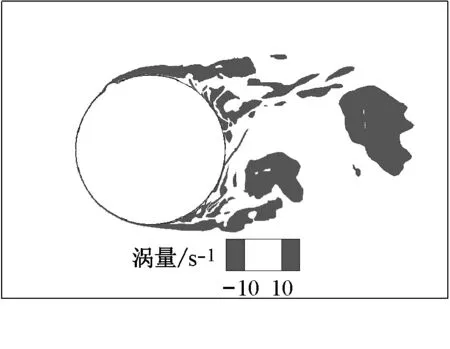
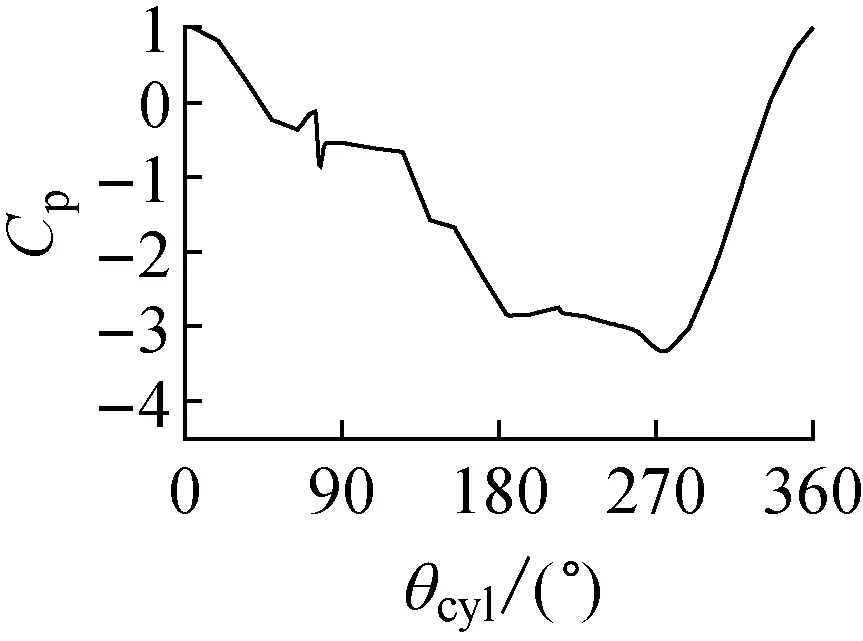
为了进一步分析带水线拉索气动性能处在三个不同阶段的流场作用机理,图8~10给出了水线位置角θu为40°,58°和80°时绕流场的瞬态流线图、涡量图、风压场以及拉索表面的瞬态风压系数图.图中,T1和T2分别是升力系数时程曲线上升力系数达到最小值和最大值的时刻,即对应于升力系数时程曲线的波谷和波峰时刻.
当水线位于θu=40°时,对于T1时刻(见图8a),从涡量图上看,拉索下侧的剪切流在分离后、近尾流区形成了强度很大的漩涡,从而导致拉索下侧绕流场处在负压区内,拉索下侧表面(θcyl=180°~360°)则承受很大的负压,最大负压系数达到-3.0;而在拉索的上侧,由于剪切流刚从拉索表面分离,还未能充分发展形成强度很大的漩涡,因而拉索上侧表面(θcyl=0°~180°)的最大负压系数较小,仅为-1.0左右.对于T2时刻(见图8b),则拉索上下侧的流场与T1时刻相反,拉索下侧表面的最大负压系数约为-1.0,而拉索上侧表面最大负压系数为-2.8左右.从T1和T2时刻拉索绕流场的瞬态流场信息和拉索表面的风压系数可见:在升力系数时程曲线的波峰和波谷时刻,带水线周围流场和拉索上下侧表面的风压系数基本处在一种反对称的状态,即上水线的存在并未对拉索的绕流场和气动性能造成很大影响,因而得到的带水线拉索的平均升力系数约为0.



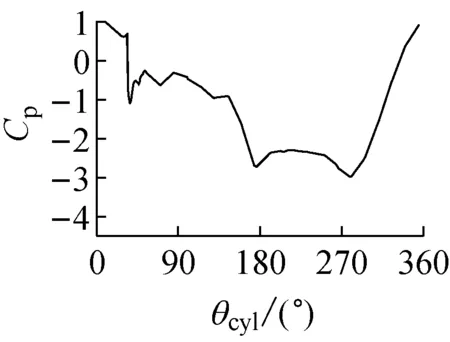
a T1时刻

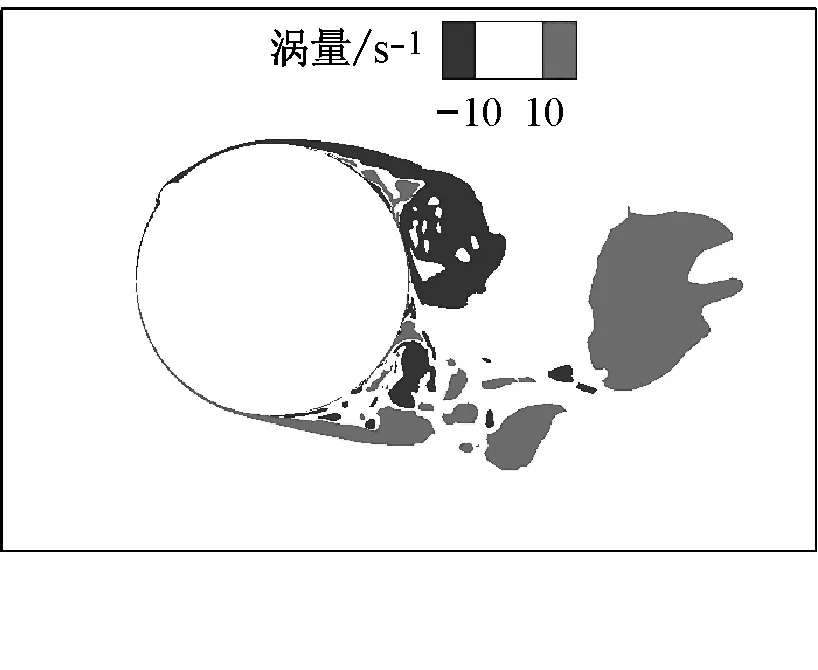
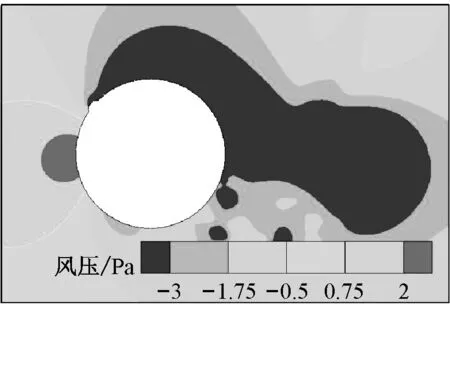
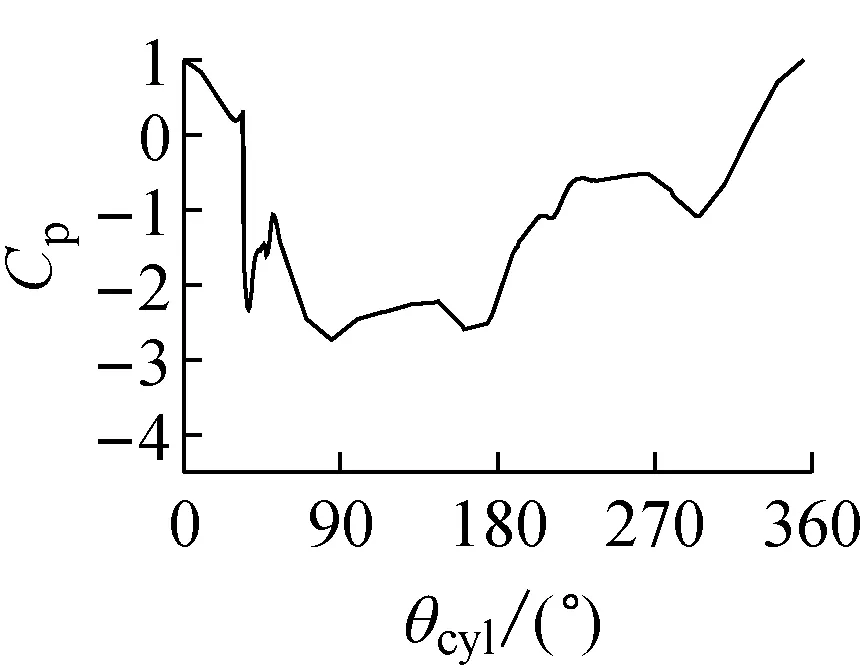
b T2时刻
Fig.8Instantaneous streamline, vorticity, pressure field around and pressure distribution of cable with rivulet atθu=40°



a T1时刻



b T2时刻
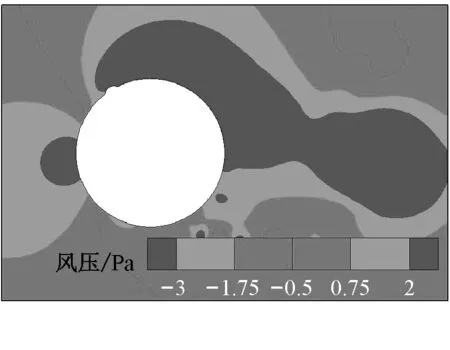
Fig.9Instantaneous streamline, vorticity, pressure field around and pressure distribution of cable with rivulet atθu=58°
当水线位于θu=58°时,对应于T1时刻(见图9a),从涡量图上看,拉索下侧的剪切流在分离后、近尾流区形成漩涡,但漩涡中心离圆柱表面的距离比θu=40°(图8a)时远,因而拉索下侧表面所受到的负压数值也较θu=40°时小;而对于拉索的上侧表面,从瞬态流线图和涡量图可以发现:由于受到上水线的干扰,上侧剪切层从拉索上表面的水线上分离后会再附到拉索表面,即形成 “分离泡”现象,使分离泡附近的拉索上表面承受很强的负压作用,最大的负压系数接近于-4.0.对于T2时刻(见图9b),拉索上表面同样发生了剪切流的分离再附现象,拉索上侧的绕流场呈现大面积的负压区;受到分离泡和尾流漩涡的共同影响,拉索上表面也出现数值很大的负压作用,最大负压系数已超过了-4.0.从上述分析可见,与上水线处在40°时相比,处在58°的上水线对拉索的绕流场和气动性能造成了很大影响,并且使得在一个涡脱周期内,拉索的上表面均受到数值很大的负压作用,从而导致带上水线拉索会承受较大的平均升力的作用,并且平均升力的方向指向拉索上侧.
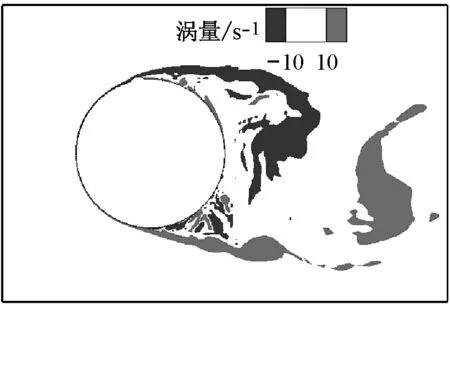
当水线位于θu=80°时,由图10的流线图和涡量图可见,T1和T2时刻拉索上表面均未发生分离剪切层的再附现象;T1和T2时刻拉索周围的风压场和拉索的表面风压系数分布图总体呈现反对称的形态,但T1时刻拉索下表面的负压系数比T2时刻拉索上表面的负压系数更大,从而导致带水线拉索受到平均升力系数的作用,但平均升力系数的方向指向拉索的下侧,其方向与θu=58°时的升力方向相反.从瞬态涡量图上看,这一反方向的平均升力的出现很可能是因为上水线对拉索上侧剪切层的影响造成的.水线在80°时,凸起的上水线会导致拉索上侧的剪切层在分离后远离拉索表面,因而剪切层对拉索上表面的影响相应减弱,拉索上侧表面受到的负压相对较小,导致拉索受到非零平均升力作用.



a T1时刻


b T2时刻
Fig.10Instantaneous streamline, vorticity, pressure field around and pressure distribution of cable with rivulet atθu=80°
从上文分析可知,当水线处在θu=50°~70°时,带水线拉索的绕流场发生了剧烈的变化,上水线对拉索的气动性能也会造成严重的影响.对于实际的斜拉桥拉索,如果在风雨共同作用下拉索上表面出现水线后,在漩涡脱落的涡激力和拉索振动的牵连惯性力作用下,上水线会在拉索上表面作振荡运动,如果水线振荡时其位置进出在θu=50°~70°这一区域,则在拉索的上表面会周期性地出现分离泡现象,拉索上表面分离泡影响区周期性地受到很大的负压作用,从而引发拉索发生振动.拉索的振动会进一步增大上水线在拉索表面的振荡幅度,增强水线振荡的规律性,进而引发大振幅的风雨激振的发生.
3 结论
采用大涡模拟方法,以带上水线拉索模型的气动性能和绕流场特性为研究对象,在亚临界区(雷诺数为1.4×105),研究了带水线拉索模型的表面风压系数、气动力系数和周围绕流场特性,研究了流场流态与带水线拉索气动性能之间的内在联系,从带水线拉索绕流场的流态变化角度对拉索风雨激振的发生机理进行了探讨.主要结论如下:
(1) 上水线处在θu=0°~50°时,上水线不影响拉索上侧剪切层的分离点位置,拉索的气动性能和绕流场特性基本不受上水线的影响.
(2) 上水线处在θu=50°~70°时,受到上水线的干扰,拉索上侧剪切层从上水线上分离后会再附到拉索表面,形成分离泡的现象.在分离泡影响范围内的拉索表面受到很大的负压作用,并导致拉索受到显著的非零平均升力系数的作用,平均升力的方向指向拉索上侧.
(3) 上水线处在θu=70°~90°时,拉索上侧剪切层在上水线上发生分离,上水线的位置决定拉索上侧剪切层的分离点位置.凸起的上水线会导致拉索上侧的剪切层在分离后远离拉索表面,因而分离剪切层对拉索气动性能的影响也较弱,拉索上侧表面受到的负压相对较小,带水线拉索受到较小的非零平均升力的作用,但平均升力的方向指向拉索下侧.
(4) 在漩涡脱落的涡激力和拉索振动的牵连惯性力作用下,上水线会在拉索上表面作振荡运动,如果水线振荡时其位置进出在θu=50°~70°这一区域,则在拉索的上表面会周期性地出现分离泡现象,拉索上表面分离泡影响区周期性地受到很大的负压作用,从而引发拉索发生振动.拉索的振动会进一步增大上水线在拉索表面的振荡幅度,增强水线振荡的规律性,进而引发大振幅的风雨激振的发生.
[1]Hikami Y, Shiraishi N. Rain-wind induced vibrations of cables in cable stayed bridges [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29(1): 409.
[2]Matsumoto M, Shiraishi N. Rain-wind induced vibrations of cables of cable-stayed bridge [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43(1): 2011.
[3]顾明,刘慈军,罗国强,等. 斜拉桥拉索的风(雨)激振及控制 [J]. 上海力学,1998, 19(4): 283.
GU Ming, LIU Cijun, LUO Guoqiang,etal. Rain-wind induced vibration of cables on cable-stayed bridges and its control [J]. Shanghai Journal of Mechanics, 1998, 19(4): 283.
[4]Ni Y Q, Wang X Y, Chen Z Q. Field observations of rain-wind-induced cable vibration in cable-stayed Dongting Lake Bridge [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(5): 303.
[5]Yamaguchi H. Analytical study on growth mechanism of rain vibration of cable [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 33(1): 73.
[6]Gu M, Du X Q. Experimental investigation of rain-wind-induced vibration of cables in cable-stayed bridges and its mitigation [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(1): 79.
[7]Matsumoto M, Yagi T, Saka S,etal. Steady wind force coefficients of inclined stay cables with water rivulet and their application to aerodynamics [J]. Wind and Structures, 2005, 8(2): 107.
[8]李永乐,徐幼麟,沈其民,等. 斜拉桥拉索风-雨致振动(I): 机理分析 [J]. 西南交通大学学报,2011,46(4): 529.
LI Yongle, XU Youlin, SHEN Qimin,etal. Rain-wind-induced vibration of cables in cable-stayed bridge (I): Mechanism analysis [J]. Journal of Southwest Jiaotong University, 2011, 46(4):529.
[9]DU Xiaoqing, GU Ming, CHEN Suren. Aerodynamic characteristics of an inclined and yawed circular cylinder with artificial rivulet [J]. Journal of Fluids and Structures, 2013, 43: 64.
[10]Lemaitre C. Thin water film around a cable subject to wind [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9): 1259.
[11]许林汕,赵林,葛耀君. 发生风雨激振拉索表面水膜形态数值分析和实测初探 [J]. 空气动力学学报,2011, 29(1):91.
XU Linshan, ZHAO Lin, GE Yaojun. Numerical analysis and real-time measurement of water-film on rain-wind induced vibration cable [J]. Acta Aerodynamic Sinica, 2011, 29(1):91.
[12]Bi J H, Lu P, Wang J,etal. Numerical simulation and analysis of the effects of water-film morphological changes on the aerodynamic lift of stay cables [J]. Journal of Fluids and Structures, 2014, 48: 376.
[13]杜晓庆, 何平, 顾明. 斜拉索上水线气动性能的大涡模拟研究[J]. 土木工程学报, 2014, 47(10): 12.
DU Xiaoqing, HE Ping, GU Ming. Investigation on aerodynamic characteristics of upper rivulet on stay cable using large eddy simulation [J]. China Civil Engineering Journal, 2014, 47(10): 12.
[14]Zdravkovich M M. Flow around circular cylinders [M]. Oxford : Oxford Science Publications, 1997.
[15]Nishimura H, Taniike Y. Aerodynamic characteristics of fluctuating forces on a circular cylinder [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(7): 713.
[16]Breuer M. A challenging test case for large eddy simulation: High Reynolds number circular cylinder flow [J]. International Journal of Heat and Fluid Flow, 2000, 21(5): 648.
[17]Cantwell B, Coles D. An exprimental study of entrainment and transport in the turbulent near wake of a circular cylinder [J]. Journal of Fluids and Mechanics, 1983, 136: 321.
[18]Behara S, Mittal S. Transition of the boundary layer on a circular cylinder in the presence of a trip [J]. Journal of Fluids and Structures, 2011, 27: 702.
Large Eddy Simulation of Flow Around Stay Cable with Upper Rivulet
DU Xiaoqing1, LI Junjun1, GU Ming2, HE Ping1
(1. Department of Civil Engineering, Shanghai University, Shanghai 200072, China; 2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
To understand the relationship between the flow field characteristics and aerodynamics of the cable with the upper rivulet, the flow around and aerodynamic characteristics of a cable model with an upper rivulet were investigated using large eddy simulation (LES) in the subcritical regime. The results show that there exist three distinct flow regimes with the rivulet located at different positions. In the range ofθu=0°~50°, the rivulet has little influence on the cable. In the range ofθu=50°~70°, with the interferences of the upper rivulet, the upper-side shear layer of the cable which is detached from the rivulet can reattach on the cable surface and form a single separation bubble at the upper side of the cable, which induces an asymmetrical pressure distribution on the cable surface. In the range ofθu=70°~90°, the upper-side shear layer detaches at the rivulet, which causes a lower negative pressure on the upper-side surface compared to those of the lower-side of the cable. It is concluded that the appearance and disappearance of the single separation bubble are the underlying reasons for the occurrence of the rain-wind-induced vibration (RWIV).
stay cable; rain-wind-induced vibration; large eddy simulation; upper rivulet; separation bubble
2015-11-19
上海市自然科学基金(14ZR1416000);上海市教委科研创新项目(14YZ004);国家自然科学基金(51578330)
杜晓庆(1973—),男,副教授,工学博士,主要研究方向为结构风工程. E-mail: dxq@shu.edu.cn
U448.27
A

