应变率效应对再生混凝土动态力学性能的影响

王长青， 肖建庄， 孙振平

(1. 同济大学 土木工程学院, 上海 200092； 2. 南阳师范学院 土木建筑工程学院，河南 南阳 473000;3. 同济大学 材料科学与工程学院, 上海 201804)



应变率效应对再生混凝土动态力学性能的影响

王长青1, 2, 3， 肖建庄1， 孙振平3

(1. 同济大学 土木工程学院, 上海 200092； 2. 南阳师范学院 土木建筑工程学院，河南 南阳 473000;3. 同济大学 材料科学与工程学院, 上海 201804)

通过约束再生混凝土单轴受压动态力学试验，研究了应变率效应对约束再生混凝土力学参数的影响.分析不同应变率下再生混凝土动态破坏特征以及受压应力-应变关系全曲线，可以发现：在不同应变率、再生粗骨料取代率或体积配箍率下，再生混凝土单轴应力-应变关系曲线的上升段基本一致，而下降段差异较为明显；随着应变率的提高或再生粗骨料取代率的增加，下降段曲线随之变陡，而随着箍筋配箍率的提高，下降段曲线明显随之趋于平缓.通过试验数据回归分析，提出约束再生混凝土受压峰值应力和峰值应变动态放大系数函数模型；随着应变率的提高，约束再生混凝土受压峰值应力和峰值应变均随之增大；而约束再生混凝土受压峰值应变动态放大系数增加幅值低于受压峰值应力动态放大系数的增加幅值；进一步分析了应变率效应对约束再生混凝土初始弹性模量的影响规律，确定了初始弹性模量和应变率的函数关系，并给出了初始弹性模量动态放大系数函数模型.随着应变率的提高，约束再生混凝土初始弹性模量动态放大系数随之增大，但其增长幅度要比受压峰值应力和峰值应变动态放大系数的增长幅度小.

再生混凝土; 约束； 动态试验; 应变率效应; 力学性能; 动态放大系数

混凝土材料有一定的率敏感性，在不同应变率下，具有不同的力学性能，包括材料的脆性、强度、刚度等性质均随加载速率而变化.在不同性质的动态荷载作用下，混凝土表现出不同的特性，如图1所示.可以看出，在地震作用下，混凝土的应变率一般能达到10-3s-1～10-2s-1量级，最大能达到10-1s-1左右[1].

关于混凝土动态特性的研究最早可上溯至1917年[2]的工作.比较一致的观点是随着应变率的提高，混凝土单轴抗压强度、初始弹性模量、峰值应力处的割线模量以及吸能能力随之增大，下降段的坡度趋于陡峭，泊松比无明显变化，应力-应变曲线的形状无明显区别.而峰值应力处的临界应变和极限应变的变化规律无定论.欧洲混凝土协会(CEB)[3]在总结多数试验成果的基础上，规定了一个准静态应变率，推荐了不同动态应变率下混凝土材料的抗压强度、峰值应变、弹性模量相对准静态应变率下的动态增大系数.

近些年来，再生混凝土技术的研究和开发已得到很大的发展.国内外学者关于再生骨料的基本性能[4]、再生混凝土材料的静态力学性能[5]、再生混凝土在静态荷载作用下的本构关系[6]等开展了系统的试验研究和理论分析.国内外对再生混凝土材料力学性能率敏感性方面的研究工作较少.肖建庄等完成了不同应变率下模型再生混凝土单轴受压试验[7]，研究表明，随着加载应变速率的提高，各模型的应力-应变曲线形状相似，峰值应力和弹性模量表现出增大的趋势，峰值应变的变化无明显规律.

本文通过约束再生混凝土方形截面短柱动态力学性能试验，测试约束再生混凝土在不同加载应变速率下的力学性能指标；分析约束再生混凝土单轴应力-应变关系曲线特征点参数(包括初始弹性模量、峰值点应力和峰值点应变)在不同应变率下的变化规律；初步建立约束再生混凝土力学性能参数动态放大系数函数模型.

1　试验设计

1.1骨料材料性能

再生骨料对再生混凝土的力学性能有重要的影响，在进行配合比之前，首先完成了再生混凝土中天然粗骨料和再生粗骨料性能指标的测试，如表1所示.细骨料选用公称粒径为0.075～5 mm的河砂，按细度模数划分为中砂，在使用前通过筛子过滤掉砂中较大的杂质，通过水洗处理掉砂中的泥块等细微颗粒，通过风干除去砂中的水分，砂的含水率为0.粗骨料选用天然和再生粗骨料，公称粒径大小范围为5～10 mm，如图2和3所示.由表1中的数据可以看出，再生粗骨料的吸水率要远高于天然粗骨料的吸水率.在使用前同样对天然粗骨料和再生粗骨料进行筛分过滤、水洗和风干处理.

图2　天然粗骨料

图3　再生粗骨料

1.2配合比设计

再生混凝土强度等级为C30.由于再生粗骨料有较高的吸水率，配合比设计时应考虑计入再生混凝土粗骨料的附加用水，再生粗骨料附加用水含量根据其饱和面干时的含水量确定.在本试验中测得的再生粗骨料吸水率为5.4%，含水率为1.6%(见表1).水泥选用强度等级为42.5R的普通硅酸盐水泥，水选用自来水，外加剂采用VIVID-500(A)聚羧酸超塑化减水剂，固体质量分数为40%.混凝土塌落度值控制在180～200 mm范围内.本试验中按再生粗骨料取代率R分别为0，30%和100%三种配合比进行设计.表2给出了不同取代率下每立方米混凝土各组分的用量.

表2　再生混凝土配合比

1.3试件设计和制作

试验试件设计成高宽比为3∶1的再生混凝土方形截面短柱，其横截面尺寸为150 mm×150 mm，高度为450 mm.试件设计成约束和非约束两种类型，约束再生混凝土试件中配置A和B两种不同形式的箍筋，A代表方形箍筋，B代表菱形复合箍筋，箍筋选用镀锌铁丝，直径为4 mm.试件尺寸和箍筋形式如图4所示.试件设计参数见表3.所有试件的制作均在实验室完成，在外界环境温度条件下分4批进行人工浇注，机械振捣，采用木模板，24 h后拆模，并在混凝土标准养护室养护28 d.每批试件均预留出3组棱柱体(100 mm×100 mm×300 mm)试件和3组立方体试件(150 mm×150 mm×150 mm)，测试再生混凝土的材料性能.图5为现场施工照片.

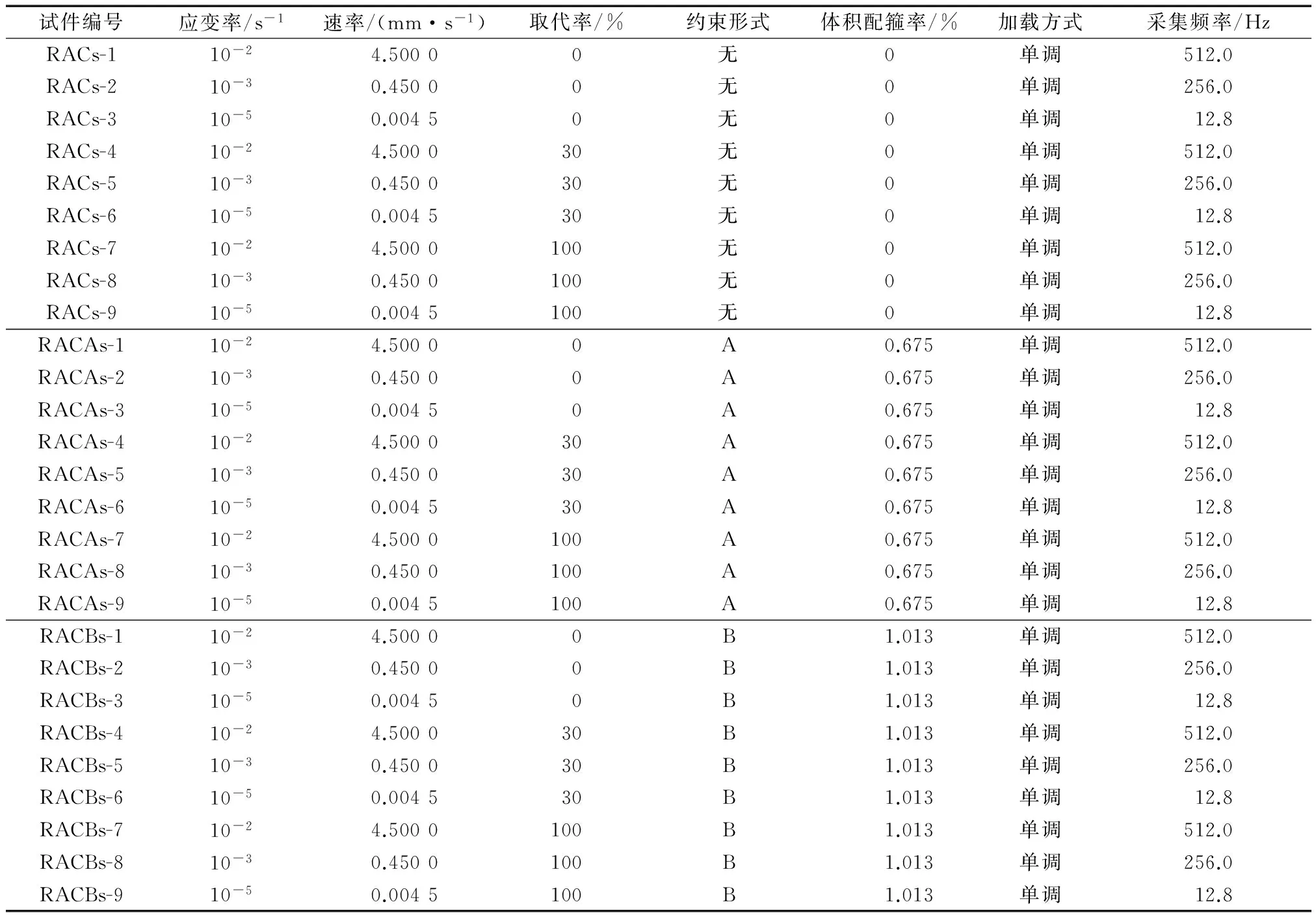
表3　测试试件设计参数

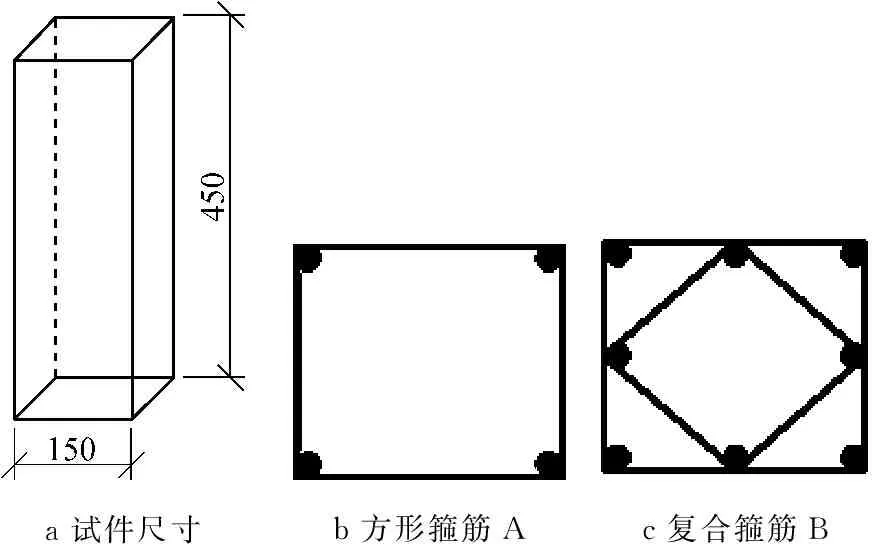
a试件尺寸b方形箍筋Ac复合箍筋B

图4　试件尺寸和箍筋形式(单位：mm)

图5　试件制作

1.4试验设备

试验在MTS 815.04液压伺服试验机上进行.试验机中自带一套数据采集系统、高精度荷载传感器和高精度位移传感器.试验中采用自带位移传感器测试压头之间试件的轴向变形；试验中附加的引伸计(如图6所示)作为测试试件中部变形的应变传感器，测量在标定距离为100 mm处的试件变形.引伸计与试验机自带的传感器均采用同一套数据采集系统，测量数据均由试验机配套程序自动记录，实现不同通道的数据同步采集.

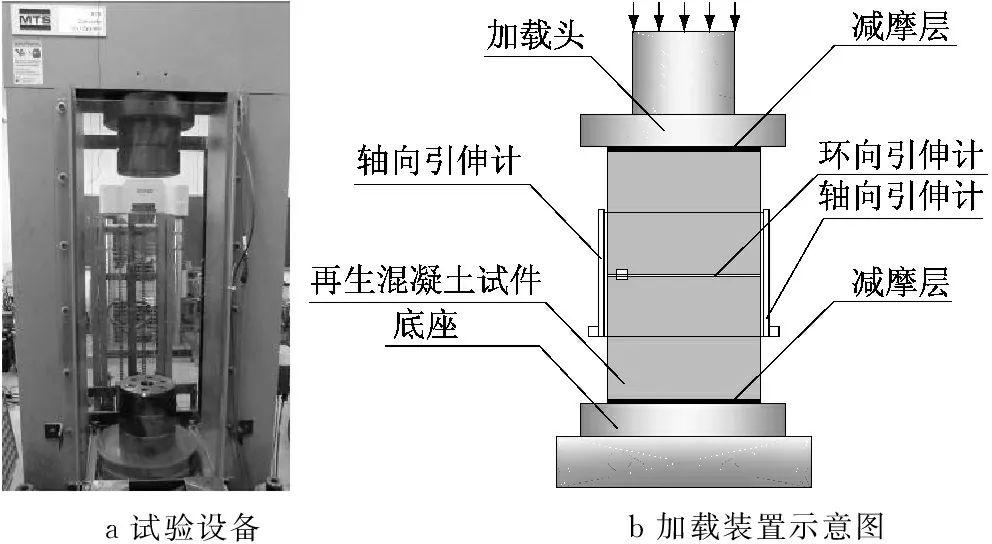
a试验设备b加载装置示意图

图6再生混凝土单轴受压加载试验设备

Fig.6Test setup of uniaxial compressive loading

1.5加载制度

试验采用的加载方式为单轴动态单调受压加载，加载过程中采用位移进行控制，试验终止位移由再生混凝土极限应变计算公式获取，取为5 mm.整个试验中采用3种加载速度，分别为0.004 5，0.45和4.5 mm·s-1.相应的应变率分别为10-5，10-3和10-2s-1，其中把10-5s-1定义为准静态应变率(基准应变率).通过变应变率加载试验，主要研究约束再生混凝土的动态力学性能，分析性能参数随应变率的变化规律.加载方式和相应的试件编号详见表3.为消除加载钢板对试件产生的横向约束影响，正式加载前，在试块的底部和顶部分别放置2层0.1 mm厚聚四氟乙烯薄膜作为减摩层，将试样放置在试验机的底座上，进行几何和物理对中，即将试件的中心与下压板中心对准后进行施压，加载至基准应力为0.5 MPa的初始荷载值，保持恒载60 s，再连续均匀地加荷载至承载力估计值30%，校正试件和仪器仪表使其对中后卸载.当对中满足要求后，以与加荷速度相同的速度卸荷至基准应力0.5 MPa，保持恒载60 s，然后用同样的加荷和卸荷速度以及60 s的保持恒载，进行两次反复预压.

2　动态试验

2.1试验数据处理

再生混凝土受压试验过程中，试件会产生一定的附加变形，这些附加变形主要由以下几种可能因素引起：①为消除加载头对试件侧向约束的影响，试验中在试件上下两端分别放置了减摩层，由于减摩层自身刚度较小，在加载过程中会产生一定的变形；②由于试验机加载压盘由螺钉连接组成，其连接空隙在加载过程中会发生一定程度的变形；③在试验前，采用不同细度的砂布对试件端部进行了抛光处理，但由于试件变形精度较高，试件上下端表面平整度不够会产生一定程度的附加变形；④试验设备自身刚度不够，也会使试件产生一定程度的变形.

在试验数据处理时，通过附加的引伸计采集系统，对试验中产生的附加变形统一做了标定.图7给出了力与附加变形之间的关系，进而确定了力-附加变形数学关系表达式为

(1)

由附加变形，可以计算出试件实际变形

(2)

式中：Δa，Δg和Δ分别代表附加变形、总变形和试件实际变形；P表示外加荷载.

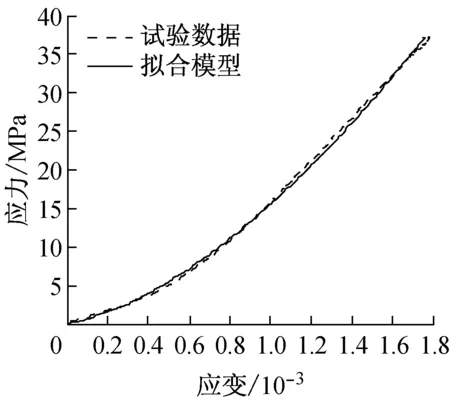
图7　附加变形标定

2.2破坏特征

不同应变下再生混凝土在受压荷载下的破坏特征差异性很大.低应变率下，随着外荷载的增加，再生混凝土试件遭受一定的损伤，表现在再生混凝土试件表面出现细微的竖向和斜向裂缝，随着试件损伤程度的加剧，裂缝进一步延伸和扩大，并伴有新的裂缝出现.整个破坏过程，裂缝发展速度较平缓，在破坏荷载下，试件上有贯通裂缝形成，如图8a所示.低应变率下，损伤主要发生在粗骨料和砂浆界面，而粗骨料鲜有发生断裂，断裂界面如图8b所示.随着高应变率的提高，试件损伤速度也随之加快，裂纹在试件表面出现后，会迅速发展，形成一条竖向或斜向劈裂贯通裂缝，或者在没有任何裂缝出现的前兆下，试件局部混凝土会被压溃脱落.在高应变率下，整个破坏过程，裂缝发展速度较快，试件破坏时会伴随很大的混凝土爆裂声.图9a表示应变率为10-2s-1下的再生混凝土裂缝开展照片.高应变率下，再生混凝土断裂界面比较平整，再生粗骨料在破环截面发生断裂，图9b所示应变率为10-2s-1下的再生混凝土断裂界面照片.

a裂缝开展b断裂界面

图8试件破坏描述(应变率为10-5s-1)

Fig.8Description of specimen failure

(strain rate=10-5s-1)

2.3试验曲线

应力-应变全曲线能够全面地体现再生混凝土材料在加载过程中的力学性能，基于单轴应力-应变关系曲线可以进行特征点参数分析.将每组试验结果的平均值列于同一坐标系中，得到不同应变率作用下的再生混凝土单轴应力-应变关系全曲线均值曲线，并确定了应力-应变关系曲线的特征点参数.

a裂缝开展b断裂界面

图9试件破坏描述(应变率为10-2s-1)

Fig.9Description of specimen failure (strain rate=10-2s-1)

图10分别给出了不同再生粗骨料取代率(R)和体积配箍率条件下再生混凝土单轴受压动态应力-应变关系全曲线.由图中的曲线可以看出：

(1) 动力加载条件下的单轴受压应力-应变关系曲线形状仍然符合经典单轴受压试验的基本描述；

(2) 试验数据的均值曲线具有较好的连续性和光滑性，说明试验曲线具有内在的一致性；

(3) 动力加载条件对试验结果的影响主要体现在混凝土抗压强度以及变形特性方面；

(4) 不同再生粗骨料取代率下再生混凝土单轴应力-应变关系曲线形状无明显区别，曲线的上升段基本一致，而下降段差异较为明显；

(5) 随着再生粗骨料取代率的增加，下降段曲线随之变陡.临界应变随再生粗骨料取代率提高而增大，而抗压强度变化不明显；

(6) 不同配箍率下，应力-应变关系曲线的上升段基本一致，而下降段差异较为明显，随着箍筋配箍率的提高，下降段曲线明显随之趋于平缓；

(7) 在应变率10-5，10-3和10-2s-1下，再生混凝土应力-应变关系曲线的上升段基本一致，而下降段差异较为明显，随着应变率的提高，下降段曲线随之变陡，峰值点应力和相应应变随之增加；

(8) 初始弹性模量和峰值应力处的割线模量以及吸能能力随应变率的提高而随之增大；

(9) 随着加载应变速率的提高，再生混凝土的塑性变形能力和延性性能反而降低.

3　应变率效应分析

通过试验数据获取的再生混凝土应力-应变全曲线，重点对再生混凝土力学性能参数进行数据回归分析，研究其随应变率变化的分布规律，为了便于分析应变率效应对再生混凝土力学性能的影响，这里引入动态放大系数DIF(dynamic increase factor)，即动态荷载下力学性能指标与准静态加载下力学性能指标的比值.

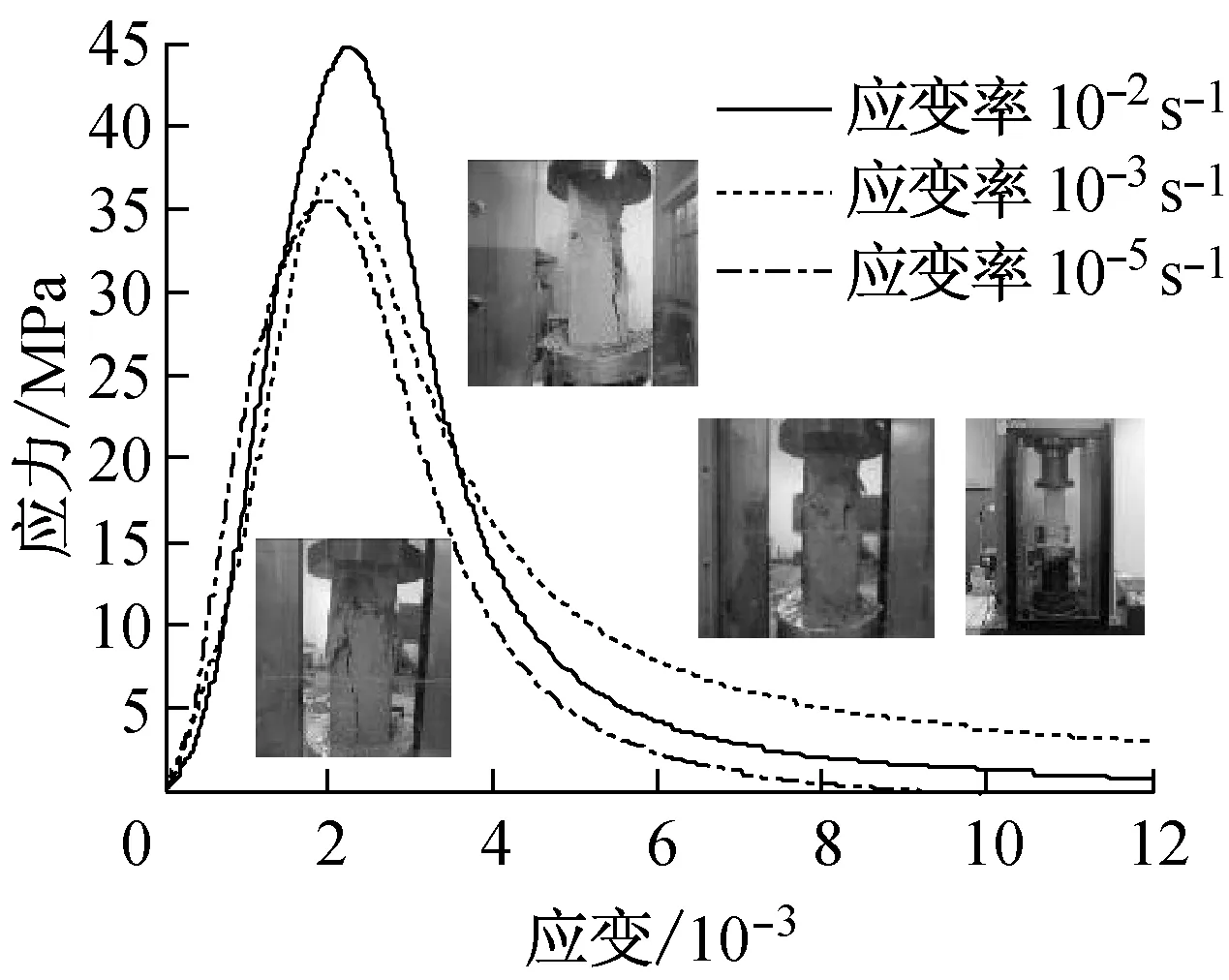
a 非约束, R=0

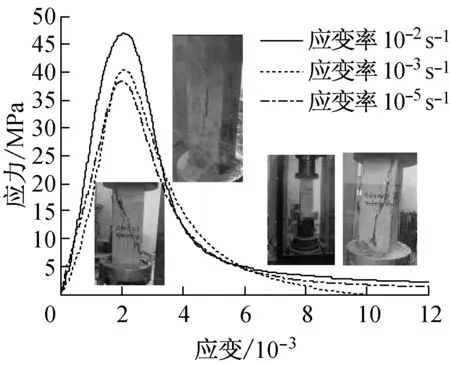
b 非约束, R=100%

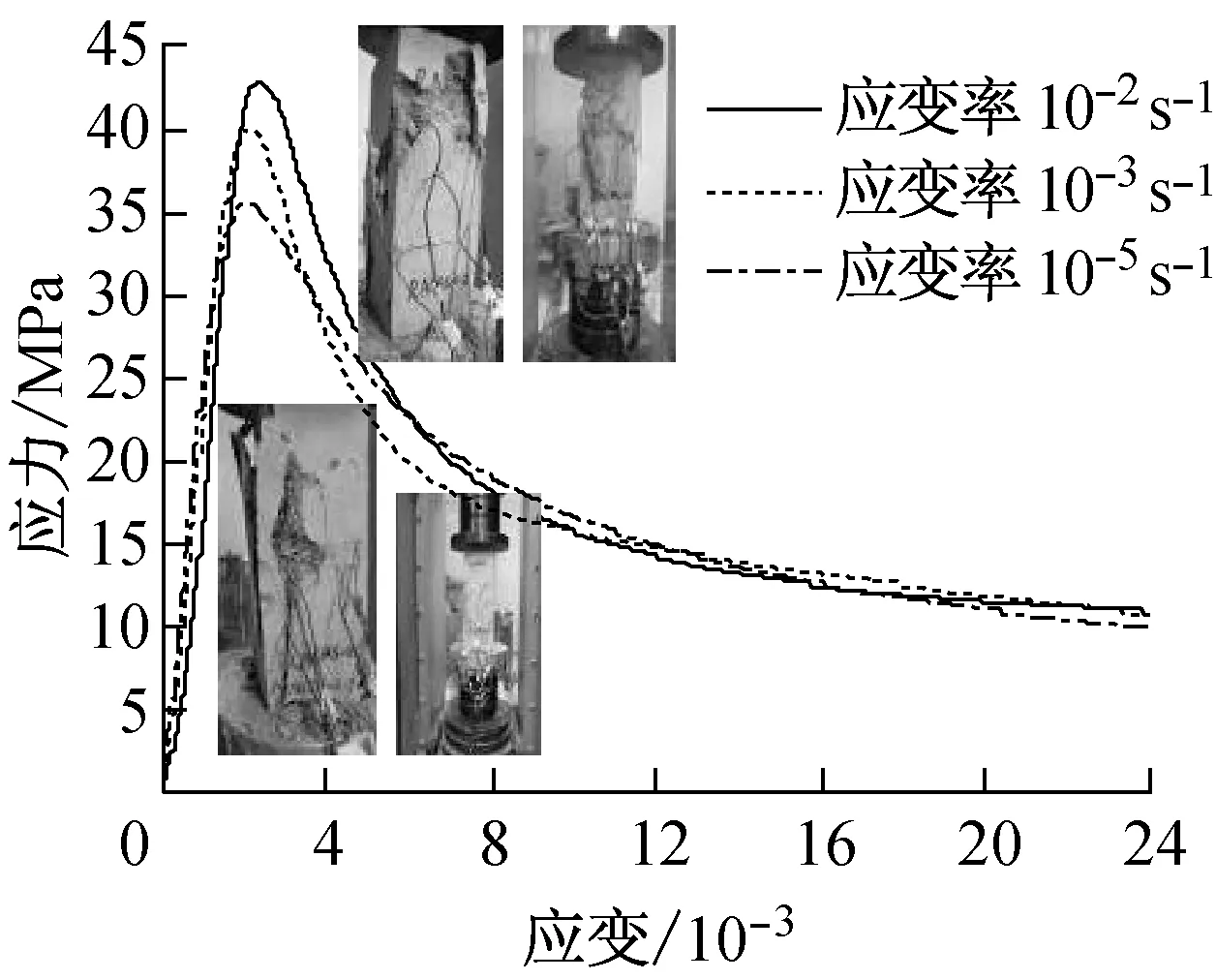
c A类约束, R=0

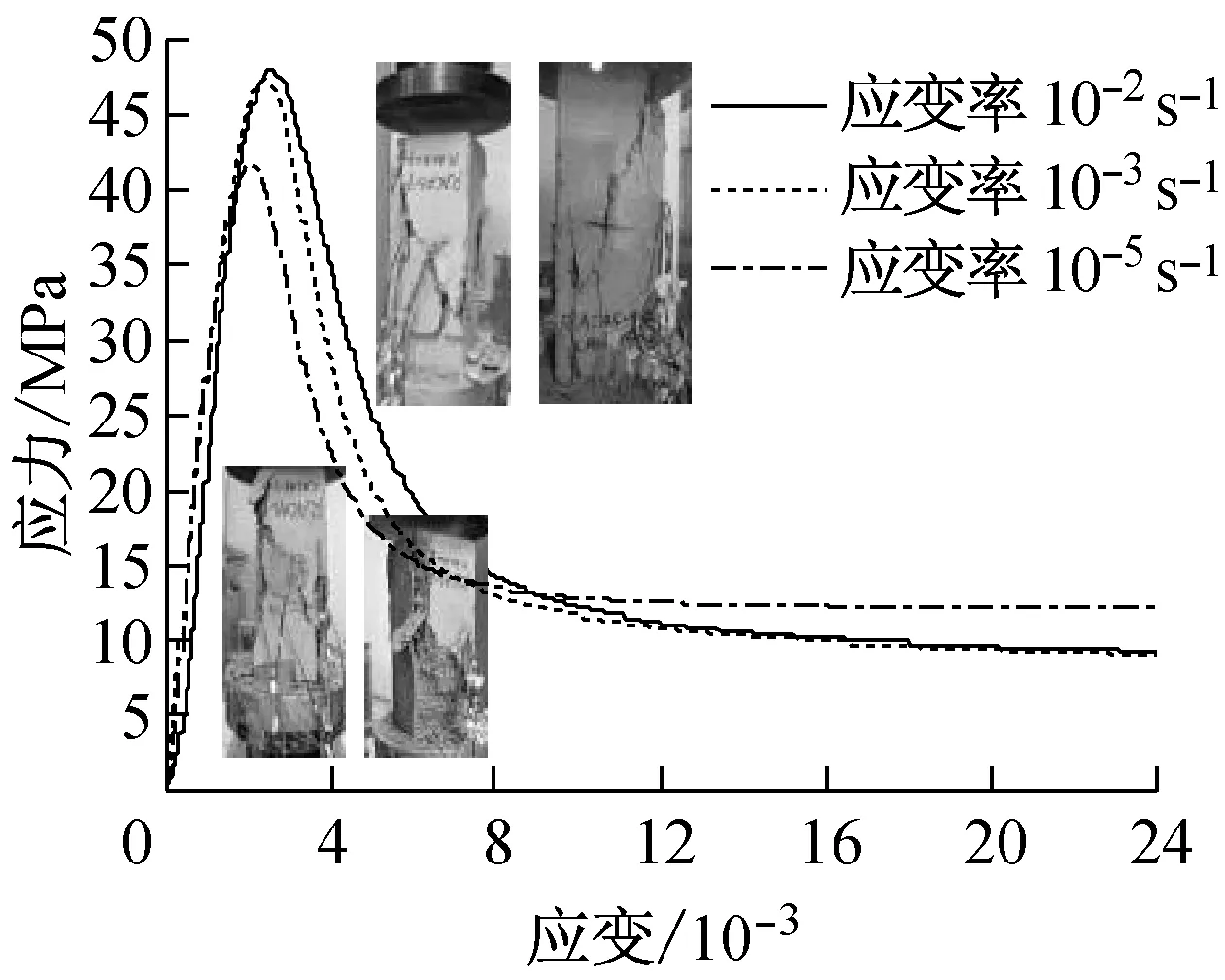
d A类约束, R=100%

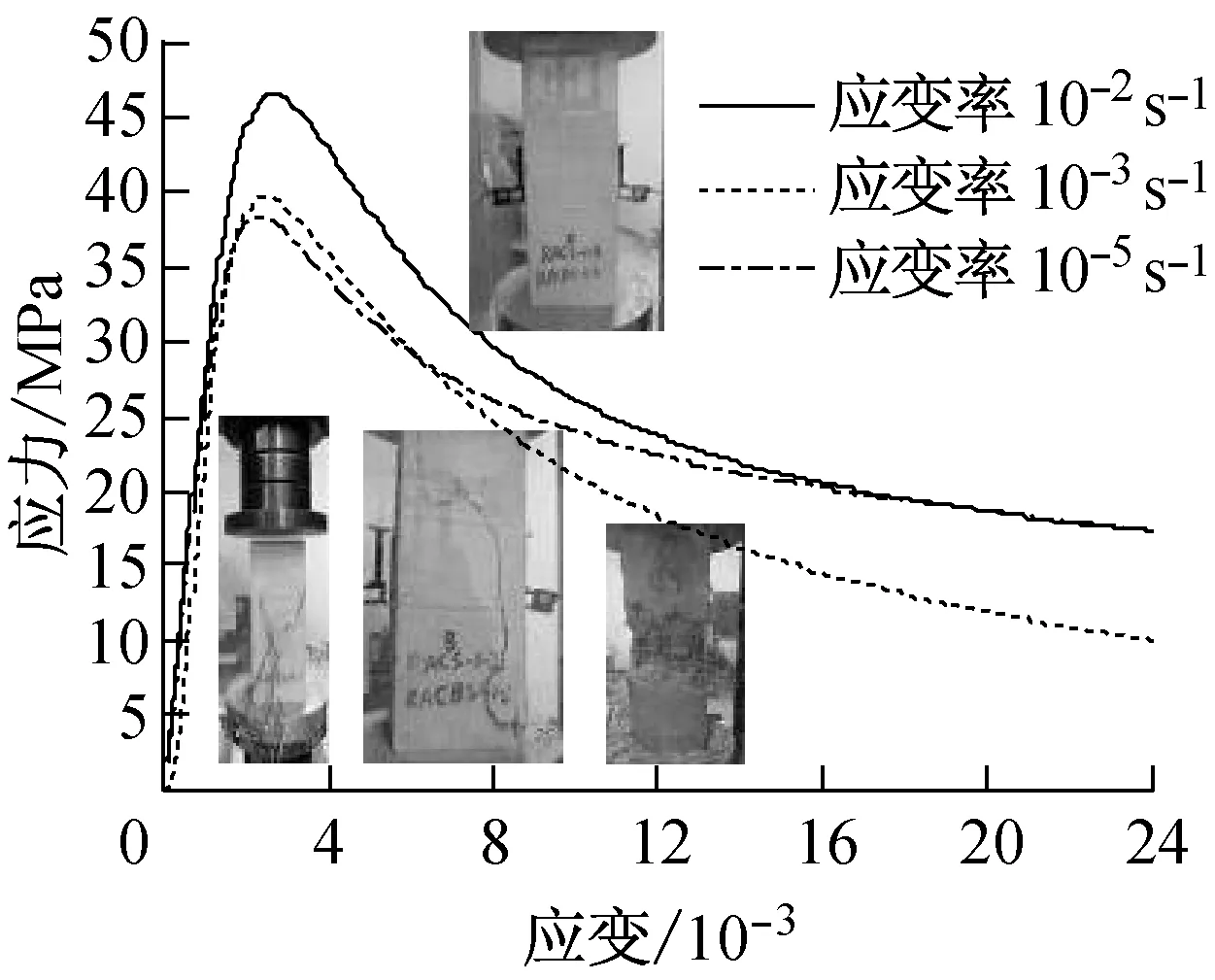
e B类约束, R=0

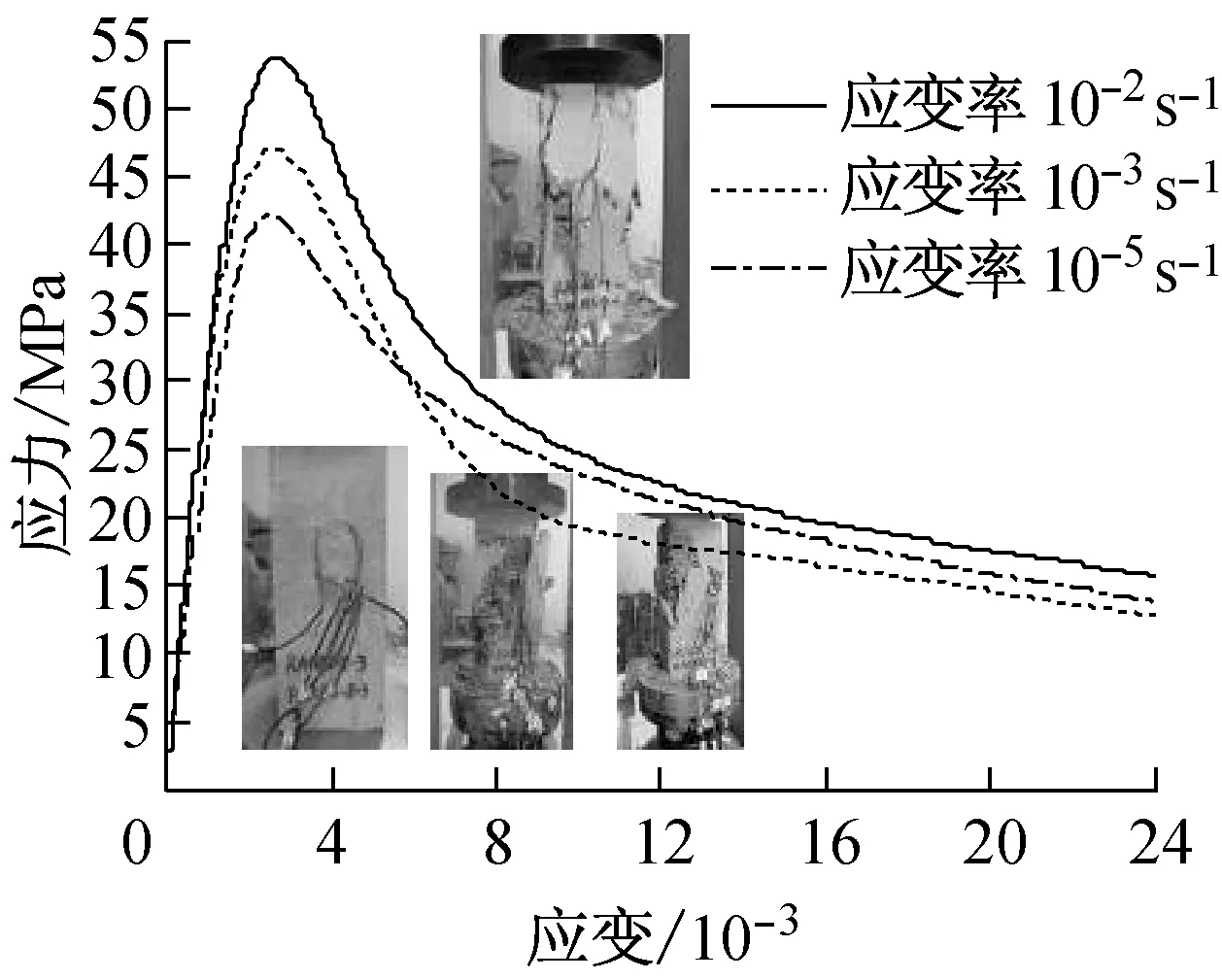
f B类约束, R=100%

3.1受压峰值应力

受压峰值应力是描述混凝土力学性能的重要力学参数，取不同应变率下每组试件应力最大值的均值，从图10所示的不同应变率下应力-应变均值曲线可以看出，应变率效应对再生混凝土受压峰值应力的影响非常显著.根据图中由试验数据获取的单轴应力-应变关系全曲线，获得不同条件下再生混凝土受压峰值应力，计算分析受压峰值应力动态放大系数随应变率的变化规律，并给出了相应的数据拟合曲线，如图11所示.通过对图11中数据回归分析，初步提出约束再生混凝土受压峰值应力动态放大系数函数模型，其数学表达式如下：

(3)

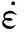
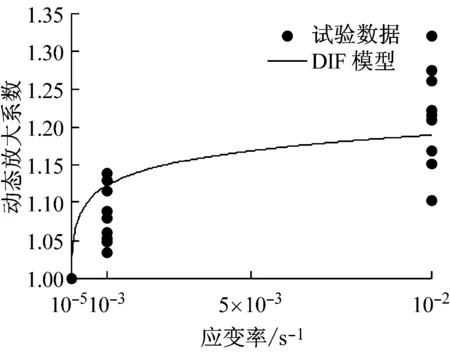
图11　约束再生混凝土受压峰值应力动态放大系数

表4给出了受压峰值应力动态放大系数函数模型参数取值，通过公式 (3)和表4中的数据，计算出不同应变率下归一化的受压峰值应力动态放大系数，如表5所示.可以看出，随着加载应变速率的提高，约束再生混凝土受压峰值应力随之增大.

3.2受压峰值应变

受压峰值应变即受压峰值应力对应的应变.对受压试验而言，应变率对峰值应变的影响还没有明确的结论，主要存在以下三种观点：①随着应变率提高，受压峰值应变随之减小[8]；②随着应变率提高，混凝土受压峰值应变基本保持不变[9]；③随着应变率的提高，受压峰值应变随之增加[10].

表4　受压峰值应力动态放大系数函数模型参数

表5　量纲一化的受压峰值应力动态放大系数

应变率效应对再生混凝土受压峰值应变的影响，国内外学者研究还非常少，鲜有文献报道.本文基于完成的再生混凝土动态受压试验，调查分析应变率效应对再生混凝土受压峰值应变的影响规律.同样，根据图10中由试验数据获取的单轴应力-应变关系全曲线，获得不同条件下再生混凝土受压峰值应变，计算分析受压峰值应变动态放大系数随应变率的变化规律，并给出了相应的数据拟合曲线，如图12所示.通过对图12中数据回归分析，初步提出约束再生混凝土受压峰值应变动态放大系数函数模型，其数学表达式如下：

(4)

式中：kεc表示受压峰值应变动态放大系数；φ为函数模型参数.

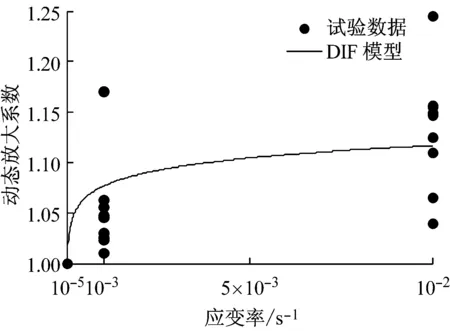
图12　约束再生混凝土受压峰值应变动态放大系数

表6给出了受压峰值应变动态放大系数函数模型参数取值，通过公式 (4)和表6中的数据，计算出不同应变率下量纲一化的受压峰值应变动态放大系数，如表7所示.通过分析可以看出，在本研究中应变效应对再生混凝土受压峰值应变的影响明显，随着加载应变速率的提高，约束再生混凝土受压峰值应变动态放大系数随之增大，但其增加幅值低于受压峰值应力动态放大系数的增加幅值.目前，有关动态荷载下再生混凝土力学性能的研究还很少，可利用和参考的试验数据资源非常有限，基于现有的可靠试验数据的深入分析，可初步获得约束再生混凝土峰值应变随应变率变化的一些结论，为进一步的研究工作提供技术和理论支撑.

表6　受压峰值应变动态放大系数函数模型参数

表7　量纲一化的受压峰值应变动态放大系数

3.3初始弹性模量

弹性模量是混凝土的变形性能指标，是描述混凝土材料单轴应力-应变关系特征的又一个重要参数.关于弹性模量取值，可以取应力-应变全曲线上某点的切线模量，也可通过应力-应变曲线上某点的割线模量确定取值.为了方便描述，很多研究者采用后者描述方法来定义弹性模量的代表值[7,11].为定义再生混凝土初始弹性模量，首先通过对再生混凝土单轴应力-应变关系曲线的试验数据回归分析，构建曲线函数方程，然后通过对曲线方程求导，来确定初始弹性模量.因此，基于图10中应力-应变关系全曲线，对曲线的上升段进行拟合分析，获取相应的拟合曲线，如图13所示.根据图13中的曲线，初步构建出约束再生混凝土单轴应力-应变关系曲线上升区段函数模型，公式 (5)给出了曲线方程的数学关系表达式.通过公式 (5)，进而推导出约束再生混凝土动态初始弹性模量，公式 (6)给出了其相应的函数方程数学关系表达式，公式中确定了初始弹性模量和应变率的函数关系，方便分析应变率效应对约束再生混凝土初始弹性模量的影响规律.

(5)

(6)

式中：Ec表示受压初始弹性模量；εc为再生混凝土应变；εc0表示准静态受压峰值应变，根据试验结果，取值为1.97×10-3；其他模型参数取值见表4和6.

根据公式 (5)和相关模型参数，重新标定和分析约束再生混凝土受压初始弹性模量.表8给出非约束再生混凝土初始弹性模量计算结果.图14给出了不同应变率(10-5～10-2s-1) 下取代率为100%的受压初始弹性模量曲线分布情况.由表中的数据和图中曲线可以看出，随着应变率的提高，约束再生混凝土受压初始弹性模量随之增大.

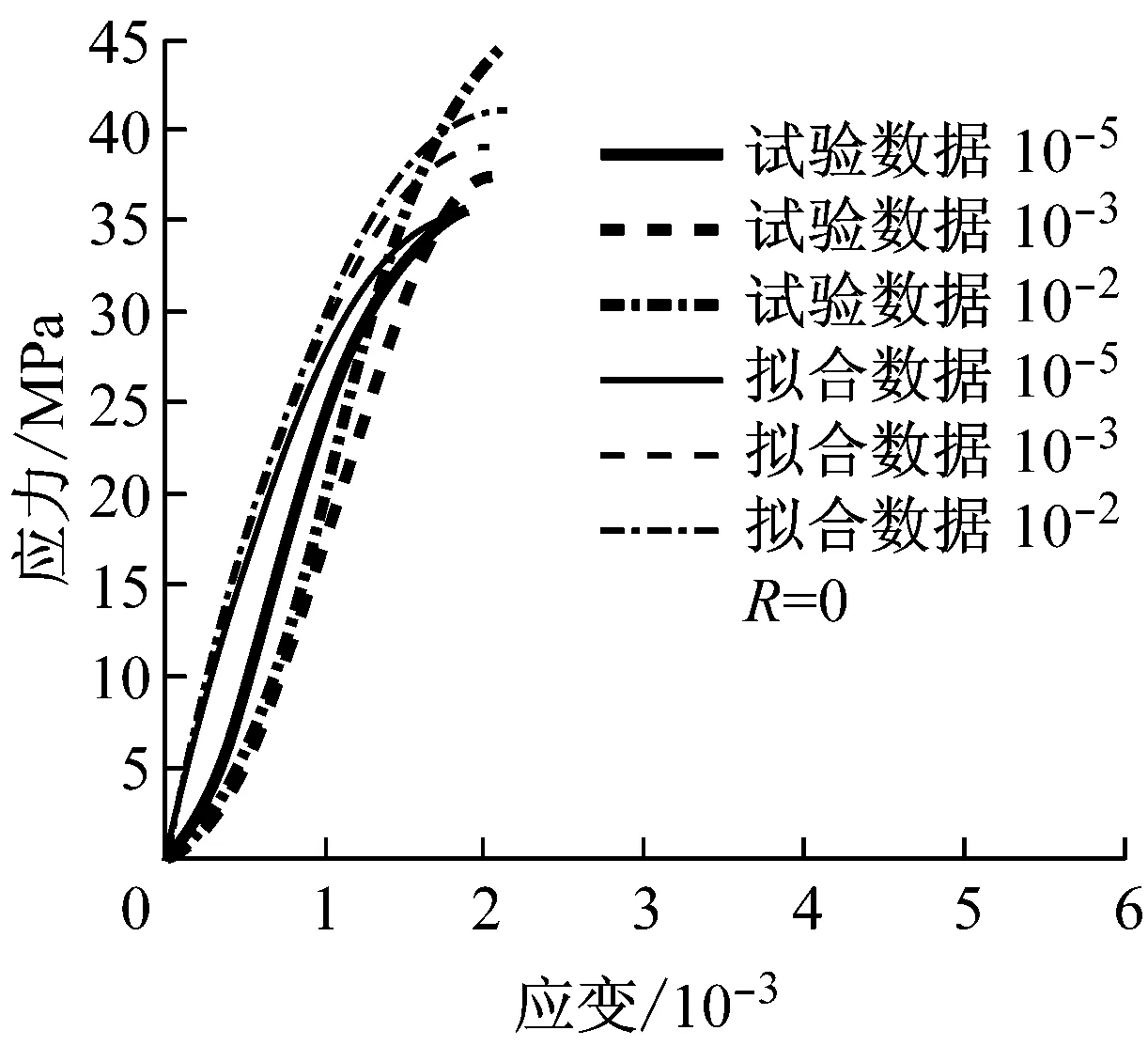
a R=0

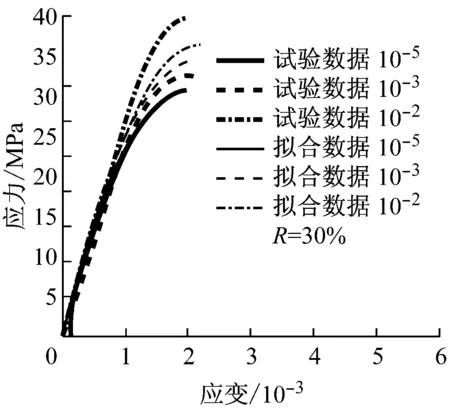
b R=30%

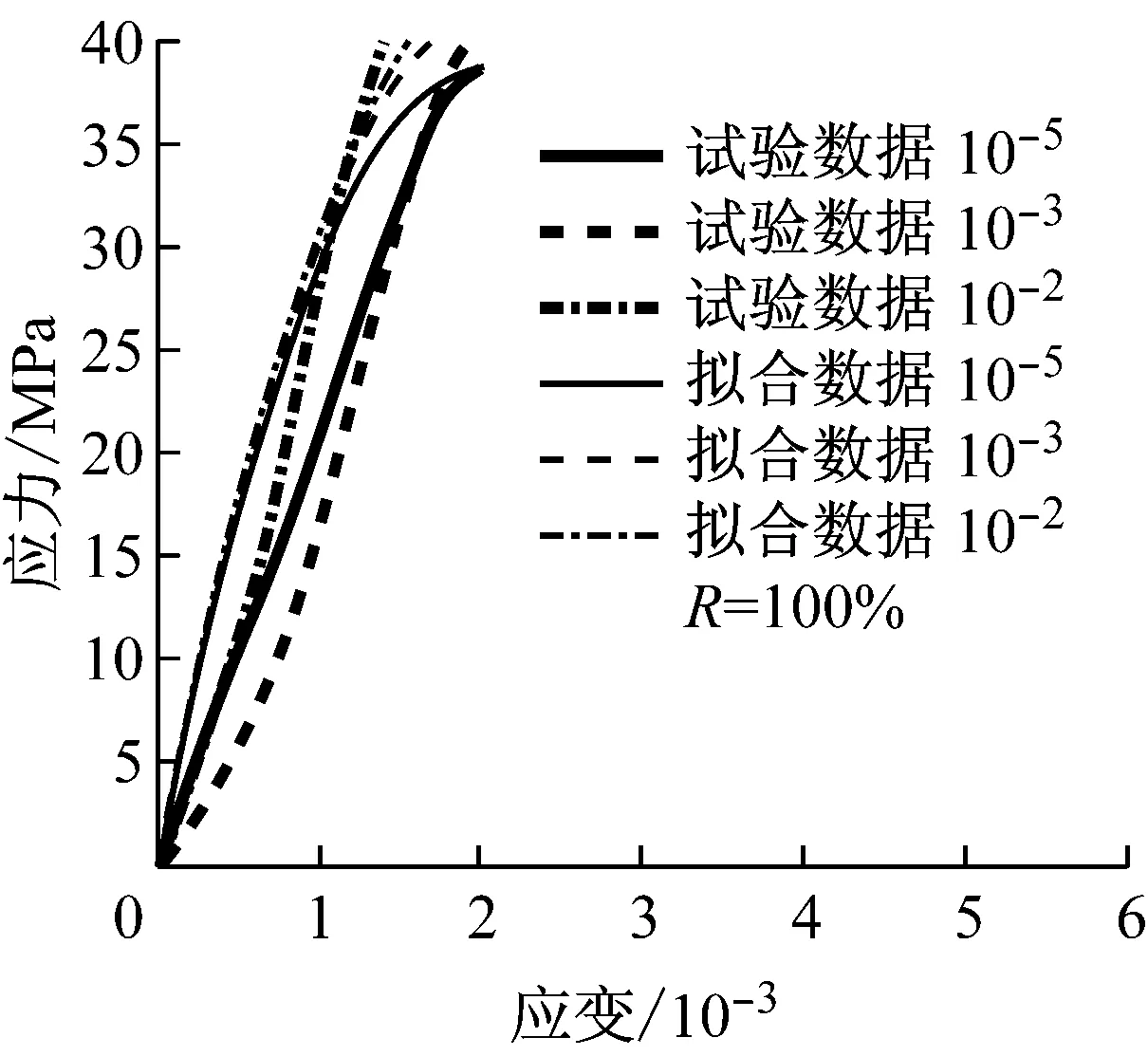
c R=100%

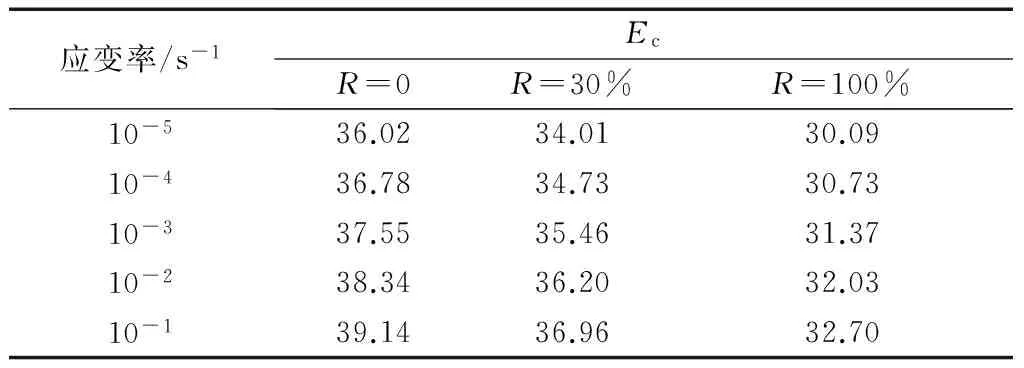
GPa

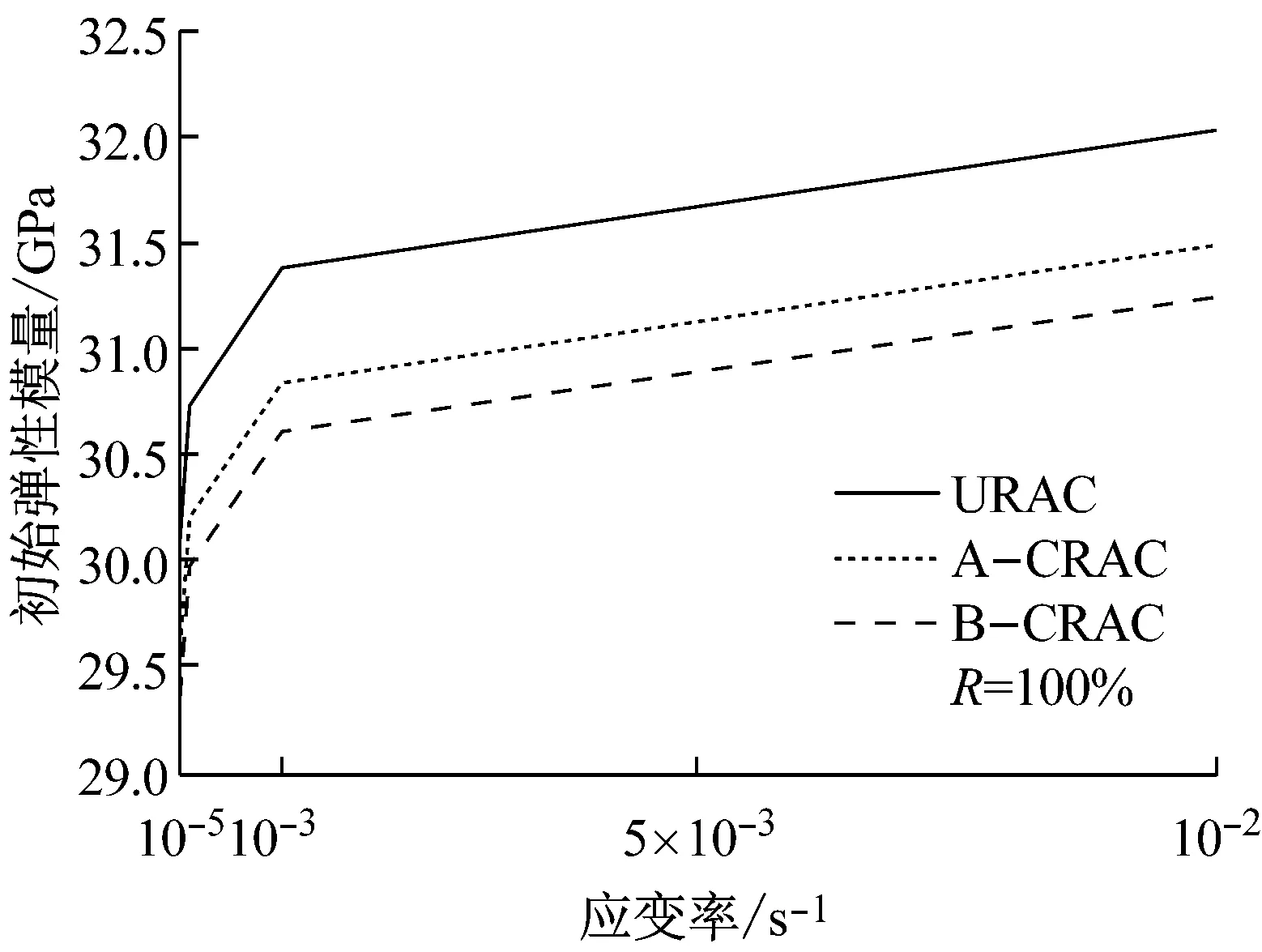
图14　约束再生混凝土受压初始弹性模量分布

为了进一步定量描述弹性模量增长幅值随应变率的变化规律，基于表8中的数据，对约束再生混凝土受压初始弹性模量的动态放大系数进行回归分析.初步提出受压初始弹性模量的动态放大系数函数模型，建议其数学关系表达式采用如下公式：

(7)

式中：kEc表示受压峰值应力动态放大系数；λ和κ均为函数模型参数，取值见表9.

通过公式(7)和表9中的数据，计算出不同应变率下量纲一化的约束再生混凝土初始弹性模量动态放大系数，如表10所示.不同应变率(10-5～10-1s-1) 下约束再生混凝土初始弹性模量动态放大系数的分布见图15.由表中的数据和图中的曲线可以看出，随着加载应变速率的提高，约束再生混凝土初始弹性模量动态放大系数随之增大，但其增长幅度要比受压峰值应力和峰值应变动态放大系数的小，这和大多数研究者所得到的结论是一致的[12-14].

表9　初始弹性模量动态放大系数函数模型参数

表10　量纲一化的初始弹性模量动态放大系数

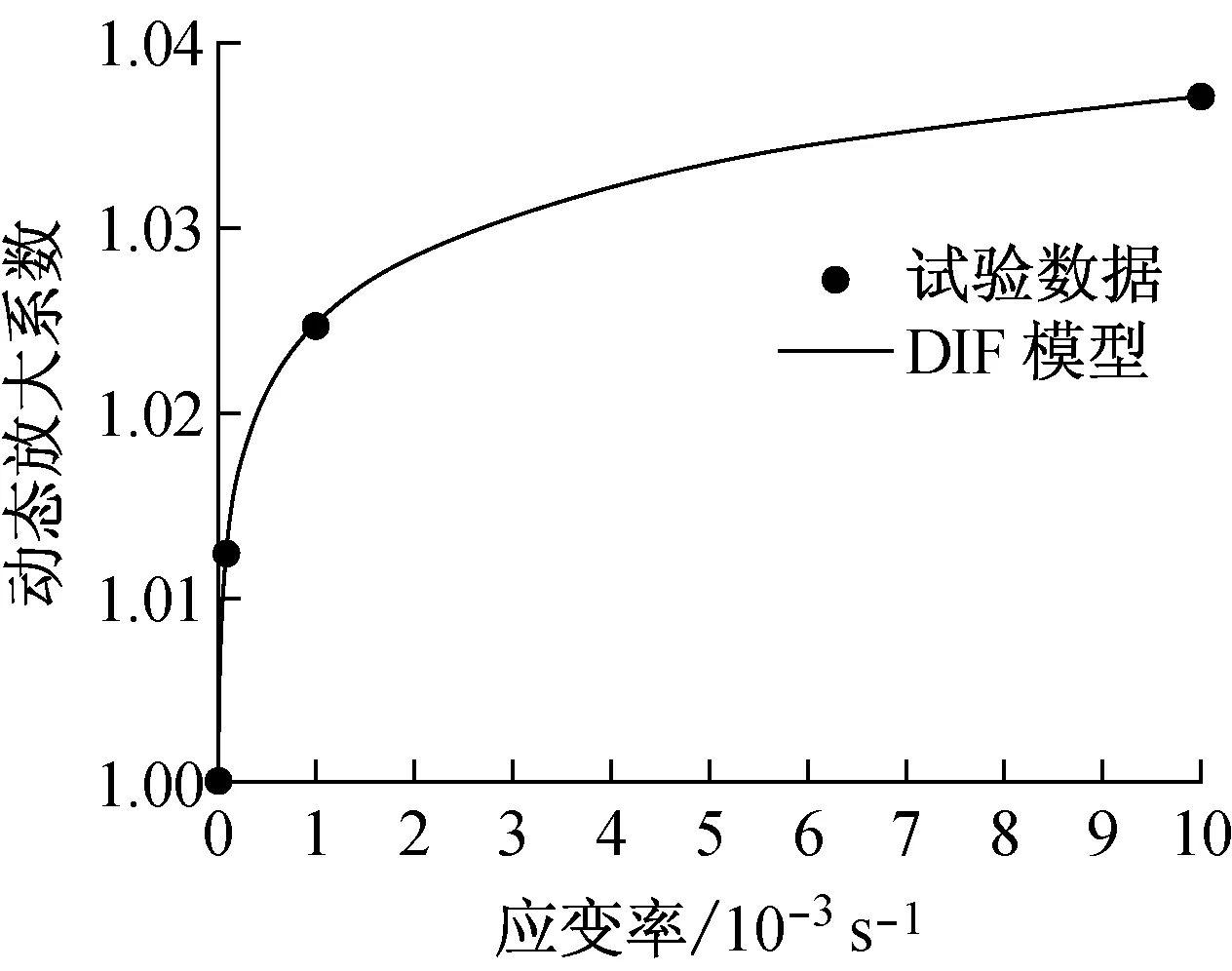
图15　约束再生混凝土初始弹性模量动态放大系数

4　结论

(1) 动力加载条件下的单轴受压单轴应力-应变关系曲线形状仍然符合经典单轴受压试验的基本描述.在不同应变率、再生粗骨料取代率或体积配箍率下，再生混凝土单轴应力-应变关系曲线的上升段基本一致，而下降段差异较为明显，随着应变率的提高或再生粗骨料取代率的增加，下降段曲线随之变陡.

(2) 随着加载应变率的提高，再生混凝土受压峰值应力随之增大.通过试验数据回归分析，提出约束再生混凝土受压峰值应力动态放大系数函数模型.

(3) 随着加载应变速率的提高，再生混凝土受压峰值应变动态放大系数随之增大，但其增加幅值低于受压峰值应力动态放大系数的增加幅值.提出约束再生混凝土受压峰值应变动态放大系数函数模型.

(4) 不同配箍率下，单轴应力-应变关系曲线的上升段基本一致，而下降段差异较为明显，随着箍筋配箍率的提高，下降段曲线明显随之趋于平缓.

(5) 确定了初始弹性模量和应变率的函数关系，分析了应变率效应对再生混凝土初始弹性模量的影响规律.提出受压初始弹性模量的动态放大系数函数模型，随着加载应变速率的提高，约束再生混凝土初始弹性模量动态放大系数随之增大，但其增长幅度要比受压峰值应力和峰值应变动态放大系数的小.

(6) 本文中以应变率为主要控制参数，在再生粗骨料取代率和体积配箍率均相同条件下，着重分析应变率大小对再生混凝土力学性能参数的影响规律，而有关再生粗骨料取代率和箍筋约束对再生混凝土动态力学性能的影响，以及约束再生混凝土本构关系，仍需今后进一步研究.

[1]Bischoff H, Perry S H. Compressive behaviour of concrete at high strain rates [J]. Materials and Structures, 1991, 24(6): 425.

[2]Abrams D A. Effect of rate of application of load on the compressive strength of concrete [J]. Journal of American Society for Testing and Materials, 1917, 17: 364.

[3]The Euro-International Committee for Concrete (CEB). CEB-FIP model code 1990 [S]. Lausanne: Thomas Telford Ltd, 1993.

[4]Hansen T C. Recycled aggregate and recycled aggregate concrete, second state-of-the-art report, developments from 1945-1985 [J]. Materials and Structures, 1986(111): 201.

[5]ACI Committee 555. Removal and reuse of hardened concrete [J]. ACI Material Journal, 2002, 99(3): 300.

[6]Xiao J Z, Li J B, Zhang C H. Mechanical properties of recycled aggregate concrete under uniaxial loading [J]. Cement and Concrete Research, 2005, 35: 1187.

[7]Xiao J Z, Li L, Shen L M,etal. Compressive behaviour of recycled aggregate concrete under impact loading [J]. Cement and Concrete Research, 2015, 71:46.

[8]Dilger W H, Koch R, Kowalczyk R. Ductility of plain and confined concrete under different strain rates [J]. ACI Journal, 1984, 81(1):73.

[9]闫东明, 林皋. 混凝土单轴动态压缩特性试验研究 [J].水利学与工程技术, 2005(6): 8.

YAN Dongming, LIN Gao. Experimental study on the uniaxial dynamic compression properties of concrete[J]. Water Sciences and Engineering Technology, 2005(6):8.

[10]Rostasy F S, Hartwich K. Compressive strength and deformation of steel fiber reinforced concrete under high rate of strain [J]. International Journal of Cement Composites and Lightweight Concrete, 1985, 7(1): 21.

[11]曾莎洁, 李杰. 混凝土单轴受压动力全曲线试验研究 [J]. 同济大学学报:自然科学版, 2013, 41(1):7.

ZENG Shajie, LI Jie. Experimental study on uniaxial compression behavior of concrete under dynamic loading [J]. Journal of Tongji University: Natural Science, 2013, 41(1):7.

[12]Takeda J, Tachikawa H. The mechanical properties of several kinds of concrete at compressive, tensile, and flexural tests in high rates of loading [J].Transactions of the Architectural Institute of Japan, 1962, 77:1.

[13]Mainstone R J. Properties of materials at high rates of straining or loading [J]. Materials and Structures, 1975, 8(44):102.

[14]肖诗云, 林皋, 逯静洲, 等.应变率对混凝土抗压特性的影响 [J]. 哈尔滨建筑大学学报, 2002, 35(5):35.

XIAO Shiyun, LIN Gao, LU Jingzhou,etal. Effect of strain rate on dynamic behavior of concrete in compression [J]. Journal of Harbin University of Civil Engineering and Architecture, 2002, 35(5): 35.

Influence of Strain Rate Effect on Mechanical Behavior of Recycled Aggregate Concrete

WANG Changqing1, 2, 3, XIAO Jianzhuang1, SUN Zhenping3

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. School of Civil Engineering and Architecture, Nanyang Normal University, Nanyan 473000, China; 3. School of Materials Science and Engineering, Tongji University, Shanghai 200092, China)

Based on uniaxial compressive dynamic mechanical experimental tests of confined recycled aggregate concrete (CRAC), the influence of strain rate effect on mechanical performance of CRAC was comprehensively investigated. The dynamic failure pattern and the experimental complete curves of uniaxial compressive stress-strain of RAC subjected to dynamic loading with different strain rates were analyzed. It is found that for the uniaxial CRAC curves of strain-strain relationship, at various strain rates, replacement ratios of recycled coarse aggregate (RCA) or volume stirrup ratios, the feature of the ascending branch is basically consistent. However, the descending branch exhibits some differences. With the increase of the strain rate or the replacement ratio of RCA, the descending branch changes in a steepening trend. However, with the increase of the volume stirrup ratio, the descending branch changes obviously in a flattening trend. Through regression analysis of experimental test data, models of the dynamic increase factor (DIF) for the compressive peak stress and the peak strain were proposed, respectively. With increasing amplitude of strain rate, the compressive peak stress and peak strain of CRAC increases. However, the increasing trend of DIF for the compressive peak strain is smaller than that of the compressive peak stress. The influence of strain rate on the initial elastic modulus of CRAC was also investigated, and the relationship between the initial elastic modulus and the strain rate was determined based on the experimental data. Furthermore, the model of the DIF of the initial elastic modulus of CRAC was established. It is concluded that the DIF of the initial elastic modulus of CRAC increases at dynamic loading with increasing amplitude of strain rate, however, the increasing trend is smaller than that of the compressive peak stress, as well as that of the compressive peak strain.

recycled aggregate concrete; confined; dynamic tests; strain rate effect; mechanical behavior; dynamic increase factor

2015-10-30

中国博士后科学基金(2014M550247,2015T80449);国家自然科学基金(51438007);河南省重点科技攻关项目(152102310027)

王长青(1981—),男,博士后,主要研究方向为再生混凝土动态力学性能.E-mail:c.q.wang@foxmail.com

肖建庄(1968—),男,教授,博士生导师,工学博士,主要研究方向为再生混凝土材料与结构.E-mail:jzx@tongji.edu.cn

TU528.79；TU317.1

A