福建海坛湾波流双向耦合下水动力特征

匡翠萍， 王彬谕， 顾　杰， 雷　刚

(1.同济大学 土木工程学院，上海 200092；2.广西交通职业技术学院，广西 南宁 530216；3. 上海海洋大学 海洋科学学院，上海 201306；4.国家海洋局第三海洋研究所，福建 厦门 361005)



福建海坛湾波流双向耦合下水动力特征

匡翠萍1， 王彬谕2， 顾杰3， 雷刚4

(1.同济大学 土木工程学院，上海 200092；2.广西交通职业技术学院，广西 南宁 530216；3. 上海海洋大学 海洋科学学院，上海 201306；4.国家海洋局第三海洋研究所，福建 厦门 361005)

采用MIKE 21软件中SW(spectral wave)波浪模块和FM(flow model)潮流模块，将潮流模块计算得到的水位与流速输入波浪模型，将波浪模块计算得到的辐射应力输入潮流模型，建立海坛湾波流双向耦合的水动力数学模型.分别计算纯潮流和纯波浪作用下的潮流场和波浪场，计算结果与实测数据吻合良好，再分别对波流双向耦合作用下的潮流场和波浪场进行了模拟.比较结果表明：波流耦合作用对流速和波高都有一定的影响；在波流异向特性明显的区域，波高增大显著；涨落急时刻波高在近岸区域的衰减速率和纯波浪作用下的较一致；落急时刻波高开始显著衰减的位置明显早于涨急时刻；波浪辐射应力在破碎带附近对流速的影响最大.

海坛湾； 波浪； 潮流； 波流耦合; MIKE 21

海洋中潮流与波浪总是共存的，它们相互作用下波流二者均发生一定的变化.一方面波浪的存在对潮流产生影响，如流速分布发生变化；另一方面潮流也影响着波浪的动力特性，如波浪要素发生变化等.波浪和潮流的共同作用影响着河口海岸区域诸多物理现象，如泥沙输移、岸滩演变和建筑物周围的冲淤等.因此，研究波流共同作用比研究单纯的波浪或水流更具有现实意义.Li[1]，Malarkey和Davies[2]采用势流理论对波流边界层结构进行研究；Davies等[3]对波流共同作用下边界层内与层外的流场结构进行研究.吴永胜等[4]在波流边界层模型的基础上利用k-ε方程联合求解边界层内外波流运动.孙昭晨和王世澎[5]通过数值模拟指出波浪在长时间作用后，波浪辐射应力对潮位的影响很小，但对潮流流速有比较大的影响.

平潭县位于福建省东部海域，东临台湾海峡，西临海坛海峡(图1)，由海坛岛等126个岛屿和近千个岩礁组成，主岛海坛岛为全国第五大岛，是福建省第一大岛.海坛湾是一个半封闭海湾，湾口朝向正东方向，湾内岛屿众多，地形复杂，大部分水深在7～20 m之间，波浪潮流相互作用显著[6].目前对该区域水动力环境的数值研究尚在起步阶段.汤军健等[7]采用二维浅水方程模拟了海坛海峡的前进波性质.杜凌等[8]采用三维有限元模型模拟了台湾海峡的潮汐和潮流特征，结果表明最大理论潮差出现在海峡西北部的海坛岛至兴化湾一带.刘浩等[9]运用二维河口海岸动力模型模拟了福清湾潮汐潮流的基本特征.田永青和潘爱军[10]基于统计方法和潮汐调和分析方法给出了台湾海峡西部近海的潮汐时空分布特征及其变化规律.林航[11]基于福建三沙湾内近一年的实测逐时潮位资料计算分析了各站潮位特征值.刘涛等[12]应用抛物型缓坡方程、Boussinesq方程建立了福建兴化湾波浪数学模型，计算得到了兴化湾深水区域以及工程区域的设计波浪要素.叶雨颖等[13]对现场测得的一个月的风浪过程资料进行了统计分析和频谱分析，给出了福建省南部港湾-东山湾的波高和周期分布，特征波要素与频谱关系.张军等[14]采用波浪模拟的方法计算得出福建沿海海域波浪能资源分布状况.栾曙光等[15]对在福建省中部登陆的台风引起的台风浪过程进行了数值模拟计算，总结出闽中近岸西北行路径台风浪的波向变化规律.

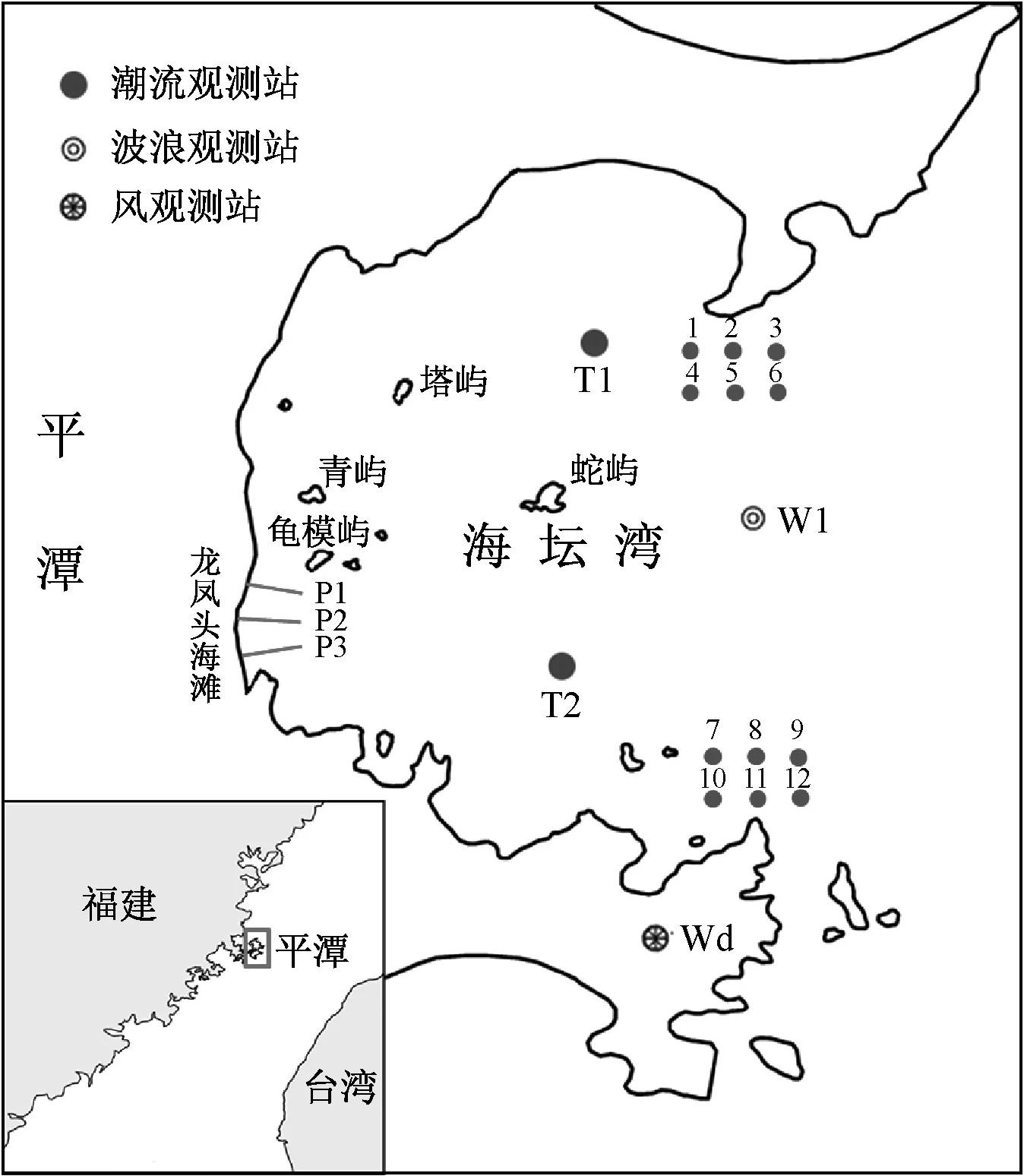
图1　海坛湾地理位置及测站、剖面布置

Fig.1Location of Haitan Bay and observation stations and profiles

2009年，平潭县建立福州平潭综合实验区，2010年正式更名为福建省平潭综合实验区.目前实验区结合平潭岛东部海岸的自然条件、景观特色和历史基础，致力于将海坛湾滨海沙滩创造为国内一流的高质量的旅游、休闲、娱乐海滩.因此有必要建立波流双向耦合作用下数学模型研究该区域的水动力特性，为海坛湾滨海沙滩修复提供科学支持.

1　数学模型

1.1潮流模型

MIKE 21 FM(flow model)模块在对二维非恒定流进行模拟的同时还可考虑密度变化、水下地形、潮汐变化和气象条件等，同时采用无结构三角网格，适用于模拟具有复杂边界的海岸和河口环境，并能进行干、湿单元的设置，能较方便地进行涨落潮过程中滩地干、湿交替的情况.在笛卡尔直角坐标系下，通过对水平动量方程与连续方程的积分而得到如下二维浅水方程[16]：

(1)

(2)

(3)

式中：t为时间；x,y为笛卡尔坐标系坐标；η为水位；d为静水水深；h=η+d为总水深；u,v分别为x,y方向的水深平均流速；f=2Ωsinφ为科氏力系数(Ω为地球自转角速率，φ为地理纬度)；g为重力加速度；ρ为水的密度；τbx,τby分别为x,y方向上的底床剪切力；τsx,τsy分别为x,y方向上的表面风应力.Txx,Txy,Tyy为水平黏滞应力项，可以根据沿水深平均的速度梯度用涡流黏性方程得出

(4)

水平涡黏性系数A由Samagorinsky公式确定

(5)

其中：cs为一常数，在本文中取0.28；l为特征长度；Sij为变形率

(6)

Sxx,Sxy,Syy为波浪辐射应力分量，是波浪模型和水流模型实现耦合的关键部分，波浪辐射应力表达式为

(7)

式中：E为波能，E=ρgH2/8；θ为波向；n=cg/c，其中c为波速，cg为波群速度大小，且

(8)

式中：k为波数矢量，k=(kx，ky)；σ为相对角频率.

1.2波浪模型

MIKE 21 SW(spectral wave)是基于波浪作用平衡方程的谱波浪模型.该模型能够很好地描述波浪在近岸的传播过程，不仅能够考虑由于地形变化引起的波浪浅水变形和折射，而且考虑了风区内风成浪和由于底部摩阻及波浪破碎所引起的能量耗散.此外，它还能模拟波浪在水流作用下的传播. 在笛卡尔坐标系下，模型的控制方程为[17]

(9)

(10)

(11)

(12)

(13)

式中：U为流速，U=(u，v)；s为沿波浪θ方向的空间坐标；m为垂直于s的坐标.

方程(9)左边第一项代表波能随时间的变化；第二项代表波能随地理空间、频率空间和波向空间的变化.右边项S=Sin+Snl+Sds+Sbot+Ssurf代表使方程能量守恒的源项;Sin为风输入的能量,Snl为波与波之间的非线性作用引起的能量损耗,Sds为由白帽引起的能量损耗,Sbot为底部摩阻引起的能量损耗,Ssurf为由于水深变化引起的波浪破碎产生的能量损耗[17-18].

1.3耦合模型实现过程

首先模拟得到在风作用下的潮流场和波浪场；然后将潮流模型中计算得到的水位与流速输入波浪模型，得到新的波浪参数，同时将波浪模型中计算得到的辐射应力输入到潮流模型，得到新的水位、流速(图2)，两个模型时间步长和计算时间一致，以此方式交换数据实现双向耦合；最后进行比较分析，得到波浪和潮流耦合作用下的水位、流速和波高变化.

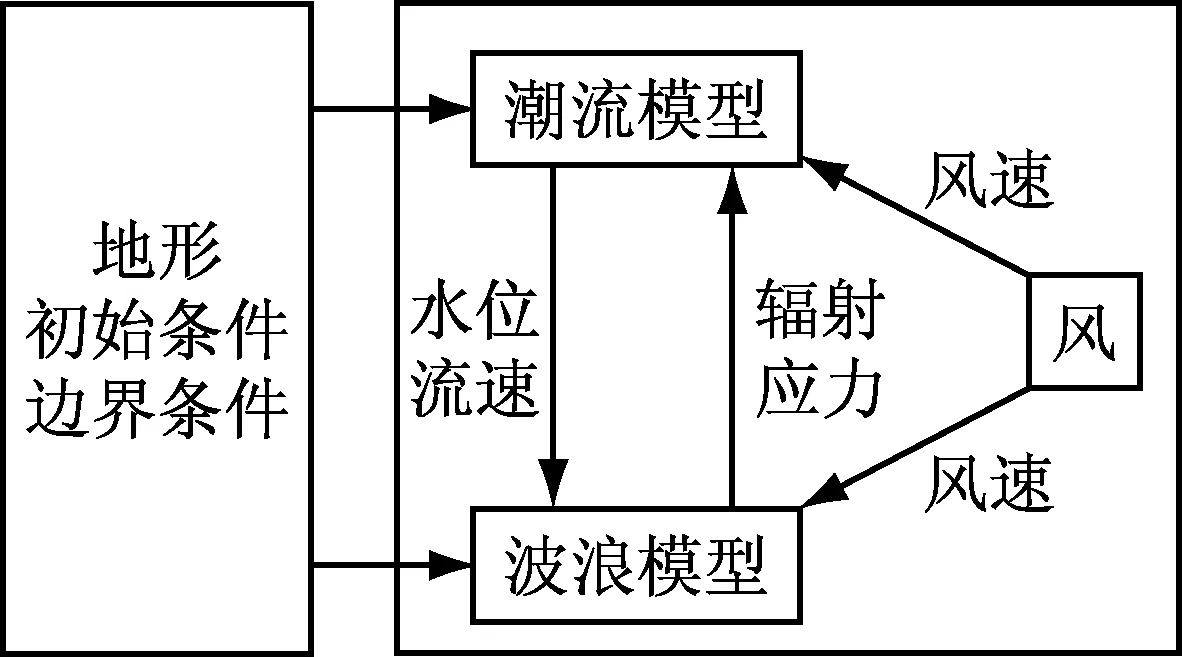
图2　波流耦合模型中变量传递示意图

Fig.2Schematic of variable transfer in wave-current coupled model

2　计算区域及模型验证

2.1计算区域

模型计算范围覆盖平潭东部海域(图3)，由一条陆边界和北、东、南三条开边界包围；采用三角形网格进行剖分，共有8 701个节点和16 593个单元.开边界网格较为稀疏，最大空间步长可达1 000 m；海坛湾内进行了网格加密，根据网格敏感性测试，网格空间步长在10～30 m，计算结果相差小于3%，因此加密网格的空间步长取20 m.

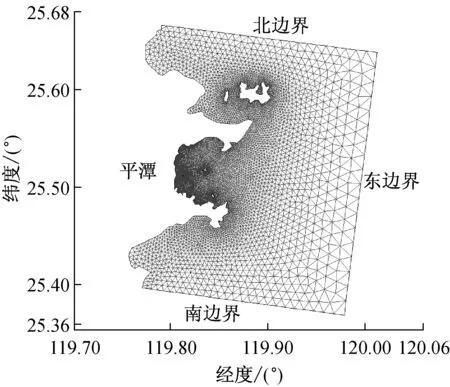
图3　计算网格

2.2边界条件及参数选取

潮流模型三条开边界以潮位作为驱动力，水位过程由验证后的台湾海峡大模型提供[19].初始潮位选取计算开始时刻的平均潮位，初始流速为零.由于存在潮滩，落潮干出，涨潮被淹，因此采用动边界模拟.干水深hdry、淹没水深hflood和湿水深hwet分别取0.005 m,0.05 m和0.1 m.当hhflood时，只计算连续性方程，动量方程不参与计算；当h>hwet时，连续性方程和动量方程都参与计算.鉴于海坛湾床面泥沙以黏土质粉砂和中细砂为主，泥沙中值粒径一般小于0.5 mm，即泥沙粒径较细，床面糙率kn采用推荐值0.001 m，曼宁数M先根据其与床面糙率kn和水深h分布关系进行赋值，经模型率定后取为30～50 m1/3·s-1.在保证计算稳定的条件下，采用变化计算时间步长1～30 s来提高计算效率.

入射波浪来源于平潭波浪观测站(图1)实测波浪的统计分析：春、夏、秋、冬四季常浪向均为ENE向；春季平均有效波高为1.25 m，平均波周期为4.1 s；夏季平均有效波高为1 m，平均波周期为4 s；秋季平均有效波高为2 m，平均波周期为4.9 s；冬季平均有效波高为2.4 m，平均波周期为5.1 s.根据平潭风观测站(图1)统计的历史各月最多风向和平均风速：平潭海域受季风影响，风向季节性变化明显；一年中秋、冬、春三季以偏北风为主，夏季以偏南风为主，除6～8月的最多风向为SSW向以外，其余各月最多风向均为NNE向.春、夏、秋、冬四季平均风速分别为7.6，6.3，9.3和8.8 m·s-1.

模型将夏季平均波高与波周期、冬季平均波高与波周期分别作为常浪和强浪情况，设置两组从东边界入射的入射波(表1)，其中波向采用常浪向ENE向.风速及风向分别对应选取夏季和冬季平均风速和风向.波浪破碎采用Battjes和Janssen模型，破碎指标取0.8.根据龙凤头海域表层泥沙中值粒径，粗糙高度取平均值0.1 mm.

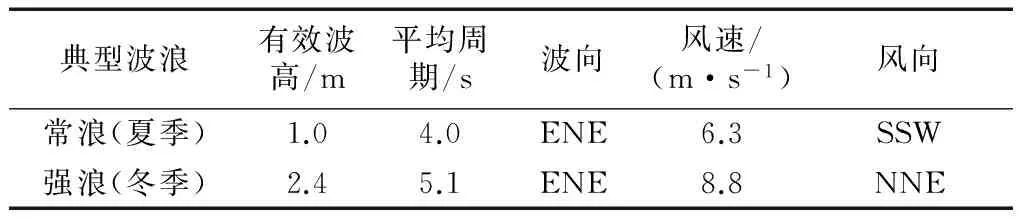
表1　典型波浪参数

2.3模型验证

平潭东部海域潮流模型基于海坛湾内T1和T2测流站(图1)一次天文大潮(2011年8月16日10时至8月17日12时)的实测垂向平均流速、流向及水深数据进行验证.图4为T2测流站水深、流速与流向的验证，可见模型计算的水深、潮流过程与实测变化趋势一致.本文选择比较常用的Wilmott[20]提出的统计学方法来评价数学模型，其计算方法为

(14)

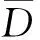
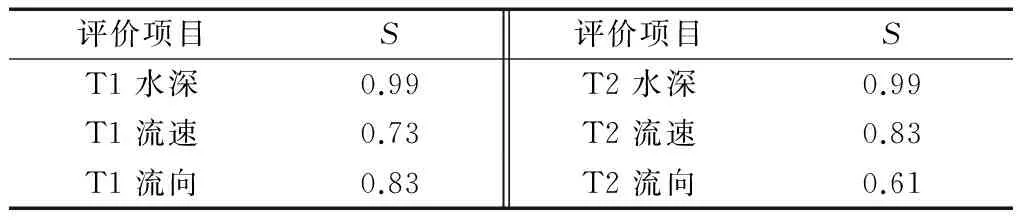
表2　模型效率系数

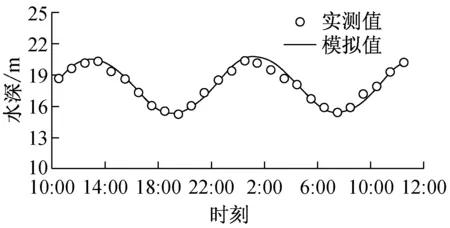
a 水深

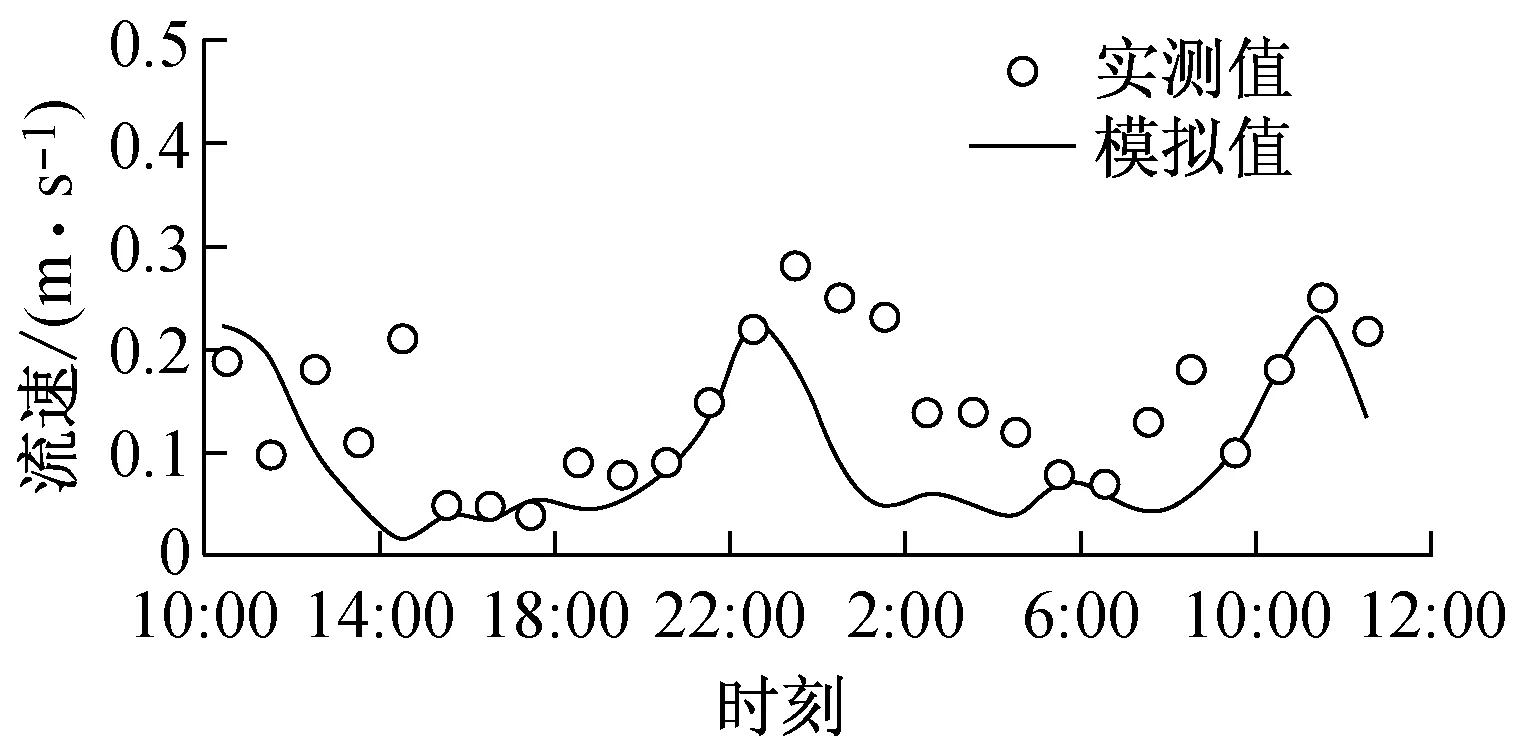
b 流速

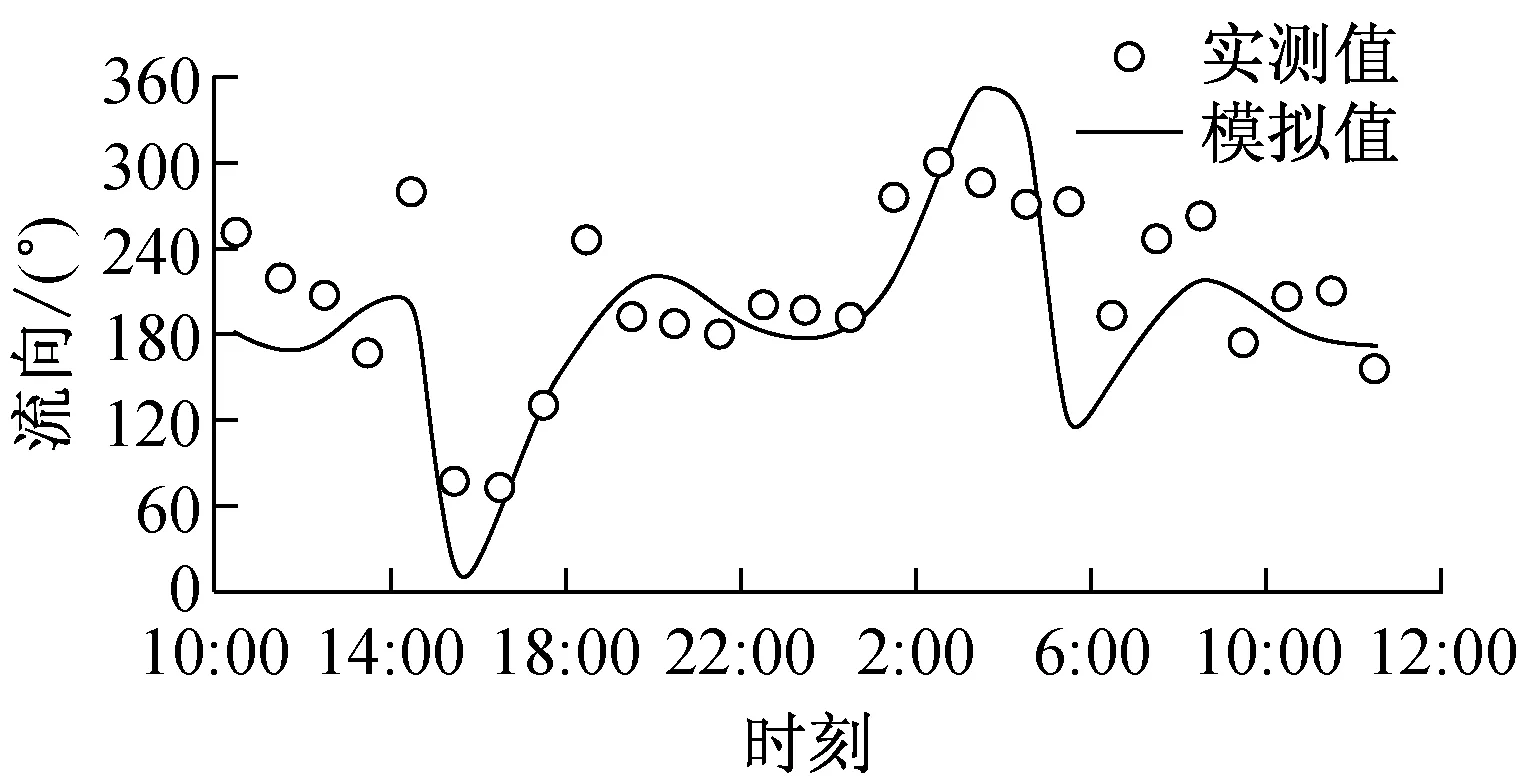
c 流向

图4T2测流站模型水深、流速和流向验证(2011-08-16 T10:00～2011-08-17 T12:00)

Fig.4Verification of water depth, flow velocity magnitude and direction (2011.8.16 10:00 to 8.17 12:00)

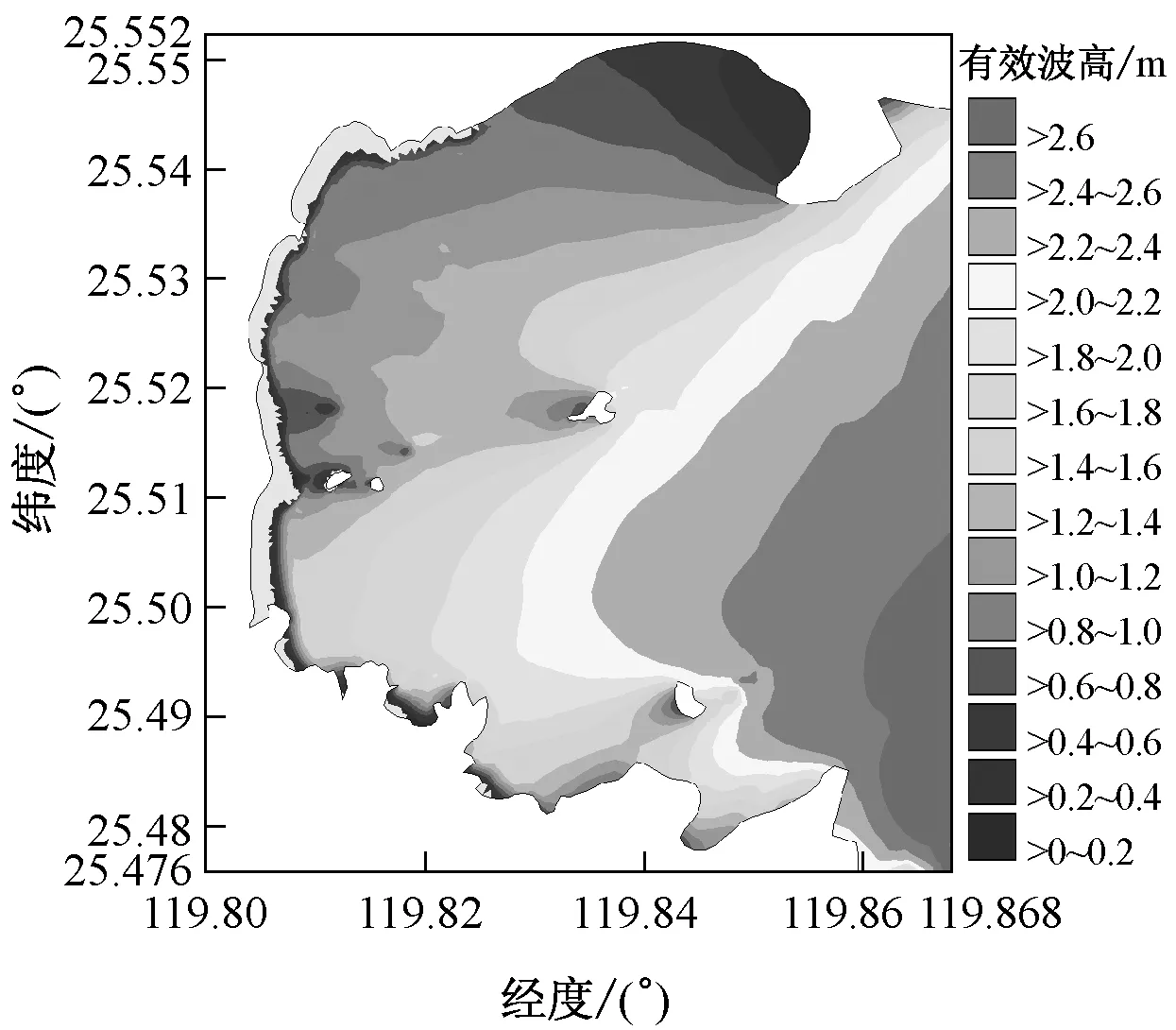
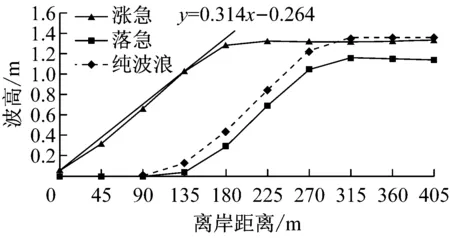
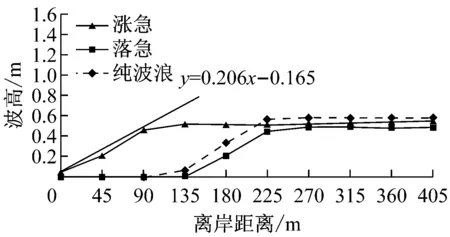
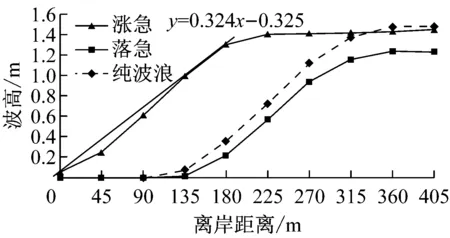
图5a和图6a分别为纯波浪作用时常浪和强浪两种情况下海坛湾内波高分布.从波浪场分布看，波浪在近岸区受地形、水深作用发生折射，波向线逐渐垂直于岸线方向；受波浪绕射作用影响，岛屿后侧波高削减显著.模拟结果与观测波浪数据统计结果均显示主波向为ENE方向.常浪时观测站实测波高和波周期分别为1.04 m和4.10 s，计算波高和波周期分别为1.00 m和4.20 s；强浪时观测站实测波高和波周期分别为2.40 m和5.10 s，计算波高和波周期分别为2.42 m和5.09 s，与观测数据吻合.

3　波流耦合结果分析

3.1海坛湾波流变化分析

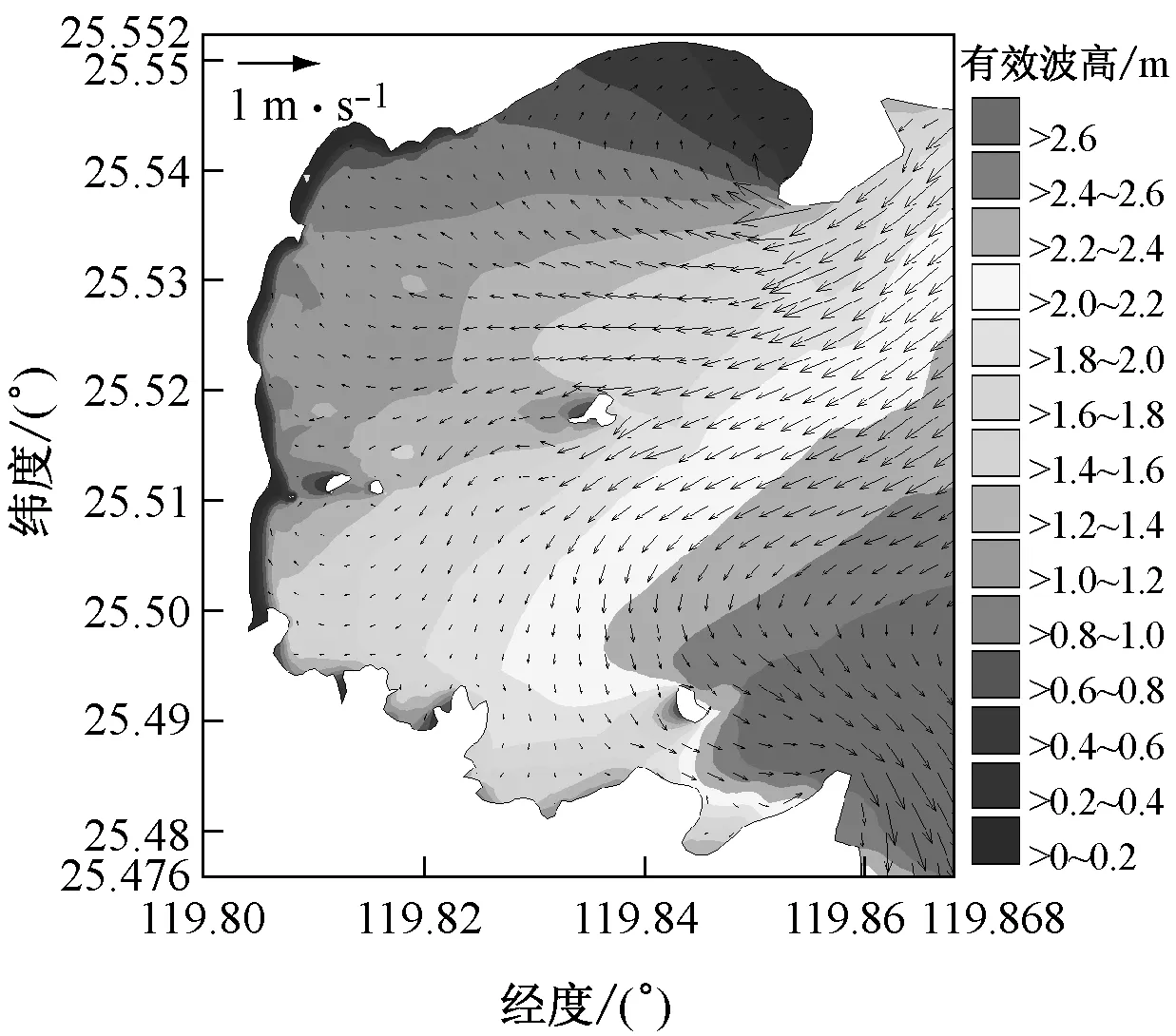
图5b，c和图6b，c中渐变色等值线分别代表常浪和强浪作用下海坛湾内波高分布，矢量代表海坛湾涨落急时刻的流场.可以看出：海坛湾内水流总体表现为往复流，湾口流速最大，湾内流速较小，湾顶流速最小.波流耦合作用时波高分布形态与纯波浪相比有一定差异：潮流作用较强且波流异向明显的区域，如湾口南北两端，潮流对波浪有较大的影响.涨急时刻，湾口南侧岬头处波流异向明显，波高明显增大，波高等值线密集且向湾内凸出；落急时刻，湾口北侧海域波流异向特征明显，波高明显大于其他海域.

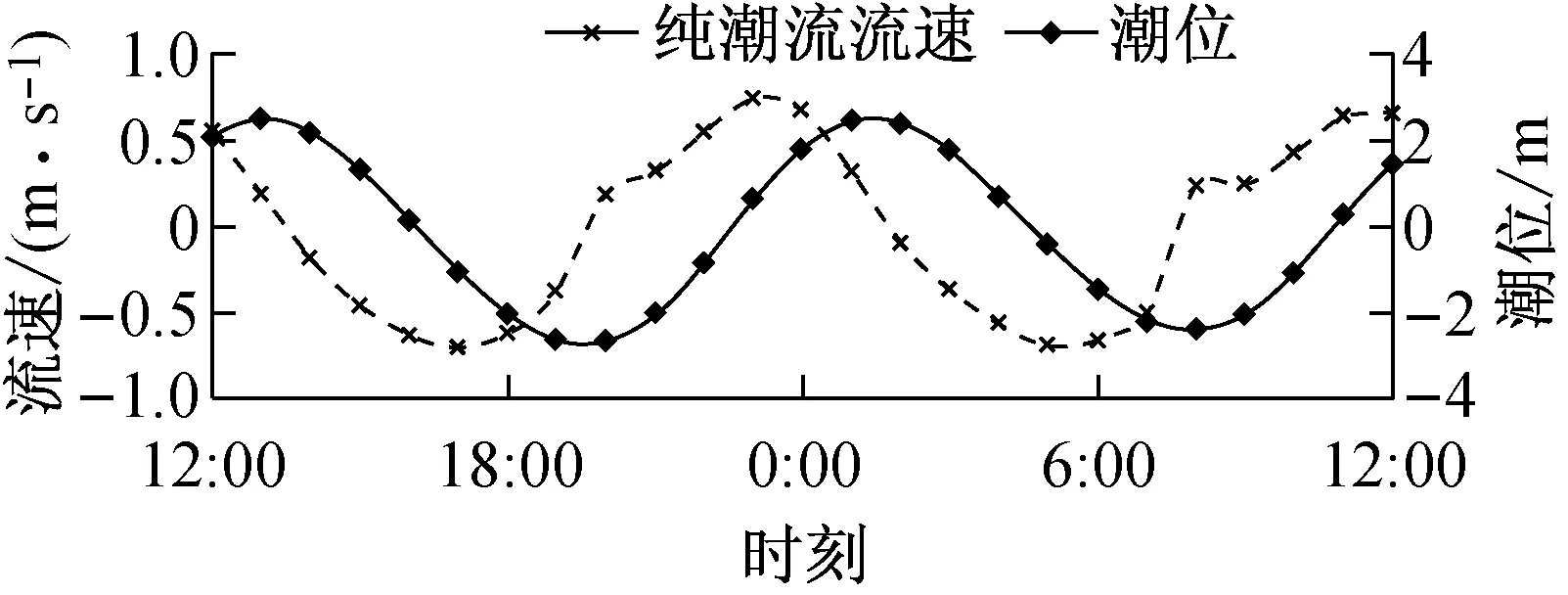
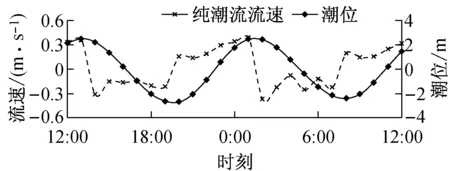
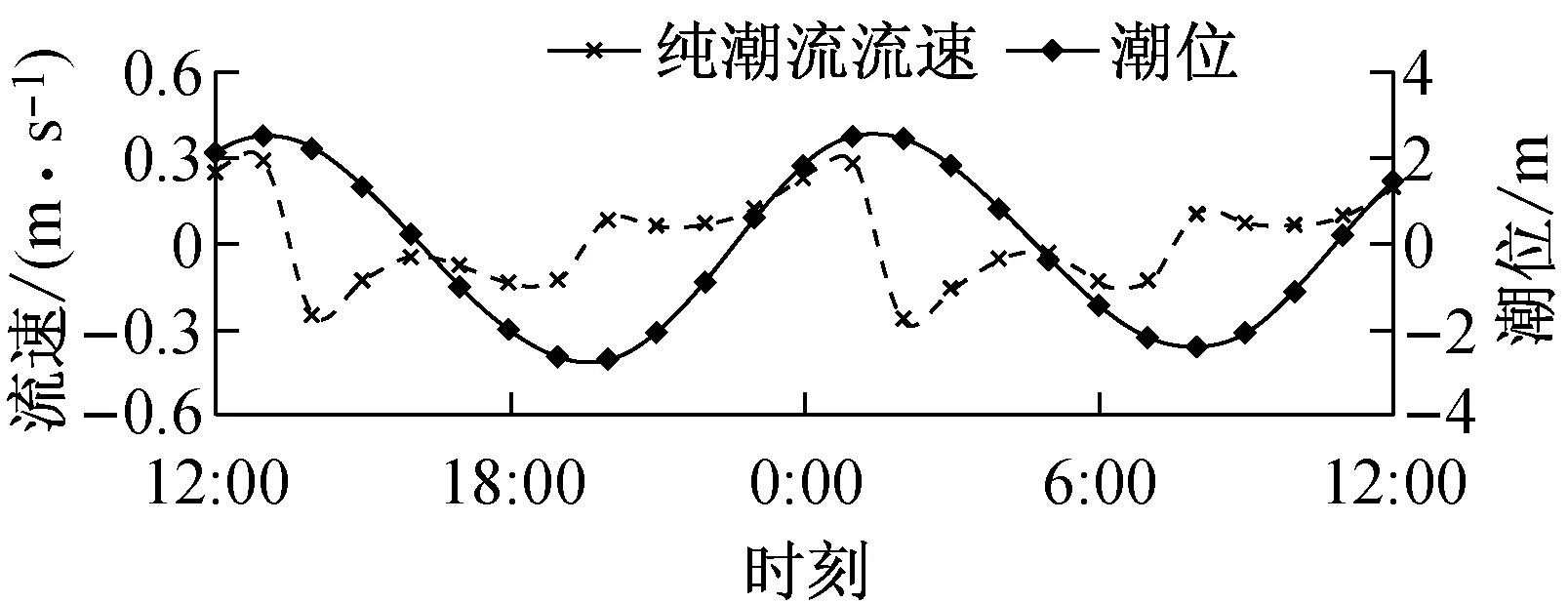
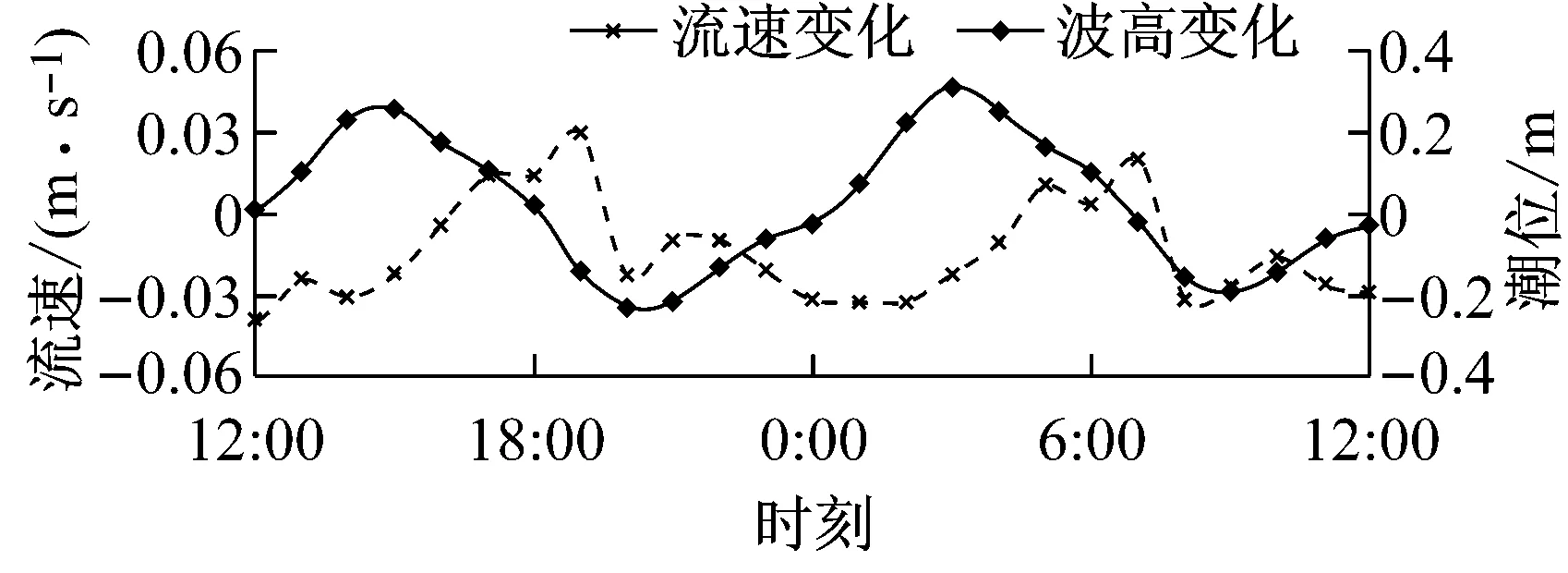
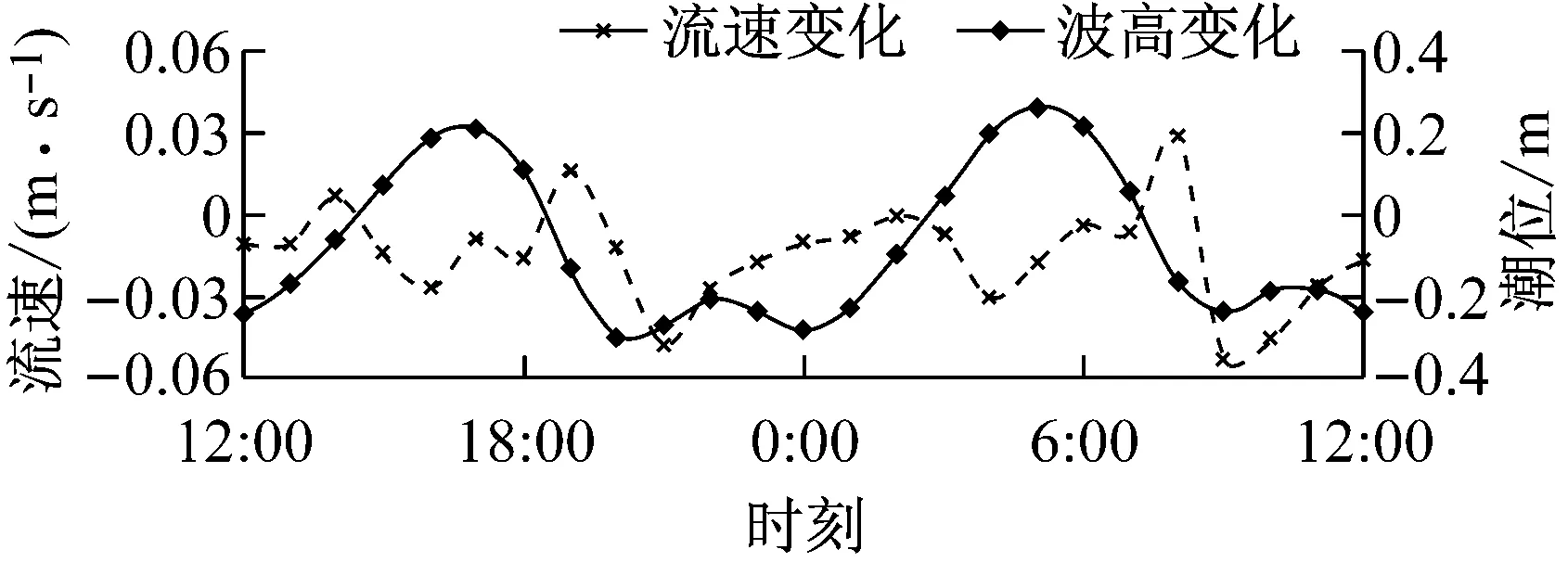
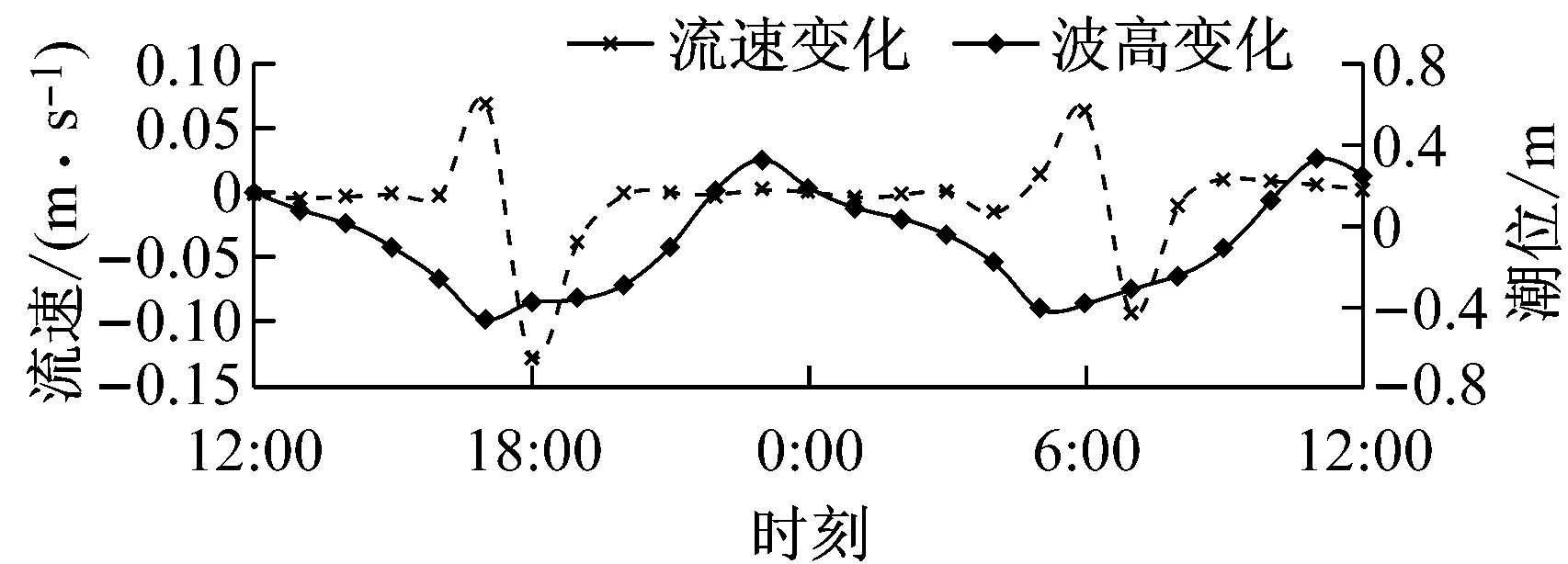
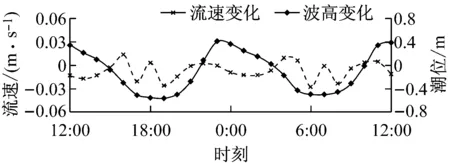
为了定量分析波流耦合作用对波高及流速的影响，在涨落急时刻流速较大且往复流特征明显的区域布置12个监测点(点1～12)，测点布置如图1所示.图7为纯潮流作用下点1，3，8和10的潮位和流速过程线(涨潮为正，落潮为负).图8为强浪作用下4个监测点的波高变化(强浪加流-纯波浪)和流速变化(流加强浪-纯潮流).结果表明：波流耦合作用对波高和流速都有较大影响.波流耦合作用下，波高过程线变化受潮波形态主导.波高变化和流速变化呈现一定的负相关关系，波向和水流流向相顺时，波高减小，流速增大；相逆时，波高增大，流速减小.比较图7和图8可知，波流耦合作用时流速大小变化幅度约为10%.

3.2近岸海域波流变化分析

波浪从深水传入浅水过程中，波高、波速及剖面形状都在不断发生改变，受水深变浅、水流作用以及风作用等的影响.本文以龙凤头海滩(福建平潭最佳海滨浴场之一)近岸海域作为研究对象，分析研究近岸海域波浪与水流双向耦合作用下的水动力特性.

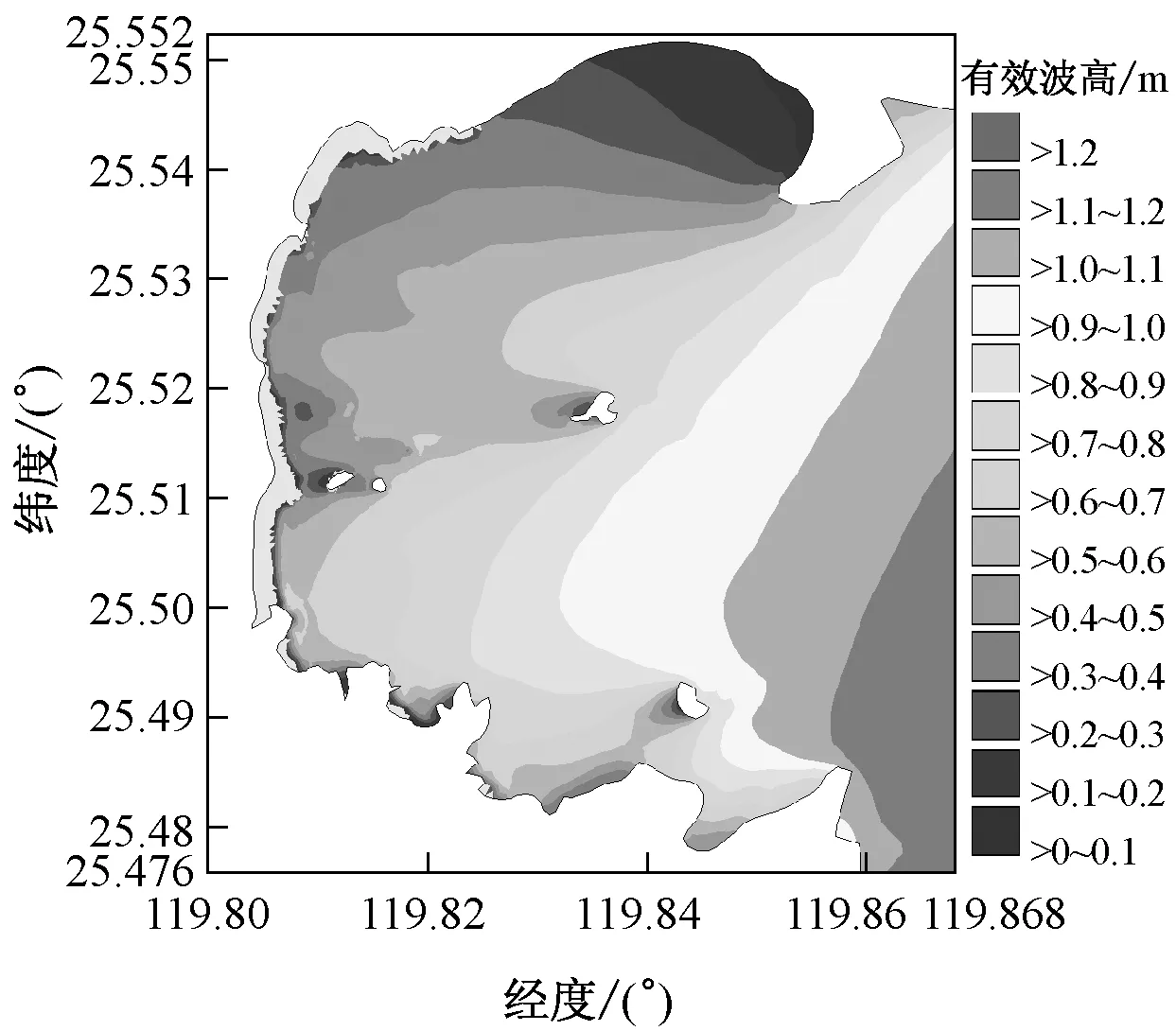
a 无潮流

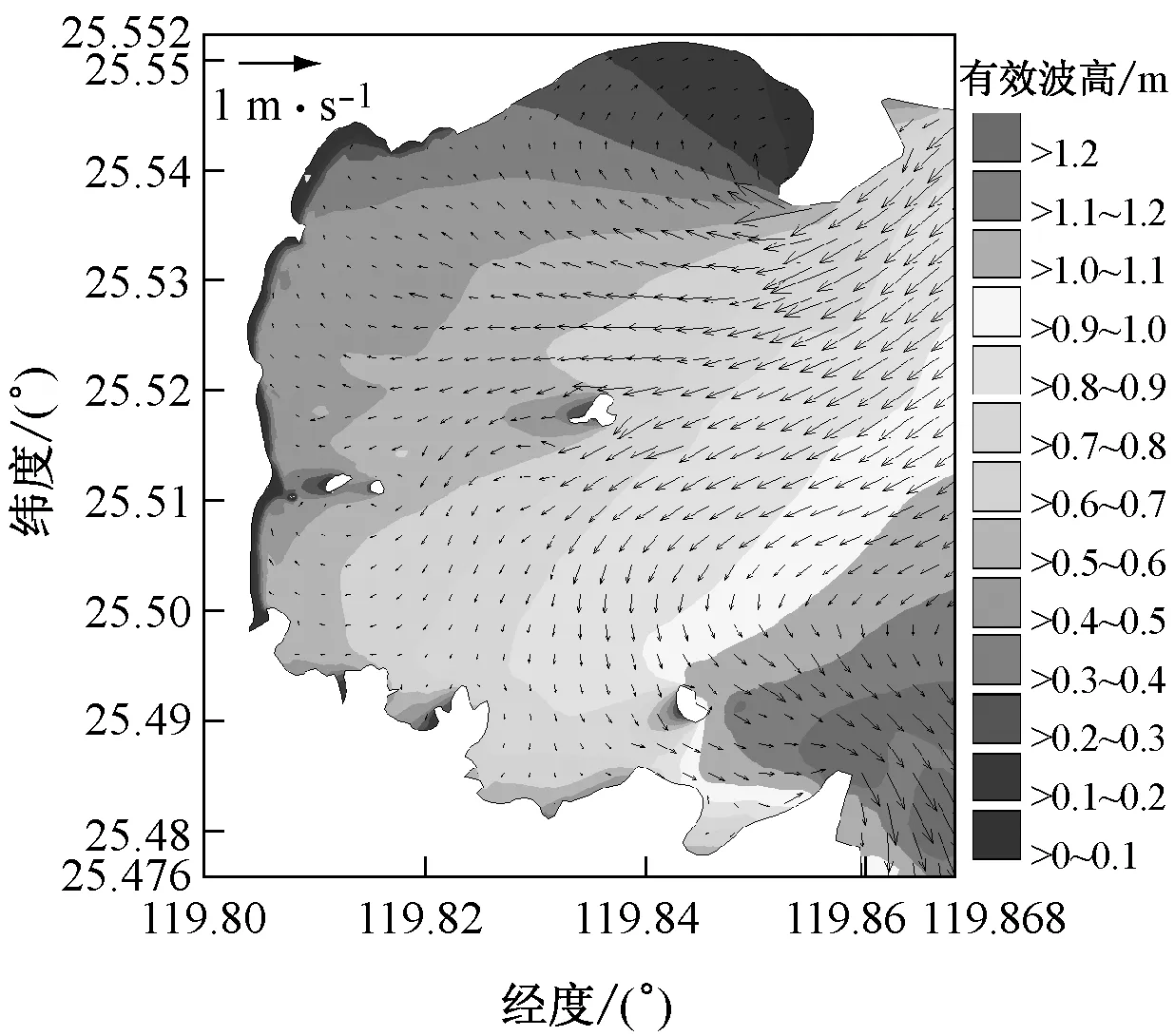
b 波流耦合下涨急时刻

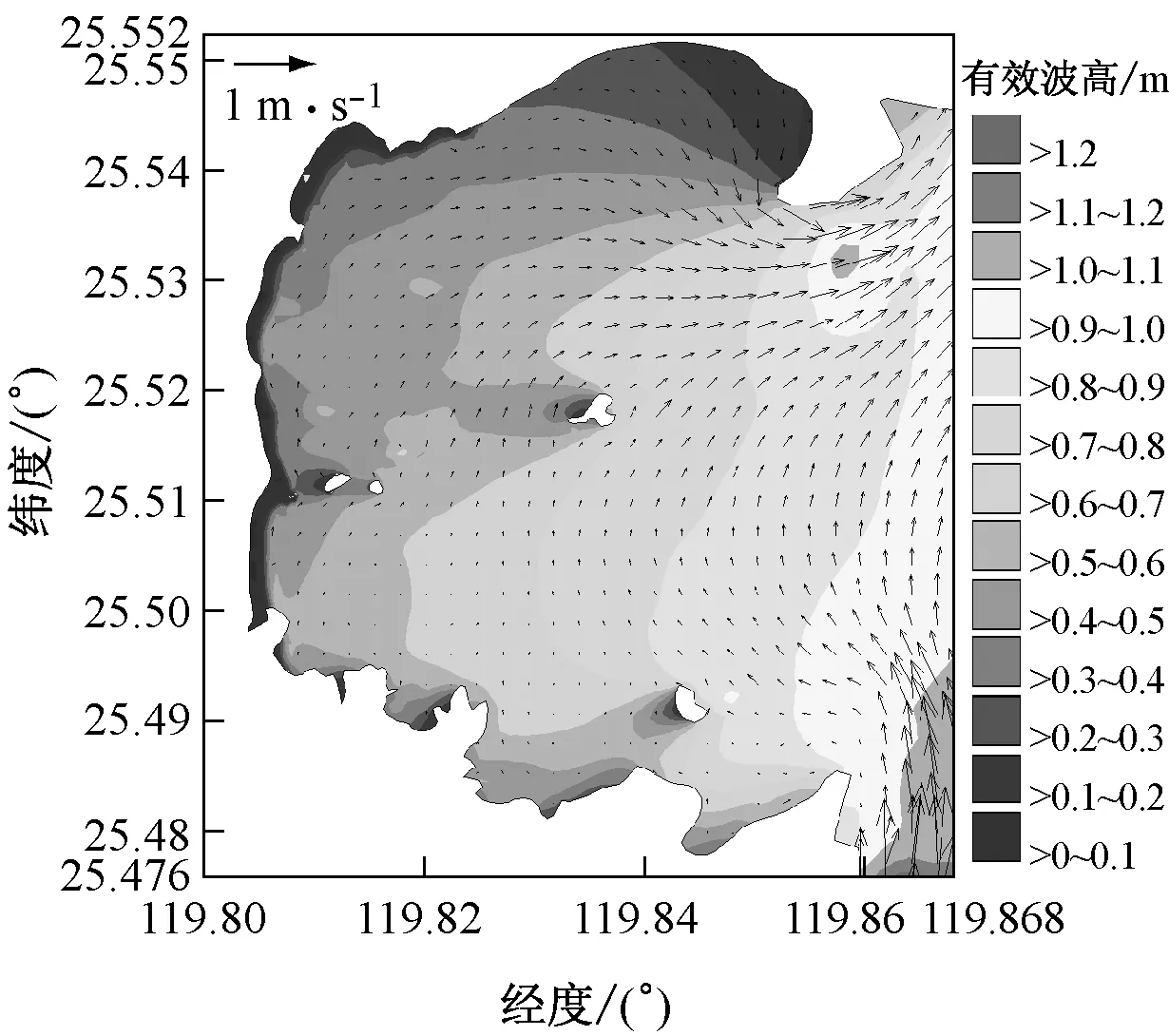
c 波流耦合下落急时刻

a 无潮流

b 波流耦合下涨急时刻

b 测点3

a 测点8

b 测点10

Fig.7Time history of tidal level and flow velocity (positive for flood current and negative for ebb current) under pure current condition

a 测点1

b 测点3

a 测点8

b 测点10

Fig.8Time history of wave height change (strong wave coupled with current-pure wave) and flow velocity (current coupled with strong wave-pure current)

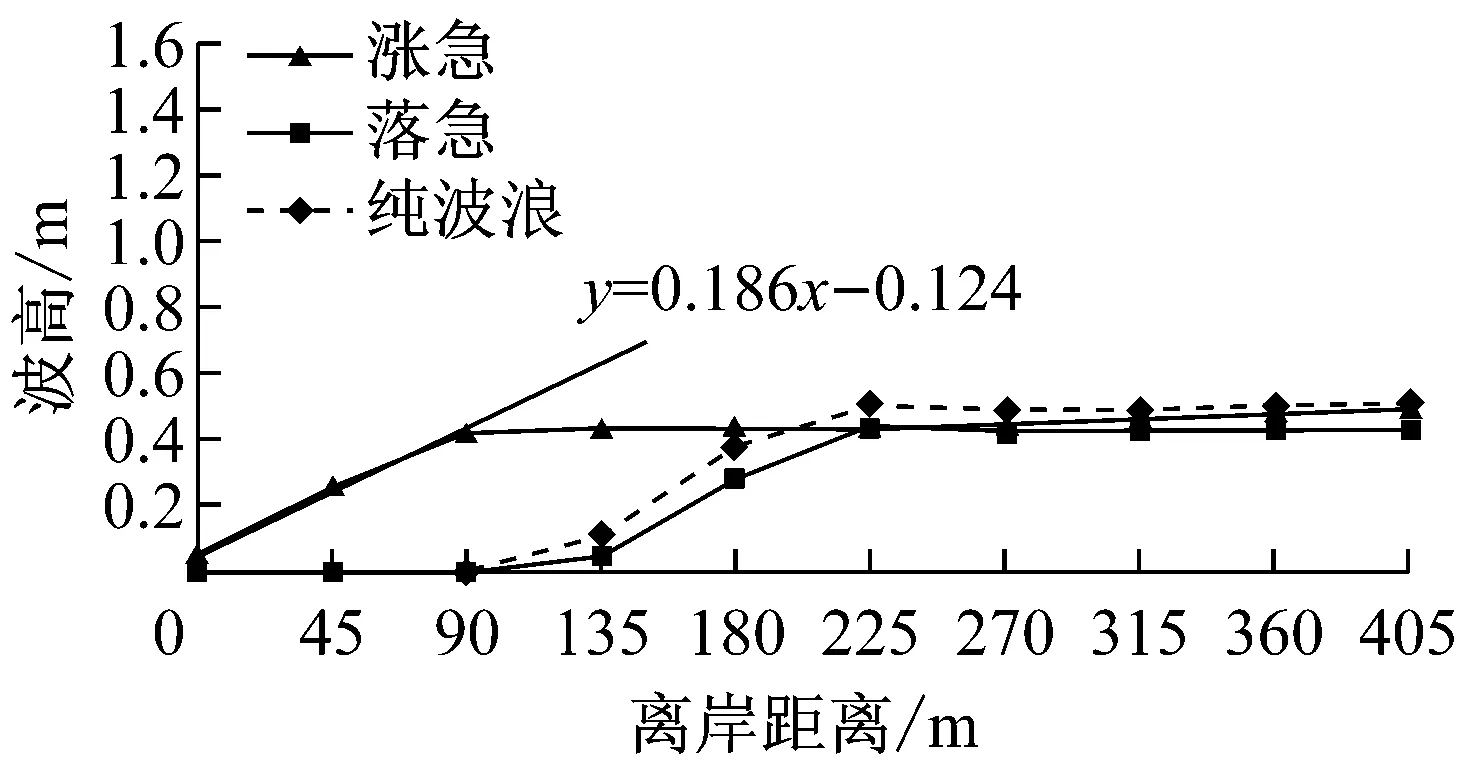
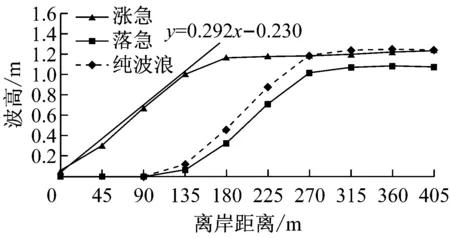
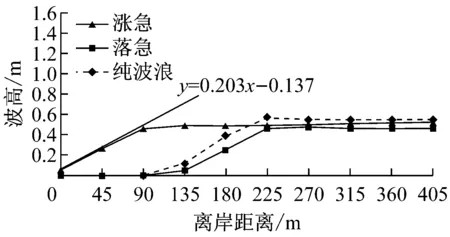
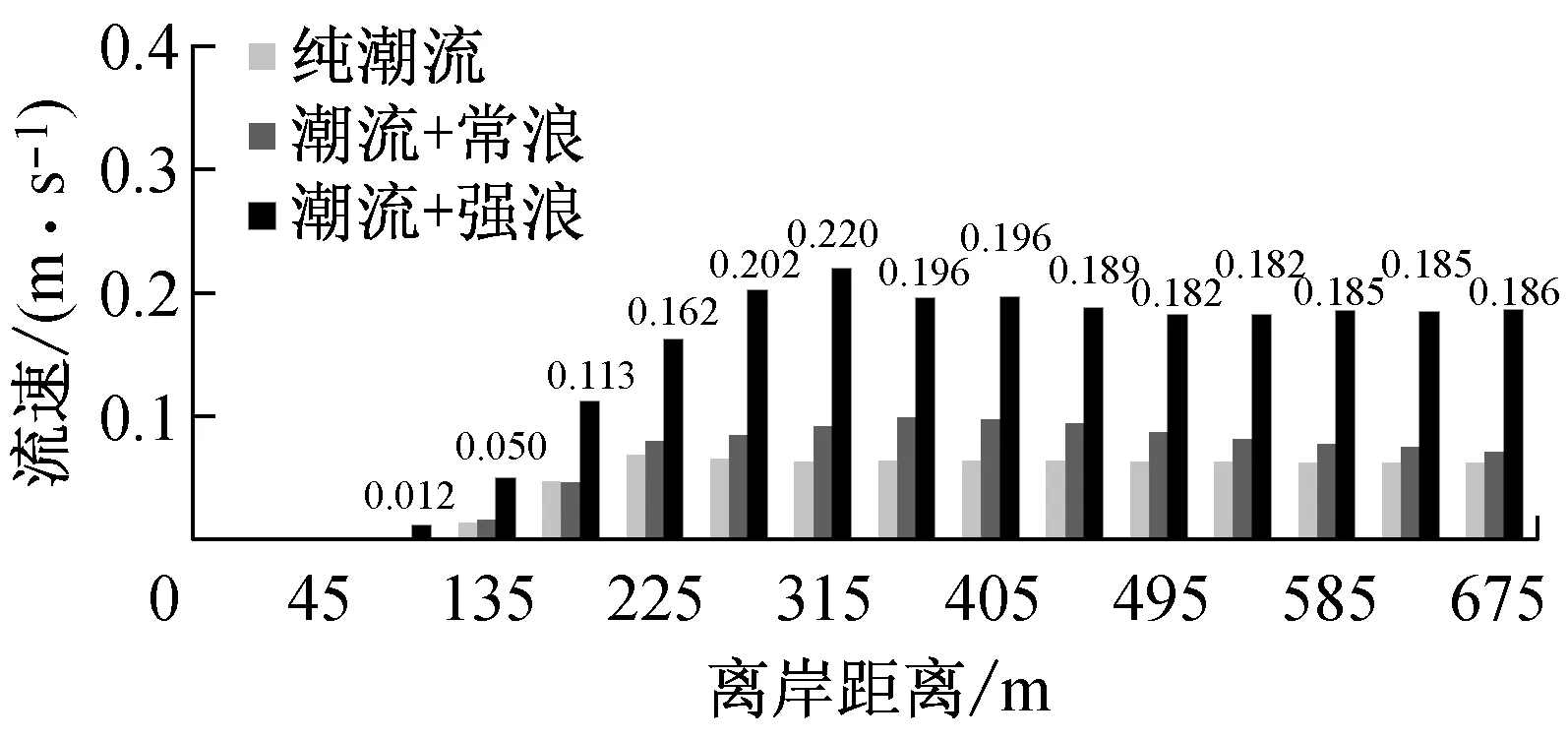
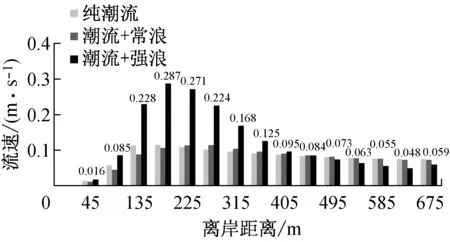
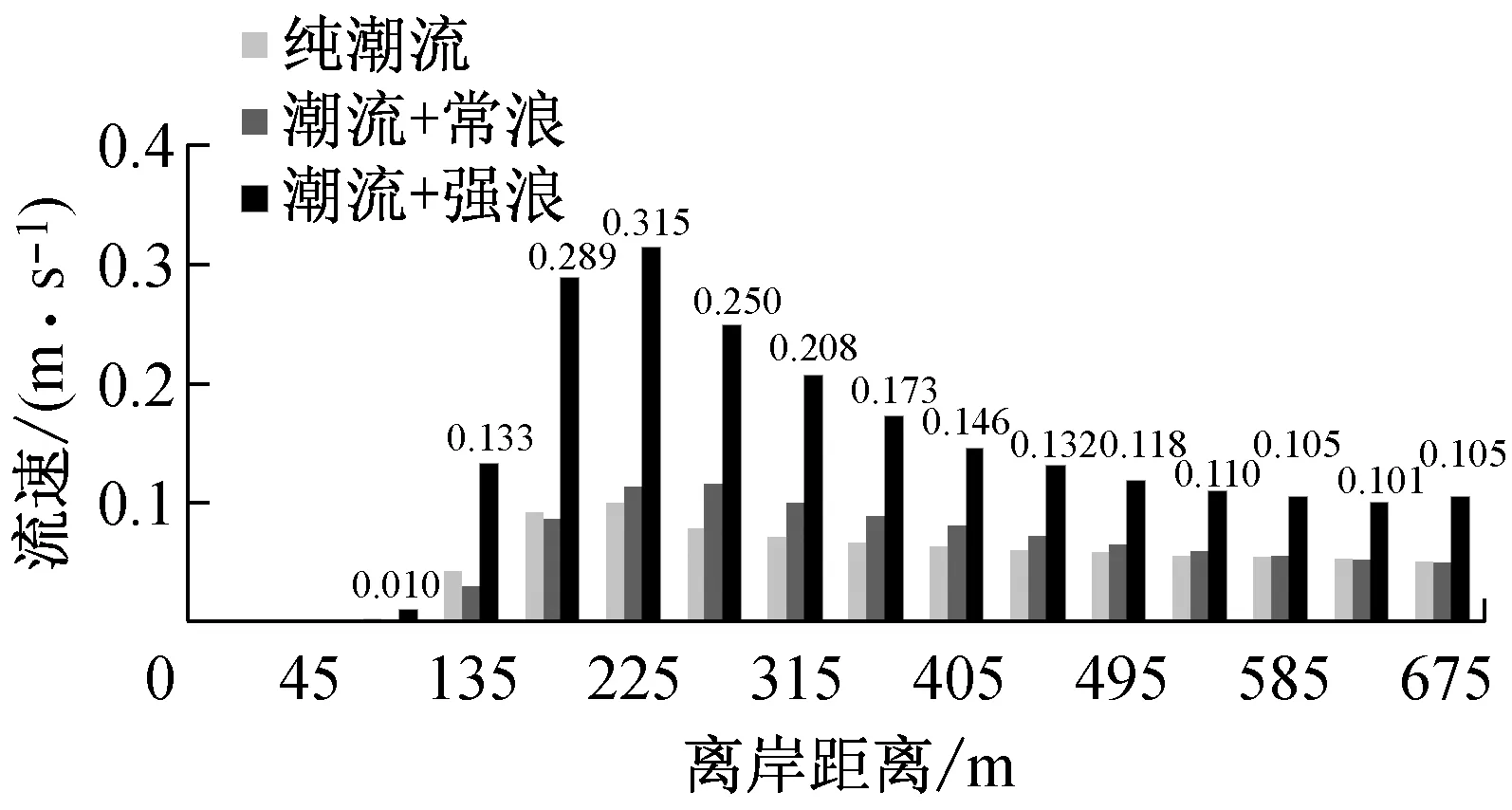
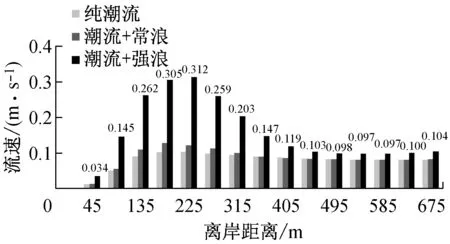
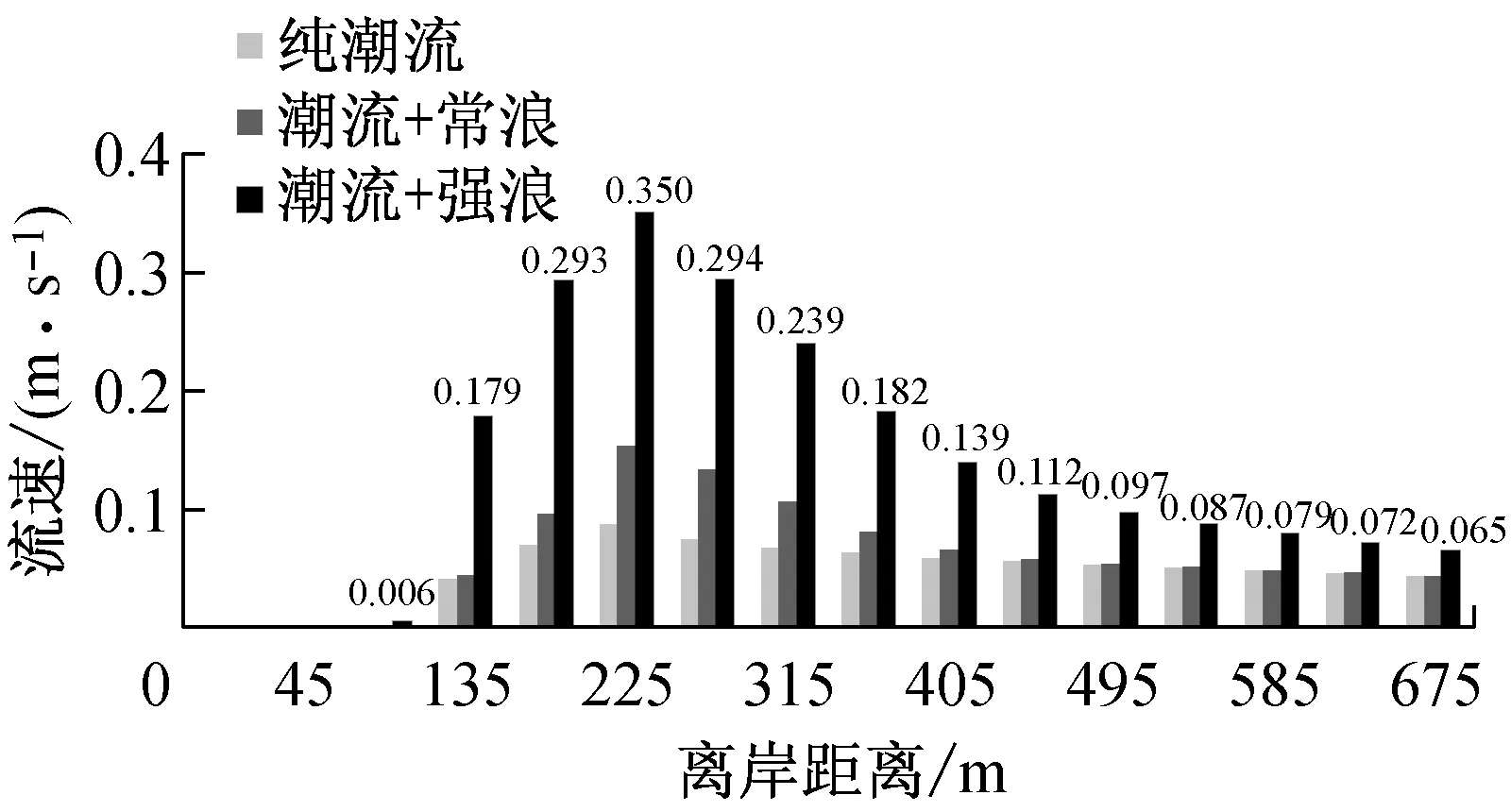
图9为常浪和强浪作用下近岸各剖面波高分布.由于涨急时刻近岸水深明显大于落急时刻，因此落急时刻波高开始显著衰减的位置明显早于涨急时刻，且入射波高越大，波高衰减位置越早.当入射波高为1 m时，涨落急时刻的衰减位置分别在离岸90 m和225 m；当入射波高为2.4 m时，涨落急时刻的衰减位置分别在离岸180 m和270 m.考虑波浪在浅水区域的衰减速率主要取决于底床坡度及沉积物特性，因此涨落急时刻波高在近岸区域的衰减速率和纯波浪作用下较一致，在常浪和强浪作用下，近岸波高衰减速率分别在0.2和0.3左右.在常浪和强浪作用下，当离岸距离分别大于225 m和315 m时，涨急时刻的波高与纯波浪作用下几乎一致，但均大于落急波高，且随入射波高的增大，波高差异也随之增大，当入射波高为2.4 m时，离岸区域(离岸距离超过315 m)涨急时刻的波高约为1.43 m，落急时刻的波高为1.23 m，两者相差约为0.2 m.

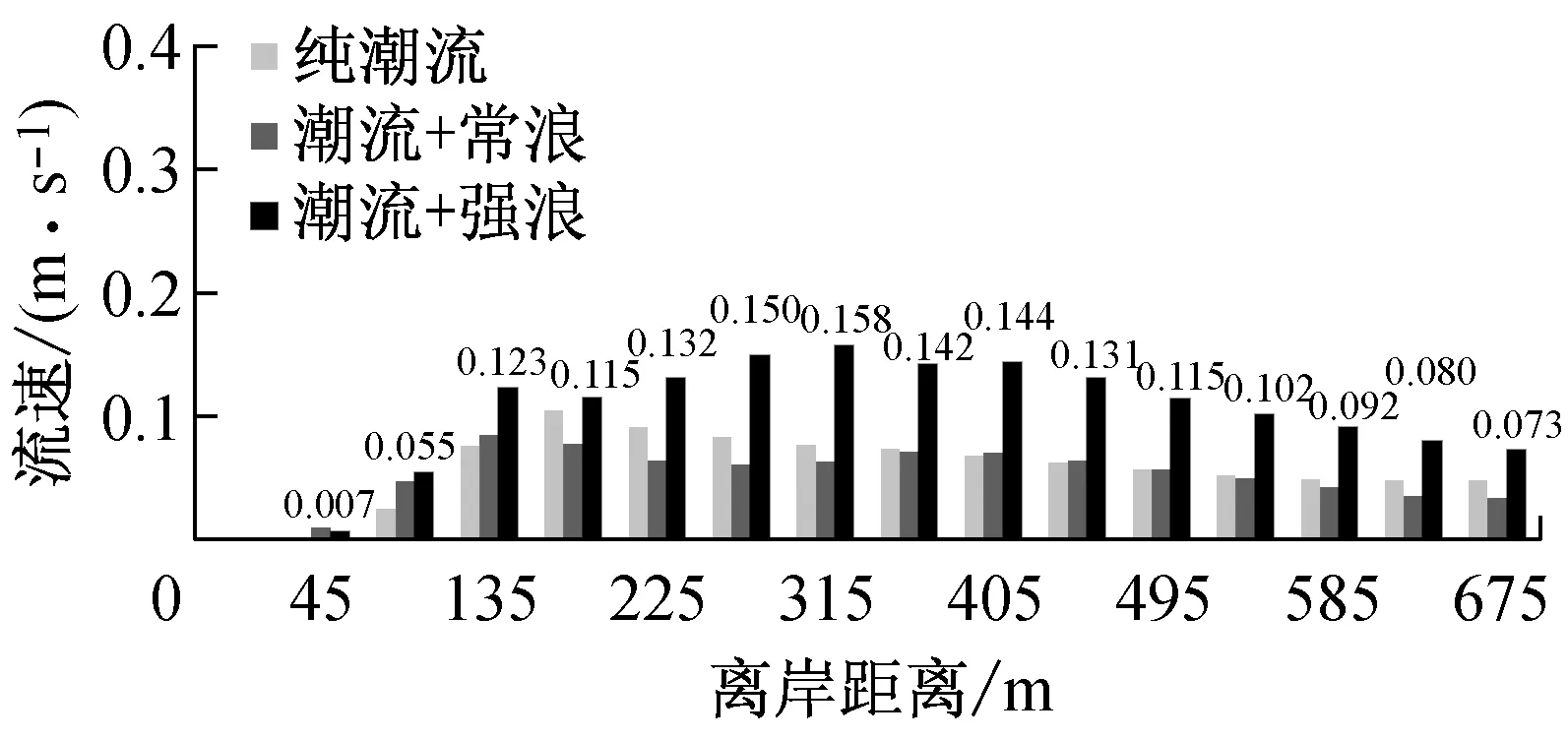
波浪传播到近岸浅水区域时，波陡迅速增大，波形扭曲前倾直至破碎，在破碎带内大量波浪能量消耗于摩擦和掀动泥沙，同时形成波生流.图10为涨落急时刻近岸各剖面流速分布.结果表明：随着水深、地形的变化，波浪对流速的影响幅度不同.P1剖面受北侧龟模屿影响，波流耦合作用时流速变化规律相对不明显.由P2和P3剖面涨落急时刻流速分布可知，离岸区域(离岸距离超过675 m)流速增加幅度较小；越接近波浪破碎带，波浪对潮流的作用逐渐增大，离岸约135～360 m范围内流速显著增大，最大涨幅可达200%.近岸区域(离岸距离小于45 m)，由于落急时刻潮滩干出，波浪不参与计算，涨急时刻浅水区波浪经过多次破碎，波能已大幅衰减，因此对流速影响不明显，这也与Baidei在一系列水槽试验中给出的随机入射波作用下的近岸剖面流速分布趋势相一致[21].

a 常浪P1

b 强浪P1

c 常浪P2

d 强浪P2

e 常浪P3

f 强浪P3

从三个剖面流速分布可知：波流耦合作用下，落急时刻流速增加幅度明显大于涨急时刻，且落急时刻各剖面最大流速也较涨急时刻略大，考虑是由于落急时刻，波高衰减较涨急时刻明显，落急波高明显小于涨急时刻及纯波浪作用(图9b)，即有更多波能向水流动能转化，形成前进水流.在常浪作用时，由于破碎波能较小，近岸水流流速增减不明显；强浪作用时，波生流大幅增加.龙凤头近岸海域海床坡度约在0.01左右，文献[22]中给出：对于底坡很缓(坡度小于1/100)的水域，在规则波条件下，破碎波高与破碎水深的比值不小于0.55，但在不规则波条件作用下，该数值应有所减小.表3为P2剖面涨落急时刻近岸波高、水深及其比值，结合考虑图10和表3，将龙凤头海滩近岸海域破碎波高与破碎水深的比值定为0.5，即涨急时刻，P2剖面离岸180 m以内(波高与水深比值接近或大于0.5)为波浪破碎带；落急时刻，离岸225 m以内(波高与水深比值接近或大于0.5)为波浪破碎带，在此水域内波浪发生多次破碎，形成沿岸流.综上可知，波浪辐射应力在破碎带附近对潮流的影响最大，叠加到潮流中可显著影响流速的大小，因此在对近岸浅水区进行流场模拟计算时，应考虑波浪对流的影响.

4　结论

福建海坛湾地理位置和水文气候特征决定了湾内波流相互作用的复杂性，本文利用MIKE 21软件建立了海坛湾波流双向耦合下水动力数学模型，先进行了模型了验证，再分别对波流双向耦合作用下的潮流场和波浪场进行了模拟，并与纯潮流和纯波浪作用下的潮流场和波浪场进行了比较分析，得到以下主要结论：

(1) 在潮流作用较强且波流异向明显的区域，波高增大显著.波高变化和流速变化呈现一定的负相关关系，波向和水流流向相顺时，波高减小，流速增大；相逆时，波高增大，流速减小.

(2) 波浪在浅水区域的衰减速率主要取决于底床坡度及沉积物特性，因此涨落急时刻波高在近岸区域的衰减速率和纯波浪作用下较一致.

a 涨急时刻P1

b 落急时刻P1

c 涨急时刻P2

d 落急时刻P2

e 涨急时刻P3

f 落急时刻P3

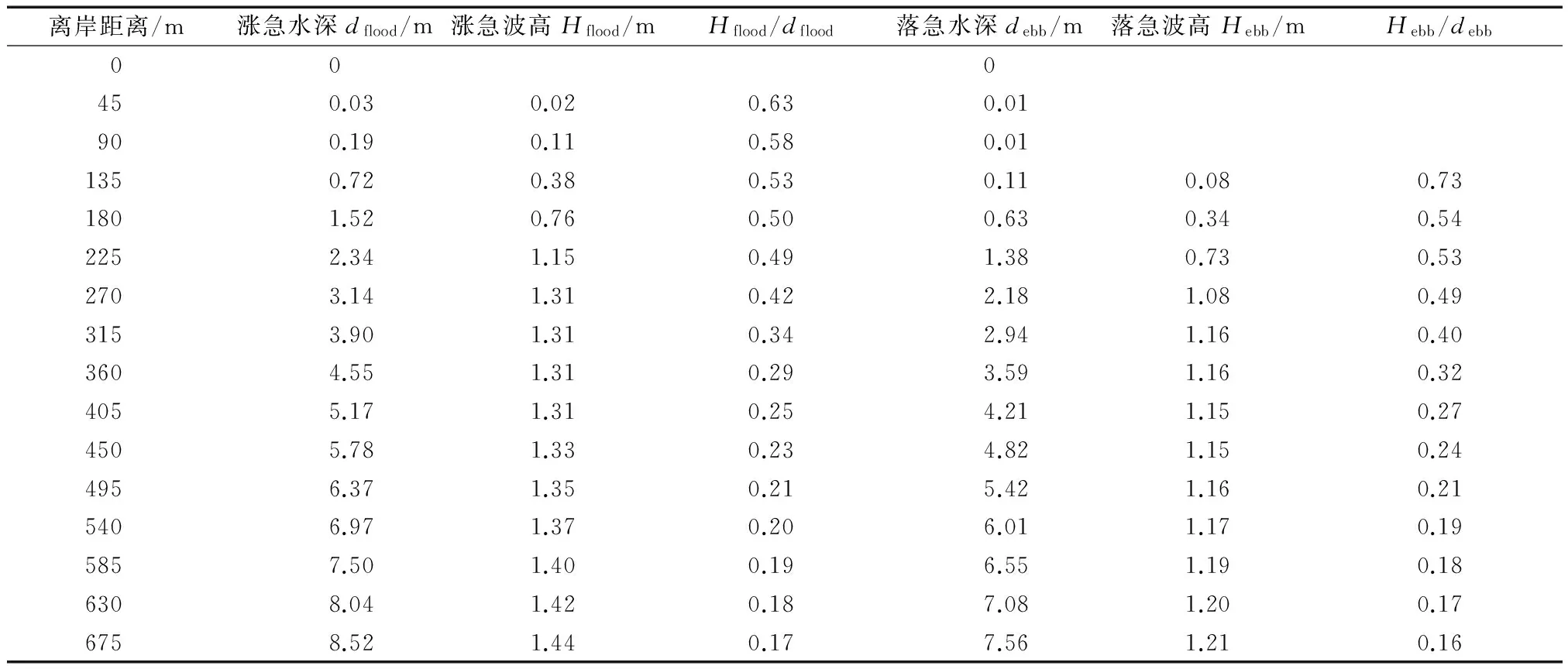
离岸距离/m涨急水深dflood/m涨急波高Hflood/mHflood/dflood落急水深debb/m落急波高Hebb/mHebb/debb000450.030.020.630.01900.190.110.580.011350.720.380.530.110.080.731801.520.760.500.630.340.542252.341.150.491.380.730.532703.141.310.422.181.080.493153.901.310.342.941.160.403604.551.310.293.591.160.324055.171.310.254.211.150.274505.781.330.234.821.150.244956.371.350.215.421.160.215406.971.370.206.011.170.195857.501.400.196.551.190.186308.041.420.187.081.200.176758.521.440.177.561.210.16

(3) 由于涨急时刻近岸水深明显大于落急时刻，因此落急时刻波高开始显著衰减的位置明显早于涨急时刻，且入射波高越大，波高衰减位置越早.

(4) 波浪辐射应力在破碎带附近对潮流的影响最大，叠加到潮流中可显著影响水体流速的大小.

[1]李玉成.波浪对海上建筑物的作用[J].大连：大连理工大学出版社，1990.

LI Yucheng. Wave action on maritime structures [M]. Dalian: Dalian University of Technology Press, 1990.

[2]Malarkey J, Davies A G. Modelling wave-current interactions in rough turbulent bottom boundary layers [J]. Ocean Engineering, 1998, 25(2): 119.

[3]Davies A G, Soulsby R L, King H L. A model of the vertical structure of the wave and current bottom boundary layer [J]. Modeling Marine Systems, 1990(2): 263.

[4]吴永胜, 练继建, 张庆河, 等. 波浪和水流共同作用下水流时均流速分布[J]. 水利学报, 2001, 32(1): 35.

WU Yongsheng, LIAN Jijian, ZHANG Qinghe,etal. Distribution of time average velocity in wave-current combined flow [J]. Journal of Hydraulic Engineering, 2001, 32(1): 35.

[5]孙昭晨, 王世澎. 波浪辐射应力对潮流的影响[J]. 大连理工大学学报, 2006, 46(5): 730.

SUN Zhaochen, WANG Shipeng. Effect of wave radiation stresses on tidal current [J]. Journal of Dalian University of Technology, 2006, 46(5): 730.

[6]国家海洋局第三海洋研究所.平潭龙凤头沙滩修复项目水文观测报告[R].福建:国家海洋局第三海洋研究所, 2012.

Third Institute of Oceanography, State Oceanic Administration. Report of hydrological observation on beach restoration project of Longfengtou, Pingtan [R]. Fujian: Third Institute of Oceanography, State Oceanic Administration, 2012.

[7]汤军健, 温生辉, 陈楚汉. 海坛海峡二维潮流场数值模拟[J]. 台湾海峡, 2006, 25(4): 533.

TANG Junjian, WEN Shenghui, CHEN Chuhan. Numerical simulation of two-dimensional tidal current model for Haitan Strait [J]. Journal of Oceanography in Taiwan Strait, 2006, 25(4): 533.

[8]杜凌, 左军成, 张建立, 等. 台湾海峡潮汐潮流的有限元模拟[J]. 海洋湖沼通报, 2005(4): 1.

DU Ling, ZUO Juncheng, ZHANG Jianli,etal. Simulation of tide and tidal current in the Taiwan Strait by finite element method [J]. Transactions of Oceanology and Limnology, 2005(4): 1.

[9]刘浩, 吴青松, 骆智斌, 等. 福清湾潮流场及污染物输运特性的模型研究[J]. 厦门大学学报:自然科学版, 2009, 48(1): 139.

LIU Hao, WU Qingsong, LUO Zhibin,etal. Model study on the tidal regime and poluutant transport in the Fuqing Bay [J]. Journal of Xiamen University: Natural Science, 2009, 48(1): 139.

[10]田永青, 潘爱军. 台湾海峡西部近海潮汐特征[J]. 台湾海峡, 2011, 30(4): 483.

TIAN Yongqing, PAN Aijun. Tidal chatacteristics in offshore sea of western Taiwan Strait [J]. Journal of Oceanography in Taiwan Strait, 2011, 30(4): 483.

[11]林航. 福建三沙湾的潮汐特征[J]. 福建水产, 2014, 36(4): 306.

LIN Hang. Tidal characteristics in the Sansha Bay of Fujian [J]. Journal of Fujian Fisheries, 2014, 36(4): 306.

[12]刘涛, 陈汉宝, 刘海源. 福建兴化湾波浪条件数值模拟研究[J]. 水运工程, 2007(3): 22.

LIU Tao, CHEN Hanbao, LIU Haiyuan. Numerical simulation research on wave condition of Xinghuawan Bay, Fujian [J]. Port & Waterway Engineering, 2007(3): 22.

[13]叶雨颖, 潘伟然, 张国荣, 等. 福建东山湾海浪现场观测的统计特征[J]. 厦门大学学报:自然科学报, 2007, 46(3): 386.

YE Yuying, PAN Weiran, ZHANG Guorong,etal. The field observations and statistical characteristics of wave in Dongshan Bay [J]. Journal of Xiamen University: Natural Science, 2007, 46(3): 386.

[14]张军, 许金电, 郭小钢. 福建沿海海域波浪能资源分析与评价[J]. 台湾海峡, 2012, 31(1): 130.

ZHANG Jun, XU Jindian, GUO Xiaogang. An evaluation and analysis of the ocean wave energy resource in nearshore waters of Fujian [J]. Journal of Oceanography in Taiwan Strait, 2012, 31(1): 130.

[15]栾曙光, 刘永孝, 赵凯. 闽中近岸西北行路径台风浪波向特征[J]. 海洋预报, 2012, 29(5): 65.

LUAN Shuguang, LIU Yongxiao, ZHAO Kai. Characteristics of wave direction caused by the northwest typhoon in the offshore of Fujian province [J]. Marine Forecasts, 2012, 29(5): 65.

[16]DHI Hydraulics. MIKE 21 & MIKE 3 flow model hydrodynamic and transport module science documentation [M]. Denmark: DHI Water & Environment, 2009.

[17]DHI Water & Environment & Health. MIKE 21 spectral wave module scientific documentation[M]. Denmark: DHI, 2009.

[18]孔令双, 戚定满, 万远扬, 等. 长江口海域波浪场模拟研究[J]. 水运工程, 2010(2): 46.

KONG Lingshuang, QI Dingman, WAN Yuanyang,etal. Numerical simulation of wave field in the Yangtze Estuary [J]. Port & Waterway Engineering, 2010(2): 46.

[19]WANG Binyu, KUANG Cuiping, SHAN Yunchi,etal. Hydrodynamic response to a groin system at Longfengtou Beach, China [C]∥ Proceedings of the 24th International Ocean and Polar Engineering Conference. Busan: International Society of Offshore and Polar Engineers, 2014: 1070-1075.

[20]Willmott C J. On the validation of models [J]. Physical Geography, 1981, 2(2): 184.

[21]Badiei P, Kamphuis J W, Hamilton D G. Physical experiments on the effects of groins on shore morphology [C]∥ Proceedings of the 24th International Conference on Coastal Engineering. Kobe: American Society of Civil Engineers, 1994: 1782-1796.

[22]邱大洪. 工程水文学[M]. 北京:人民交通出版社, 2008.

QIU Dahong. Engineering hydrology [M]. Beijing: China Communications Press, 2008.

Study of Hydrodynamics Using a Bi-Directional Wave-Current Coupled Model in Haitan Bay, Fujian Province

KUANG Cuiping1, WANG Binyu2, GU Jie3, LEI Gang4

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. Guangxi Vocational and Technical College of Communications, Nanning 530216, China; 3. College of Marine Sciences, Shanghai Ocean University, Shanghai 201306, China; 4. Third Institute of Oceanography, State Oceanic Administration, Xiamen 361005, China)

In this paper, a 2D bi-directional wave-current coupled model in Haitan Bay was set up based on the MIKE 21 SW wave module and FM current module. The effects of wave and current interactions were incorporated by extracting the radiation stresses from wave simulations into FM model, and extracting the water levels and velocities from flow simulations into SW model, respectively. The flow fields and wave fields in Haitan Bay under pure current and pure wave condition were simulated respectively, and calibrated by the field measured tidal flow and wave data. Then, the well validated models were employed to model the flow fields and wave fields under wave-current interaction. The results show that the wave-current interaction has a great influence on both flow velocity and wave height and the wave height significantly increases if the wave and current are in the opposite direction; the decay rate of wave height in the inshore area in both flood current and ebb current is in accordance with that in pure wave condition; the position for the wave height that begins to decrease in ebb current is obviously earlier than that in flood current; the radiation stress has a significant influence on the flow velocity in the wave breaking zone.

Haitan Bay; wave; current; wave-current coupled; MIKE 21

2015-10-08

匡翠萍(1966—), 女, 教授, 工学博士, 主要研究方向为海岸工程. E-mail: cpkuang@tongji.edu.cn

顾杰(1961—), 男, 教授, 工学博士, 主要研究方向为海洋环境. E-mail：jgu@shou.edu.cn

TV148+.5

A