地下结构抗震设计方法整体强制反应位移法

陈之毅， 谈忠傲， 楼梦麟

(1． 同济大学 土木工程防灾国家重点实验室， 上海 200092； 2. 同济大学 土木工程学院， 上海 200092)



地下结构抗震设计方法整体强制反应位移法

陈之毅1,2， 谈忠傲2， 楼梦麟1

(1． 同济大学 土木工程防灾国家重点实验室， 上海 200092； 2. 同济大学 土木工程学院， 上海 200092)

基于地震作用下地下结构主要受周围土层变形控制这一基本思想，在地下结构抗震设计方法强制反应位移法的基础上，探讨了一种新的抗震设计方法——整体强制反应位移法.新方法将土层变形施加到计算模型的整个土层有限元上以模拟地震作用，避免了原方法所施加土层变形传递到远离模型边界位置会发生衰减的现象.结合上海市某地铁车站的计算实例，详细介绍了该方法的具体实施步骤、基本特点.同时以动力时程法为基准，分析了该方法在不同地震动强度下的计算效果.研究表明,整体强制反应位移法的计算结果与动力时程法符合较好，设计理念体现了地下结构的震害机制，是一种方便有效的抗震设计方法.

地下结构； 震害特征； 整体强制反应位移法； 抗震分析与设计

近年来，地下工程大力发展，成为城市正常运转不可或缺的生命线工程.长期以来，人们普遍认为地下结构抗震性能优于地面结构，并没有充分重视地下结构的抗震设计，致使地下结构抗震研究发展相对迟缓.直至1995年日本阪神大地震，各种地下结构均遭受到严重的破坏，地下结构抗震才引起学者们的广泛关注.2008年“汶川”特大地震，地下工程同样遭受严重损害[1]，更加使人们意识到地下结构抗震设计的重要性.

相对于地上结构，地下结构由于受周围土层约束，其动力特性与地上结构相比具有一些明显不同的特点.地下结构的抗震设计与地面结构的抗震设计亦存在显著的差异.美国和日本等国家对地下结构的研究起步较早，提出了一些经典的抗震设计理论及相应的实用抗震设计方法[2].动力时程分析法作为一种适应性极强的方法，被广泛应用于地下结构在整个时程范围内地震响应的评估中.但它在复杂的边界条件处理、地震波筛选、土体非线性动力特性描述等方面存在诸多问题，且参数复杂，调试困难.反应位移法是一种经典的拟静力抗震设计方法，但其中地基弹簧系数对计算结果存在着决定性的影响，难以准确确定.若采用更为精确的静力有限元方法计算弹簧系数则又费时费力[3].近年来众多学者纷纷提出一些新的抗震设计方法，为动力时程法和反应位移法提供了重要补充[4].刘晶波等人提出地下结构Pushover法概念清晰，并且可对地下结构进行静力弹塑性分析[5-6]，但在实际应用中发现倒三角形的惯性加速度简化荷载形式不一定适用所有土层情况，且在推覆过程中若土层较软还可能先于结构破坏导致计算中断.更为关键的是，地下结构在地震作用下的响应受土层变形控制是人们对地下结构震害机制的普遍共识[7].但是目前所流行的地下结构抗震设计方法多是施加力或者惯性加速度对结构受力进行分析的，与基本认识不一致.

本文在地下结构抗震设计方法中的强制反应位移法的基础上，对等效地震荷载的加载方式进行了改进，提出整体强制反应位移法.并采用大型通用有限元软件ABAQUS对上海某地铁车站进行了数值模拟，以动力时程法为基准，详细分析了整体强制反应位移法计算结果，验证了新方法在地下结构抗震设计方面的有效性.

1　整体强制反应位移法

1.1整体强制反应位移法的提出

通过国内外学者的大量原型观测和模型试验，地下结构在地震作用下的反应一般被认为具有以下两个特点：① 地下结构本身并不存在主要振型，而是取决于周围的岩土环境；② 地下结构的变形主要受周围土层变形的控制[7].与地上结构抗震设计准则相仿，地下结构的抗震设计方法也应该建立在对其地震响应特征及震害机理科学认识的基础上.美国在上世纪60年代修建圣弗兰西斯科海湾地区的快速运输系统(简称BART)运用的BART法就是其有力佐证.BART法正确认识到地下结构的震害机理是地震引起的土层变形作用于地下结构产生相应内力，于是以该基本特征为设计准则开展抗震设计.该方法设计的地铁系统成功经历了1989年旧金山里氏7级Loms Prieta地震的考验，足以说明基于结构震害机理进行抗震设计的合理性[8].现行很多地下结构抗震设计方法也是基于以上两点认识提出的.根据这些方法对土层的处理又可以大致把它们分成两类：① 用地基弹簧代替土层作用，属于荷载结构法，代表的设计方法有反应位移法；② 用有限元等数值方法模拟土层，充分考虑土体-结构的相互作用，属于地层结构法，代表方法有Hamada[9]等人提出的强制反应位移法(FEM (finite element method) seismic deformation method, FSDM).

反应位移法将地震作用下的土层变形通过地基弹簧以静荷载的形式施加在结构上[2].其优势在于模型相对简单，概念清晰，且具有较为严密的理论基础，但是离散的地基弹簧无法真实体现实际工程中土层自身之间的相互作用[3]. 因而刘晶波等人提出了整体式反应位移法，将土层变形施加在除去结构的土层有限元模型上，得到相应的节点反力，施加在结构上.该方法考虑了土层之间的相互作用，避免了传统反应位移法中地基弹簧系数带来的误差.强制反应位移法基本概念同样简单明了.如图1a[7]所示，强制反应位移法将自由场的地震反应位移施加在模型边界上，然后计算模型内部土层变形及结构内力.Akira[7]研究表明：强制反应位移法的计算结果误差较大.因为该荷载处理方式造成的结果就是自由场应变只是被准确传递到拟静力模型的边界位置及其附近的土体范围内，而远离边界位置尤其是结构周围的土体，由于土体阻尼的影响，应变已经明显衰减20%～50%[7].对此，Hamada等人提出了修正强制反应位移法.该方法的示意图如图1b所示，主要是根据自由场一维地震反应计算得到地层应变，换算成等效节点荷载并施加到整体土体-结构模型上.该方法同时考虑了模型边界处的土层剪力，因此提高了强制反应位移法的计算精度.但是，该方法采用施加力而非施加位移(变形)的加载方式，其本质与Katayama[10]等人提出的反应加速度法(ground response acceleration method, GRAM)是一致的.反应加速度法的示意图见图1c.

基于前人的研究不难发现，现行大多数抗震设计方法依然是采用力这种荷载形式计算地下结构在地震作用下的内力的.这可能是受到早先发展的地上结构抗震设计观念的影响，因为地上结构的地震响应受惯性力控制，抗震设计方法采用施加惯性力的方式更加合理.然而在地下结构遭受地震作用时，惯性力所引起的内力并不大，地层变形及土体剪应力占据主要部分[11-12].为此本文在强制反应位移法的基础上进行改进，提出整体强制反应位移法，延续了其基于地下结构震害特征进行抗震设计的思想，将地震作用下的地层位移施加到整个土层有限元模型上，而不是模型边界上.该方法的模型建立、边界条件等与现行的反应加速度法相似，不同点在于荷载形式.反应加速度法将土层地震反应分析得到的最不利水平惯性加速度施加到相应埋深的土层和结构上，通过产生的水平惯性力来模拟地震作用.整体强制反应位移法则将土层地震反应分析得到的最不利水平位移强制施加到拟静力模型的土层上，使土体和结构产生相应变形，从而计算结构在地震作用下的内力，整个过程中忽略结构自身在地震中产生的惯性力的影响.

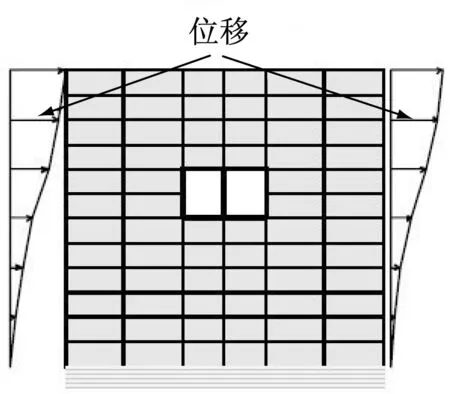
a 强制反应位移法

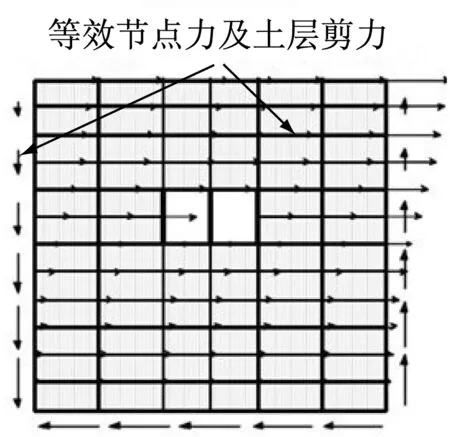
b 修正强制反应位移法

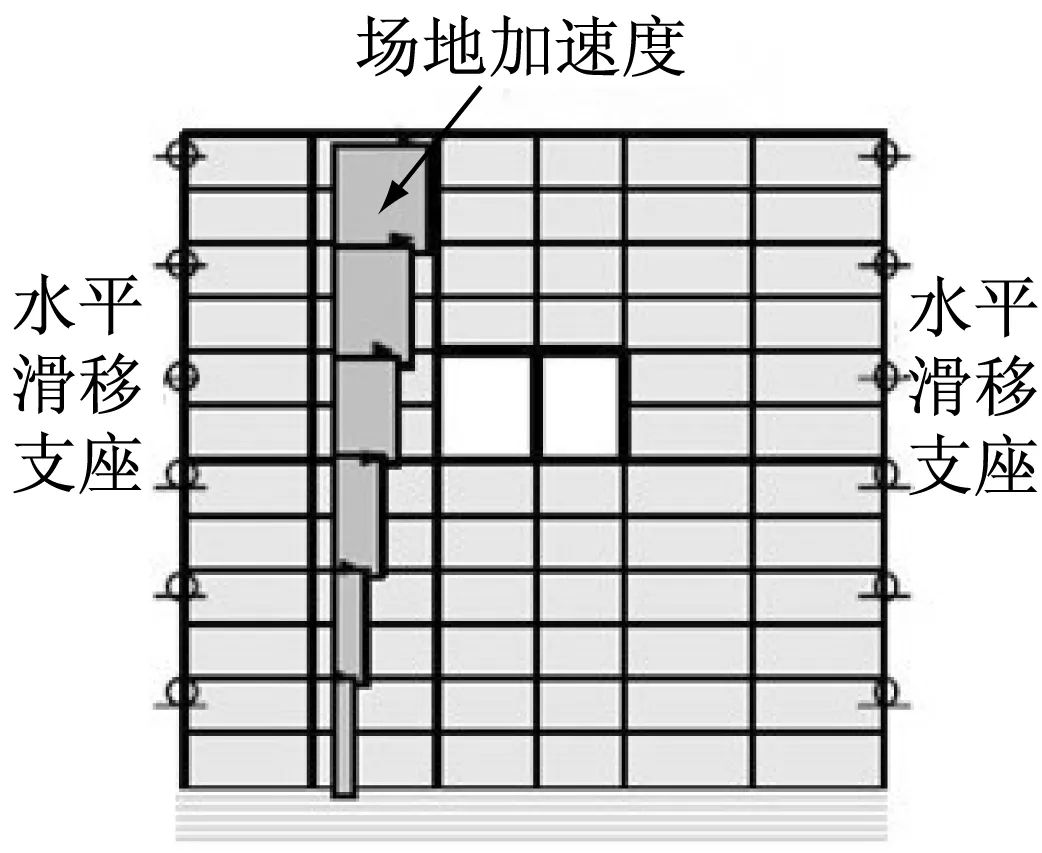
c 反应加速度法

1.2整体强制反应位移法的实施步骤

(1) 求解等效地震荷载.最不利土层水平位移可以采用等效线性化程序SHAKE91[13]，EERA或者通用有限元分析软件对自由场进行一维土层地震反应分析，读取自由场地下结构顶底板位置达到最大水平相对位移时刻，土层水平位移沿深度的分布. 实际计算中，选取N条适用于该场地的地震波，分别求得每条地震波计算所得最不利瞬时位移分布，取其平均值作为计算的等效地震荷载.

(2) 建立拟静力模型并进行地应力平衡.利用有限元软件建立土体-结构相互作用拟静力模型.为计算模型在自重作用下的反应，模型底面边界固定，侧向边界水平向约束，竖向自由.对模型施加重力，并进行地应力平衡.

(3) 重新定义边界条件.为了施加强制位移，模型侧向边界水平向需取消约束.故撤销水平向约束代之以地应力平衡之后的水平支座反力，同时约束侧向边界各节点的竖向位移，底面边界仍保持固定.

(4) 进行拟静力计算.将第一步计算所得的最不利土层水平位移施加到拟静力模型的土层上，计算结构在地震作用下的响应.

2　方法验证

2.1模型建立

该地铁车站为地下4层3跨岛式站台车站结构.围护结构均采用1.2 m地下连续墙.地下4层内衬厚度为0.8 m，地下2,3层内衬厚度为0.6 m，地下1层内衬厚度为0.4 m.取如图2所示的标准断面.车站总宽度为23.6 m，总高度为27.21 m，站台中心处埋深30.92 m.上2层中柱尺寸为0.7 m×1.1 m，下2层中柱尺寸为0.7 m×1.4 m，中柱间距为8 m.混凝土材料密度为2.5 g·cm-3，泊松比为0.2，中柱采用C45混凝土，弹性模量为33.5 GPa，其余部位采用C35混凝土，弹性模量为32.5 GPa；钢筋材料密度为7.8 g·cm-3，泊松比为0.3，弹性模量为200 GPa.

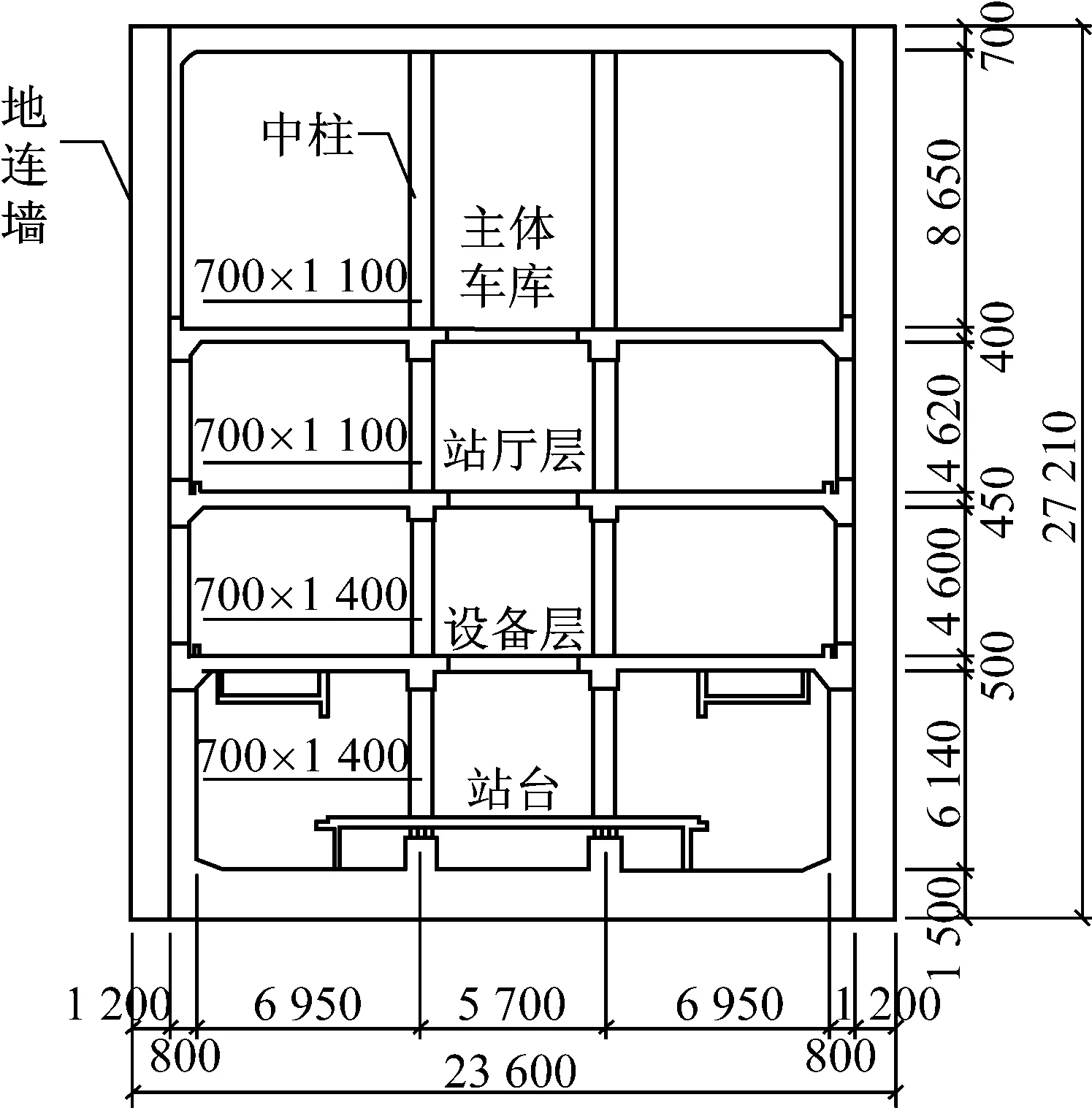
图2　车站标准断面 (单位：mm)

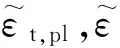
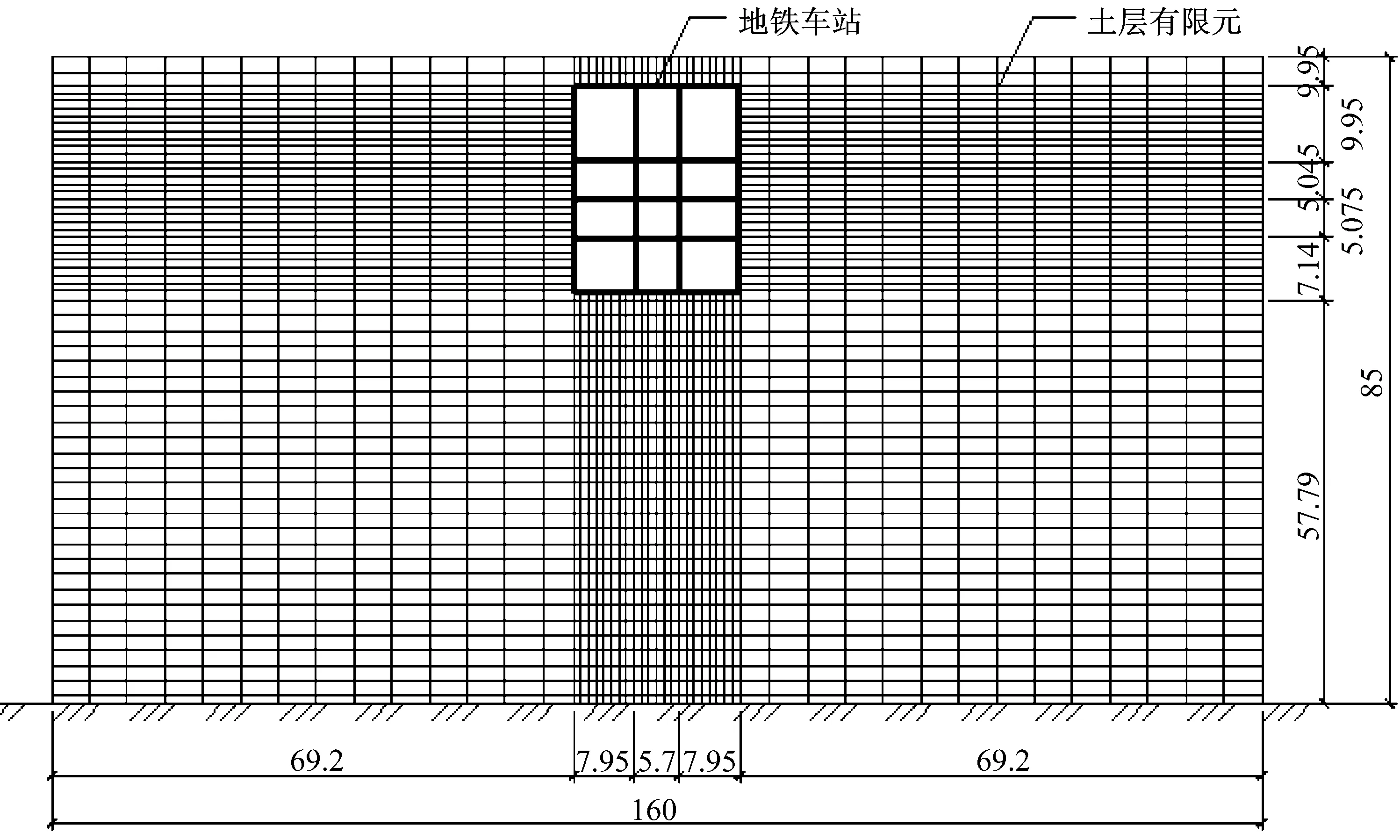
图3　二维拟静力模型(单位：m)

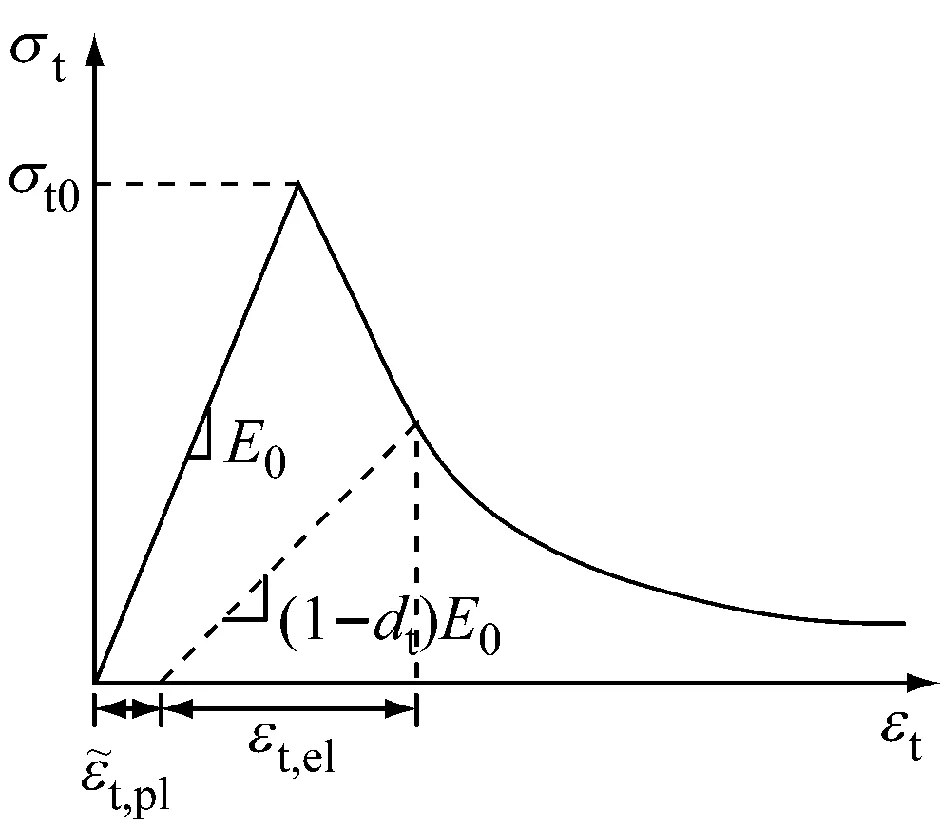
a 拉伸

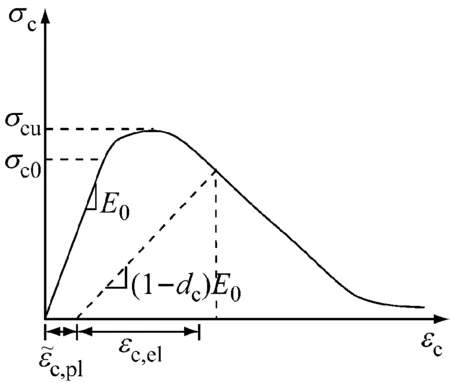
b 压缩

同时，作为计算校核的基准，建立了如图5所示的二维动力时程模型.模型长500 m，高85 m，结构尺寸、材料参数以及土层参数等设定与拟静力模型相同.底面边界固定竖向位移，为了更好地减弱侧向边界对地震波反射的影响，侧向边界使用无限元(CINPE4)模拟远场. 分析步采用ABAQUS隐式动力分析步，时间增量步长的控制采用自动步长技术.

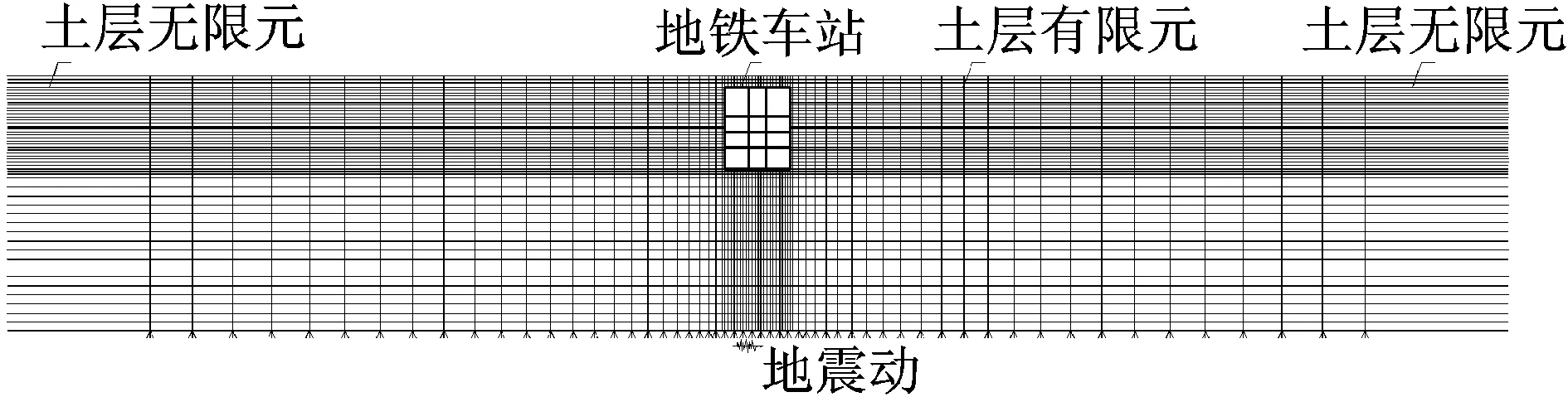
图5　二维土体-结构动力时程模型(单位：m)

2.2输入地震动

动力时程分析时地震动沿水平向输入模型底部.计算采用2条天然波及1条人工波，分别为El-centro波、Imperial Valley波和上海人工波，时程曲线见图6.为了研究该方法在不同地震动强度下的计算效果，将地震动地面峰值加速度(peak ground acceleration, PGA)调整到0.1g，0.2g，0.4g，作为3种计算工况.

2.3等代地震荷载的计算

根据《上海市地下铁道建筑结构抗震设计规范》

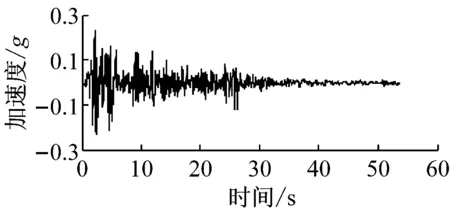
a El-centro波

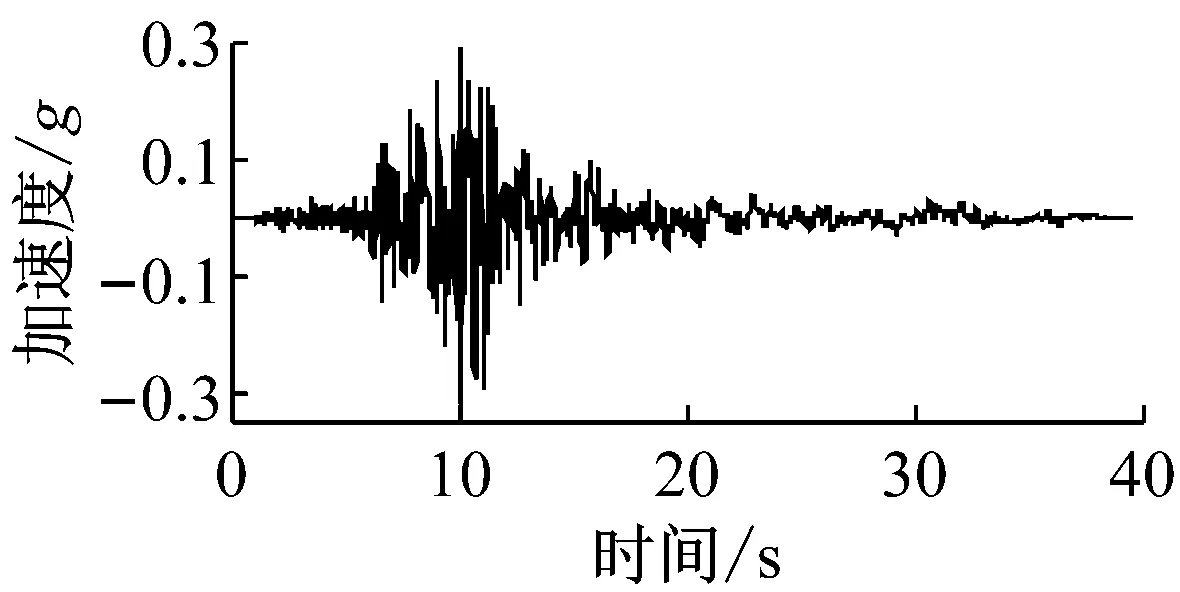
b Imperial Valley波

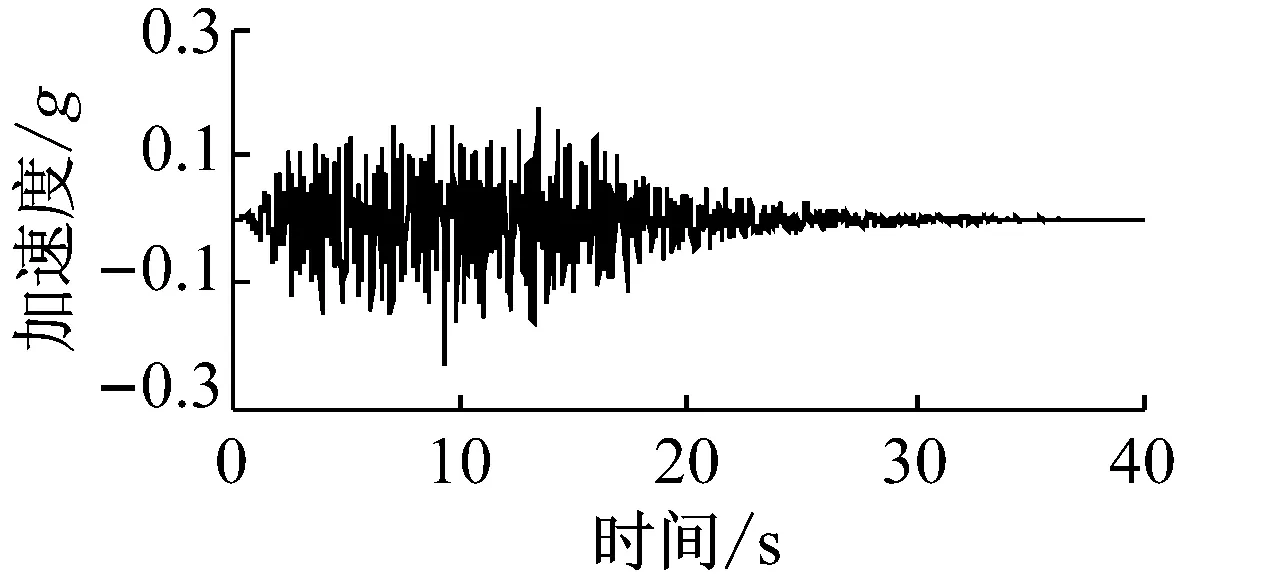
c 上海人工波

中D.2.1条，本文采用动力有限元进行土层地震反应分析.通过ABAQUS建立二维自由场动力时程模型，自由场模型与土体-结构动力时程模型采用相同的土体本构及参数，用无限元模拟远场，地震波施加在有限元底部.各工况土层最不利水平相对位移分布如图7所示.

各个工况下3条地震波各自计算所得最不利瞬时水平位移分布取平均之后所得到的等代地震荷载的分布曲线规律基本相同.地面与基岩的最大相对位移分别为7.1，13.0，21.4 cm.结构顶底板位置的土层最大相对位移分别为6.0，10.9，15.8 cm.

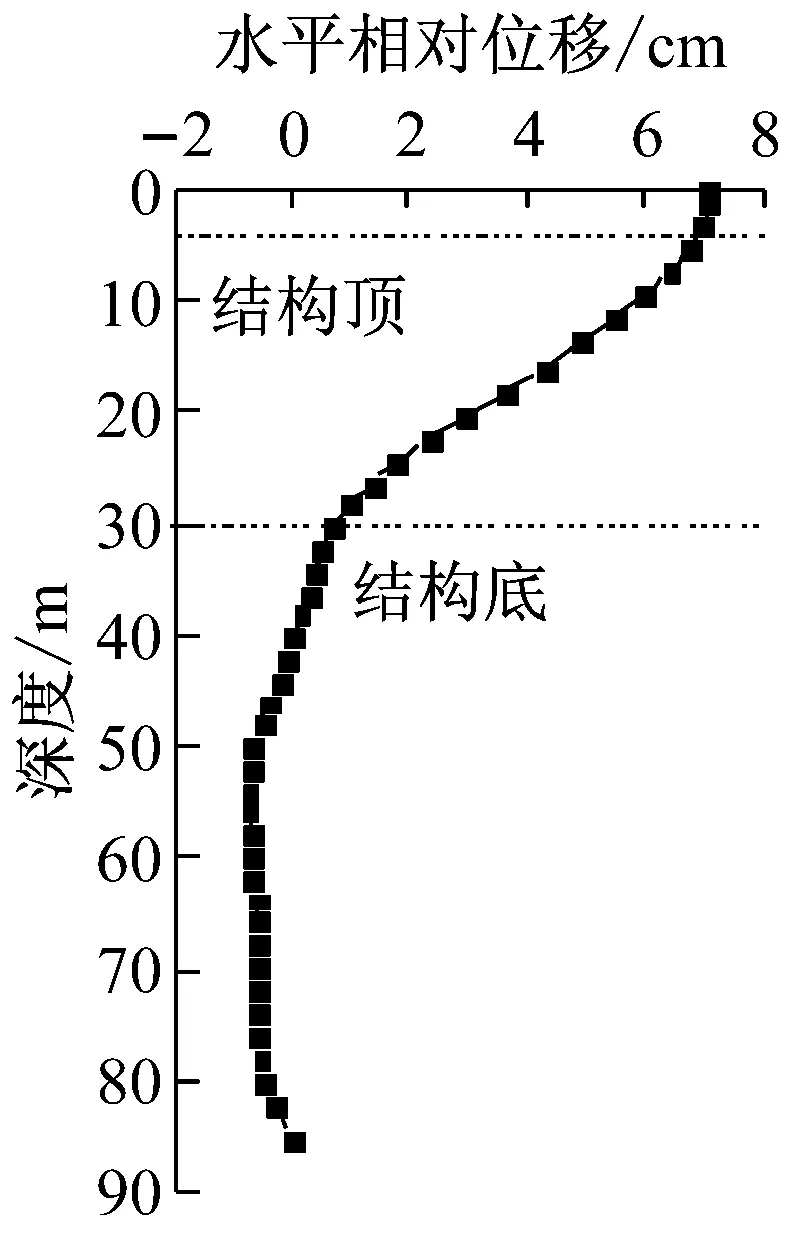
a PGA=0.1 g

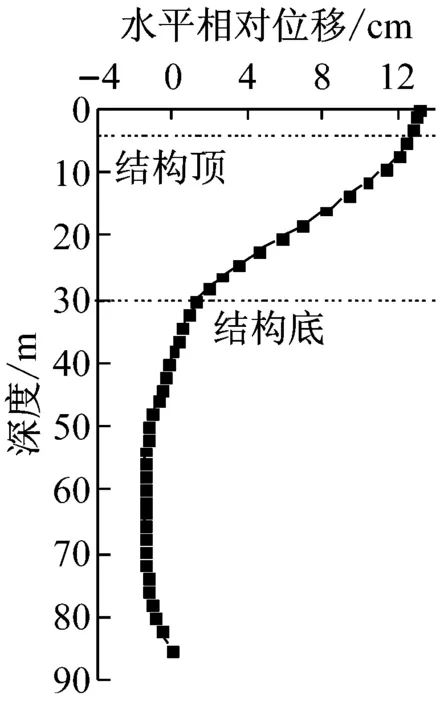
b PGA=0.2 g

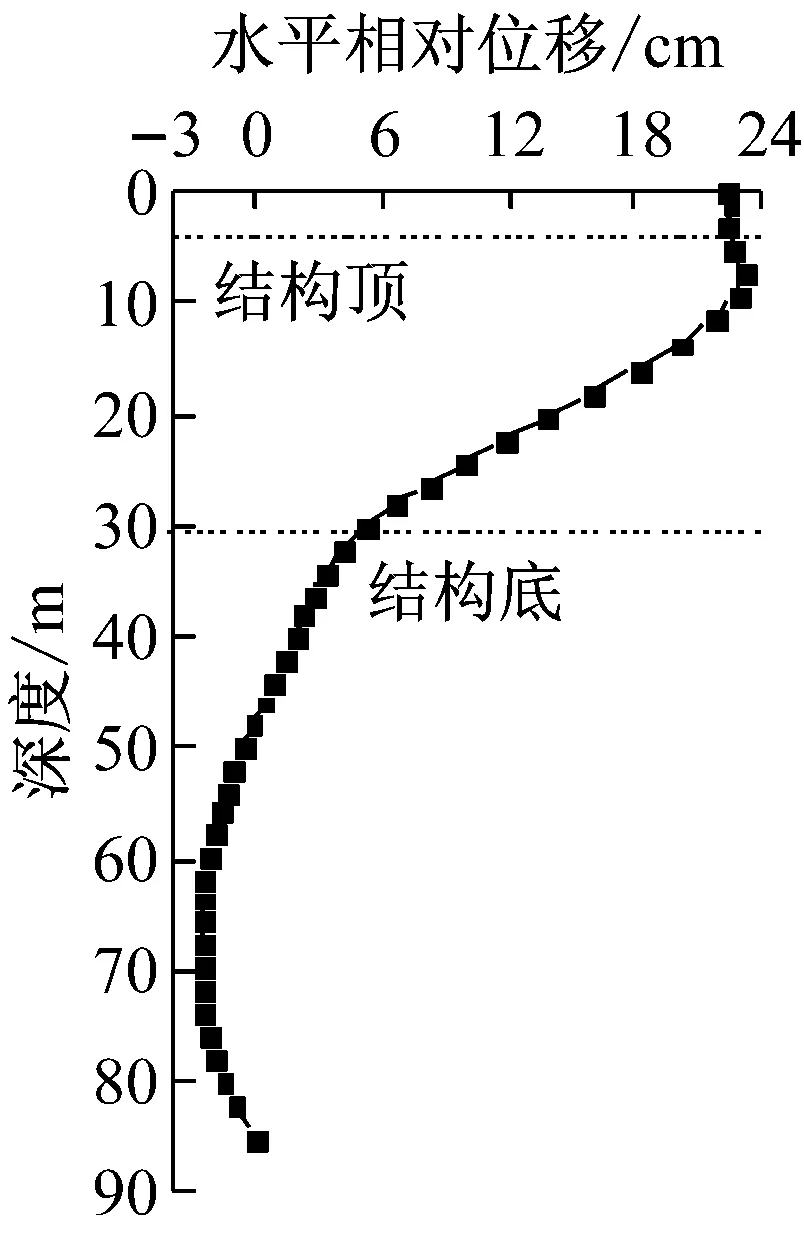
c PGA=0.4 g

2.4计算结果分析

2.4.1最不利状态的确定及控制截面的选取

为了合理分析整体强制反应位移法的计算精度，需采用动力时程法对其结果进行校核.将选取的3条地震波分别输入到土体-结构动力时程模型中计算结构的动力响应. 把动力分析所得结构顶底板达到最大相对位移的时刻作为结构最不利状态，分别读取同一PGA下不同地震波各自最不利状态的计算结果，并求其平均值作为动力分析的最终结果. 另一方面，将自由场地震反应分析计算得出的等效地震荷载输入到拟静力模型中计算结构内力,并将整体强制反应位移法计算的结构顶底板达到最大相对位移时的结果与动力时程分析的结果作对比.

对比分析整体强制反应位移法与动力时程法结构最不利状态下的塑性分布情况可以发现，侧墙底端、中柱顶底端及部分与中柱相连的楼板节点处是该结构相对薄弱的位置. 因此，选取如图8所示的控制截面A～F进行计算结果的对比.

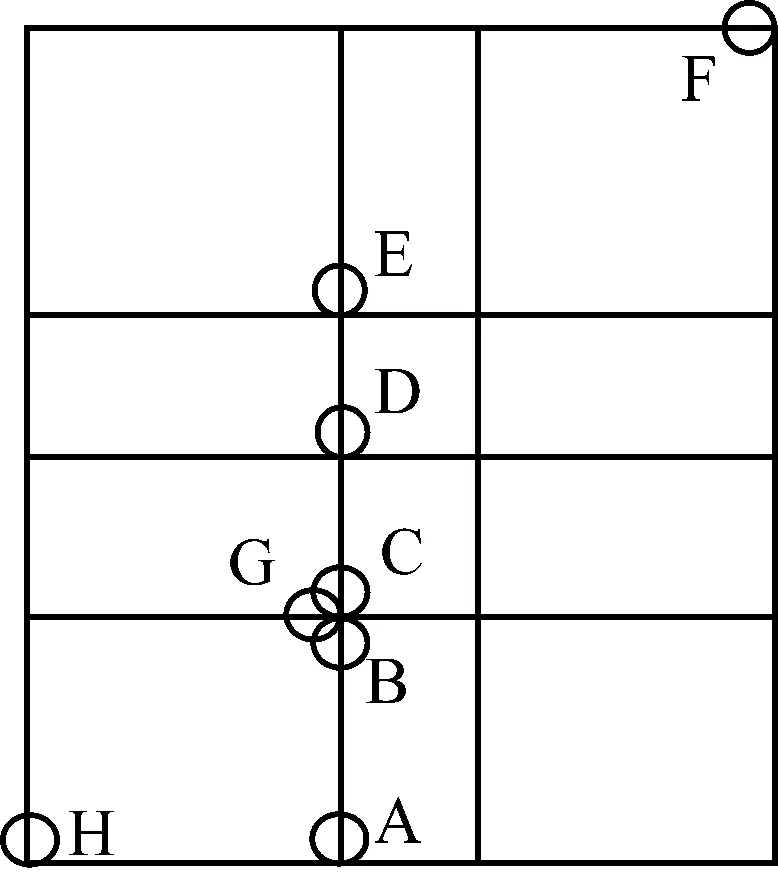
图8　控制截面位置标示

2.4.2内力结果分析

表1、表2分别给出了结构控制截面的弯矩计算结果与剪力计算结果.其中边墙及板的内力均为每米结构的总内力，中柱则为单根中柱的内力.图9是整体强制反应位移法及动力时程法计算结果的对比情况.图中,Md,Qd分别为动力分析法计算得到的弯矩和剪力;Ms,Qs分别为整体强制反应位移法计算得到的弯矩和剪力. 由图表可以看出，在各个地震动强度下，大部分控制截面上施加土层位移的整体强制反应位移法的计算结果比较接近动力时程分析得出的内力结果.在地震动强度为0.1g情况下，整体强制反应位移法总体误差在10%左右，控制截面D，E弯矩误差仅为1%，剪力误差也只有4%；最大误差出现在控制截面C，计算所得的弯矩和剪力误差较大，分别为39%和22%.在地震动强度为0.2g情况下，就弯矩而言，整体强制反应位移法计算误差在15%左右，最小误差仅为0.6%，个别控制截面误差较大达37%；剪力的计算误差基本在5%～15%，控制截面C误差稍大为27%.在地震动强度为0.4g情况下，整体强制反应位移法依然有较好的计算效果，大部分控制截面误差低于10%.

从以上分析可以看出，本文提出的整体强制反应位移方法与动力时程法计算结果在大部分截面上符合良好.表明整体强制反应位移法能够较好地预测地下结构在地震作用下的内力响应.

2.4.3变形结果分析

表3、表4给出了不同工况下车站侧墙及左侧中柱的变形计算结果.数据为两种计算方法在对比状态下，侧墙或中柱与楼板各相连节点相对于底板节点的水平位移.由底层到顶层4个节点编号分别为L1,L2,L3,L4.图10反映了各工况下两种计算方法计算所得侧墙及中柱由下至上4个节点的变形结果对比情况.图中，dd表示动力分析方法计算所得变形，ds表示整体强制反应位移法计算所得变形. 根据动力时程的分析结果，在PGA为0.1g时，结构中已有少部分截面产生等效塑性应变，表明该处截面部分发生屈服进入塑性.结构最大层间位移角约为1/574，小于规范[14]规定的弹性层间位移角极限值1/550，说明结构基本处于弹性状态；在PGA为0.2g及0.4g时，等效塑性应变大于零的截面进一步增多，中柱顶底端及部分楼板端部基本进入塑性，最大层间位移角分别达到1/289和1/167，已经超越弹性极限，结构进入弹塑性状态.

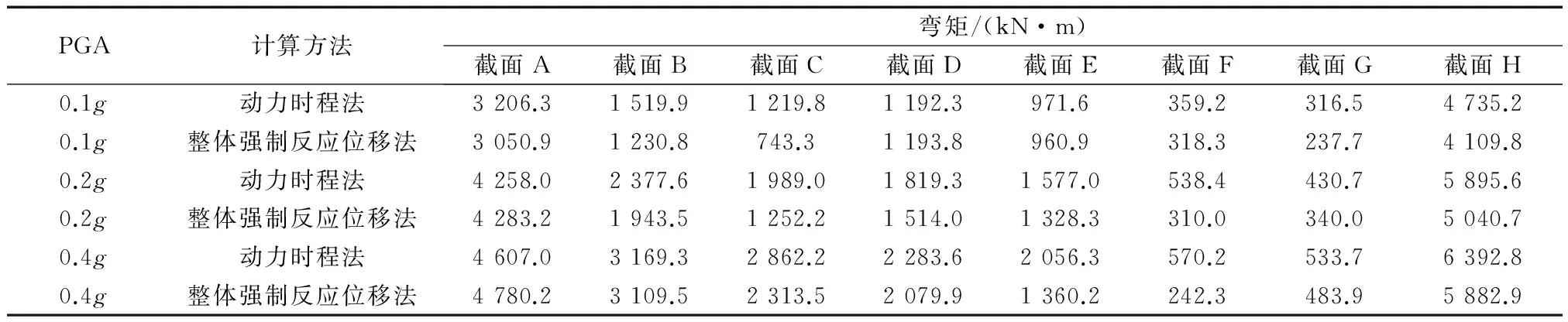
表1　不同工况下的弯矩计算结果

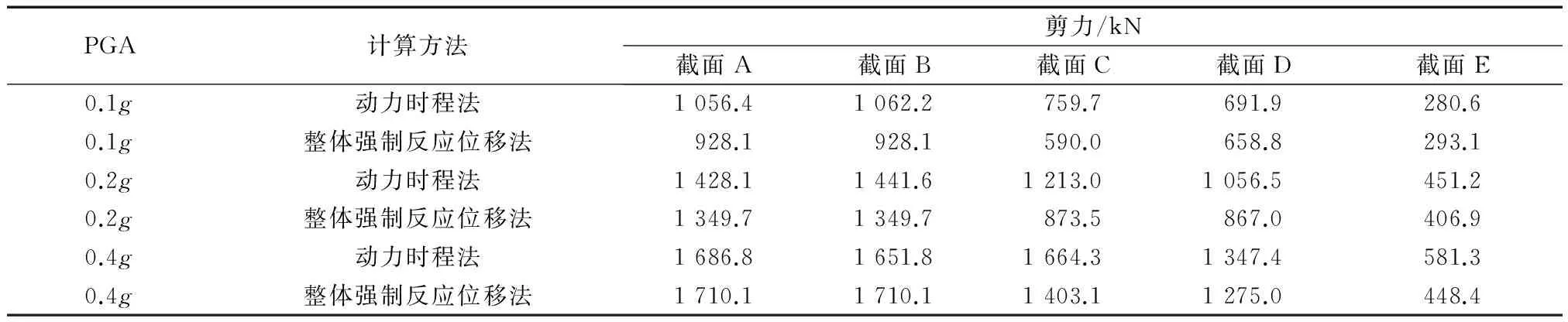
表2　不同工况下的剪力计算结果

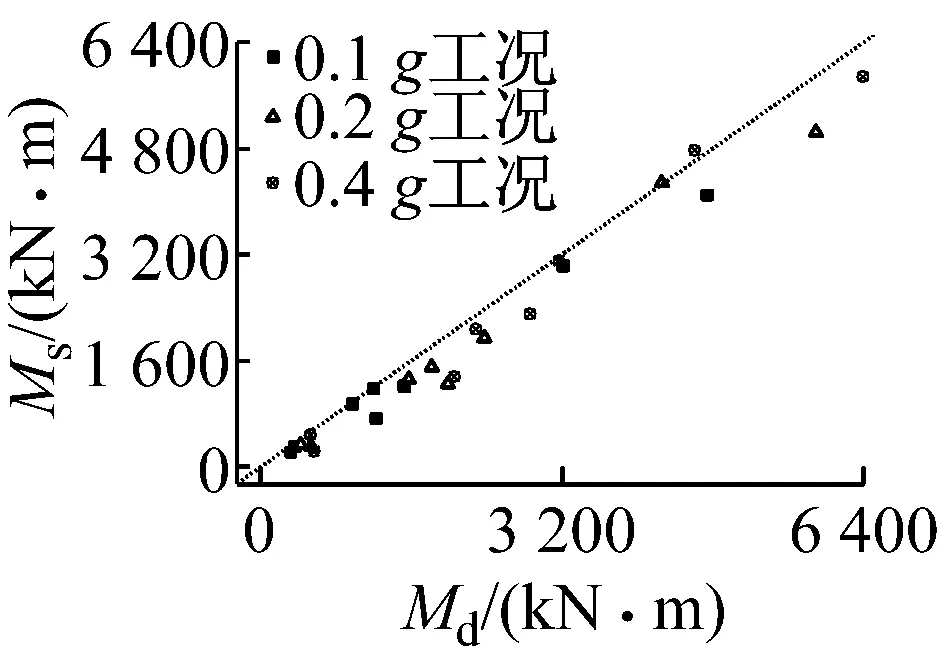
a 弯矩对比

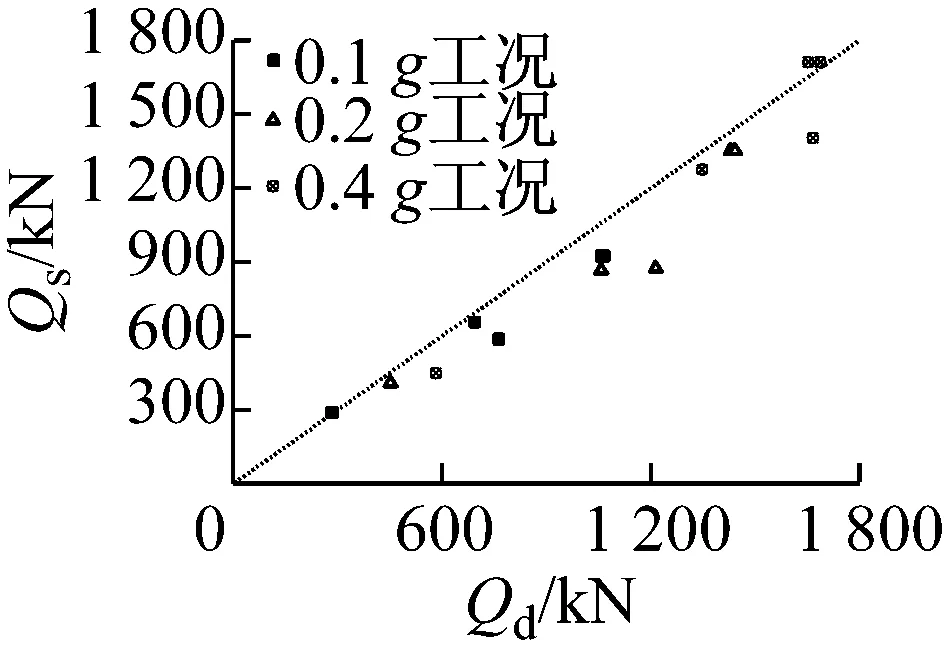
b 剪力对比

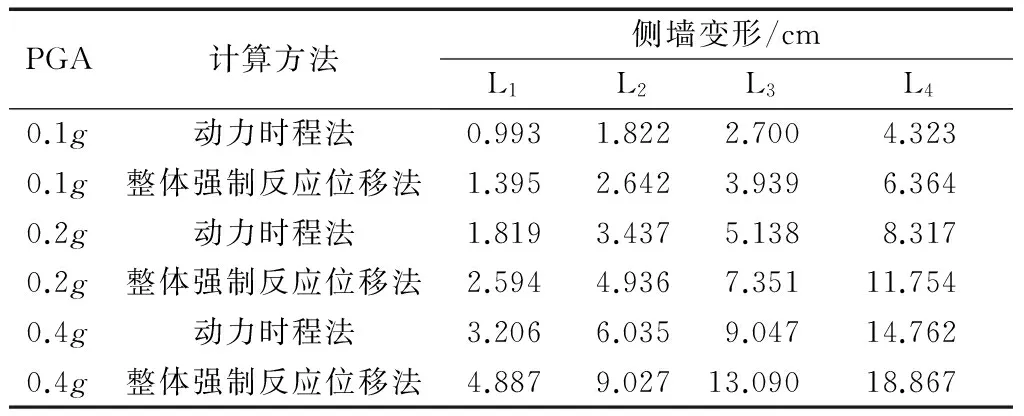
PGA计算方法侧墙变形/cmL1L2L3L40.1g动力时程法0.9931.8222.7004.3230.1g整体强制反应位移法1.3952.6423.9396.3640.2g动力时程法1.8193.4375.1388.3170.2g整体强制反应位移法2.5944.9367.35111.7540.4g动力时程法3.2066.0359.04714.7620.4g整体强制反应位移法4.8879.02713.09018.867

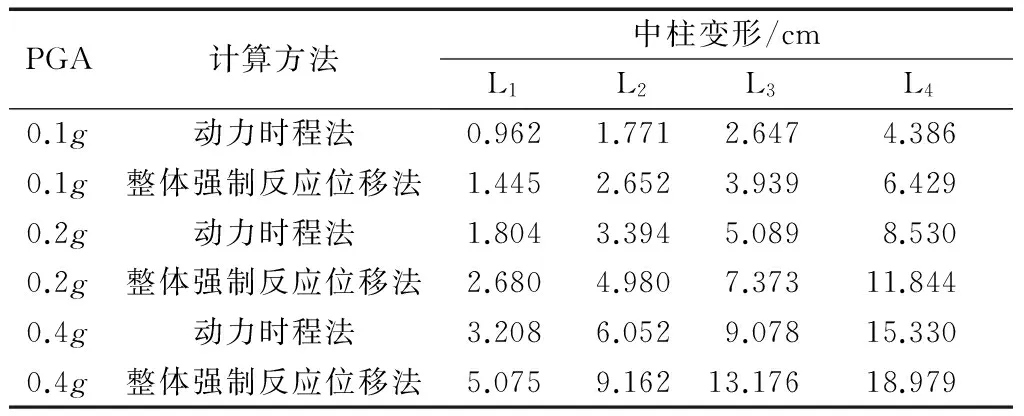
表4　不同工况下的中柱变形结果

a侧墙变形对比b中柱变形对比

图10各工况变形结果对比

Fig.10Comparison of deformations under different conditions

从整体上可以看出，整体强制反应位移法的计算结果偏大于动力时程的分析结果.其原因主要在于建模时考虑了地连墙的抗震作用，故车站结构的整体刚度较大.结构的存在使周边土体的地震响应小于自由场模型在相同地震动下的土体变形.而整体强制反应位移法由于其施加等效地震荷载的方式，计算所得到的结构变形更加接近自由场土层变形.整体强制反应位移法在计算结构变形时的误差稍大于计算结构内力时所得误差.在地震动强度为0.1g,0.2g,0.4g情况下，侧墙各点的平均误差分别为44.6%,42.6%,43.6%；中柱各点的平均误差分别为48.8%,44.7%,44.6%.

3　整体强制反应位移法的特点

从计算模型来看，一方面整体强制反应位移法使用土体-结构相互作用模型，能够更好地模拟地震作用下周围土层对结构的约束作用，同时省去了反应位移法等荷载结构法确定地基弹簧系数带来的困难；另一方面相对强制反应位移法而言，将最不利地层变形施加到整个地层有限元模型上，能够准确地将地震作用下的地层应变传递到结构上，而不会产生由模型边界向模型内部衰减的情况.

从计算参数的选取来看，整体强制反应位移法选用自由场地震反应分析得到的土层变形作为加载形式，相比于反应加速度法等选用土层水平惯性加速度作为施加的外荷载更加符合地下结构的震害机理.

从计算工作量上看，反应位移法地基弹簧系数的准确确定需要耗费大量计算成本；反应加速度法需要施加沿土层深度分布的土层惯性加速度.而大多数情况下加速度-深度分布曲线较位移-深度分布曲线复杂得多，难以拟合，只能对位于同一深度的土层单元及结构单元逐层施加加速度，实际操作相对繁琐.位移-深度分布曲线较简单，可以拟合成相应函数后施加到拟静力模型上，非常方便；另外计算过程中发现模型施加位移的计算收敛性好，计算速度快.总体来讲，整体强制反应位移法较绝大多数抗震设计方法都更加简便、易于实现.

4　结论

(1) 结构抗震设计应该基于结构在地震作用下的受力机制是过去人们在不断的抗震设计研究中积累的经验.地下结构所受地震作用主要来自于周围地层的变形，且结构自身惯性力影响较小可忽略，这是地下结构与地上结构地震响应特征的主要区别.

(2) 传统的强制反应位移法仅仅将土层变形施加于土体-结构模型的边界上，致使土层变形不能有效作用于土层内部的地下结构.整体强制反应位移法在建立土体-结构相互作用模型的基础上将地震引起的地层变形施加于整个土层单元上.经验算，该方法能够有效计算结构在自重以及地震作用下的结构内力，在地震动强度为0.1g，0.2g，0.4g情况下，内力误差总体在5%～15%之间.

(3) 该方法概念清晰，实际实施步骤较大多数抗震设计方法更加简单方便.由于采用了位移的加载方式在实际有限元计算中稳定性好，易收敛，适合工程设计应用.

[1]袁勇，柳 献，禹海涛,等. 汶川地震隧道震害调查与思考[R]. 上海：同济大学，2008.

YUAN Yong，LIU Xian，YU Haitao，etal. Tunnel damage Investigation and reflection in Wenchuan Earthquake[R]. Shanghai：Tongji University，2008.

[2] 禹海涛，袁勇，张中杰,等. 反应位移法在复杂地下结构抗震中的应用[J]. 地下空间与工程学报，2011，7(5)：857.

YU Haitao，YUAN Yong，ZHANG Zhongjie，etal. Application of response displacement method on seismic design of a complex underground structure[J]. Chinese Journal of Underground Space and Engineering, 2011，7(5)：857.

[3] 刘晶波，王文晖，赵冬冬,等. 地下结构抗震分析的整体式反应位移法[J]. 岩石力学与工程学报，2013，32(8)：1618.

LIU Jingbo，WANG Wenhui，ZHAO Dongdong，etal. Integral response deformation method for seismic analysis of underground structure[J]. Chinese Journal of Rock Mechanics and Engineering，2013，32(8)：1618.

[4]陶连金，王文沛，张波,等. 地铁地下结构抗震设计方法差异性规律研究[J]. 土木工程学报，2012，45(12)：170.

TAO Lianjin，WANG Wenpei，ZHANG Bo，etal. Difference law study of seismic design methods for subway structures[J]. China Civil Engineering Journal，2012，45(12)：170.

[5]刘晶波，刘祥庆，薛颖亮. 地下结构抗震分析与设计的Pushover方法适用性研究[J]. 工程力学，2009，26(1)：49.

LIU Jingbo，LIU Xiangqing，XUE Yingliang. Study on applicability of a pushover analysis method for seismic analysis and design of underground structures[J]. Engineering Mechanics, 2009，26(1)：49.

[6]赵冬冬. 城市地铁地下结构地震反应的试验研究与数值模拟[D]. 北京：清华大学，2013.

ZHAO Dongdong. Experimental study and numerical simulation on seismic response of urban underground subway structures[D]. Beijing：Tsinghua University，2013.

[7]Akira T. A study on seismic analysis methods in the cross section of underground structures using static finite element method[J]. Structural Engineering & Earthquake Engineering，2005，122(1)：41.

[8]付鹏程. 地铁地下结构震动变形的实用评价方法研究[D]. 北京：清华大学，2004.

FU Pengcheng. Simplified methods for evaluating seismic deformation of metro underground structures considering seismic interaction[D].Beijing：Tsinghua University，2004.

[9]Hamada M，Sugihara Y，Shiba Y，etal. Observation and study on dynamic behavior of rock cavern during earthquake[J]. Journal of JSCE, 1989，341：187.

[10]Katayama I. Studies on fundamental problems in seismic design analyses of critical structures and facilities[D]. Kyoto：Kyoto University，1990.

[11]李彬. 地铁地下结构抗震理论分析与应用研究[D]. 北京：清华大学，2005.

LI Bin. Theoretical analysis of seismic response of underground subway structures and it’s application[D]. Beijing：Tsinghua University，2005.

[12]林皋，梁青槐. 地下结构的抗震设计[J]. 土木工程学报，1996，29(1)：15.

LIN Gao，LIANG Qinghuai. Seismic design of underground structures[J]. China Civil Engineering Journal，1996，29(1)：15.

[13]Idriss I M，Sun J I. User's manual for SHAKE91：A computer program for conducting equivalent linear seismic response analysis of horizontally layered soil deposits[M]. Davis：University of California， Davis, 1992.

[14]上海市城乡建设和交通委员会，上海市建筑建材业市场管理总站. DG/TJ 08-2064—2009上海市地下铁道建筑结构抗震设计规范[S]. 上海：出版单位不祥，2009.

Shanghai Urban and Rural Construction and Transportation Commission，Shanghai Building Materials Industry Market Management Station. DG/TJ 08-2064—2009 Code for seismic design of subway structures in Shanghai[S]. Shanghai: [s.n.]，2009.

[15]李新星，陈鸿，陈正杰. 地铁车站结构抗震设计方法的适用性研究[J]. 土木工程学报，2014，47(2)：322.

LI Xinxing，CHEN Hong，CHEN Zhengjie. Study on applicability of design method for seismic analysis of subway station[J]. China Civil Engineering Journal，2014,47(2)：322.

Integral Forced Displacement Method for Seismic Design of Underground Structures

CHEN Zhiyi1,2, TAN Zhong’ao2, LOU Menglin1

(1. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 2. College of Civil Engineering, Tongji University, Shanghai 200092, China)

The internal forces of underground structures in an earthquake are controlled by the seismic deformation of surrounding soils. Based on the forced displacement method for seismic design of underground structures, a novel seismic design method, named the integral forced displacement method, was proposed. The ground response deformation was applied to the finite element model of integral soil in this method to simulate seismic loading. Taking a subway station in Shanghai as an example, the implementation procedure and special features were introduced. By comparing with dynamic time history analysis results，the validity and accuracy of the proposed method was verified. The results show that the design concept of integral forced displacement method well agrees with the earthquake damage mechanism of underground structures, and the method is suitable for seismic analysis and design of underground structures in practice.

underground structure； earthquake damage characteristic； integral forced displacement method； seismic analysis and design

2015-08-04

国家自然科学基金(51278524)

陈之毅(1977—)，女，副教授，博士生导师，工学博士，主要研究方向为地下结构抗震. E-mail：zhiyichen@tongji.edu.cn

TU921

A