颗粒相壁面条件对非球形颗粒流动影响的数值模拟

华蕾娜，赵虎，2，李军，王军武，朱庆山

（1中国科学院过程工程研究所多相复杂系统国家重点实验室，北京 100190；2中国科学院大学，北京 100049）

颗粒相壁面条件对非球形颗粒流动影响的数值模拟

华蕾娜1，赵虎1，2，李军1，王军武1，朱庆山1

（1中国科学院过程工程研究所多相复杂系统国家重点实验室，北京 100190；2中国科学院大学，北京 100049）

采用双流体模型对设置竖直隔板的气固密相流化床中非球形颗粒的运动进行了模拟，颗粒形状的影响由相间曳力模型考虑，重点考察壁面处颗粒边界条件的影响。同时进行了实验室规模三维流化床的流化实验，以验证模型的有效性。通过压降轴向分布、颗粒浓度径向分布以及物料出口处颗粒质量流率功率谱估计等定量分析，结果表明：对不设置内构件的自由床，壁面反射系数对系统宏观流动特性影响较小，而对壁面处局部颗粒运动影响较大；对壁面面积大幅增加的内构件床，壁面反射系数可显著改变气体和颗粒的运动特征，取值需控制在适当范围内。

两相流；流化床；内构件；非球形颗粒；计算流体力学；壁面边界条件

引　言

形状非球形是自然界和工业生产中颗粒普遍存在的一种物性，并会显著改变气固系统中颗粒的动力学行为。为了简化问题，大部分实验室规模的实验均采用人造球形颗粒，如玻璃珠；数学分析时对颗粒做人为球形化处理，以利用标准球形颗粒较为成熟的研究成果。但已有研究表明，颗粒形状的非规则性会大大提高颗粒运动的复杂程度：对于单颗粒，颗粒形状和来流朝向会增强其曳力和升力［1］；对于多颗粒，非球形气固流化系统会产生较低的初始流化气速［2］或较高的压降［3］。因此，考察非球形颗粒在气固流化床中的流动特性具有重要的学术研究意义和工业应用价值。

考虑颗粒形状影响的 CFD模拟在颗粒轨道模型（CFD-DEM）中获得了较好的发展，而在欧拉双流体模型中研究较少。DEM通过跟踪每个颗粒的运动轨迹，直接得到颗粒的拉格朗日坐标和速度，并通过修正相间曳力［4］和颗粒碰撞几何关系等可模拟非球形颗粒在密相床中的流化行为［5］。然而由于对计算量和算法需求较高，目前DEM研究多局限于二维、小计算区域、低颗粒浓度、简单颗粒形状等问题的模拟［6］。与此相反，将颗粒视为拟流体的双流体模型在上述几方面表现出独特的优势，但由于颗粒形状无法像DEM那样直观处理，只能通过相间曳力和固相应力等方式间接考虑，所以采用双流体模型研究非球形颗粒的工作不多。Peirano等［7］通过最大堆积固含率和颗粒弛豫时间两个参数研究了颗粒球形度的影响，但未详细给出如何通过球形度修正气固相间曳力。

内构件是气固流化系统增强气固接触效率和改善流化质量的一种重要手段，可有效提高产品选择性和转化率［8］。彭迎彬等［9］和郝志刚等［10］采用实验手段研究了进料速率、流化气速等操作条件对装有垂直或水平构件密相床中颗粒停留时间的影响。刘英杰等［11］对人字型挡板、盘环型挡板和两段环流等3种形式FCC汽提器内的气固流动和混合情况进行了模拟研究。上述结果均表明，内构件可明显改变颗粒在床内的流动模式。在CFD模拟中，内构件的添加会增加壁面面积，从而使壁面边界条件的处理变得尤为重要。双流体模型广泛采用 Johnson-Jackson条件来描述壁面与颗粒的相互作用，所涉及的参数中颗粒-壁面碰撞恢复系数影响较小，而壁面反射系数的影响却不可忽视［12］。目前，壁面反射系数很难通过实验方法测量，模拟中一般由两种途径获得：① 建立与颗粒-壁面碰撞和壁面周围流场有关的关联式，将壁面反射系数的不确定性转移到颗粒-壁面摩擦系数等［13］；② 比较模拟结果与实验数据来获得最优值。方法②简单有效，但在不同流化系统中壁面反射系数的最优值不同且差异显著，比如鼓泡床中取0.5［14］，湍动床中取0.001［15］，而提升管的快速流态化则建议为近似全滑移（接近于0）［16］。

本研究拟采用双流体模型求解置有垂直隔板的连续进出料稠密气固流化床。为了考虑颗粒形状的影响，此处将作者以前发展的相间曳力模型［17］推广到带内构件的连续流化床中，重点考察颗粒与壁面边界设置对两相流动的影响，并通过模拟结果与实验数据的比较验证了模型的有效性。

1　实验与测量

图1　实验装置示意图Fig.1　Schematic diagram of experimental apparatus （unit: mm）

图1为连续进出料操作气固流化床实验装置的二维示意图，主要由主床体、双风室、竖直隔板、物料进口段和物料出口段组成。主床体尺寸为 120 mm（长）×60 mm（宽）×500 mm（高），物料进口段和出口段为直径60 mm的圆管，材质均为透明有机玻璃。颗粒由螺旋给料机且经流化密封阀进入物料进口段，然后进入主床体，在流化气速作用下经由3块竖直隔板流动、混合，最后由物料出口段流出。颗粒流动路径见图中箭头所示。颗粒进料速率为5.33 g·s-1。流化气速分别为0.4和0.45 m·s-1，Ug/Um f分别为4.2和4.7。通过实验观测发现对于不设置隔板的自由床，流域介于鼓泡床和节涌。实验中利用压力传感器对自由床和内构件床分别测量了轴向的压降分布。

流化的物料为碳酸钙颗粒，密度为 3135 kg·m-3，粒径为341 μm。颗粒形状呈典型的非规则特征，具体形态如图2所示。由Ergun公式可估算颗粒球形度为 0.36，具体计算流程见文献［17］第2.1.3部分。经气速-压降实验测得该颗粒初始流化气速Um f为0.095 m·s-1，初始流化固含率εsm f为0.6305。

图2　30倍电镜下的颗粒形态Fig.2　Shape of particles observed by scanning electron m icroscope

2　数学模型与设置

2.1双流体模型

气固系统双流体模型的控制方程组分别为气相、固相的质量守恒和动量守恒方程

式中，ρg、μg和ρs分别为气体密度、黏度和颗粒密度；g为重力加速度；εg、εs、ug、us和p为待求变量。固相压力ps、固相剪切和体积黏度系数μs、λs采用颗粒动理论封闭，而ps和μs中的颗粒摩擦应力采用Schaeffer模型。在不失精度的前提下为了节省计算量，求解的颗粒温度方程为代数形式。气固相间曳力在颗粒受力分析中占据着重要的位置，因此合理的曳力估计对准确预测颗粒流动非常关键。考虑颗粒非球形特征且适用于双流体模型的曳力模型较少，此处采用作者前期工作提出的相间曳力系数β关联式［17］

式中，ψ为球形度；dn和dv分别为等投影面积球当量直径和等体积球当量直径；D为流化床水力直径。对于本文所研究的颗粒，由于颗粒形状极其不规则并且具有一定粒径分布，dn和dv的测量非常困难。为了简化问题，dn和 dv均取为测量的颗粒Sauter平均直径dp。该关联式在不设置隔板且无颗粒进出的自由床中获得了较好的计算结果［17］，此处将其应用于图1中设置竖直隔板的连续床。

2.2模拟设置

为了减少计算量，对图1中实验装置的物料进出口段进行了简化：实验可观测到颗粒主要顺着进料管管壁滑入主床体，实际只占用进料管一小部分，故进口段取20 mm×20 mm截面；而在出口段由于颗粒会因气泡抛洒被大量甩入出料管，则出口段形状和尺寸与实际装置保持一致。经测试单个网格尺寸为12倍粒径时可达网格无关解，则对三维模拟自由床网格总数为70698个，有内构件床网格总数为63025个。时间步长取5.0×10-4s，计算过程稳定。本工作应用商业软件Ansys 15.0进行计算。底部气体入口和物料进口为给定速度边界，顶部出口和物料出口为压力边界。在物料进口处设定固含率为0.2，并根据进料速率计算颗粒速度。气相在壁面处设置为无滑移条件，而使用Johnson-Jackson条件处理固相的壁面情况。其他参数设置包括：颗粒-颗粒碰撞恢复系数取0.99，颗粒摩擦应力启用固含率为εsm f，颗粒最大堆积固含率取实验测量值0.4558。初始时刻，两相速度为零，颗粒堆积高度为0.191 m，堆积固含率根据全床总压降测量值估计。需要注意的是，由于为连续进出料系统，此处初始值的设定并不影响最终计算结果，但会影响系统达稳定的时间。计算中通过监测全床体积平均固含率随时间的变化来判断系统是否达稳定，取该量变化平稳后50 s做时均分析。

本文研究的流化床中装有3块竖直隔板，而且隔板尺寸较大，这使得边壁面积大幅增加。与自由床相比，图1中内构件床的有效壁面面积增加值超过80%，因此固相壁面边界条件的处理十分关键。Johnson-Jackson条件通过引入壁面反射系数φ来反映颗粒和壁面因碰撞产生的动量传递，取值范围为0～1.0。当φ=0时，壁面被视为光滑平面，颗粒为自由滑移；当φ=1.0时，则壁面粗糙，颗粒为无滑移。考虑到文献中不同流域φ最优值跨度较大，本文设φ分别为0、0.0005、0.005、0.05、0.5和1.0，以考察其效果。

3　结果与讨论

3.1壁面条件对自由床的影响

图3给出了0.4 m·s-1气速时φ取不同值时均压降的轴向分布情况。可以看出，区别较小并均与实验数据吻合较好。对于0和1.0两种极端情况，统计全床体积平均固含率的时均值：φ=0时为0.143；φ=1.0时为0.146。统计床层总压降（测量区间为距离分布板 0.012～0.412 m）的时均值：φ=0时为2216 Pa；φ=1.0时为2312 Pa，实测值为2240 Pa。上述数据再次表明，对于不设置隔板的自由床，固相壁面边界条件对流化床宏观流动特性的影响较为有限。

图3　气速为0.4 m·s-1时壁面反射系数对自由床压降轴向分布的影响Fig.3　Effect of specularity coefficient on axial profile of time-averaged pressure in bed w ithout internals when Ug=0.4 m·s-1

图4给出了气速为0.4 m·s-1时高度为0.1和0.2 m处颗粒浓度时均值沿三维床体宽度方向的径向分布。沿床体深度方向的分布类似，简明起见此处未给出。可以清晰地看出，在两侧近壁处［x/L=±（0.8～1.0）范围内］颗粒浓度分布受壁面反射系数影响较大，甚至改变了递增或递减等变化方向。该特点直接导致了颗粒浓度分布形式的改变：φ=0时两个高度处颗粒浓度呈抛物线分布，而φ=1.0时则呈不同程度的双峰分布，这意味着气泡在床内的运动路径发生了变化。该结果与鼓泡床等密相气固流化系统研究结论保持一致［18］。图3中的压降轴向分布经过了截面面积加权平均处理，所以大大淡化了颗粒动力学特征在壁面处的区别。综上所述，壁面反射系数对自由床的宏观流动特性影响较小，但会改变颗粒在壁面附近的局部运动特性，比如浓度分布或速度方向。

图4　气速为0.4 m·s-1时壁面反射系数对自由床颗粒浓度径向分布的影响Fig.4　Effect of specularity coefficient on radial profile of time-averaged solids concentration in bed w ithout internals at two heights when Ug=0.4 m·s-1

3.2壁面条件对内构件床的影响

图5给出了0.4和0.45 m·s-1工况下φ分别取0、0.0005、0.005、0.05、0.5和1.0时内构件床中压降的轴向分布。与自由床相比，壁面反射系数对内构件床中压降产生了显著的影响：随着φ的增加，计算值与实验数据的吻合程度越来越好；当φ取值大于0.05时，其影响程度开始大幅减弱。表1列出了0.4 m·s-1工况φ取不同值时流化床达到稳定运行阶段全床体积平均固含率和床层总压降（测量区间为距离分布板0.062～0.412 m）的计算值，对应的压降测量值为2057 Pa。在实验测量中，内构件床被3块竖直隔板分成3个区，压力传感器只布置在中间区，而计算取截面面积加权平均值，因此虽然表1中内构件床压降计算值与实验值的吻合程度不如自由床，但尚在合理范围内。表1中的数据表明，φ的取值可显著改变内构件床中的存料量，当φ取较大值时床内存料量将增多。这是因为颗粒在壁面处的摩擦增大会导致更多颗粒停留在床内，而内构件床由于壁面面积较大累积效果更为突出。

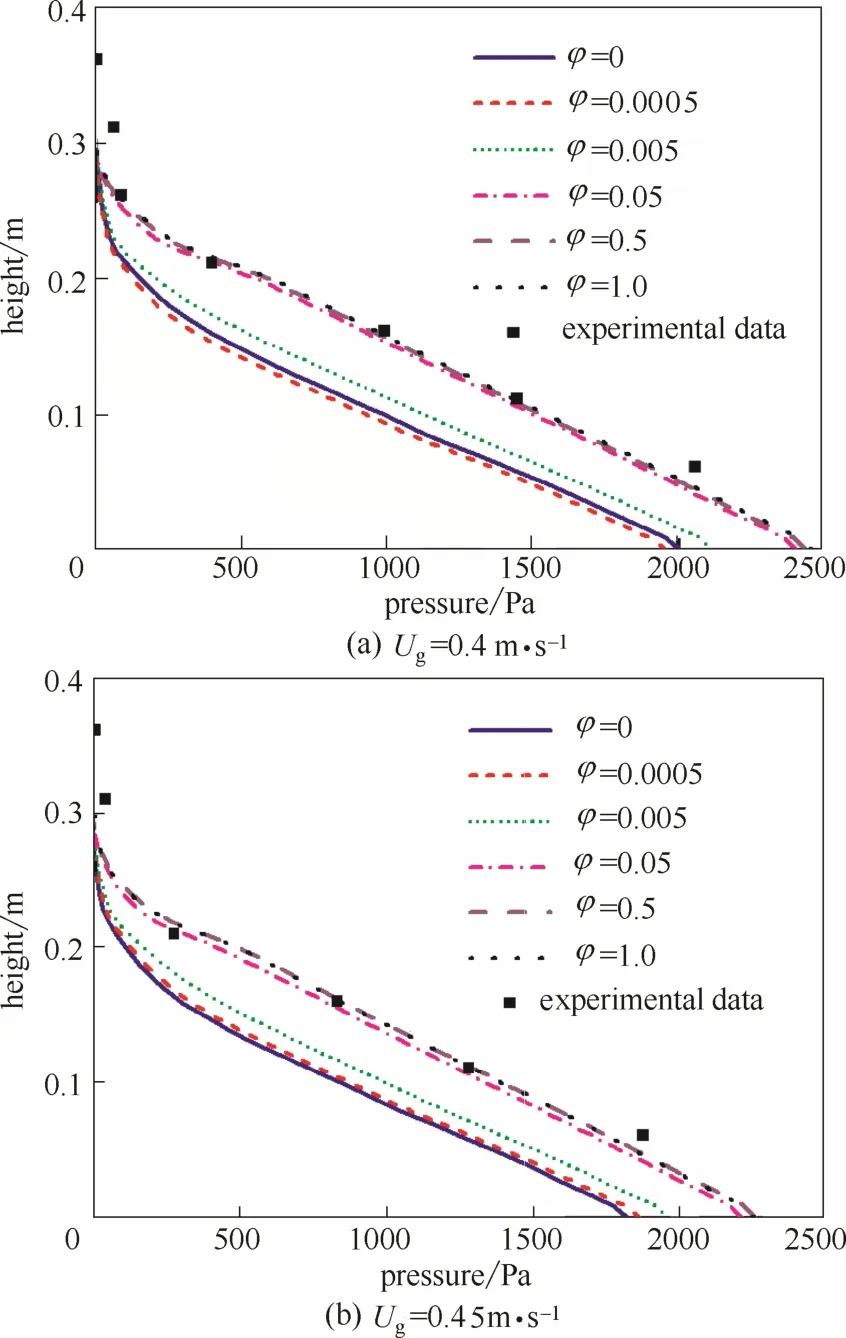
图5　不同气速时壁面反射系数对内构件床压降轴向分布的影响Fig.5　Effect of specularity coefficient on axial profile of time-averaged pressure in bed w ith internals

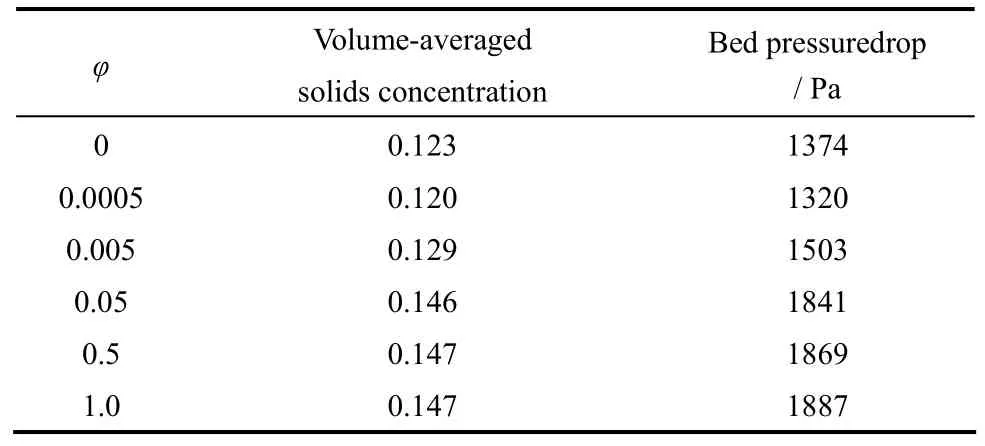
表1　气速为0.4 m·s-1时内构件床中壁面反射系数对体积平均固含率和床层压降（计算区间为距离分布板0.062～0.412 m）的影响Table 1　Effect of specularity coefficient on volume-averaged solids concentration and bedpressuredrop （measured from 0.062 m to 0.412 m above gas distributor） in bed w ith internals when Ug=0.4 m·s-1

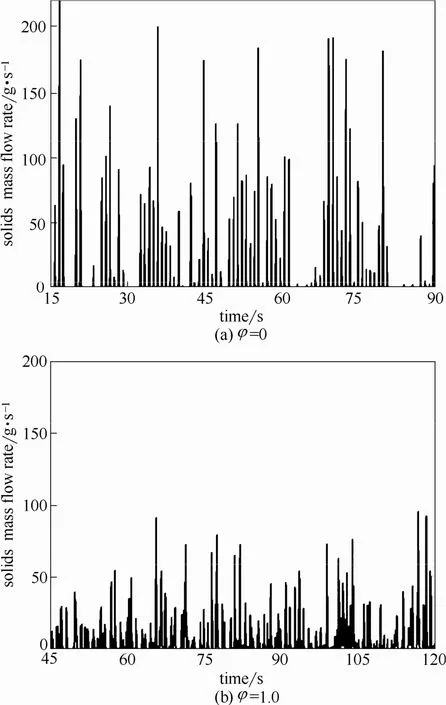
图6　气速为0.4 m·s-1时内构件床物料出口处颗粒质量流率的变化Fig.6　Solids mass flow rate at outlet of bed w ith internals when Ug=0.4 m·s-1

对物料出口处颗粒质量流率进行频域分析是了解连续流动床内颗粒流动特点的有效手段之一。在本文两个计算工况下，实验可观测到床内存在着明显的气泡行为。这将导致颗粒在物料出口处的溢出并非连续：当气泡上升到床层表面破裂时，会抛洒一部分颗粒并促使大量颗粒排出，而当气泡在床层内部移动、聚并时，颗粒通过进料口持续进料以弥补床内颗粒的缺失，则此时间段内颗粒流出量较少。以φ=0和1.0为例，图6所示为0.4 m·s-1工况物料出口处75 s内颗粒质量流率的变化情况（系统已达到稳定阶段），可发现两者均具有典型的间歇性特征，定性上与实验观测一致。另外，φ取0.0005、0.005时与取0时的结果类似，而φ取0.05、0.5时与取1.0时的结果类似，正如图6中所示两者又表现出不同的特点：前者单次出料量较大而出料时间间隔较长；后者单次出料量较小而出料时间间隔较短。这表明壁面反射系数的取值有效改变了内构件床中的颗粒运动行为。

图7　不同气速时内构件床物料出口处颗粒质量流率的功率谱分布Fig.7　Power spectral density of solids mass flow rate at outlet of bed with internals

图8　气速为0.4 m·s-1时系统运行稳定阶段内构件床中颗粒浓度的分布Fig.8　Contours of solids concentration in bed w ith internals when Ug= 0.4 m·s-1

图7所示为两个气速下不同φ取值时物料出口处颗粒质量流率时间序列的功率谱估计结果，为图6物理量的定量分析。本文采用韦尔奇（Welch）方法进行估计，具体参数为：取计算稳定阶段50 s数据，采样频率设为200 Hz，则共产生10000个数据点；将全部数据点分成6段，每段可重叠10%；对每段数据使用Hamm ing窗函数，并做傅里叶变换，最后取功率谱的均值。对大部分气固流化系统，主频一般分布在1～5 Hz，数据采样10 s即可满足样本长度要求［19］，则上述采样合理。图7中在频率为0处功率谱存在着一个较大值，这是因为当流化床达到稳定状态时，物料出口处颗粒质量流率在一个较长时间段内的时均值应与颗粒进料速率相同，即为5.33 g·s-1，而该常数在功率谱中即表现为频率等于0处的直流分量，在下述分析中可不予考虑。图中可清楚看出，随着φ的增加，功率谱呈现出不同的特征：当φ等于0或较小时，在0～5 Hz范围内规律地分布着4个尖峰；当φ较大或等于1.0时，4个尖峰显著减弱并逐渐消失。两个气速工况的计算结果均具有该特点。以往研究者通过分析气固密相流化床中压强时间序列信号指出，单个大气泡的功率谱表现为峰值高和跨度窄，而多个小气泡的功率谱表现为峰值低和跨度宽［20-21］。以此为基础，可尝试解释图7中的现象：4个尖峰代表着内构件床中由3块竖直隔板划分的4块区域，尖峰量值不同则表示每块区域表现出不同的流动特性。当φ取值较小时，尖峰峰值高跨度窄，这表明气泡尺寸较大，而由两块竖直隔板构成的区域较为狭窄，可能促使发生局部节涌。当φ取值较大时，尖峰峰值低跨度宽，这表明气泡尺寸较小，但数量可能较多。从壁面模拟条件来讲，φ值小意味着颗粒在边壁处容易滑动，更利于大气泡的形成；而φ值大则颗粒倾向于粘附在边壁上，颗粒在壁面附近移动困难，因而在由两块竖直隔板形成的狭小区域内不利于气泡的产生。

图8为0.4 m·s-1气速下φ取不同值时70 s时刻内构件床中颗粒浓度的分布情况。可以看出，当φ值较小时（比如0、0.0005和0.005）由3块竖直隔板构成的4块区域中一部分出现了典型的节涌现象，形成了尺寸较大的气栓；而当 φ取 0.05、0.5 和1.0时，4块区域均匀分布着小气泡，并且各区域中床层表面基本持平。图8中的定性认识与图7中的定量分析保持一致，并且很好解释了图7中的变化规律。在实验中，通过流化床透明前壁可观测到竖直隔板可有效分解分布板附近产生的大气泡，在隔板间形成众多小气泡，而且各个隔板间床面与物料出口处基本保持水平。可以看出，图8中当φ取0.05、0.5和1.0时的结果较为符合实验观测，这表明本文计算工况下φ取较大值时可合理地捕捉内构件床中的颗粒动力学行为。

4　结　论

采用双流体模型研究了设有3块竖直隔板内构件的气固密相床中非球形颗粒的流态化行为，重点探讨了颗粒壁面边界条件的影响。通过设置不同壁面反射系数取值，发现自由床中宏观流动特性对该系数并不敏感，但在壁面附近颗粒行为会有显著改变；而由于壁面面积的大幅增加，该系数对内构件床存料量和气体、颗粒流动特性有重要影响。通过压降分布、物料出口处颗粒质量流率的功率谱估计等定量分析，以及与相关实测数据的对比，可认为在本文计算条件下壁面反射系数取较大值时，例如本文研究范围内的0.05、0.5或1.0，可较好地定量和定性反映实验观测现象。壁面反射系数取值的困难和不确定性给双流体模型的广泛应用带来了阻力，深入剖析颗粒在壁面处的运动机制并提出有效计算壁面反射系数的模型是未来解决该问题的一个重要方向。

符号说明

Cd0——单颗粒曳力系数

D ——床水力直径，m

dn——等投影面积球当量直径，m

dp——颗粒粒径，m

dv——等体积球当量直径，m

g ——重力加速度，m·s-2

I ——单位矩阵

K1，K2——形状参数

p——气相压强，Pa

ps——固相压强，Pa

Res——颗粒Reynolds数

Ug——流化气速，m·s-1

Um f——初始流化气速，m·s-1

ug， us——分别为气相和固相速度，m·s-1

β——气固相间曳力系数，kg·m-3·s-1

εg， εs——分别为气相和固相体积分数

εsm f——初始流化固含率

μg， μs， λs——分别为气体黏度系数、固相剪切和体积

黏度系数，Pa·s

ρg， ρs——分别为气体和颗粒密度，kg·m-3

τg， τs——分别为气相和固相应力，Pa

φ——壁面反射系数

φgs——反正切函数

ψ——球形度

下角标

g——气相

s——固相

References

［1］ 由长福， 祁海鹰， 徐旭常. 气固两相流动中非球形颗粒所受曳力的数值研究［J］. 化工学报， 2003， 54（2）: 188-191.

YOU C， QI H Y， XU X C. Numerical simulation of drag force on non-spherical particle in gas-particle two-phase flow ［J］. Journal of Chem ical Industry and Engineering （China）， 2003， 54（2）: 188-191.

［2］ ZHOU Z Y， PINSON D， ZOU R P， et al. Discrete particle simulation of gas fluidization of ellipsoidal particles ［J］. Chem ical Engineering Science， 2011， 66（23）: 6128-6145.

［3］ RODRIGUES S S， FORRET A， MONTJOVET F， et al. Riser hydrodynam ic study w ith different Group B powders ［J］. Powder Technology， 2015， 272: 300-308.

［4］ HÖLZER A， SOMMERFELD M. New simple correlation formula for the drag coefficient of non-spherical particles［J］. Powder Technology，2008， 184（3）: 361-365.

［5］ ZHONG W Q， ZHANG Y， JIN B S， et al. Discrete element method simulation of cylinder-shaped particle flow in a gas-solid fluidized bed ［J］. Chem ical Engineering & Technology， 2009， 32（3）: 386-391.

［6］ SHERRITT R G， CHAOUKI J， MEHROTRA A K， et al. Axial dispersion in the three-dimensional m ixing of particles in a rotating drum reactor ［J］. Chem ical Engineering Science， 2003， 58（2）: 401-415.

［7］ PEIRANO E， DELLOUME V， LECKNER B. Two- or three-dimensional simulations of turbulent gas-solid flows applied to fluidization ［J］. Chem ical Engineering Science， 2001， 56（16）: 4787-4799.

［8］ 金涌， 俞芷青， 张礼， 等. 流化床反应器塔型内构件的研究［J］. 化工学报， 1980， 41（2）: 117-128.

JIN Y， YU Z Q， ZHANG L， et al. A study of pagoda type vertical internal baffle in gas-fluidized bed ［J］. Journal of Chem ical Industry and Engineering （China）， 1980， 41（2）: 117-128.

［9］ 彭迎彬， 李海广， 李保卫， 等. 置有竖直隔板鼓泡流化床物料停留时间［J］. 科学技术与工程， 2015， 15（21）: 38-47.

PENG Y B， LI H G， LI B W， et al. Particle residence time in a bubbling fluidized bed w ith inner-vertical partition plate ［J］. Science Technology and Engineering， 2015， 15（21）: 38-47.

［10］ 郝志刚， 朱庆山， 李洪钟. 内构件流化床内颗粒停留时间分布及压降的研究［J］. 过程工程学报， 2006， 6（2）: 359-363.

HAO Z G， ZHU Q S， LI H Z. Particle residence time and pressure drop in a fluidized bed w ith internals ［J］. The Chinese Journal of Process Engineering， 2006， 6（2）: 359-363.

［11］ 刘英杰， 杨基和， 蓝兴英， 等. 工业RFCC汽提段内颗粒混合情况的CFD模拟［J］. 化学反应工程与工艺， 2012， 28（3）: 213-219.

LIU Y J， YANG J H， LAN X Y， et al. CFD simulation of solid residence time distribution in industrial RFCC strippers ［J］. Chemical Reaction Engineering and Technology， 2012， 28（3）: 213-219.

［12］ LAN X Y， XU C M， GAO J S， et al. Influence of solid-phase wall boundary condition on CFD simulation of spouted beds ［J］. Chemical Engineering Science， 2012， 69（1）: 419-430.

［13］ LI T W， BENYAHIA S. Evaluation of wall boundary condition parameters for gas-solids fluidized bed simulations ［J］. AIChE Journal， 2013， 59（10）: 3624-3632.

［14］ ALTANTZIS C， BATES R B， GHONIEM A F. 3D Eulerian modeling of thin rectangular gas-solid fluidized beds: estimation of the specularity coefficient and its effects on bubbling dynamics and circulation times ［J］. Powder Technology， 2015， 270: 256-270.

［15］ 卢竟蔓， 蓝兴英， 徐春明， 等. 壁面条件对FCC颗粒湍动床气固流动影响的模拟［J］. 化学反应工程与工艺， 2014， 30（1）: 57-62.

LU J M， LAN X Y， XU C M， et al. Numerical simulation on effect of wall boundary condition on gas-solid flow in FCC particles turbulent bed ［J］. Chemical Reaction Engineering and Technology， 2014， 30（1）: 57-62.

［16］ 周新宇， 高金森， 徐春明， 等. 颗粒相壁面条件对提升管内气固流动模拟的影响［J］. 化工学报， 2012， 63（4）: 1063-1069.

ZHOU X Y， GAO J S， XU C M， et al. Effect of solids phase wall boundary condition on simulation of gas-solids flow characteristics in riser ［J］. CIESC Journal， 2012， 63（4）: 1063-1069.

［17］ HUA L N， ZHAO H， LI J， et al. Eulerian-Eulerian simulation of irregular particles in dense gas-solid fluidized beds ［J］. Powder Technology， 2015， 284: 299-311.

［18］ LI T W， GRACE J， BI X T. Study of wall boundary condition in numerical simulations of bubbling fluidized beds ［J］. Powder Technology， 2010， 203（3）: 447-457.

［19］ JOHNSSON F， ZIJERVELD R C， SCHOUTEN J C， et al. Characterization of fluidization regimes by time-series analysis of pressure fluctuations ［J］. International Journal of Multiphase Flow，2000， 26（4）: 663-715.

［20］ ABBASI M， SOTUDEH-GHAREBAGH R， MOSTOUFI N， et al. Non-intrusive monitoring of bubbles in a gas-solid fluidized bed using vibration signature analysis ［J］. Powder Technology， 2009，196（3）: 278-285.

［21］ JAIBOON O-A， CHALERMSINSUWAN B， MEKASUT L， et al. Effect of flow pattern on power spectral density of pressure fluctuation in various fluidization regimes ［J］. Powder Technology，2013， 233: 215-226.

Numerical study of effect of particle wall boundary condition on fluidization of irregular particles

HUA Leina1， ZHAO Hu1，2， LI Jun1， WANG Junwu1， ZHU Qingshan1
（1State Key Laboratory of Multiphase Complex Systems， Institute of Process Engineering， Chinese Academy of Sciences，Beijing 100190， China；2University of Chinese Academy of Sciences， Beijing 100049， China）

The behavior of non-sphere particles in a gas-solid dense phase fluidized bed allocated w ith three vertical internals was simulated by the Eulerian two-fluid model. The effects of particle shapes were taken into account by an inter-phase drag model， and more effort was devoted to the effects of the boundary conditions of particles at walls. Meanwhile， experiments of a three dimensional lab-scale fluidized bed were conducted to provide available validation data. The quantitative analyses included axial profile of the pressure， radial profile of solids concentration， and power spectral density of particle mass flow rate at the bed outlet. It showed that specular reflection coefficient only affects the macroscopic behavior of the bed slightly， but the local particle motion near walls significantly for the bed w ithout internals. While for the bed w ith internals featuring a remarkable increase in wall area， specular reflection coefficient can significantly influence dynamics of gas and solids. Therefore， the value of specular reflection coefficient should be selected in an appropriate range for beds w ith internals， to predict the system reasonably.

two-phase flow； fluidized-bed； internals； particles w ith irregular shapes； CFD； wall boundary condition

date: 2016-03-31.

HUA Leina， lnhua@ipe.ac.cn

supported by the National Natural Science Foundation of China （21306202）， the National Basic Research Program of China （2012CB215003） and the State Key Laboratory of Multiphase Complex Systems， Institute of Process Engineering， Chinese Academy of Sciences （MPCS2012A02， MPCS2014A03）.

TQ 021.1

A

0438—1157（2016）08—3251—08

10.11949/j.issn.0438-1157.20160405

2016-03-31收到初稿，2016-05-04收到修改稿。

联系人及第一作者：华蕾娜（1980—），女，博士，副研究员。

国家自然科学基金项目（21306202）；国家重点基础研究发展计划项目（2012CB215003）；中国科学院过程工程研究所多相复杂系统国家重点实验室基金项目（MPCS2012A02，MPCS2014A03）。