Smith圆图理解和使用的几个关键问题

何思远, 贺菁菁, 黄冉冉, 张云华, 张兰

(武汉大学 电子信息学院， 湖北 武汉 430072)

Smith圆图理解和使用的几个关键问题

何思远, 贺菁菁, 黄冉冉, 张云华, 张兰

(武汉大学 电子信息学院， 湖北 武汉 430072)

Smith圆图由三个圆系构成，图形繁杂，是“微波技术”课程教学的重点和难点。笔者在教学过程中，结合内在物理现象的理解，将圆图分为三个层次逐层讲解相关内容，有助于学生们对圆图的深刻理解和熟练掌握。

Smith圆图；阻抗；反射系数

0 引言

Smith圆图是分析传输线工作状态的有力工具，也是“微波技术”课程教学的重点和难点。对于初次接触微波技术的学生来说，对Smith圆图理解起来难度颇大，主要体现在以下几个方面：①Smith圆图涉及到反射系数，阻抗，导纳三个圆系，是由很多圆周交织在一起的图形，线条较多，构成比较复杂，含有的信息也很丰富；②使用圆图求解传输线问题的过程中，传输线参量沿着传输线变换的过程需要动态映射到Smith圆图上，这种动态映射和变换较为复杂；③对圆图背后隐含的传输线上的物理现象和物理概念缺乏深入理解，比如波腹点、波节点的形成，四分之一波长阻抗变换，匹配点的意义等等[1]。这三个方面制约了学生对圆图的熟练使用。

针对上述问题，笔者在教学过程中，将圆图分为三个层次逐层讲解并分析传输线参量在传输线和圆图之间的映射关系。第一层，传输线和等反射系数圆之间的参量映射；第二层，反射系数和输入阻抗之间的映射；第三层，导纳圆图和阻抗圆图之间的映射。教学过程中，笔者还特别引导学生利用圆图对传输线上物理现象和过程进行解释。本文的教学方法在教学实践中起到了非常好的教学效果。

1 传输线和等反射系数圆互相映射

在圆图教学的起始，就应让学生认识到， Smith圆图是建立在反射系数的复平面基础之上的[2]，因此，首先介绍清楚传输线和等反射系数圆之间的参量映射，但此时不宜急于引入阻抗曲线，避免给学生理解第一层映射关系时带来不必要的困惑，等学生理解第一层次的映射之后，再对反射系数与阻抗之间的映射进行第二层次的介绍。

如图1所示，若设负载所在的位置z=0，从负载指向源的方向为z的正方向，则反射系数有如下关系式：

(1)

反射系数沿着传输线幅度不变，相位周期变化，而反射系数沿着等反射系数圆也具有相同的变化规律。传输线上每一个位置的反射系数，都可以通过等反射系数圆上相应一点的值读出。参量在传输线和等反射系数圆之间存在映射关系。为了理清该映射关系，还需要搞清楚两个问题：①反射系数变化周期在等反射系数圆和传输线上的呼应；②反射系数移动方向在等反射系数圆和传输线上的呼应。从反射系数的定义式，很容易得出问题的答案。反射系数沿着等反射系数圆顺时针转，对应反射系数相位减小，也就意味着式(1)中z的增加，也就是说在传输线上反射系数往源的方向移动。当圆图上反射系数转过一圈，相位变化2π，对应式(1)中2βz=2π，可以解出传输线上的周期为半波长。

笔者在教学时发现，学生对波节点和波腹点的确定有较大困难，原因就是缺乏对波腹和波节形成的物理概念的思考；反射波和入射波相干幅度增强即为波腹，此时两列波同相，对应反射系数相位为2π的整数倍，因此波腹分布在圆图的正实轴上[3]。反之，波节时，反射波与入射波反相，反射系数相位为2π的整数倍，因此波节分布在圆图的负实轴上。

图1 端接负载阻抗的传输线

2 反射系数和输入阻抗互相映射

圆图上同一点既可以读出反射系数，也可以读出阻抗值。圆图上归一化输入阻抗和反射系数之间的一一对应关系即本文论述的第二层映射，结合反射系数在圆图和传输线之间的第一层映射，实际上也描述了阻抗参量在圆图和传输线之间的映射。

驻波比的确定是求解传输线问题的一个关键。很多学生知道驻波比是圆图正半轴与等反射系数圆交点的归一化电阻值，但是不知道为什么这样确定。本文结合该点的物理意义，对驻波比的确定进行详细的介绍。圆图正半轴与等反射系数圆交点对应着电压波腹点，电流的波节点，因此输入阻抗在该点取得最大值。传输线上任意位置的电压和电流可以由下式给出：

V(z)=V+(z)+V-(z)=V+(z)[1+Γ(z)]

(2)

I(z)=I+(z)+I-(z)=I+(z)[1-Γ(z)]

(3)

由电压和电流之比可以得到输入阻抗：

(4)

在波腹点，反射系数为实数，又由于特性阻抗是实数，所以波腹点的归一化输入阻抗可以判断为实数，并且刚好是驻波比的值。

如何在阻抗圆图上通过阻抗点确定传输线上该点的导纳值是圆图应用的难点。为此，引导学生利用圆图解释传输线上λ/4阻抗变换现象[4]。

距离负载λ/4的传输线处，输入阻抗满足：

(5)

上式可写为

(6)

由此我们可以得出，l=λ/4位置的归一化输入阻抗值，是负载归一化阻抗值的倒数，也即负载阻抗相应的导纳值。上述阻抗变换现象，可以在圆图上进行解释。

从负载阻抗点出发，沿着等反射系数圆转过半圈，即对应着传输线上转过λ/4，由到达点读出的阻抗值，就是负载阻抗的倒数，也就是导纳值。需要注意的是，在由阻抗圆图确定导纳的过程中，并未引入导纳圆图的教学内容，这也是为了避免导纳圆图可能给学生带来不必要的困惑。

3 导纳圆图和阻抗圆图互相映射

阻抗圆图和导纳圆图在使用过程中非常容易混淆。首先，使用的原则就是“在什么山上唱什么歌”。作为阻抗圆图使用时，从图中读出的值就是阻抗值。作为导纳圆图使用时，图中读出的值就是导纳值。同一个圆图既可以看成是阻抗圆图，也可以看成是导纳圆图。两者之间的区别就在于反射系数不一样。阻抗圆图中反射系数实轴正半轴方向对应于导纳圆图反射系数实轴负半轴，阻抗圆图反射系数虚轴正半轴对应导纳圆图反射系数虚轴负半轴，如图2和图3所示。传输线上任一点，阻抗和反射系数一一对应，导纳和反射系数也一一对应，因此，阻抗圆图和导纳圆图之间的映射，可以通过反射系数相同来确定。

在上面四分之一波长阻抗变换的的圆图解释中，我们提出了在阻抗圆图上确定导纳点的方法，由此可知，阻抗圆图中A点阻抗参量对应的导纳参量为C点读出的阻抗值。

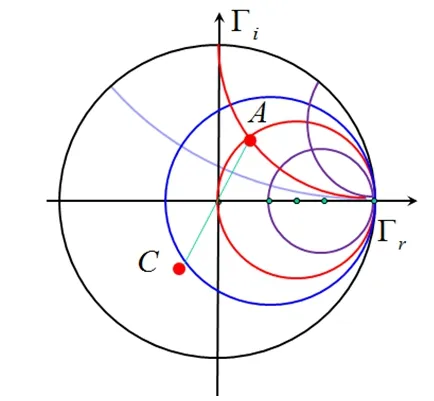
图2 阻抗圆图

图3 导纳圆图

那么如何从导纳圆图中，确定出导纳点，使得该点和阻抗圆图上的阻抗点，在传输线上对应的是同一个映射位置呢？在导纳圆图中，找到与阻抗圆图中A点反射系数相同的位置B点，该点即为阻抗圆图中A点所对应的导纳点。可以看出，C点与B在图形中是同一点，两种方法确定的导纳点是一样的[4]。

4 结语

Smith圆图是分析传输线工作状态的有效工具。对圆图的深刻理解和熟练掌握才能对微波电路中复杂传输线问题进行求解。本文梳理了圆图理解和使用的几个关键问题，提出了传输线参量在传输线和圆图之间映射关系的逐层分析教学方法，并将其应用于教学实践，取得了较好的教学效果。

[1] POZAR D M, 张肇仪. 微波工程[M]. 北京: 电子工业出版社，2006.

[2] 闫润卿，李英惠. 微波技术基础 [M]. 北京：北京理工大学出版社，2008.

[3] 梁昌洪，谢拥军，官伯然. 简明微波 [M]. 北京：高等教育出版社，2006.

[4] 褚庆昕, 涂治红, 王云. Smith 圆图形象化教学方法探讨 [J].南京：电气电子教学学报, 2009, 31(B11): 128-130.

[5] 李九生，叶强．“电磁场理论与微波技术”课程实践教学探索[J]．南京：电气电子教学学报，2008,30(4):63-64

Several Key Problems in Understanding and Using Smith Chart

HE Si-yuan，HE Jing-jing，HUANG Ran-ran，ZHANG Yun-hua，ZHANG Lan

(SchoolofElectronicInformation,WuhanUniversity,Wuhan430072,China)

In teaching of Microwave Technology course, Smith chart, which consists of three complicated circle systems, is the key and difficult point. The author divided the circle diagram into three levels to analyze the related contents step by step in the teaching process, which is helpful for deep understanding and mastering of Smith chart.

Smith chart; impedance; reflection coefficient

2016-01-22;

2016-05-08

何思远(1982-)，女，博士，副教授，主要从事雷达、计算电磁学的教学和研究工作。E-mail：siyuanhe@whu.edu.cn

G426

A

1008-0686(2016)05-0058-03