关于两个(p,q)型Fibonacci多项式乘积的研究

王　慧，王伟平

(浙江理工大学理学院，杭州 310018)



关于两个(p,q)型Fibonacci多项式乘积的研究

王慧，王伟平

(浙江理工大学理学院，杭州 310018)

利用组合数学的方法研究了两个(p,q)型Fibonacci多项式的乘积满足的恒等式、递推关系及生成函数，建立了两个(p,q)型Fibonacci多项式的乘积之和满足的递推关系及显式表达式，推广了Falcon的结论。此外，通过将所得的关于(p,q)型Fibonacci多项式序列的一般性结果应用到经典的Fibonacci多项式及Chebyshev多项式上，得到了很多新的组合恒等式。

(p,q)型Fibonacci多项式；(p,q)型Lucas多项式；生成函数；递推关系；组合恒等式

0　引　言

在组合数学中，很多特殊的组合序列都可以通过二阶的递推关系定义，例如Fibonacci数、Lucas数、Pell数、Fibonacci多项式、Lucas多项式等。这些序列在组合数学、数论、数值分析等学科中都有重要的应用。

定义(p,q)型Fibonacci多项式序列(un(x))和(p,q)型Lucas多项式序列(vn(x))为：

u0(x)=0，u1(x)=1，un(x)

=p(x)un-1(x)+q(x)un-2(x)，(n≥2)，

v0(x)=2，v1(x)=p(x)，vn(x)

=p(x)vn-1(x)+q(x)vn-2(x)，(n≥2).

很多特殊的多项式序列都是(p,q)型Fibonacci多项式序列以及(p,q)型Lucas多项式序列的特例(见表1)[1-4]。此外，若p(x)与q(x)都取非零实数，就得到著名的Lucas序列。例如，Fibonacci数、Lucas数等构成的二阶递推序列都是特殊的Lucas序列。

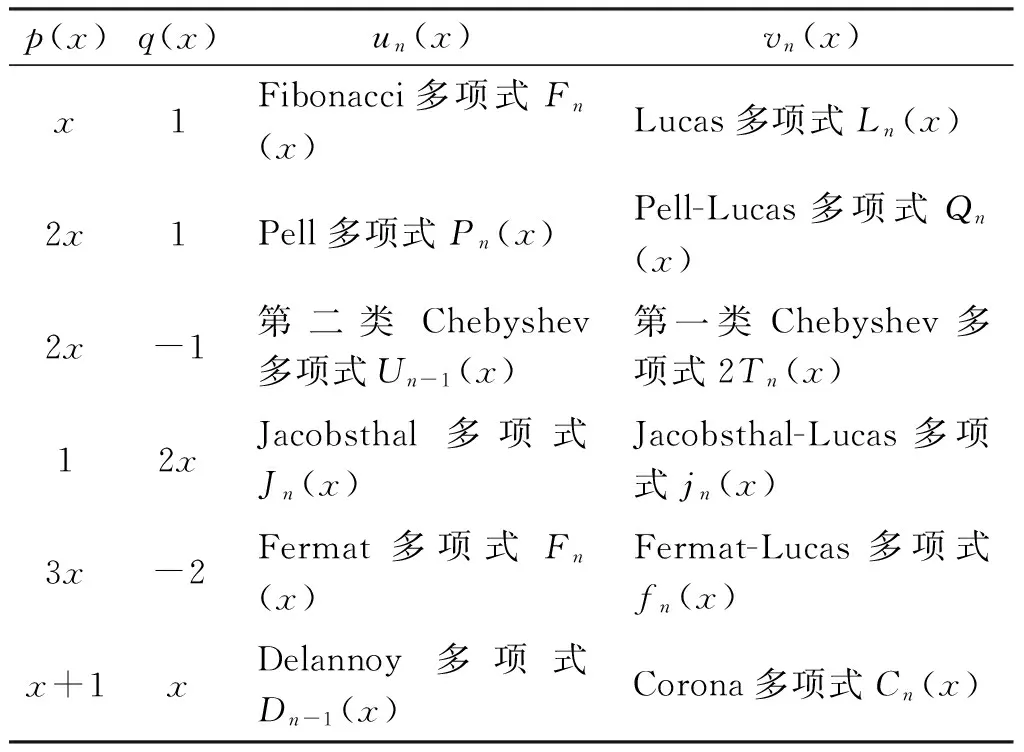
表1　 特殊的(p,q)型Fibonacci多项式和

由定义可以得到(p,q)型Fibonacci多项式序列(un(x))以及(p,q)型Lucas多项式序列(vn(x))的前几项：

u0(x)=0，u1(x)=1，u2(x)=p，

u3(x)=p2+q，u4(x)=p3+2pq，

v0(x)=2，v1(x)=p，v2(x)=p2+2q，

v3(x)=p3+3pq，v4(x)=p4+4p2q+2q2，

为简洁起见，本文将多项式p(x)简写成p, q(x)简写成q。如果令α和β为特征方程t2-pt-q=0的根，则：

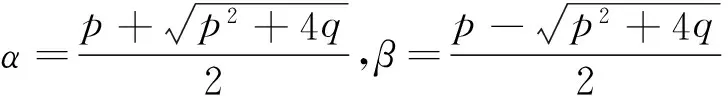
且α+β=p, αβ=-q，利用特征根α和β可以给出(un(x))和(vn(x))满足的Binet公式：

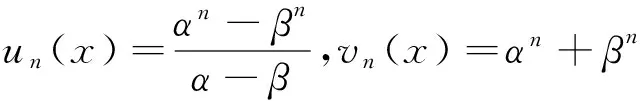
近年来，有关(p,q)型Fibonacci多项式序列和(p,q)型Lucas多项式序列的研究很多。例如：Lee等[1]研究了这些序列的一些基本性质及相关的矩阵；Wang[2]研究了这些序列满足的组合恒等式；He等[3]研究了更一般形式的满足二阶线性递推关系的数列与多项式序列，并且利用这些序列研究了某些代数方程和常微分方程的解的问题。其他研究可以参见一些相关的论文[4-6]。

Falcon[7]研究了两个k-Fibonacci数的乘积之和，其中k-Fibonacci数实际上也是(p,q)型Fibonacci多项式序列的特例，只要令p(x)=k, q(x)=1即可。本文将在Falcon[7]的工作的基础上，将数列推广到多项式序列，研究两个(p,q)型Fibonacci多项式的乘积满足的恒等式、递推关系及生成函数，并进一步研究两个(p,q)型Fibonacci多项式的乘积之和满足的递推关系及显式表达式，最后本文将所得的一般性结果应用到经典的Fibonacci多项式以及Chebyshev多项式上，建立了很多含Fibonacci多项式、Lucas多项式、第一类与第二类Chebyshev多项式的恒等式。

1　两个(p,q)型Fibonacci多项式的乘积

下面将研究两个Fibonacci多项式的乘积满足的恒等式和递推关系。

定理1(p,q)型Fibonacci多项式序列(un(x))满足如下恒等式：

um(x)un+1(x)-um+1(x)un(x)=

-(-q)mun-m(x)，(n≥m)

(1)

un-1(x)un+1(x)-(un(x))2=-(-q)n-1

(2)

un+r(x)un+r+h(x)-(-q)2r+hun-r(x)un-r-h(x)=

u2n(x)u2r+h(x)

(3)

证明利用Binet公式即可证得式(1)与式(3)，在式(1)中令m=n-1可得式(2)。注意式(1)为D’Ocagne恒等式的推广，式(2)为Simson恒等式的推广，且式(2)在文献[1]的定理2.21中已经给出。此外，式(3)推广了文献[7]的定理2.1。

引理1设wn(x)=un(x)un+h(x)，则序列(wn(x))满足如下递推关系：

wn(x)=(p2+q)wn-1(x)+(p2q+q2)wn-2(x)-

q3wn-3(x)，(n≥3).

证明利用序列(un(x))的递推公式，有：

wn(x)=un(x)un+h(x)=(pun-1(x)+

qun-2(x))(pun+h-1(x)+qun+h-2(x))=

p2wn-1(x)+qun+h-1(x)(un-1(x)-

qun-3(x))+pqun+h-2(x)(pun-2(x)+

qun-3(x))+q2wn-2(x)=

(p2+q)wn-1(x)+(p2q+q2)wn-2(x)-

q2un-3(x)(un+h-1(x)-pun+h-2(x))=

(p2+q)wn-1(x)+(p2q+q2)wn-2(x)-

q3wn-3(x)，

故得证。

利用引理1可进一步得到序列(wn(x))的生成函数。

引理2序列(wn(x))的生成函数为：

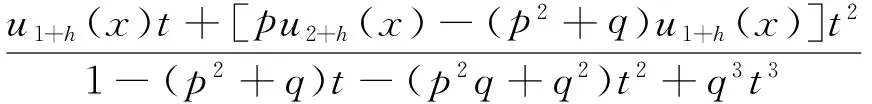
证明利用(wn(x))的递推关系，可得：

q2)wn-2(x)-q3wn-3(x)]tn=w1(x)t+

w1(x)t+w2(x)t2-(p2+q)w1(x)t2+

(p2+q)tf(x,t)+(p2q+q2)t2f(x,t)-

q3t3f(x,t)，

由上述方程解出f(x,t)即可。

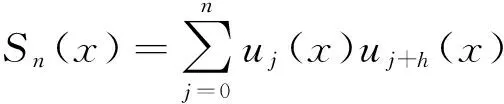
定理2序列(Sn(x))满足如下递推关系：

Sn(x)=(p2+q+1)Sn-1(x)+(p2q+q2-p2-

q)Sn-2(x)-(q3+q2+p2q)Sn-3(x)+

q3Sn-4(x)，(n≥4).

证明序列(Sn(x))的生成函数为：

由此可得：

u1+h(x)t+[pu2+h(x)-(p2+q)u1+h(x)]t2=

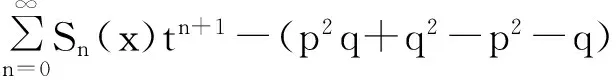
对等式两边取tn的系数，即可得证。

引理2及定理2推广了文献[7]中3.3节的结论。利用定理2及初始条件

S0(x)=0，S1(x)=u1+h(x)，

S2(x)=u1+h(x)+pu2+h(x)，

S3(x)=u1+h(x)+pu2+h(x)+(p2+q)u3+h(x)，

可以递推地计算：

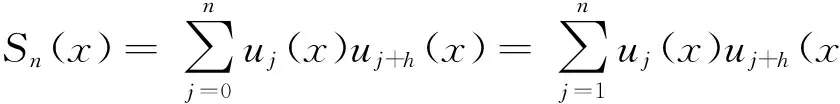
定理3设k≥l≥1, h≥i，则(p,q)型Fibonacci多项式序列(un(x))满足如下恒等式：

其中：

A(x)=vk+l+h+i(x)-v(n+1)(k+l)+h+i(x)-

(-q)k+lvh+i(x)+(-q)k+lvn(k+l)+h+i(x)，

B(x)=(-q)(n+1)l+iv(n+1)(k-l)+h-i(x)-

(-q)l+i(x)vk+h-l-i(x)+(-q)k+l+ivh-i(x)-

(-q)(n+1)l+k+ivn(k-l)+h-i(x).

证明将Binet公式代入和式并整理得：

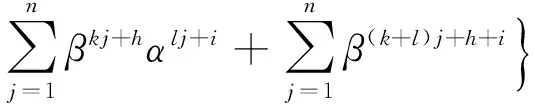
利用等比数列求和公式，并将所得结果中的第1项和第4项通分合并，第2项和第3项通分合并，利用αβ=-q以及vn(x)=αn+βn，即可得到所求结果。

推论1当k=l=1，i=0时，有：

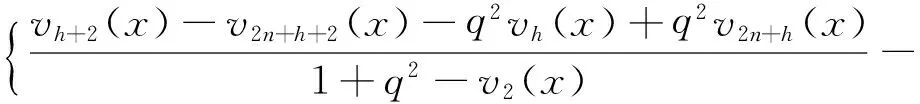
(4)

推论2当k=l≥1，h=i=0时，有：

(5)

对式(4)和(5)中的k、l、h、i取不同的值，还能得到一些特殊形式的乘积之和的封闭形式。

2　一些应用

下面将两个(p,q)型Fibonacci多项式的乘积之和的结果应用到经典的Fibonacci多项式及Chebyshev多项式上。

例1当p(x)=x, q(x)=1时，un(x)为Fibonacci多项式Fn(x), vn(x)为Lucas多项式Ln(x)，这时有：

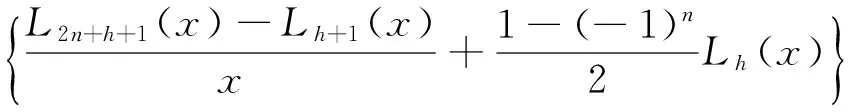
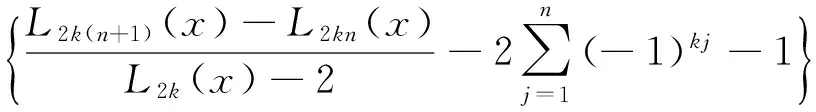
进一步，当h=0，1，2时，有：

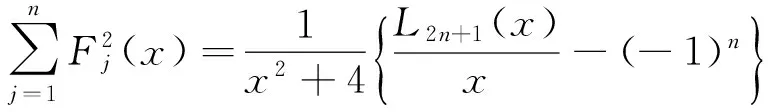
当k=2，3时，有：

例2当p(x)=2x, q(x)=-1时，un(x)为第二类Chebyshev多项式Un-1(x), vn(x)为第一类Chebyshev多项式2Tn(x)，这时有：

于是，当h=0，1，2时，有：

当k=2，3时，有：

3　结　论

本文研究了两个(p,q)型Fibonacci多项式的乘积与乘积之和的递推关系及表达式，并将其应用到经典的Fibonacci多项式以及Chebyshev多项式上。用类似的方法也可以得到其他特殊的多项式满足的递推关系与恒等式。

[1] LEE G Y, ASCI M. Some properties of the(p,q)-Fibonacci and(p,q)-Lucas polynomials[J/OL]. Journal of Applied Mathematics, 2012: 1-18. http://dx.doi.org/10.1155/2012/264842.

[2] WANG J Z. Some new results for the(p,q)-Fibonacci and Lucas polynomials[J]. Andvances in Difference Equations. 2014, 64: 1-15.

[3] HE T X, SHIUE P J S. On sequences of numbers and polynomials defined by linear recurrence relations of order 2[J/OL]. International Journal of Mathematics and Mathematical Sciences. 2009: 1-12. http://dx.doi.org/10. 1155//2009/709386.

[4] CHEON G S, KIM H, SHAPIRO L W. A generalization of Lucas polynomial sequence[J]. Discrete Applied Mathematics, 2009, 157(5): 920-927.

[5] MA S M. Identities involving generalized Fibonacci-type polynomials[J]. Applied Mathematics and Computation, 2011, 217(22): 9297-9301.

[6] NALLI A, HAUKKANEN P. On generalized Fibonacci and Lucas polynomials[J]. Chaos Solitons Fractals, 2009, 42(5): 3179-3186.

[7] FALCON S. On the sequences of products of twok-Fibonacci numbers[J]. American Review of Mathematics and Statistics, 2014, 1(2): 111-120.

(责任编辑： 康锋)

Studies on Products of Two (p,q)-Fibonacci Polynomials

WANGHui,WANGWeiping

(School of Science, Zhejiang Sci-Tech University, Hangzhou 310018, China)

By combinatorial method, the identities, recurrence relation and generating function of the products of two (p,q)-Fibonacci polynomials are studied, and the recurrence relation and explicit expressions of the sums of such products are established. These results generalize those of Faclon. Moreover, many new combinatorial identities are established by applying the general results on the sequence of (p,q)-Fibonacci polynomials to the classical Fibonacci polynomials and Chebyshev polynomials.

(p,q)-Fibonacci polynomials; (p,q)-Lucas polynomials; generating functions; recurrence relations; combinatorial identities

10.3969/j.issn.1673-3851.2016.01.025

2015-04-03

浙江省自然科学基金项目(ZY13A010016)

王慧(1988-)，女，湖北黄梅人，硕士研究生，主要从事组合数学方面的研究。

王伟平，E-mail：wpingwang@zstu.edu.cn

O157.1

A

1673- 3851 (2016) 01- 0145- 05 引用页码： 010804