非线性薛定谔方程的非局域对称

杜晓阳，费金喜，马正义

(1.浙江理工大学理学院，杭州 310018；2.丽水学院工程与设计学院，浙江丽水 323000)



非线性薛定谔方程的非局域对称

杜晓阳1，费金喜2，马正义2

(1.浙江理工大学理学院，杭州 310018；2.丽水学院工程与设计学院，浙江丽水 323000)

基于非线性薛定谔方程及其Lax对，通过恰当的对称假设，得到了薛定谔方程含Lie点对称的非局域对称。由于所得到的非局域对称不能直接用来构造方程的精确解，为此引入了一个辅助变量，将薛定谔方程的非局域对称局域化为拥有扩大空间的Lie点对称，从而构建了封闭的延拓系统。在对称约化过程中，得到了与雅可比函数相关的显式解，其图像显示了孤波和椭圆余弦波之间的相互作用。

薛定谔方程；非局域对称；Lax对；延拓系统；精确解

0　引　言

非线性偏微分方程(nonlinear partial differential equation，NPDE)，是现代数学的一个重要分支。它常常被用来描述力学、控制系统、化工循环系统、流行病等领域的问题，对这些现象的研究最终可归结为微分方程的求解问题。然而，由于结构的复杂性，大部分NPDE的解是无法用现有的方法直接得到的，有的也仅是近似解。另外，随着人们对其研究的深入，有些原先可用线性微分方程近似处理的问题，如今也必须考虑非线性对其造成的影响。因此，对NPDE的研究，尤其是对其如何求精确解，就具有很重要的意义。

正是因为这样，众多学者在如何求解NPDE方面做了很多研究，提出了很多研究方法，如反散射法、Hirota双线性法、Painlevé有限展开法、Bäcklund变换法、Darboux变换法，Lie群法等。就Lie群法而言，自从Sophus Lie的Lie群理论被引入，它就被广泛用于寻找偏微分方程的Lie点对称。关于Lie群和Lie对称问题的研究，我国学者在约束力学系统微分方程的Lie对称性和守恒量方面做出了很大的贡献。如，赵跃宇和梅凤祥[1-2]首次利用Lie群理论研究了非保守约束力学系统的对称性与守恒量问题，这对我国分析力学的发展起了很大的推动作用。近几年来，学者傅景礼、周莎、高芳等讨论了分数阶Hamiltonian系统的对称理论和用正则坐标解决单自由度的约束机制系统[3-4]。另一方面，Bluman等[5-6]在Lie群基础上提出了非经典的Lie群法，即条件对称。Fokas等[7]、Zhdanov[8]提出了条件Lie Bäcklund对称法，并将其进行了完善。然而，在一般情况下，通过Lie点对称和Lie Bäcklund对称得到的非局域对称有可能会丢失一些重要的项，如更高阶的导数项等。Lou等[9-10]通过对KdV方程的非局域对称进行局域化，得到了在孤波和椭圆余弦波之间相互作用的新的精确解，从而使该问题得到了解决。随后，Xin等[11-12]使用该方法先后得到了AKNS系统和Boussinesq方程的与实际紧密联系的新的精确解，再一次证实了该方法的有效性。

研究非线性薛定谔方程非局域对称局域化，是因为非线性系统的非局域对称可以扩大对称的类，从而可以求到方程新的精确解。对非线性系统而言，方程的精确解不仅对于相关学科及其现象的研究有至关重要的作用，而且可以提供控制数值的精确信息，从而有助于发现一些新的自然现象。众所周知，非线性薛定谔方程是由奥地利物理学家薛定谔在1926年提出的一个用于描述波函数的运动方程，被认为是量子力学的奠基理论之一。本文通过求解该方程的非局域对称，构造了它的新的精确解。

1　薛定谔方程的非局域对称

非线性薛定谔方程的一般形式为[13]：

(1)

(2)

它们满足兼容条件ψxt=ψtx和φxt=φtx。其中 u,v是关于x,t的波函数。

本文提供了一种寻找薛定谔方程的非局域对称的方法。该方法不同于传统方法的地方在于，使用它不仅可以得到所求方程的非局域对称，而且还可以得到其传统对称。具体方法如下：

首先，把薛定谔方程的对称σ1,σ2定义成它的线性方程的解的形式，可表示为：

(3)这就意味着薛定谔方程在无穷小变量ε的变换u→u+εσ1，v→v+εσ2下形式不变，在这里，σ1，σ2是对称元。

然后，假设对称σ1,σ2有如下形式：

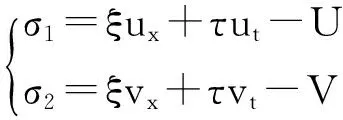
把上式代入方程(3),在计算的过程中分别代入方程(1)和(2)，通过消除ψx、ψt、φx、φt，可以得到关于ξ、τ、U、V的决定性方程。它们的解分别是：

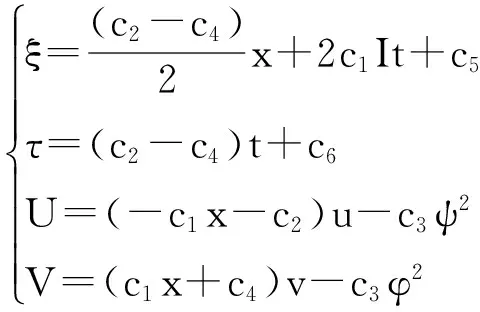
其中ci(i=1，2，…，6)为任意常数。这些计算可借助于软件Maple完成。

因此，方程(1)的对称可表示为：

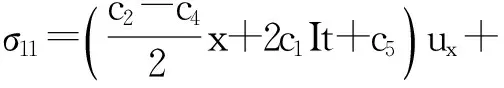
在方程(4)中令c1=c2=c4=c5=c6=0，c3=1，则方程(1)的对称被简化为：

(5)

通过对薛定谔方程的Lax对的观察可以发现，在Lax对中最高阶导数项为ψx、φx、ψt、φt，它们皆是一阶导数，所以在对称σ1,σ2中ψ,φ的阶数肯定不超过1。因此，如果假设函数U,V含有变量的话，则可能会得到薛定谔方程的更为一般的解。

2　非局域对称的局域化

众所周知，微分方程的非局域对称不能直接用来构造方程的精确解，因此需要把非局域对称转化成局域对称，即非局域对称局域化。

从方程(5)中可以看出，薛定谔方程的非局域对称中含有ψ和φ，为了把它们局域化，首先需要求解Lax方程组(2)的线性形式的解：

(6)

其中ψ→ψ+εσ3，φ→φ+εσ4。

然后，联立方程(5)和(6)得：

(7)

其中新变量p的定义为：

px=ψφ

(8)

并且p满足：

pt-uφ2I-4λψφ+ψ2vI=0

(9)

由于新变量p的出现，接下来同样需要求解方程(8)和(9)的线性解，即：

(10)

在方程(10)中p→p+εσ5。最后，将方程(10)代入方程(9)中，可得：

σ5=p2

(11)

从(7)和(11)中可以看出，薛定谔方程(1)的非局域对称已由原来的空间{x,t,u,v} 的非局域对称成功地转化成一个扩大空间{x,t,u,v,ψ,φ,p} 的局域对称，且该空间的向量形式为：

V1=ψ2∂u+φ2∂v+ψp∂ψ+φp∂φ+p2∂p

(12)

通过Lie点对称(12)，求解以下初始问题：

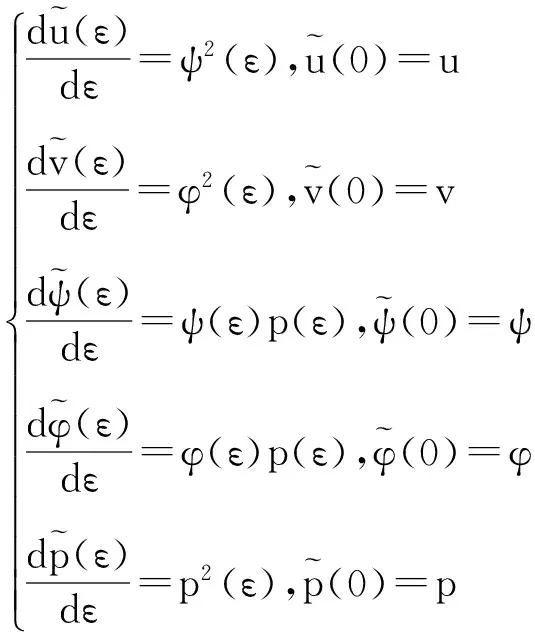
从而得到的有限的对称变换为：

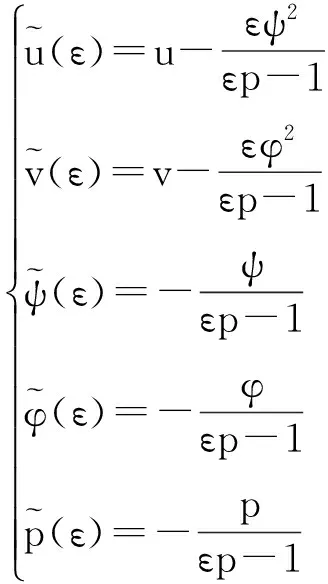
说明：从上述方程中可以看出，给定方程(1)的一个解，就可以通过以上的对称变换得到它的另一个解。其中{u,v,ψ,φ,p)是方程(1)、(2)和(8)构成的延拓系统的解，且该延拓系统是封闭的。

为了得到更多方程(1)的相似解，假设Lie点对称的延拓系统有形式：

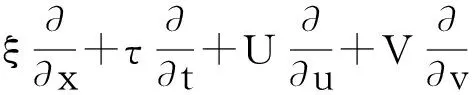
(13)

在变换

{x→x+εξ, t→t+ετ,u→u+εU,v→v+εV,ψ→ψ+εΨ,φ→φ+εΦ,p→p+εP}下，方程(13)也可以写成如下形式：

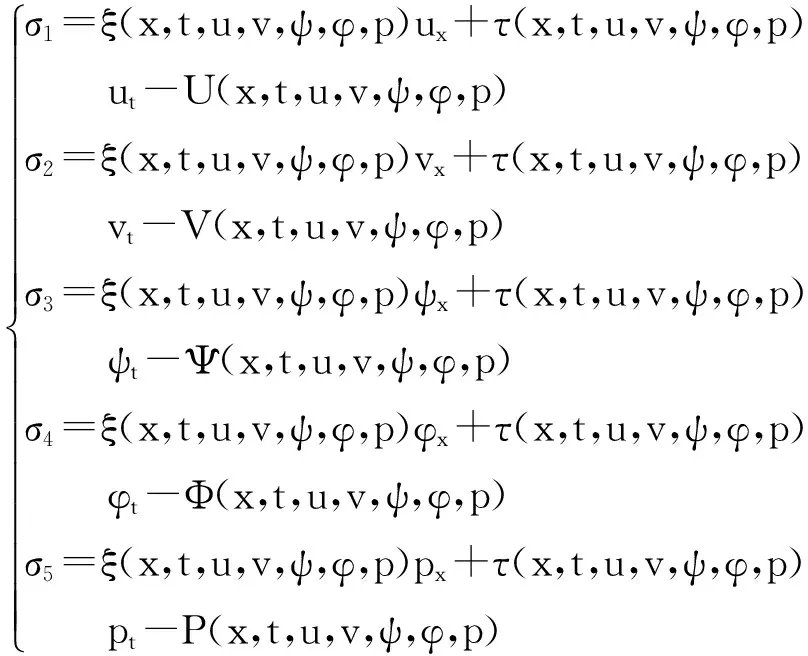
然后将上式代入延拓系统中，经过计算可得：

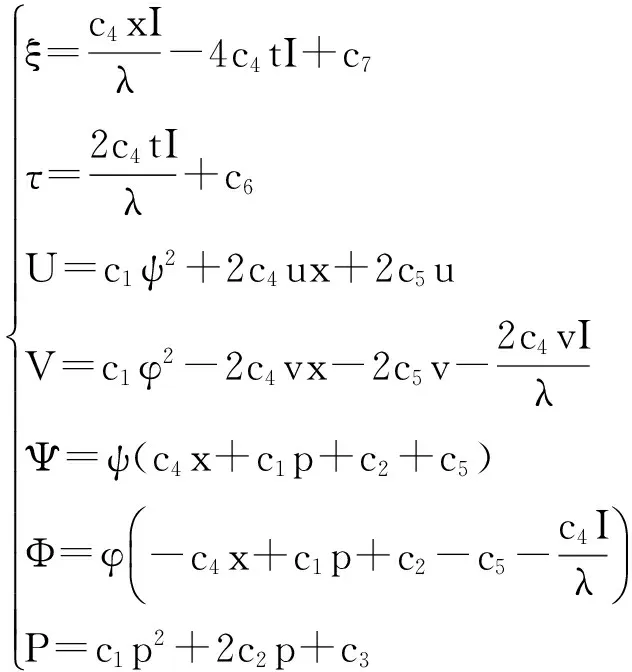
3　薛定谔方程的对称约化

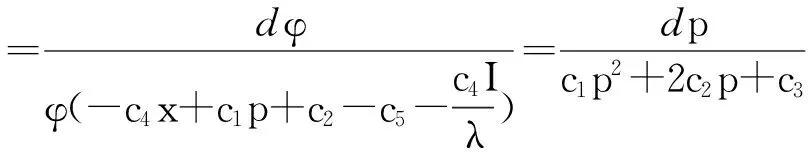
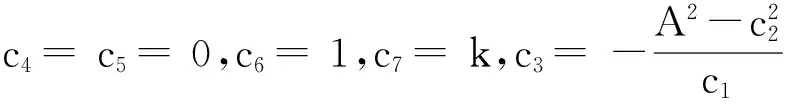
(14)

其中：X=x-kt，P(X),Q(X),Q1(X),U(X)和V(X)分别代表群不变量。将方程(14)代入延拓系统后，可发现它们之间是相互兼容的，且满足式(15)：

(15)

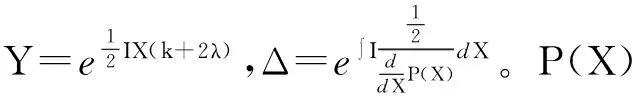
(16)

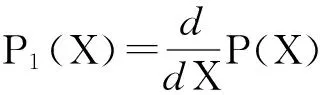
由于上述ODE的解可以写成雅可比椭圆函数的形式，故在这里本文给出该方程的一个雅可比解P1(X)=a1+a2JacobiSN(a3X,m)，以此解为前提，将其代入方程(14)，(15)和(16)中，经过计算，可以得到薛定谔方程新的显式解，且它的参数满足：

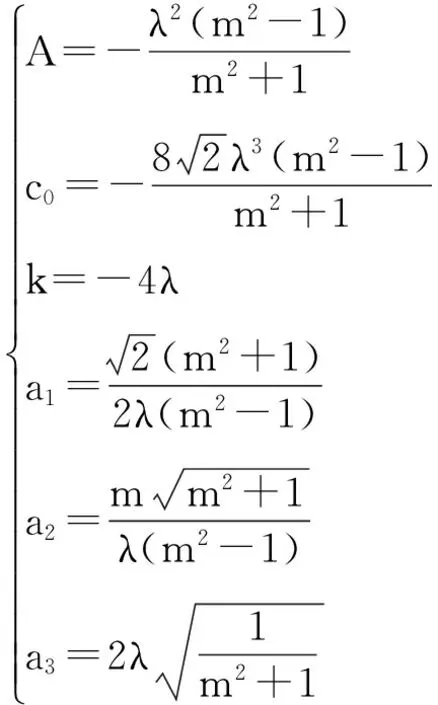
图时的解的结构

图1显示的是非线性薛定谔方程在椭圆周期波背景下一个孤波的传播结构。图1(a)展示的是解u在时空状态下孤波的传播，图1(b)-(d)表示解u在不同的时间(分别为t=-5,0,5)孤波在周期波背景下的演化。从结构上看，随着时间的增加，孤子从右往左移动，但高度不变。自然界中，该现象可以在海平面上观察到，对船舶安全和海岸工程具有重要影响。

4　结　论

本文以Lie点对称为基础，通过对称假设得到了非线性薛定谔方程的非局域对称。随后，引入了辅助变量px=ψφ，并借助于它将非局域对称局域为拥有封闭延拓系统的Lie点对称。然后对得到的Lie点对称进行对称约化，最后得到了非线性薛定谔方程的新的精确解。

然而，该方法也有一定的不足。没有统一的方法判断一个NPDE是否可用此方法求解，且寻找适当的辅助变量并不是一件易事，它需要一定的技巧和繁琐的计算过程。

[1] 赵跃宇，梅凤祥. 力学系统的不变量与对称性[M]. 科学出版社，1999.

[2] 梅凤祥. 李群和李代数对约束力学系统的应用[M]. 科学出版社，1999.

[3] GAO F, ZHANG X B, FU J L. Application of canonical coordinates for solving single-freedom constraint mechanical systems[J]. Applied Mathematics and Mechanics, 2014, 35(8): 1029-1038.

[4] ZHOU S, FU H, FU J L. Symmetry theories of Hamiltonian systems with fractional derivatives[J]. Science China: Physics, Mechanics & Astronomy, 2011, 54 (10): 1847- 1853.

[5] BLUMAN G W，COLE J D．The general similarity solution of the heat equation[J]. Math Mech, 1969, 18：1025-1042．

[6] BLUMAN G W, COLE J D. Similarity Method for Differential Equation[M]. Springer-Verlag, New York, 1974: 33-97.

[7] FOKAS A S, LIU Q M. Nonlinear interaction of traveling waves of nonintegrable equations[J]. Physical Review Letters, 1994, 72(21): 3293-3296.

[8] ZHDANOV R Z. Conditional Lie-Backlund symmetry and reduction of evolution equations[J]. Journal of Physics A: Mathematical and General, 1995, 28(13): 3841-3850.

[9] LOU S Y. Conformal invariance and integrable models[J]. Journal of Physics A: Mathematical and General, 1997, 30(13): 4803-4813.

[10] LOU S Y, HU X B. Non-local symmetries via Darboux transformations[J]. Journal of Physics A: Mathematical and General, 1997, 30(5): L95-L100.

[11] MIAO Q, XIN X, CHEN Y. Nonlocal symmetries and explicit solutions of the AKNS system[J]. Applied Mathematics Letters, 2014, 28: 7-13.

[12] XIN X, CHEN J, CHEN Y. Nonlocal symmetries and explicit solutions of the Boussinesq equation[J]. Chinese Annals of Mathematics: Series B, 2014, 35(6): 841-856.

[13] ABLOWITZ M J, KAUP D J, NEWELLl A C, et al. Method for solving the sine-Gordon equation[J]. Physical Review Letters, 1973, 30(25): 1262.

(责任编辑： 康锋)

Nonlocal Symmetry of Nonlinear Schrödinger Equation

DUXiaoyang1,FEIJinxi2,MAZhengyi2

(1.School of Science, Zhejiang Sci-Tech University, Hangzhou 310018, China; 2.Institute of Engineering and Design, Zhejiang Lishui University, Lishui 323000, China)

Based on the nonlinear Schrödinger equation and its Lax pair, we obtained the nonlocal symmetry of Schrödinger equation containing Lie point symmetry through appropriate symmetry hypothesis. Since the nonlocal symmetry cannot be directly used to construct exact solutions of the equation, an auxiliary variable was introduced. With the introduction of it, the nonlocal symmetry was localized to Lie point symmetry which has expanded space. And based on it, a closed prolonged system was established. The explicit solution related to Jacobi function was obtained in symmetry reduction process. The image shows some interactions between cnoidal wave and solitary wave.

Schrödinger equation; nonlocal symmetry; Lax pair; prolonged system; exact solution

10.3969/j.issn.1673-3851.2016.01.024

2015-04-22

国家自然科学基金项目(11447017); 浙江省自然科学基金项目(LY14A010005)

杜晓阳(1990-)，女，山西长治人，硕士研究生，主要从事非线性数学物理方程的研究。

马正义，E-mail: ma-zhengyi@163.com

O175.29

A

1673- 3851 (2016) 01- 0140- 05 引用页码： 010803