基于模糊神经网络PID的永磁同步直线电机控制算法研究
党明辉,郭 亮
(浙江理工大学机械与自动控制学院,杭州 310018)
基于模糊神经网络PID的永磁同步直线电机控制算法研究
党明辉,郭亮
(浙江理工大学机械与自动控制学院,杭州 310018)
针对永磁同步直线电机(PMLSM)系统模型参数的时变性、非线性以及负载扰动等问题,在建立永磁同步直线电机的动态数学模型的基础上,结合传统PID算法和具有强自适应能力、强抗干扰能力的模糊神经网络智能算法的优点,提出一种基于模糊神经网络PID的永磁同步直线电机控制算法。运动控制系统仿真实验结果表明:系统经模糊神经网络PID控制静态误差为零、干扰影响小,过渡过程时间缩短近50%,相对于传统PID控制和模糊PID控制具有更高的控制精度、更好的动态特性和静态特性。
永磁同步直线电机; PID控制; 模糊神经网络
0 引 言
永磁同步直线电机(PMLSM)组成的直线伺服系统,由于取消了从旋转电机到工作台间的所有机械传动环节,极大地提高了进给系统的快速反应能力和运动精度,具有高速、高精和直接驱动的特性,近年来在加工中心、数控铣床、车床等高档数控机床中得到了广泛应用。但直接驱动方式也同时使得永磁同步直线电机和工作台之间没有了缓冲环节,负载变化、参数摄动等因素直接作用于直线电机,系统控制难度增加,直线电机铁心饱和引起的非线性和强耦合性等特征,也进一步增加了电机控制系统的难度[1-4]。
传统PID控制器(proportion integration differentiation,比例-积分-微分控制器)具有原理简单、使用方便、稳定性好、鲁棒性强等特点,在实际工业领域有着很广泛的应用。但它对数学模型的依赖性强、参数确定后无法更改,这个特性使其无法满足非线性永磁同步直线电机的控制要求。许多专家学者结合传统PID控制和鲁棒控制、模糊控制、神经网络控制、滑膜变结构控制等控制方法的优点,提出了鲁棒PID控制、模糊PID控制、神经网络PID控制、变结构PID控制等控制方法[5-7]。鲁棒PID控制是基于最小-最大原理,针对系统最恶劣运行状况进行设计,虽控制效果较好,但随着控制系统阶次的增加,计算量急剧增大,增加了系统的复杂程度。模糊PID控制通过模糊算法实现了PID参数自适应调节,但其模糊规则和隶属度函数的确定仍需通过经验来选择。神经网络PID控制系统中也同样存在隐含层数目和初始权值难以确定的问题[8-9]。
本文结合了模糊控制、神经网络控制、PID的特点,提出了一种基于模糊神经网络PID的永磁同步直线电机控制控制算法。该算法利用模糊神经网络结构通过学习训练系统输入输出对PID参数进行调整,在实现系统稳定控制的同时,具有参数辨识、自学习、自适应的特点,不仅可以满足了具有负载绕组的非线性永磁同步直线电机控制系统需求,且与其他方法相比更适合应用于对伺服性能要求较高的直线电机控制系统。
1 永磁同步直线电机的工作原理
本文研究对象为动初极型永磁同步直线电机,其结构原理如图1所示。其中:1为定子,表面均匀开槽并放置三相绕组;2为动子,铁心表面粘贴有垂直充磁的永磁体,以形成励磁磁场。当定子绕组通有三相交流电时,在磁场的作用下可产生的电磁力驱动动子沿直线导轨做往复运动。为方便电磁力求解,工程上通常使用坐标变换将相对励磁磁场运动的ABC坐标系转化为相对励磁磁场静止的d-q轴坐标系,坐标系如图2所示。

1:定子;2:动子;3:行波磁场;4:N、S永磁体;5:间隙vs行波磁场移动速度;vr:动子移动速度图1 永磁同步直线电机结构原理

图2 ABC坐标系和d-q轴坐标系
根据永磁电机特点,假设:a)永磁体初级为无阻尼绕组;b)忽略温度对电机参数的影响;c)忽略磁滞损耗及涡流损耗的影响;d)忽略反电动势谐波影响。那么ABC坐标系到d-q坐标系的转换矩阵可由式(1)[6-8]:
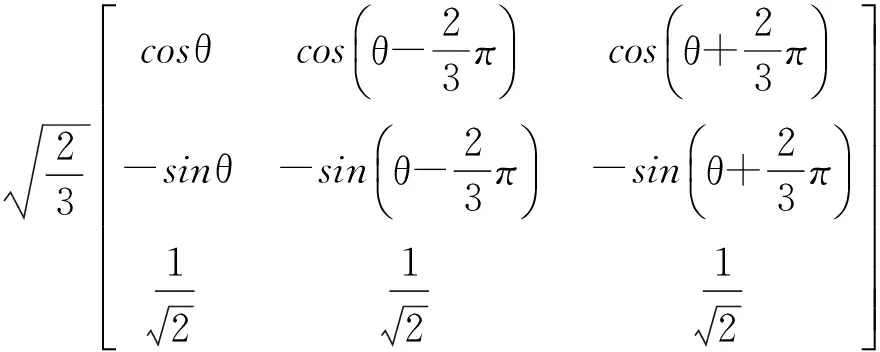
(1)
(2)
(3)
(4)
其中:ud、uq、id、iq分别为d轴和q轴的电压和电流,Ld、Lq分别d轴和q轴电感系数,Ψf是定子永磁体磁链,R是各相绕组线圈的电阻,f是直线电机的频率,Np是电机的极对数,τ是极距。对于Ld=Lq的隐极式电机,当采用id=0控制策略时,电磁推力可简化为:
(5)
永磁同步直线电机机械运动方程可由式(6)表示:
(6)
其中:M为直线电机的质量,Fd为直线电机的负载阻力,Bv为黏滞摩擦系数。
2 基于模糊神经网络PID控制器
2.1永磁同步直线电机控制系统结构
本文建立的永磁同步直线电机的控制系统基本结构如图3所示。该系统主要包括:电流环和速度环。电流环包括id=0控制器和iq控制器,采用传统的PID控制器实现内环电流控制。速度环实现外环速度控制,控制结果作为电流环的输入,其控制效果的好坏将直接影响电流环进而影响系统整体性能,因此速度调节算法选用合适的控制策略非常重要。

图3 永磁同步直线电机控制系统框图
本文在速度环中引入模糊神经网络算法,将传统PID算法和模糊神经网络控制相结合,设计了模糊神经网络PID速度控制器。模糊神经网络PID结构如图4所示,速度比较产生的误差e和误差变化率ec作为模糊神经网络组成的PID参数调节器的输入,在模糊神经网络内部经过比例因子调整后得E和EC,经学习训练过的模糊神经网络输出P、I、D经过比例因子调整后得到最佳的比例常数kp、积分常数ki和微分常数kd输入PID控制器。
背诵绝不是早读课的专利。相反,只把背诵任务留给早读,往往在任务驱动中让背诵成为死记硬背,如果不能及时复习巩固,“艾宾浩斯曲线”告诉我们,背诵内容很快就会烟消云散。越来越多的语文老师重视课堂渗透和指导,将背诵融入课堂教学的一部分。一位教师在教学《绝句(两个黄鹂鸣翠柳)》中,在多种形式感悟情境、朗读诗句的基础上,出示引导背诵PPT:

图4 模糊神经网络PID控制框图
模糊神经网络模型输入层、隶属度函数生成层、模糊推理层、归一化层和精确化层,其模型如图5所示。a)隶属度函数生成层:该层共两个输入,每个输入有7个节点,分用字母PB、PM、PS、ZO、NS、NM、NB表示。对输入进行模糊化的隶属度函数如式(7)所示的高斯函数:
(7)
其中:i=1, 2;j=1,2,3,4,5,6,7;cij和bij分别表示第i个输入变量和第j模糊集合的隶属度的中心和宽度。b)模糊推理层:共7个节点,同模糊化层7个节点相连完成模糊规则匹配。模糊推理层一个节点的输出是所有该点输入信号的乘积。c)归一化层:对模糊推理层的结果进行归一化运算。d)精确化层:实现对结果的计算,其连接权值为ωij。模糊神经网络学习的参数主要是连接权值ωij和隶属度函数的中心值cij和宽度值bij,学习方法采用BP神经网络学习法。在单输出情况下,定义误差函数可由式(8)表示:

图5 模糊神经网络模型
(8)

为了让实际输出最大程度上逼近理想输出,E(k)需达到最小,本文采用最速下降法进行搜索,搜索算法可由式(9)表示:
(9)
其中:Θ=(cij,bij,wij),cij为隶属度函数生成层隶属度函数中心值,bij为隶属度函数生成层隶属度函数宽度值,wij为归一化层与精确化的连接权值。通过神经网络最速寻优法得到的三参数表达式为:
(10)
其中:η为学习速率,α为动量因子。
2.2模糊神经网络的训练
通过Matlab中的anfisedit工具箱对神经网络进行训练。对设计好的模糊PID仿真系统的输入输出进行采集作为训练样本,采用BP神经网络误差逆向传播学习算法对该系统进行训练,设置误差允许值为0,训练次数为600次,误差曲线如6所示。
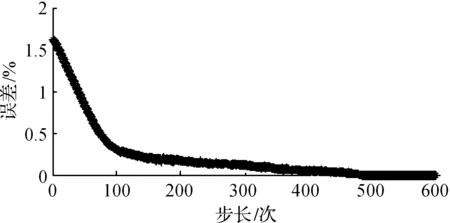
图6 训练后误差曲线
训练前后的E和EC的隶属度函数对比如图7所示。由图7可知:当系统误差E大小在NM、ZO、PS顶点值附近时,系统比较稳定,此时分辨率是系统主要考虑因素,所以隶属度函数都变得十分陡峭;当系统误差E大小在除了NM、ZO、PS顶点值附近以外的区域时,系统分辨率较高,此时稳定性是系统主要考虑因素,所以隶属度函数变得很平缓;当系统误差变化率EC大小在NM、NS、PS、PM顶点值附近时,系统比较稳定,此时分辨率是系统主要考虑因素,因此隶属度函数此时坡度较大;当系统误差变化率EC大小在NB、ZO、PB附近区域时,系统分辨率较高,此时稳定性是系统主要考虑因素,所以隶属度
函数曲线变得很平缓。训练后的隶属度函数更加符合实际情况。
训练前后P、I、D输出曲面如图8所示。从图8中可以发现,训练后P、I、D输出曲面变得更加平滑,说明控制更加平稳。

图7 训练前后E和EC隶属度函数

图8 训练前后P、I、D输出曲面
3 系统仿真与实验
3.1系统仿真
根据实验室样机模型,取永磁同步直线电机参数为Rs=3.16Ω,Ld=Lq=30.12Mh,M=4kg,τ=30mm,BV=4N·s/m,Ψf=0.3V·s时,基于模糊神经网络PID速度控制器的永磁同步直线电机整体仿真框图如图9所示。由图9可以看出在该控制系统中,以永磁同步直线电机为控制对象,电流环采用传统的PID控制器,速度环采用本文所设计速度控制器。

图9 直线电机控制系统整体仿真模型
图10为给定永磁同步直线电机控制系统一个速度为4mm/s阶跃信号时,分别采用传统PID控制、模糊PID控制和模糊神经网络PID控制策略下的系统输出曲线。通过比较可以看出,与传统PID和模糊PID控制策略相比,模糊神经网络PID的控制方法稳态误差更小,调整时间更短,系统响应速度更高,其各项指标参数如表1所示。在t=0.075s时刻,给系统一个100N的负载干扰信号,分别采用上述3种控制方法的输出曲线如图10中的后半段所示,其放大图如图10中箭头所指。由图10可知,模糊神经网络PID控制系统受负载干扰的影响更小,该系统相对于传统PID和模糊PID控制下的系统鲁棒性更强。

图10 不同控制系统下干扰响应对比曲线

控制算法超调量σp/%上升时间tr/s调整时间ts/s稳态误差ess/%PID14.30.17400.41300.76模糊PID2.70.01670.03310.06模糊神经网络PID00.01600.02430
3.2实验验证
为了验证模糊神经网络PID控制效果,本文搭建了基于TMS320F2812DSP的永磁直线电机控制平台,分别使用PID控制策略和模糊神经网络PID控制策略对直线电机进行了阶跃响应实验。实验整体系统如图11所示。

图11 直线电机系统实验平台
在此闭环控制系统中,控制器首先接收来至光栅的速度信号和来之电流传感器的电流信号,经过算法程序处理后输出PWM波形信号给驱动器,在驱动器中信号经光耦隔离后驱动逆变器产生三相电流给电机供电,此时电流传感器和光栅再次采集相应的信号输出给控制器完成一次循环,经过多次循环控制电机达到需求状态。给定直线电机一个7mm/s的速度信号,采用传统PID控制和模糊神经网络PID控制下的速度输出曲线如图12和图13所示。由图12可以看出,传统PID控制下的速度响应曲线输出超调较大,调整时间较长,模糊神经网络PID控制下的速度响应超调较小,调整时间较短,实验结果和仿真结果相吻合,进一步说明基于速度环模糊神经网络PID控制能明显提高直线电机伺服系统的动态特性和静态特性。

图12 传统PID控制下的速度响应

图13 模糊神经网络PID控制下的速度响应
4 结 语
本文针对永磁同步直线电机系统模型不确定性和负载扰动性的特点,设计了一种模糊神经网络
PID控制器,并应用于三相永磁同步直线电机速度环控制,Simulink仿真和样机实验结果表明:模糊神经网络PID控制策略与传统PID和模糊PID相比,具有超调小,快速性好及运行稳定的优点,其控制效果得到了明显的提升。
[1] 吴红星, 钱海荣, 刘莹, 等. 永磁同步直线电机控制技术综述[J].微电机, 2011,44(7):76-80.
[2] 丁文双, 胡育文,鲁文其,等. 永磁同步电机模糊PID参数自整定[J]. 微特电机, 2011, 39(5): 17-21.
[3] 章达众, 廖有用, 李国平. 直线电机的发展及其磁阻力优化综述[J].机电工程.2013,30(9):1051-1054.
[5] 金朝红, 李槐树, 宋立. 基于复合控制的圆筒形永磁直线同步电机位置控制[J].电气传动,2012,42(1) : 44-48.
[6] 谢潜伟, 刘军. 永磁同步直线电机的变论域模糊PID控制[J].微电机,2013, 46(12):75-77.
[7] 方斯深, 周波, 黄佳佳, 等. 滑模控制永磁同步电动机调速系统[J]. 电工技术学报, 2008, 23(8): 29-34.
[8] 童菲, 窕勤, 袁铁江, 等. 基于神经网络的双馈风电机组转速PID控制仿真[J]. 电力系统保护与控制, 2009, 3(19):14-18.
[9] ÖZTÜRK N, ÇELIK E. Speed control of permanent magnet synchronous motors using fuzzy controller based on genetic algorithms[J]. International Journal of Electrical Power & Energy Systems, 2012, 43(1): 889-898.
(责任编辑: 康锋)
Research on PID PMLSM Control Algorithm Based on Fuzzy Neural Network
DANGMinghui,GUOLiang
(Faculty of Mechanical Engineering and Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)
According to time-varying nature, the nonlinearity, and load disturbance of permanent magnet linear synchronous motor (PMLSM) system model parameters, this paper combines traditional PID algorithm and fuzzy neural network intelligent algorithm with strong anti-interference ability and adaptive ability to propose PID PMLSM control based on fuzzy neural network on the basis of establishing dynamic mathematical model of PMLSM. Simulation experiment results of motion control system show that the motion control system based on fuzzy neural network PID control has no static error and small disturbing influence, transient time is shortened for nearly 50%. Compared with traditional PID control and fuzzy PID control, it has higher control precision, better dynamic properties and static property.
permanent magnet linear synchronous motor (PMLSM); PID control; fuzzy neural network
10.3969/j.issn.1673-3851.2016.01.009
2015-03-25
浙江省自然科学基金项目(LY14E070008)
党明辉(1989-),男,山东菏泽人,硕士研究生,主要从事直线伺服控制方面的研究。
郭亮,E-mail: lguo@zstu.edu.cn
TP173.3
A
1673- 3851 (2016) 01- 0052- 06 引用页码: 010501

