一个Hilbert型积分不等式的推广

有名辉

(浙江机电职业技术学院数学教研室，杭州 310053)



一个Hilbert型积分不等式的推广

有名辉

(浙江机电职业技术学院数学教研室，杭州 310053)

通过引进参数，借助实分析的技巧，建立了一个新的具有最佳常数因子的Hilbert型积分不等式，并考虑其等价形式，推广了相关文献的结果。

Hilbert型不等式；等价形式；Hölder不等式；Riemann Zeta 函数；Gamma函数

0　引　言

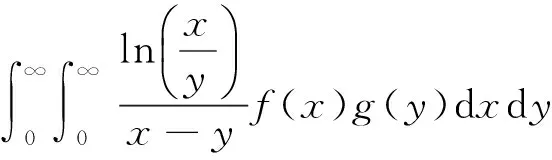
(1)

其中π2是满足(1)式的最佳常数因子[1]。不等式(1)通常被称为Hilbert型不等式。Hilbert型不等式在分析学领域有着重要的作用[2]。近来，通过引进参数，研究者们给出了式(1)及其对应的级数形式的一些推广和改进，建立了一些深刻且有价值的成果[3-8]。最近，和炳[9]又证明了一个类似于(1)式的零齐次核Hilbert型不等式，即：

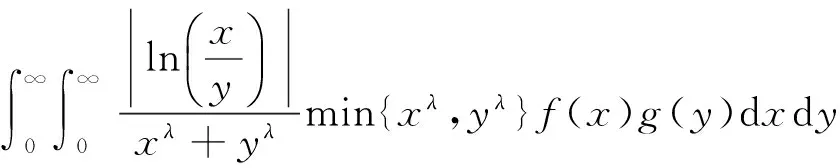
(2)

本文研究的目的是建立式(2)的推广形式。首先给出以下一些定义及引理。

定义1[10]对于a>0，定义

为第二型欧拉积分，即Γ函数。特别地，当a∈Z+时，Γ(a)=(a-1)!。

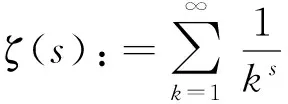
为行文方便，作以下约定：

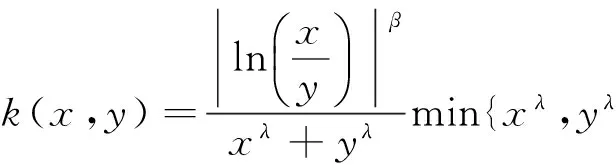
1　主要结果

引理1设λ>0,β≥0,则：

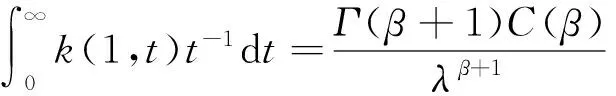
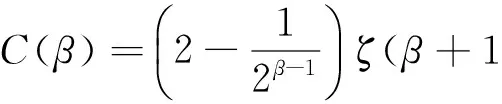
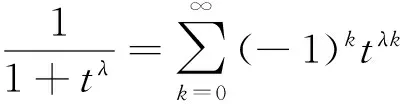
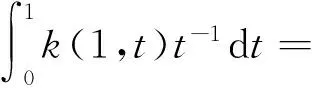
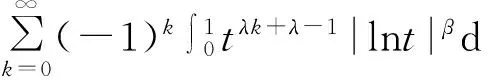
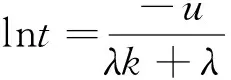
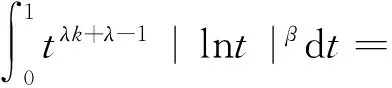
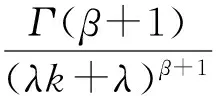
因此，

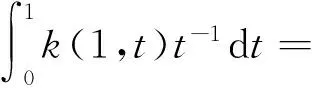
(3)

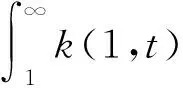
(4)

结合式(3)和式(4)，可得：

(5)

若β=0，显然有：

(6)

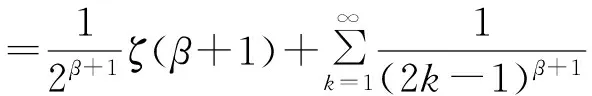
故有：

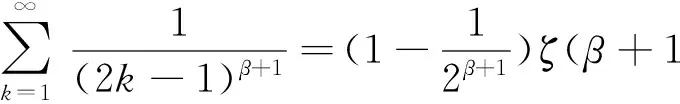
因此，当β>0时，有：

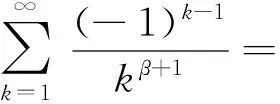
(7)

结合式(5)—(7)，即得引理1。

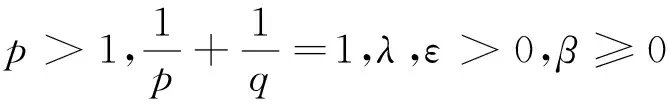
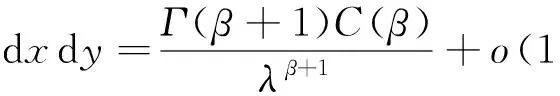
证明作变量替换y=ux，由Fubini定理，可知：

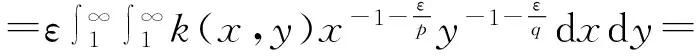
(8)

令ε→0+，由引理1，可得：

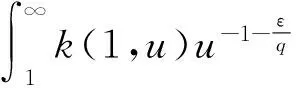
(9)

由式(8)和式(9)，即得引理2。

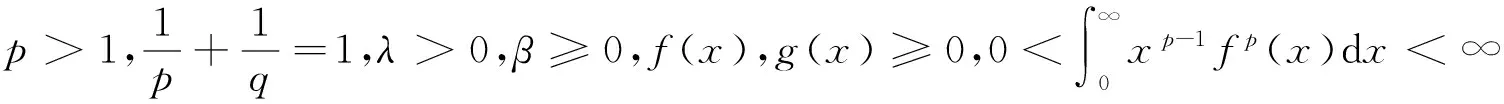
(10)

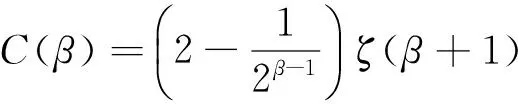
证明由Hölder不等式，可知：

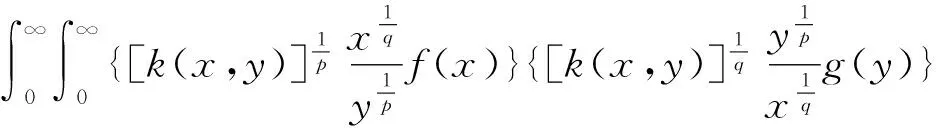
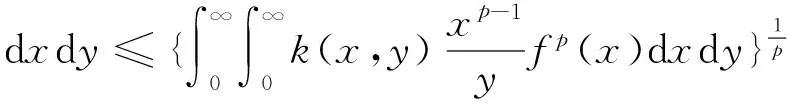
(11)

若式(11)取等号，则有不全为零的实数A与B,使得：

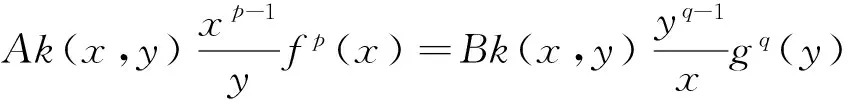
a.e.于(0,∞)×(0,∞)(参见[11])，即Axpfp(x)=Byqgq(y)a.e.于(0,∞)×(0,∞)。

于是，有常数C，使得：

Axpfp(x)=C,a.e.于(0,∞)；

Byqgq(y)=C,a.e.于(0,∞).

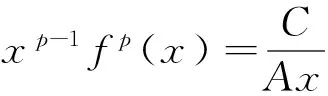
通过变量替换，根据引理1,不难算得：

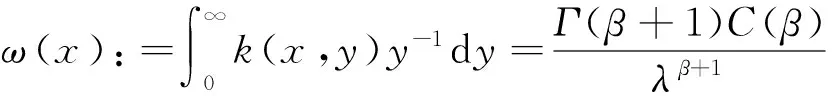
类似地，可算得：

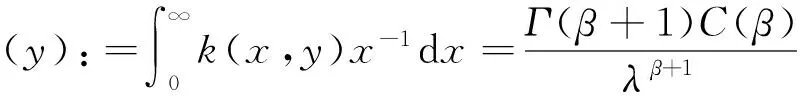
因此式(11)可写成:

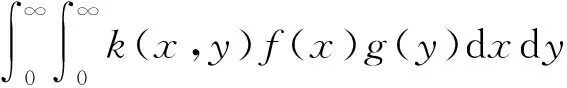
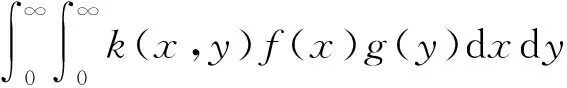
(12)

定义函数fε(x)和gε(x)(其中ε充分小)如下：

若x∈(0,1)，令

fε(x)=gε(x)=0；

若x∈[1,∞)，令

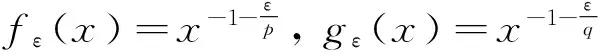
用fε和gε分别取代式(12)中的f和g，则：

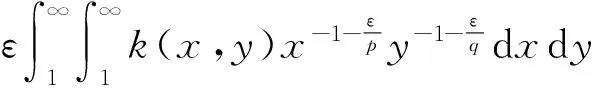
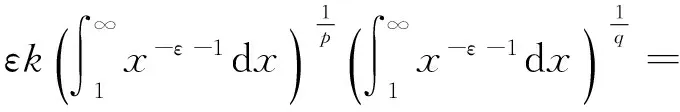
把引理2的结果代入，可得：

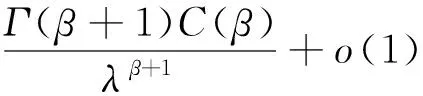
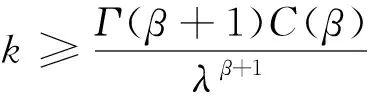
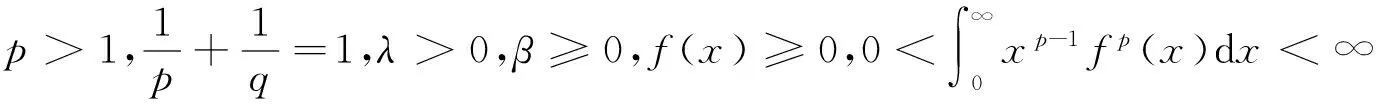
(13)

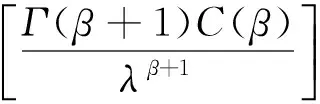
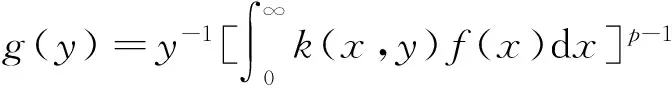
(14)

故：

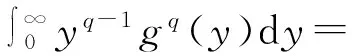
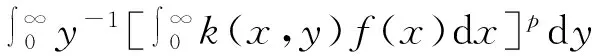
(15)

结合定理2 的条件和式(15)可知应用定理1的条件是充分的。因此式(14)和式(15)都取严格不等号。故式(13)成立。

以上从式(10)证得了式(13)。要说明式(10)和式(13)等价，以下只需从式(13)证得式(10)。事实上，由Hölder不等式，可知：

(16)

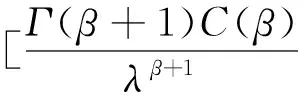
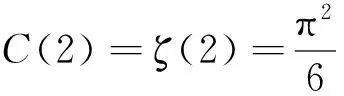
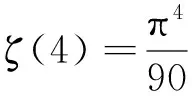
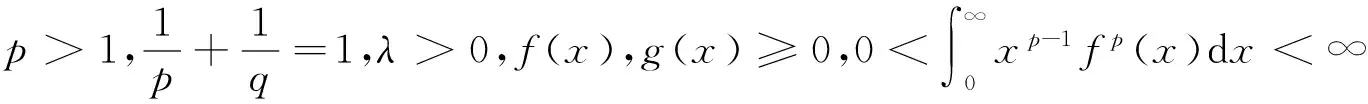
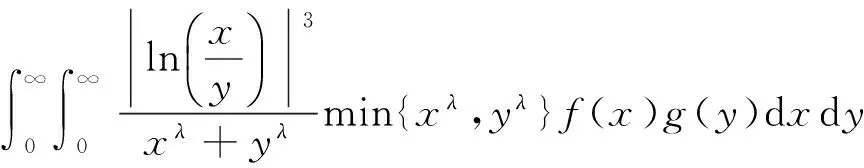
若在定理1中,令β=0,λ=1，则有推论2。

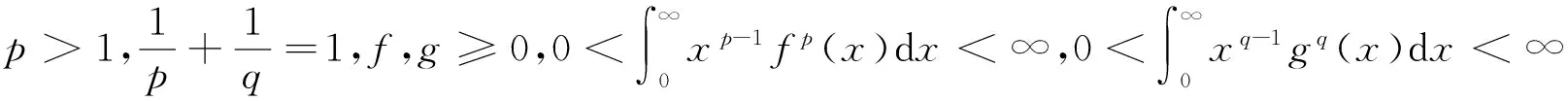
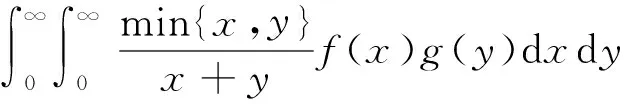
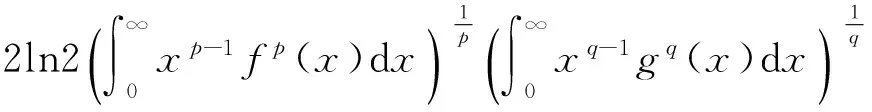
2　结　语

通过引入参数，借助分析的技巧，本文建立了一个混合核的Hilbert型积分不等式，在一定程度上

推广了前人已有的结果，这具有一定的价值。另外，本文研究的仍然是零齐次核的Hilbert型积分不等式，能否将积分核推广到负齐次核或者是非齐次核的情形，仍然是值得研究的问题。

[1]HARDYGH,LITTLEWOODJE,PolyaG.Inequalities[M].Cambridge:Cambridgeuniversitypress, 1952: 255.

[2]MINTRINOVICDS,PECARICJE,FINKAM.Inequalitiesinvolvingfunctionsandtheirintegralsandderivatives[M].Boston:KluwerAcademic, 1991: 79-135.

[3] 刘琼，龙顺潮.一个推广的Hilbert型积分不等式[J]. 数学物理学报:A辑, 2014, 34(1): 179-185.

[4] 陈小雨，高明哲，黄政. 具有Catalan常数的Hilbert型积分不等式[J].南京大学学报: 数学半年刊，2013, 30(1)：95-103.

[5]KUANGJ,DEBNATHL.OnnewgeneralizationsofHilbert'sinequalityandtheirapplications[J].JournalofMathematicalAnalysisandApplications, 2000, 245(1): 248-265.

[6]JINJJ.AnewgeneralizationofHardy-Hilberttypeinequalitywithmulti-parameters[J].JournalofMathematicalResearchwithApplications, 2009, 29(6): 1131-1136.

[7]JINJJ.OnHilbert’stypeinequalities[J].JournalofMathematicalAnalysisandApplications, 2008, 340(2)：932-942.

[8] 杨必成. 一个较为精密的Hardy-Hilbert型不等式及其应用[J].数学学报，2006, 49(2)： 363-368.

[9] 和炳.一个含零齐次核的Hardy-Hilbert型积分不等式[J].浙江大学学报(理学版)，2011, 38(4)： 380-383.

[10] 菲赫金哥尔茨TM. 微积分学教程: 第二卷[M].徐献瑜，冷生明，梁文骐，译. 2版.北京：高等教育出版社，2006: 625-639.

[11] 匡继昌. 常用不等式[M].3版. 济南：山东科学技术出版社，2003: 5.

(责任编辑： 康锋)

On Generalization of A Hilbert-type Integral Inequality

YOUMinghui

(Mathematics Teaching and Research Section，Zhejiang Institute of Mechanical and Electrical Engineering, Hangzhou 310053, China)

By introducing parameters, and using the method of real analysis, we establish a Hilbert-type integral inequality with the optimal constant factor and consider its equivalent form. Moreover, we also generalize the results of relevant literatures.

Hilbert-type inequality；equivalent form；Hölder inequality；Riemann Zeta function；Gamma function

10.3969/j.issn.1673-3851.2016.01.025

2015-04-19

有名辉(1982-)，男，浙江安吉人，讲师,硕士，主要从事解析不等式方面的研究。

O178

A

1673- 3851 (2016) 01- 0150- 04 引用页码： 010805