时滞群体竞技体育模型的稳定性与Hopf分支研究

曾清娟，马亚萍，路秋英

(浙江理工大学数学系，杭州 310018)



时滞群体竞技体育模型的稳定性与Hopf分支研究

曾清娟，马亚萍，路秋英

(浙江理工大学数学系，杭州 310018)

提出了一种带有时间滞后作用的群体竞技体育模型，通过时滞微分方程理论及Hopf分支理论，研究时滞因素对群体竞技体育活动的影响。首先计算时滞微分方程的线性化系统，得到线性化系统特征方程根的分布情况，进而得到平衡点稳定性发生改变的条件及局部Hopf分支的存在性。利用Matlab软件在时滞的临界点附近对系统正平衡点的稳定性及Hopf分支产生的周期振动进行了数值模拟，验证了理论结果的可靠性。

平衡点；稳定性；时滞；Hopf分支；数值模拟

0　引　言

微分方程建模最早可以追溯到Multhus的早期人口模型、Lotka和Volterra的捕食者-食饵模型。这些模型一度被用来更好地发现和理解各种生物现象和社会问题。然而，过于简单的模型很难准确反映观察到的各种复杂动力学行为，如周期解的存在性就是其中之一，为此需要不断对模型进行改进。一种方法是不断提高方程的维数，然而代价是成倍增加的参数，很难通过实际数据给出估计；另外一种办法是考虑时间的滞后效应。时滞效应普遍存在于现实问题中，时滞可以对应疾病的潜伏期、输送延迟、反应延迟等。而且简单的时滞微分系统往往包含了丰富的复杂动力学行为。例如，宋永利等[1]研究了时间滞后效应的基因调控模型，王新秀[2]对具有时滞的Volterra捕食系统进行了Hopf分支研究，王志丽等[3]讨论了一类具有时滞和收获的捕食模型的稳定性和Hopf分支。尽管时滞微分系统的研究具有重要意义，然而直到20世纪60年代，这方面的研究主要集中在稳定性、有界性、渐进性及平衡态、周期解及概周期解的震荡性方面。与普通常微分系统相比，分支理论方面的研究相对较少。Hale[4]最早研究时滞微分系统的局部分支，他研究了时滞微分系统中心流型的存在性及Hopf分支定理。然而Hale的理论难以应用于实际问题。对于有限时滞的时滞微分系统，我们期望根据线性系统的特征根的情况来了解系统的稳定性和Hopf分支情况。由于线性系统的特征方程是关于时滞的函数，因此特征根也是时滞的函数。而且随着时滞的改变，奇点的稳定性会随之发生改变，从而在一些临界值附近会产生Hopf分支。此外，对部分时滞微分方程，随着时滞变化奇点出现从稳定到不稳定、再到稳定这种交替出现的现象，这种现象就是所谓的稳定开关现象[5]。对于时滞个数为1的情况，Cooke等[6]最早进行了研究。本文亦针对时滞个数为1的群体竞技体育活动模型进行研究。

杨水龙[7]提出了一种群体竞技体育活动的常微分方程模型。这里的竞技活动是指参加者必须具有一定的技能而非指专业竞技体育活动。该文将总的人类群体分为三类：Ⅰ.无参加体育活动的技能，但可以发展为参加活动的人，用p1(t)表示；Ⅱ.有参加体育活动的技能且本人愿意参加体育活动，用p2(t)表示；Ⅲ类有参加体育活动的技能而不愿参加者，用p3(t)表示。同时，将三类人总数设为1,则得到群体竞技体育活动的常微分方程模型如下：

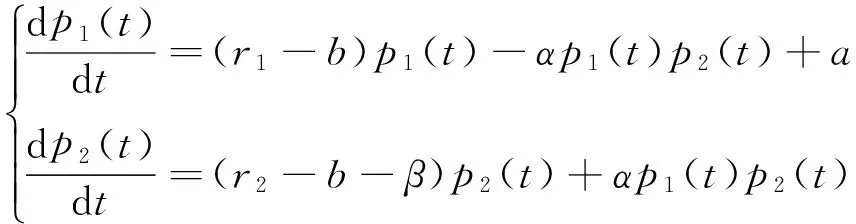
其中，α表示第Ⅰ类个体在第Ⅱ类个体影响下转化为第Ⅱ类个体的转化率；β表示第Ⅱ个体转化为第Ⅲ类个体的转化率，这里假定第Ⅲ类个体没有影响作用；a,b分别表示出生率和死亡率；ri(i=1,2)分别表示第Ⅰ、Ⅱ类个体的迁移率。

由于群体竞技体育要求参加者具有一定的竞技技能，因此对于无体育技能而又想发展成为可以参加活动的人，必须接受一定的培训和训练；培训和训练导致无参加体育活动技能的个体转化为具有参加体育竞技的个体必然需要一定的时间。上述模型[7]没有考虑时间滞后效应，本文对此进行改进，提出了一种具有时间滞后效应的时滞群体竞技体育活动模型。本文通过时滞微分方程理论和Hopf分支理论，讨论了平衡点的稳定性和由平衡点“失稳”引发Hopf分支产生的周期解的存在性，最后借助Matlab软件对理论结果进行了模拟和验证。

1　改进后的模型

考虑到参加体育活动技能的个体转化为具有参加体育竞技的个体需要一定的时间，设为τ，则改进后的时滞微分方程模型可以表示为：

(1)

其中：x,y,z分别表示Ⅰ类、Ⅱ类、Ⅲ类个体在时刻t的总数；α表示第Ⅰ类个体在第Ⅱ类个体影响下转化为第Ⅱ类个体的转化率；β表示第Ⅱ个体转化为第Ⅲ类个体的转化率，这里假定第Ⅲ类个体没有影响作用；a,b分别表示出生率和死亡率；ri(i=1,2,3)分别表示第Ⅰ、Ⅱ、Ⅲ类个体的迁移率。由于三类群体总人数之和保持不变，所以只须考虑上述由Ⅰ、Ⅱ类个体构成的二维系统。

2　平衡点的稳定性及Hopf分支的存在性

首先计算系统的平衡点。

2.1边界平衡点E0的渐近稳定性

H1：b-r1>0，

则边界平衡点为非负平衡点。那么系统(1)在平衡点E0(x0,0)处的线性化系统为：

(2)

(3)

(λ-m1)(λ-m2-m3e-λτ)=0

(4)

根据假设H1，显然λ=m1=r1-b总是方程(4)的负根，所以接下来研究特征方程(4)的第二个因子λ-m2-m3e-λτ。

令

G(λ)=λ-m2-m3e-λτ

(5)

如果m3<-m2成立，当τ=0时，即没有时滞影响，可参考文献[7]，可知系统在边界平衡点是渐近稳定的。下面考虑τ>0的情况。

引理1当τ>0 时，如果m3<-m2成立，特征方程(4)没有纯虚根。

证明：假设λ=iω(ω>0) 为特征方程(4)的一个纯虚根，将λ=iω 代入方程(4)，并分离实部虚部，得到如下方程：

(6)

平方相加，得到

矛盾，即对任意τ≥0，方程(4)没有纯虚根，也就是说特征方程的零点不会出现在虚轴或者穿过虚轴。

综合以上的分析，当系统满足假设H1时，对于任意τ≥0，可得到的结论如下：

a)如果m3>-m2，E0(x0,0)不稳定；

b)如果m3<-m2，E0(x0,0)局部渐近稳定。

2.2正平衡点E*(x*,y*) 的渐近稳定性

引理2 假设H2：b-r2+β>0,aα+(r1-b)(b-r2+β)>0成立，则系统(1)显然有唯一的正平衡点E*(x*,y*)。

系统(1)在正平衡点E*(x*,y*) 处的线性化系统为：

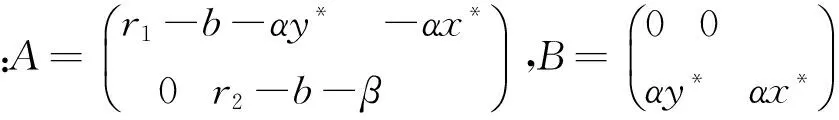
根据上式，可得到在正平衡点E*(x*,y*)的线性化系统为：

(7)

系统(7)对应的特征方程整理可得：

λ2+(p0λ+p1)e-λτ+q0λ+q1=0

(8)

其中：p0=-αx*，q0=(b-r1+αy*)-(r2-b-β)，p1=αx*(r1-b)，q1=(r1-b-αy*)(r2-b-β)。

引理3假设条件H2成立，并且有

H3:q1-p1=aα-(r1-b)(b-r2+β)<0，

则当τ从零增加时，存在τ0使得当τ∈[0,τ0)时，正平衡点E*局部渐近稳定；当τ>τ0时E*不稳定；而当τ=τj时，系统(1)在正平衡点E*附近产生Hopf分支。

证明：首先证明特征方程在正平衡点E*处存在一对纯虚根±iω0,ω0>0。

当τ=0 时，式(8)整理可得：

λ2+(p0+q0)λ+(p1+q1)=0

(9)

对于上述无时滞条件下的讨论可参考文献[7]，得知当τ=0时，正平衡点E*渐近稳定。下面讨论τ>0的情况。

当τ>0时，如果λ=iω(ω>0) 为特征方程(8)的纯虚根,代入并分离实部虚部得：

(10)

由方程组(10)消去三角函数，可以得到：

(11)

其中：

(12)

若又有

H3:q1-p1=aα-(r1-b)(b-r2+β)<0

成立，同时由(12)知方程(11)存在唯一正实根ω0，则当τ=τj,j=0,1,2,… 时方程(8)存在一对互为共轭的纯虚根±iω0。

根据方程组(10)可得到：

(13)

结合(10)、(11)、(12)，定义

(14)

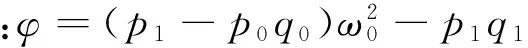
那么，(τ,λ)=(τj,iω0)满足方程(8)。

定义

λ(τ)=α(τ)+iω(τ)

(15)

为特征方程(8)的一般形式的根，且有：

α(τj)=0,ω(τj)=ω0。

(16)

因此，

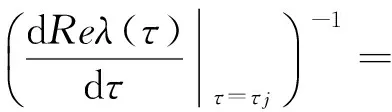
三是严守纪律，守住底线。要加强政治纪律、工作纪律，尤其是中层以上干部，一定要有底线意识，要合法合规做事，牢牢守住法律这根红线，讲政治、守规矩、做表率，杜绝任何违规违纪现象。要认识到位，执行力到位，用制度管事，推动各项工作落地见效。要坚持安全发展理念，坚守安全红线，筑牢发展底线，落实责任，强化措施，务求实效，为企业发展提供强有力的安全保障。

其中：M=p0cosωτ，N=2ω-p0sinωτ，X=-p0ω2cosωτ+p1ωsinωτ，Y=p0ω2sinωτ+p1ωcosωτ.

根据(13)式可推导得下式成立：

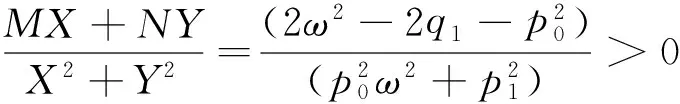
从而证明了横截性条件成立。

因此，Hopf分支在ω=ω0，τ=τj处发生，证毕。

2.3系统的Hopf分支

综上所述，关于时滞，系统在τ=τj发生稳定性改变。从而根据Hopf分支理论得到该时滞群体竞技体育活动模型(1)在其正平衡点E*(x*,y*)处发生Hopf分支。

定理1设系统(1)满足条件H2、H3，且ω0、τj(j=0，1,2……)如(13)、(14)所定义的，则：

b) 时滞τ=τj,j=0,1,2,…是系统(1)在正平衡点E*处的Hopf分支值。

3　数值模拟

选取一组参数如下：

a=0.012,α=0.38,r1-b=0.21,

r2-b-β=-0.126.

则根据前面的分析及公式，经计算得到

p0=-0.1260,q0=0.1622,

p1=0.0265,q1=0.0046.

E*(x*,y*)=(0.3316,0.6479)，

ω2=0.1594;ω=0.0254，

τ0=1.5222.

通过Matlab软件绘图，对于系统(1)，得到：当时滞τ=1.3<τ0时的数值模拟结果，得到系统的数值解的波形图和平面相图，见图1和图2；当时滞τ=1.56>τ0时的数值模拟结果，同上，见图3和图4。

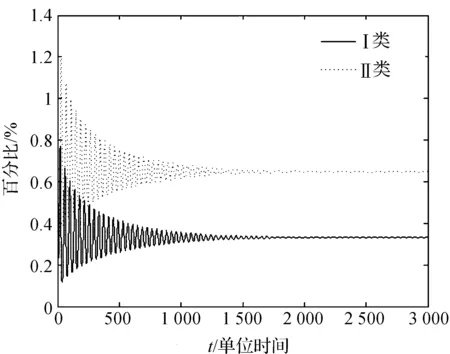
图1　Ⅰ类和Ⅱ类人群占总人数的百分比关于时间的波形图注：其中初值取(0.1,0.6)，τ=1.3<τ0=1.5222。

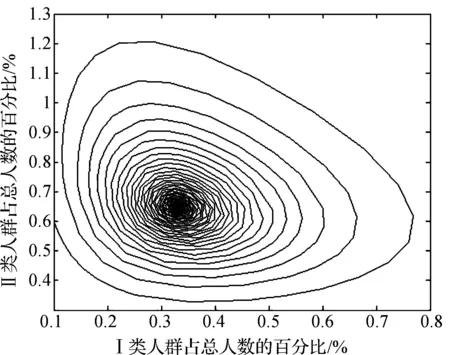
图2　Ⅰ类和Ⅱ类人群的平面相图注：其中初值取(0.1,0.6)，τ=1.3<τ0=1.5222。

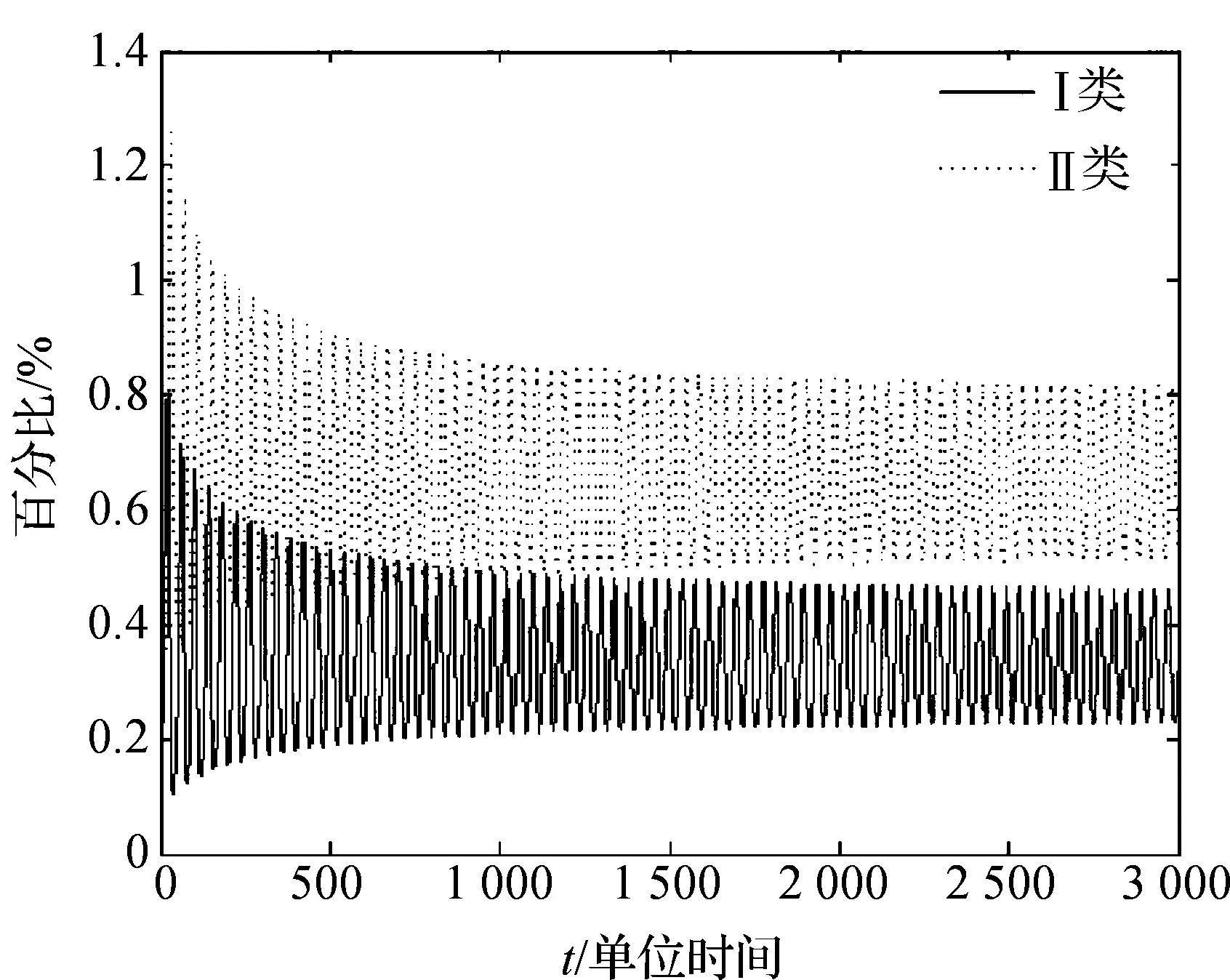
图3　Ⅰ类和Ⅱ类人群占总人数的百分比关于时间的波形图注：其中初值取(0.1,0.6)，τ=1.56>τ0=1.5222。

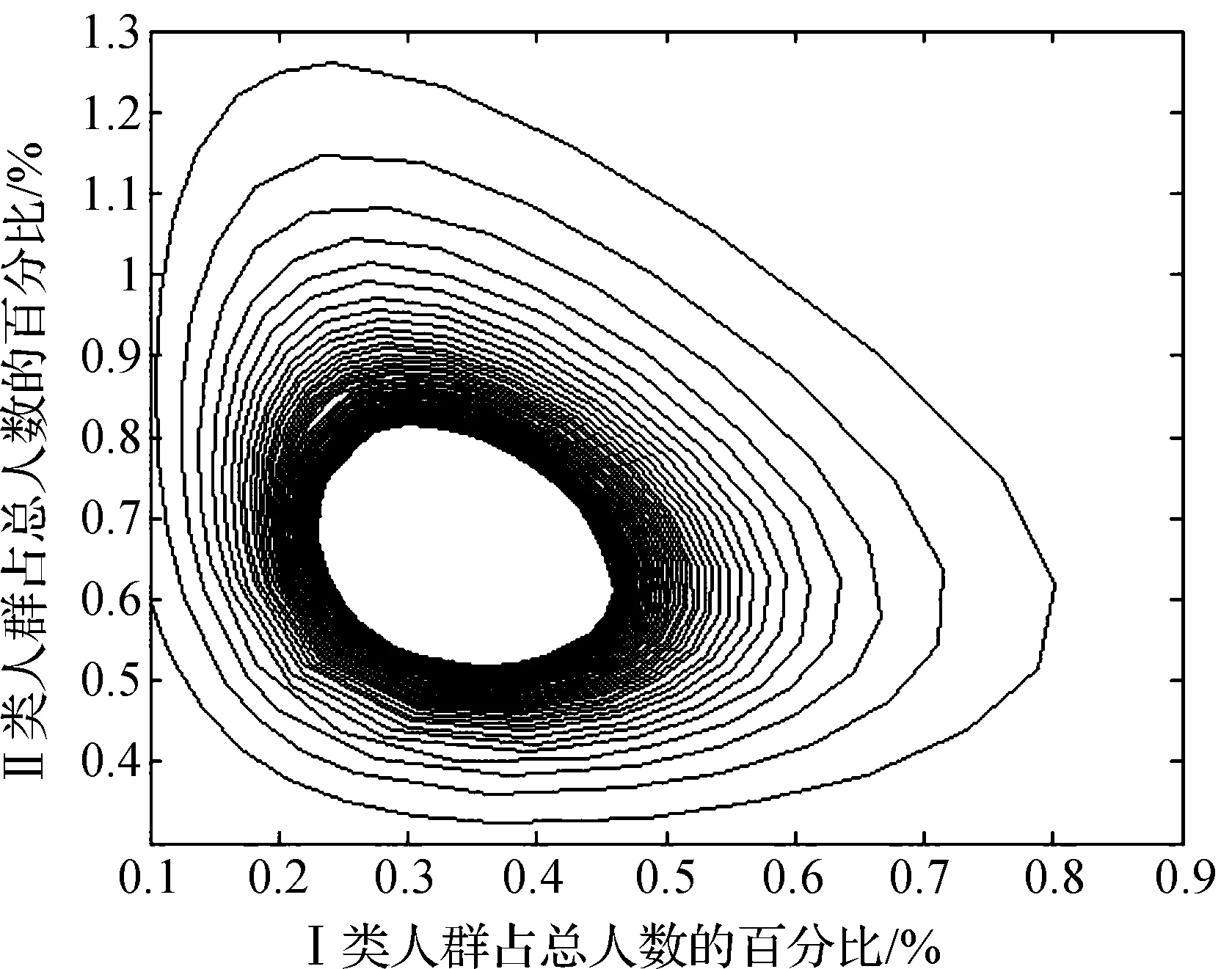
图4　Ⅰ类和Ⅱ类人群人数的平面相图注：其中初值取(0.1,0.6)，τ=1.56>τ0=1.5222。

通过Matlab数值模拟，可以清楚看出正平衡的稳定性随着时滞的改变发生了变化。取初始值为(x0,y0)=(1,1)，当τ=1.3<τ0，系统(1)的正平衡点E*局部渐近稳定(图1和图2)；当 τ=1.56>τ0时，系统(1)的正平衡点E*不稳定(见图3和图4)；当τ=τ0时，系统(1)在正平衡点E*附近存在Hopf分支周期解。因此，对时滞群体竞技体育模型，本文得到无参加体育活动技能但可发展为参加活动的人群与具有参加体育活动技能且本人愿意参加体育活动的人群之间存在周期性的变化。这与理论的分析结果一致。

4　总　结

本文研究了一类时滞群体竞技体育活动模型。首先，通过理论分析可以得到时滞群体竞技体育活动模型对时滞τ存在稳定性开关。当时滞τ从0不断增加的过程中，存在某些临界值点，在这些临界点处系统平衡点的稳定性总是由稳定变到不稳定，即τ从零增加每通过临界值时，从正平衡点分支出周期解。其次，通过Matlab软件对时滞群体竞技体育活动模型进行了数值模拟，通过选取一组参数，验证了上述模型的理论结果。模型分析和数值模拟结果表明，对具有时滞作用的群体竞技体育模型，无参加体育活动技能但可发展为参加活动的人群Ⅰ和具有

参加体育活动技能且本人愿意参加体育活动的人群Ⅱ之间存在周期性的动态平衡。

[1] 宋永利, 叶子. 时滞基因调控模型的稳定性与 Hopf 分支[J]. 同济大学学报: 自然科学版, 2013, 41(4): 630-636.

[2] 王新秀. 具有时滞的Volterra捕食系统的Hopf分支分析[D]. 兰州: 西北大学, 2010：16-32.

[3] 王志丽, 徐瑞. 一类具有时滞和收获的捕食模型的稳定性和Hopf分支[J]. 北华大学学报: 自然科学版, 2014, 15(1): 1-6.

[4] HALE J . Functional differential equations[M]. Berlin: Springer Verlag , 1977: 9-22.[5] Kuang Y. Delay differential equations with applications in population dynamics[M]. Boston: Academic Press, 1993: 58-62.

[6] COOKE K L, GROSSMAN Z. Discrete delay, distributed delay and stability switches[J]. Journal of Mathematical Analysis and Applications, 1982, 86(2): 592-627.

[7] 杨水龙. 群体竞技体育活动常微分方程模型的稳定性与Hopf 分支[J]. 山西师范大学学报: 自然科学版, 2000, 14(4): 12-15.

(责任编辑： 康锋)

Stability and Hopf Bifurcation of Time-delay Group Competitive Sports Model

ZENGQingjuan,MAYaping,LUQiuying

(School of Science, Zhejiang Sci-Tech University, Hangzhou 310018, China)

This paper proposes group competitive sports model with time delay function. The influence of time delay on group competitive sports activities is studied through delay differential equation and Hopf bifurcation theory. Firstly, linearization system of delay differential equation is calculated to gain distribution of the corresponding characteristic equation root. Further, the conditions for the change in equilibrium point stability and the existence of Hopf bifurcation are obtained. Besides, Matlab software is applied to carry out numerical simulation of equilibrium point stability near the critical point of time delay and periodic vibration caused by Hopf bifurcation. The simulation result verifies the reliability of theoretical results.

equilibrium point; stability; time delay; Hopf bifurcation; numerical simulation

10.3969/j.issn.1673-3851.2016.01.026

2015-01-08

国家自然科学基金项目(11101370, 11211130093)，浙江理工大学“521人才培养计划” (11430132521304)

曾清娟(1990-)，女，湖南茶陵人，硕士研究生，主要从事微分方程与定性理论方面的研究。

路秋英，E-mail：qiuyinglu@163.com

O175.12

A

1673- 3851 (2016) 01- 0154- 05 引用页码： 010806