基于刚度连接双层调谐质量阻尼器的性能

曹黎媛, 李春祥

(上海大学 土木工程系，上海　200072)



基于刚度连接双层调谐质量阻尼器的性能

曹黎媛, 李春祥

(上海大学 土木工程系，上海200072)

提出了基于刚度连接的双层调谐质量阻尼器(SDTMD)装置。SDTMD是在双层调谐质量阻尼器(DTMD)的基础上，在主体结构与小质量块之间设置一个附加弹簧而构成。经定义SDTMD最优参数的评价准则，在频域内研究了质量比对SDTMD控制结构位移响应时最优参数和有效性以及冲程的影响；并与TMD、DTMD和基于阻尼连接双层调谐质量阻尼器(DDTMD)装置进行了比较。数值结果表明，SDTMD的控制有效性明显高于TMD、DTMD和DDTMD。

结构振动控制；基于刚度连接双层调谐质量阻尼器；优化；性能；地震

调谐质量阻尼器(Tuned Mass Damper, TMD)是一种有效的被动控制装置。TMD通过准确调整自身系统的频率和阻尼，将主结构振动系统的能量转移到TMD并由其耗散，从而抑制主结构的振动响应。TMD研究起源于1928年，Ormondroyd等[1]提出了动力吸振器思想。此后，TMD在工业界得到了迅速发展和应用。1977年，美国波士顿Hancock大厦和纽约花旗中心大楼先后安装了TMD，随后TMD开始应用于土木工程结构的振动控制。然而，在实际应用中，由于TMD的频率很难达到预期的最优调谐状态，因而其控制结构地震响应的有效性不高或不稳定。为改善TMD对结构振动控制的有效性和鲁棒性，Igusa和Xu[2]提出了采用不同频率的多重TMD(MTMD)概念；此后，众多学者对MTMD展开了深入的研究[3-7]。李春祥在MTMD的研究基础上，提出了双层调谐质量阻尼器(DTMD)[8]、基于刚度-阻尼器主动调谐质量阻尼器(SD-ATMD)[9]和基于刚度-阻尼器主动多重调谐质量阻尼器(SD-AMTMD)[10]等控制装置。DTMD具有与MTMD相当的优越性；而SD-ATMD和SD-AMTMD有效性近似达到ATMD和AMTMD有效性，但它们的最优调谐频率比和平均阻尼比有明显的变化。本文与上述不同的是：在主体结构与DTMD的小质量块之间设置一个附加弹簧，构成SDTMD新装置，以期进一步提升DTMD的有效性。

1　结构-SDTMD系统的动力方程及动力放大系数

结构-SDTMD系统的力学模型如图1(a)所示。

结构-SDTMD系统的动力方程可表示为：

(1)

(2)

(3)

图1(a)　基于刚度连接的双层调谐质量阻尼器Fig.1(a) Stiffness-connection based DTMD

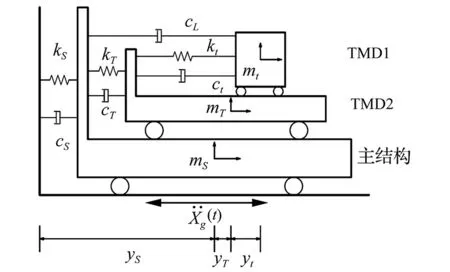
图1(b)　基于阻尼连接的双层调谐质量阻尼器Fig.1(b) damping-connection based DTMD

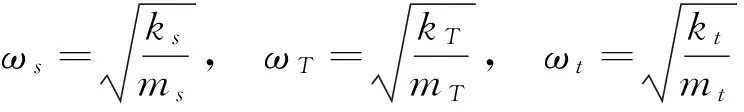
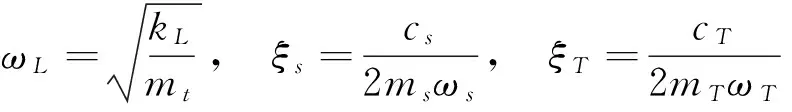
式中:ξs为主结构的阻尼比；ξT为TMD1的阻尼比；ξt为TMD2的阻尼比；μT为TMD1与主结构的质量比；μt为TMD2与主结构的质量比；η为TMD2与TMD1的质量比。

(4)

(5)

(6)

分别定义结构-SDTMD系统位移(ys)、TMD1冲程(yT)和TMD2冲程(yt)的动力放大系数：

(9)

式中：

ReT(λ)=D11Re(λ)-D12Im(λ)

ImT(λ)=D12Re(λ)+D11Im(λ)

Ret(λ)=D21Re(λ)-D22Im(λ)

Imt(λ)=D22Re(λ)+D21Im(λ)

C12=-2(1+η)ξtftλ

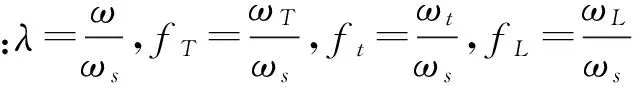
RHs=min.max.(DMFHs)

(10)

式(10)表示：使用GA算法，得到目标函数(式7)中位移动力放大系数DMFHs的最大值，在参数(fT、ft、fL、ξT和ξt)范围内，使最大DMFHs的最小化，从而获得最优的参数。

2　SDTMD的最优性能研究

根据SDTMD的最优参数评价准则，使用遗传算法(GA)，对SDTMD的性能进行数值分析。为比较，同时给出了TMD、DTMD(力学模型见文献[8])、DDTMD(力学模型如图1(b)所示)的数值结果。设fT=0.5～1.7，ft=0.0～1.4，fL=0.0～1.4，ξT=0～0.999，ξt=0～0.999，ξL=0～0.999，ΔfT=0.001，Δft=0.001，ΔfL=0.001，ΔξT=0.001，Δξt=0.001，ΔξL=0.001，λ=0～2，使用GA，得到μT=0.01和μT=0.02，η分别取0.25、0.5、0.75、1.0时，DMFHs、DMFHT、DMFHt、fT、ft、fL、ξT、ξt随η的变化曲线(图2-9)。因TMD仅有一个附加质量，为便于对比并确保与SDTMD的附加总质量保持一致，对应于SDTMD在不同μT取值时的η变化情况，将TMD取μT值分别修正为0.012 5、0.015、0.017 5、0.02与0.025、0.03、0.035、0.04。

由图2知，对结构—SDTMD系统，结构位移动力放大系数DMFHs随η增大而减小，意味着有效性越来越好。但当η>0.5时，总体上，增大η时SDTMD的控制有效性提高不明显。

由图3～4知，大质量块冲程DMFHT随η增大而减小。相对TMD、DTMD、DDTMD，SDTMD的大质量块冲程DMFHT有所减小；而小质量块冲程DMFHt则明显增大，这也是SDTMD有效性明显提高的原因。由μT=0.01和μT=0.02两种情况可看出，SDTMD小质量块冲程比大质量块冲程大；但实际中，η一般只采用0.5，所以SDTMD小质量块冲程是完全可以接受的。

图2　μT=0.01,0.02时TMD、DTMD、DDTMD、SDTMD的DMFHs随η变化趋势Fig.2 Variation trend ofDMFHswith respect to η for TMD, DTMD, DDTMD, and SDTMD in the case of μT=0.01,0.02

图3　μT=0.01,0.02时TMD、DTMD、DDTMD、SDTMD的DMFHT随η变化趋势Fig.3 Variation trend of DMFHTwith respect to η for TMD, DTMD, DDTMD, and SDTMD in the case of μT=0.01,0.02

图4　μT=0.01,0.02时DTMD、DDTMD、SDTMD的DMFHt随η变化趋势Fig.4 Variation trend of DMFHtwith respect to η for DTMD，DDTMD and SDTMD in the case of μT=0.01,0.02

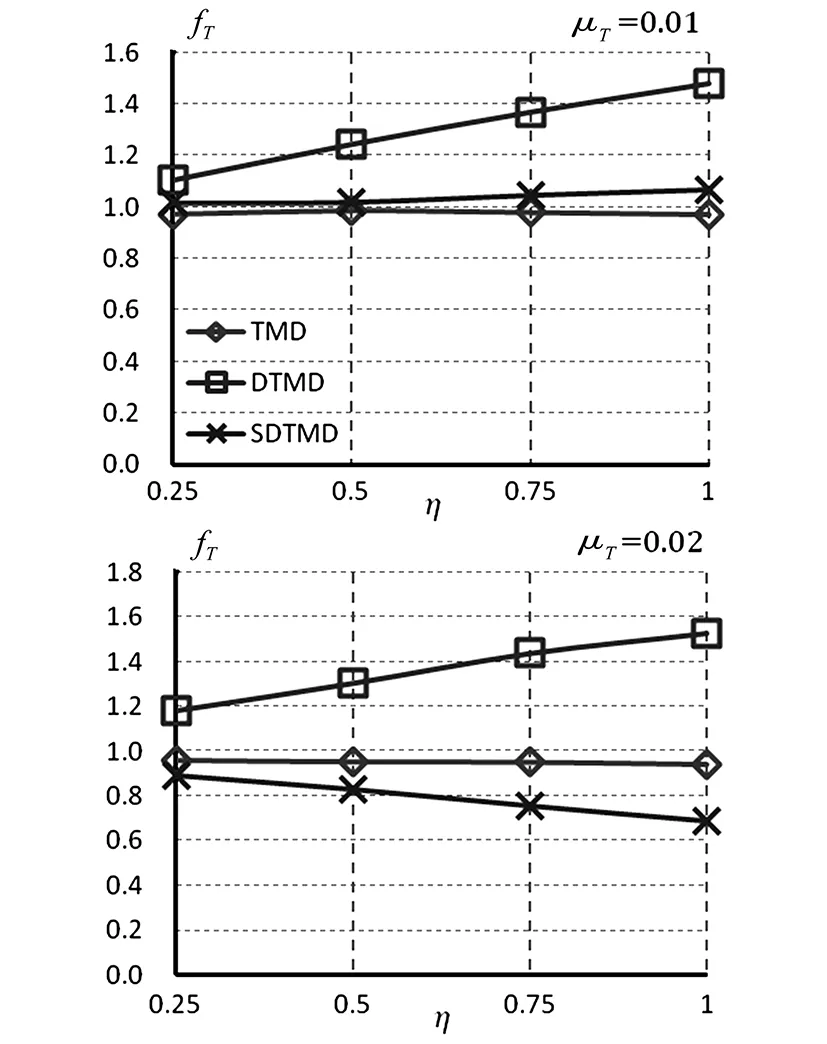
图5　μT=0.01,0.02时TMD、DTMD、SDTMD的fT随η变化趋势Fig.5 Variation trend of fT with respect to η for TMD，DTMD and SDTMD in the case of μT=0.01,0.02

图6　μT=0.01,0.02时DTMD和SDTMD的ft随η变化趋势Fig.6 Variation trend of ft with respect to η for TMD，DTMD and SDTMD in the case of μT=0.01,0.02

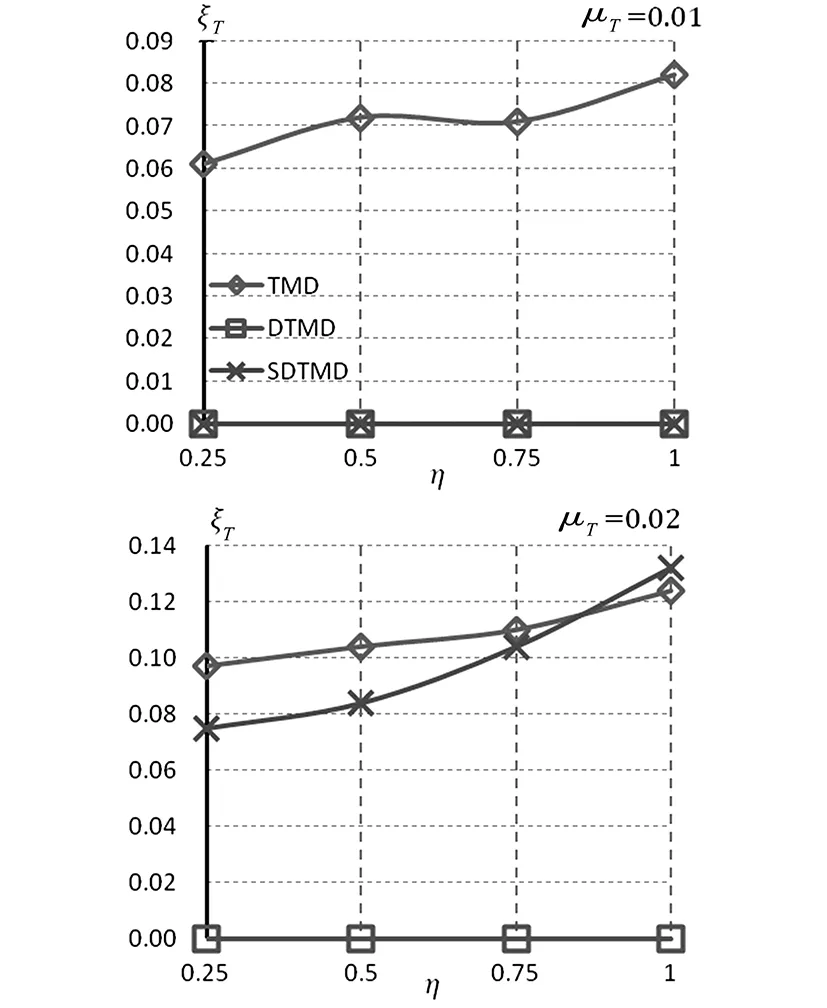
图7　μT=0.01,0.02时TMD、DTMD、SDTMD的ξT随η变化趋势Fig.7 Variation trend of ξT with respect to η for TMD，DTMD and SDTMD in the case of μT=0.01,0.02

由图5和图6知，当μT=0.01时，SDTMD的频率比fT随η的增大而增大，但不明显，在1.0～1.1之间取值；SDTMD的频率比fT略高于DTMD的，且明显小于TMD的。当μT=0.02时，SDTMD的频率比fT随η的增大而减小，变化相对较明显，取值范围为0.6～1.0；SDTMD的频率fT明显小于TMD和DTMD的。对于μT=0.01情况，SDTMD的频率比ft随η的增大而减小；当η>0.5时，增大η，ft变化不明显，取值范围为0.2～0.6。对于μT=0.02情况，SDTMD的频率比ft随η的增大而减小，总体变化不明显，取值范围为0.1～0.15。SDTMD的频率比明显小于DTMD的频率比。

由图7和图8知，μT=0.01时，SDTMD阻尼比ξT为0；μT=0.02时，SDTMD阻尼比ξT随η的增大而增大；当η>0.75时，SDTMD阻尼比超过了TMD，取值范围为0.06～0.14。对于μT=0.01，SDTMD阻尼比ξt随η的增大而增大，但明显小于DTMD阻尼比，取值范围为0.2～0.4；对于μT=0.02，SDTMD阻尼比ξt趋近于0，且明显小于DTMD阻尼比。

图8　μT=0.01,0.02时DTMD、SDTMD的ξt随η变化趋势Fig.8 Variation trend of ξt with respect to η for DTMD and SDTMD in the case of μT=0.01,0.02

由图9知，μT=0.01时，SDTMD频率比fL随η的增大而增大；当η>0.75时，fL随η的增大而减小，但变化不明显，取值范围为0.68～0.76。μT=0.02时，SDTMD频率比fL随η的增大而增大，取值范围1.02～1.06。

考虑到SDTMD控制的有效性、冲程以及参数的经济合理性这三个因素，经综合比较图2-9，本文建议选择表1中A和B两组数据。根据这2组参数设计的SDTMD，其控制有效性明显好于TMD和DTMD，而且参数和冲程都在合理、可接受的范围内。

图9　μT=0.01,0.02时SDTMD的fL随η变化关系曲线Fig.9 Variation trend of fL with respect to η for DTMD and SDTMD in the case of μT=0.01,0.02

组号ηfTftfLξTξtDMFHsDMFHTDMFHtA0.251.0190.5680.69700.2357.190146.588282.9357B0.51.0210.4290.75100.2196.536939.857473.2892

3　结　论

本文提出了基于刚度连接的双层调谐质量阻尼器(SDTMD)装置。通过推导及定义的SDTMD最优参数评价准则，使用遗传算法(GA)优化，在频域内数值研究了SDTMD的最优控制性能，并与TMD、DTMD、DDTMD进行了比较。数值结果表明，①SDTMD的有效性明显高于TMD、DTMD、DDTMD。②在实际中，建议η采用0.25或0.5，所以SDTMD小质量块冲程是完全可以接受的。③SDTMD最优频率比fT和ft都明显小于TMD、DTMD的相应值；而且μT=0.01时，fT在1.0～1.1和ft在0.2～0.6之间比较合适。④μT=0.01时，SDTMD的大质量块阻尼比为0，因此可以进一步简化装置。⑤随着质量比η的增加，SDTMD最优频率比fL存在极大值。此外，论文给出了SDTMD的最优设计参数表格，供设计时选择。

[1] Ormondroyd J, Den Hartog J P. The theory of the dynamic vibration absorber [J]. Transactions of the American Society of Mechanical Engineers，1928, 49, 50: A 9-22.

[2] Xu K, Igusa T. Dynamic characteristics of multiple substructures with closely spaced frequencies [J]. Earthquake Engineering and Structural Dynamics,1992,21(12): 1059-1070.

[3] Yamaguchi H, Harnpornchai N. Fundamental characteristics of multiple tuned mass dampers for suppressing harmonically forced oscillators [J]. Earthquake Engineering and Structural Dynamics, 1993, 22(1): 51-62.

[4] Jangid R S. Dynamic characteristics of structures with multiple tuned mass dampers [J]. Structural Engineering and Mechanics, 1995, 3(5): 497-509.

[5] Li Chun-xiang. Performance of multiple tuned mass dampers for attenuating undesirable oscillations of structures under the ground acceleration [J]. Earthquake Engineering and Structural Dynamics, 2000, 29(9): 1405-1421.

[6] Li Chun-xiang. Optimum multiple tuned mass dampers for structures under the ground acceleration based on DDMF and ADMF [J]. Earthquake Engineering and Structural Dynamics, 2002,31(4):897-919.

[7] 李春祥, 熊学玉, 程斌. 基于参数组合和加速度传递函数的最优MTMD研究 [J]. 振动与冲击, 2001, 20(3):50-54.

LI Chun-xiang, XIONG Xue-yu, CHENG Bin. The optimum MTMD based on parameter combinations and acceleration transfer function [J]. Journal of Vibration and Shock, 2001, 20(3): 50-54.

[8] Li Chun-xiang, Zhu Bil-ei. Estimating double tuned mass dampers for structures underground acceleration using a novel optimum criterion [J]. Journal of Sound and Vibration, 2006, 298(1/2): 280-297.

[9] 李春祥. 基于刚度-阻尼器ATMD模型的性能评价 [J]. 振动与冲击, 2004, 23(3): 14-23.

LI Chun-xiang. Performance assessment of stiffness-dashpot-based ATMD model [J]. Journal of Vibration and Shock, 2004, 23(3): 14-23.

[10] 李春祥. 基于刚度-阻尼器主动多重调谐质量阻尼器模型的性能评价[J]. 振动与冲击, 2004, 23(4):103-106.LI Chun-xiang. Performance assessment of modeling of stiffness-dashpot based active multiple tuned mass dampers [J]. Journal of Vibration and Shock, 2004, 23(4): 103-106.

Double-tuned-mass dampers based on stiffness connection

CAO Liyuan, LI Chunxiang

(Department of Civil Engineering, Shanghai University, Shanghai 200072, China)

Stiffness-connection-based double-tuned-mass dampers(SDTMD) were proposed here. Specifically, an added stiffness between the controlled structure and the smaller mass block in a DTMD was introduced to form a SDTMD. In order to obtain optimal parameters of SDTMD, an optimal criterion was defined. Employing this defined criterion, the influences of mass ratio on optimal parameters, effectiveness and stroke of SDTMD were studied numerically in frequency domain. Furthermore, the optimal performances of SDTMD were compared with those of TMD, DTMD, and damping-connection-based double-tuned-mass dampers(DDTMD). The numerical results showed that the effectiveness of SDTMD is remarkably higher than those of TMD, DTMD and DDTMD.

structural vibration control; stiffness-connection-based double-tuned-mass dampers(SDTMD); optimization; performance; earthquake

2015-05-19修改稿收到日期：2015-08-10

曹黎媛 女，研究生，1991年4月生

李春祥 男，博士，教授，博士生导师，1964年12月生

TU311

A

10.13465/j.cnki.jvs.2016.15.029