高层剪力墙隔震结构动力特性简化计算方法

王学庆， 赵　明

(安徽工业大学 建筑工程学院,安徽 马鞍山　243032)



高层剪力墙隔震结构动力特性简化计算方法

王学庆， 赵明

(安徽工业大学 建筑工程学院,安徽 马鞍山243032)

针对规则高层剪力墙隔震结构侧向变形特征，按楼层集中质量法建立的多质点模型进行模态分析，以振型有效质量为判断依据，确定了该类结构在采用振型分解反应谱法进行单轴向计算分析时可取前两阶振型。在考虑了隔震层转动影响前提下，基于所定义的线刚重比构建了该类结构前两阶自振周期、振型、振型阻尼比的简化计算方法及相应计算式，验证计算结果表明能够较好的反映出结构前两阶动力特性。当隔震层转动线刚重比较小时，若不计入其影响将导致二阶周期计算偏差较大。在此基础上给出了基于线刚重比的规则高层剪力墙结构隔震前后周期比的显式表达式，为高层隔震结构实用设计方法的研究提供了基础。

高层剪力墙结构；隔震；线刚重比；动力特性；简化计算

橡胶垫隔震技术能够通过延长结构自振周期减小上部结构地震作用效应而被广泛应用于中低层建筑，因其上部结构自身相对变形较小而可被视为刚体，故相应的计算分析可采用较为简化的单质点模型完成[1-3]。高层隔震结构的动力特性受上部结构影响较大，若采用单质点模型进行简化计算将导致较大偏差，若按楼层集中质量建立多质点模型进行计算又较为繁杂，不便于设计人员快速计算与分析。因此，简单有效的计算模型与方法对工程应用和相应的设计人员均有重要意义，国内外已有很多专家学者对此进行了相关研究。

祁皑等[4-6]先后采用单质点和三质点模型对高层隔震结构的高宽比限值进行了深入研究，计算表明不同模型所得结果存在一定差异，认为三质点模型所得高宽比限值更加安全可靠。刘文光等[7-8]先后采用单质点和双质点模型对高层隔震结构的地震响应单纯质点法研究，并对22层隔震结构工程实例进行了时程分析，结果表明单、双质点模型的单纯质点法均与多质点模型的计算结果相近。文献[9-10]对高层框架隔震结构开展了振动台试验研究，结果表明隔震能够降低结构高阶振型的反应，且在结构隔震设计中应考虑上部结构变形的影响，而文献[11]对特定的高层框架剪力墙结构进行的时域和频域分析也得出了类似结论。文献[12]将20层框架剪力墙隔震结构简化为多质点摆动模型进行了时程分析，认为平摆作用将导致上部结构各层加速度相应变大。以上高层隔震结构简化计算模型中，上部结构均存在较强剪切变形特征，难以反应剪力墙弯曲变形特点。而文献[13]则认为高层隔震结构可简化为隔震悬臂梁模型，但并未给出相应的等效方法及计算式，只能进行定性分析。

本文在计入隔震层转动影响前提下，基于所定义的线刚重比构建了适合高层剪力墙隔震结构前两阶自振周期、振型、振型阻尼比的简化计算方法及相应计算式，并通过对比计算验证了这种方法的简便有效性。

1　高层隔震结构的动力特征方程

1.1基本假设

(1) 隔震支座均匀对称布置；

(2) 上部结构各楼层层高均为h，因隔震层高度与上部结构高度相比较小，忽略不计；

(3) 上部结构各楼层等效重力荷载均为G0，隔震层等效重力荷载为GI，且Rg=GI/G0为常量。

1.2动力特征方程

高层剪力墙隔震结构由上部结构和隔震层组成。在侧向力的作用下，上部结构将发生弯曲变形，隔震层将发生剪切变形和转动变形，如图1所示。

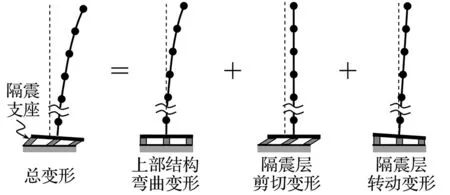
图1　高层剪力墙隔震结构侧向变形构成Fig.1 Lateral deformation component of high-rise isolated structure

根据图1中的侧向变形分解，采用柔度法建立的高层剪力墙隔震结构的动力特征方程为：

(1)

式中：[m]为质量矩阵，[f]为柔度矩阵，[I]为单位矩阵，ωj为结构第j阶自振圆频率，{φj}为与之对应的振型。

[m]为对角阵，主对角线上的元素分别为m11=RgG0/g与mii=G0/g，(i=2,3,…,n+1)，g为重力加速度，n为上部结构总层数；

[f]的具体构成为：

[f]=[fs]+[fIb]+[fIs]

(2)

[fs]为上部结构弯曲柔度分量的对称矩阵，其上三角中的元素为：

fsij=(i-1)2(3j-i-2)/(6n3RsGs)

(i，j=1,2,…,n+1)

(3)

式中：Rs=EJd/(H3Gs)为上部结构线刚重比，H=nh为上部结构总高度，Gs=nG0为结构等效总重力荷载，EJd为上部结构按倒三角形分布荷载作用下顶点位移相等原则等效的抗弯刚度，其计算方法请参见文献[14]。

[fIb]为隔震层转动柔度分量的对称矩阵，其上三角中的元素为：

fIbij=(i-1)(j-1)/(n2RIbGs)

(i，j=1,2,…,n+1)

(4a)

式中：RIb=KIb/(H2Gs)为隔震层的转动线刚重比，KIb为隔震层转动刚度。

(4b)

式中：Kvi为支座i的竖向压缩刚度，li为支座i到隔震层形心的距离，m为支座的个数。

[fIs]为隔震层剪切柔度分量矩阵：

fIsij=1/(RIsG)

(i，j=1,2,…,n+1)

(5a)

式中：RIs=KIs/G为隔震层的剪切线刚重比，KIs为隔震层剪切刚度，G=(n+Rg)G0。

(5b)

式中：Ksi为支座i的水平剪切刚度。

2　结构基本周期的简化计算

2.1上部结构基本周期的简化计算

当RIb→∞和RIs→∞时，式(1)即为上部结构的动力特征方程。对其进行分析可知，结构基本周期仅与层数n和线刚重比Rs有关。上部结构分别为10、20、30、40和50层五种工况的上部结构基本周期Ts与Rs的关系曲线如图2所示。

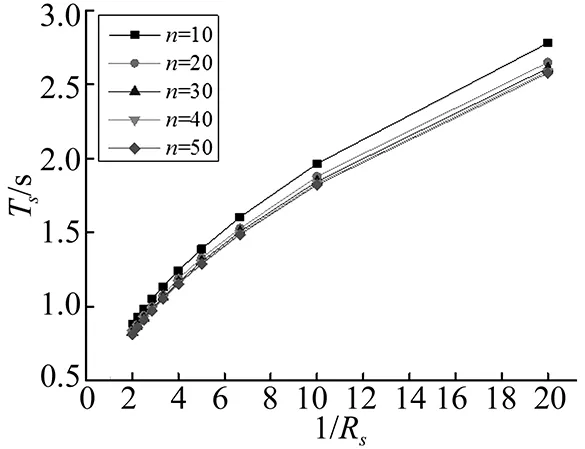
图2　Ts与1/Rs的关系曲线Fig.2 Relationship between Ts and 1/Rs

由上图可知，上部结构基本周期Ts与线刚重比Rs符合如下基本形式：

(6a)

式中：f(n)是随层数变化的系数，其与层数n的关系如图3所示。对其进行线性拟合可得：

(6b)

将式(6b)代入式(6a)，可得上部结构基本周期的简化计算公式为：

(6c)

由上式可知，若不考虑1+1/n项，基本周期计算值将偏小n/(1+n)，即n=10时小9%，n=30时小3.2%，n=50时小2%。因此，层数n可视为对上部结构基本周期的修正，而层数越多，其修正作用越小。

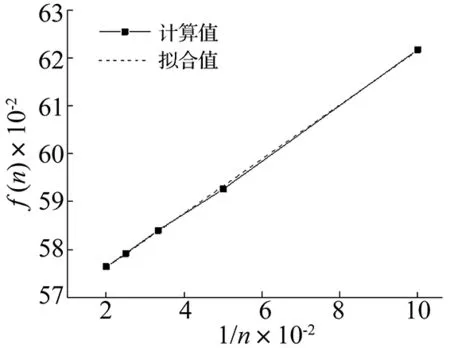
图3　f(n)与1/n的关系曲线Fig.3 Relationship between f(n) and 1/n

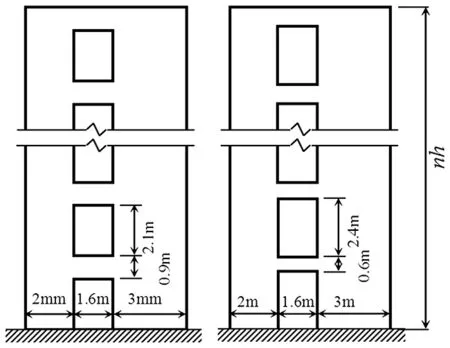
图4　剪力墙结构示意Fig.4 Sketch of shear wall structure

工况1234墙体类型小开口小开口双肢双肢墙厚/m0.350.300.250.2层数33282218EJd×107/(kN·m2)23.7220.1415.6311.95H/m99846654Gs×103/kN1.631.361.551.69Rs/1/m0.150.250.350.45上部结构基本周期Ts/s有限元1.511.171.010.90式(1)1.501.171.000.89式(6c)1.501.171.000.89

为验证上部结构基本周期简化计算式(6c)的准确性，分别与有限单元法和式(1)的层模型方法计算结果对比，如表1所示。图4为验证计算所选用的剪力墙结构示意图，其中图(a)为小开口剪力墙，图(b)为双肢剪力墙。取E=Ec=3.0×107kN/m2，Ec为混凝土弹性模量，剪切模量取G=0.42Ec，重力加速度g=10 m/s2。计算结果表明，利用式(6c)计算上部结构基本周期的误差基本在1%范围内，精度较高，能够满足工程需要，且计算简便。

2.2隔震层剪切变形时结构基本周期的简化计算

当Rs→∞和RIb→∞时，上部结构已成为刚体，隔震层仅有水平剪切变形。此时，高层剪力墙隔震结构则可简化为单自由度体系，且与层数n无关，其基本周期为：

(7)

图5为高层剪力墙隔震结构处于仅隔震层发生剪切变形时的基本周期简化计算式(7)与式(1)的对比计算结果及误差曲线，简化计算式的误差仅为0.05%左右。另由式(7)可知，当仅隔震层发生剪切变形时，其基本周期仅与RIs有关。

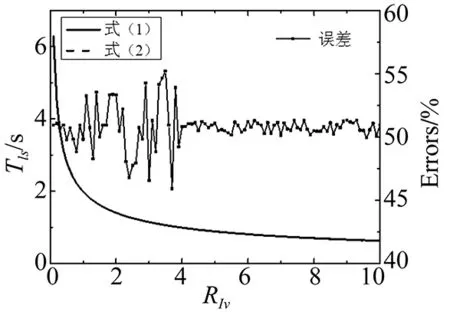
图5　式(7)验证Fig.5 Verification of formula(7)

2.3隔震层转动变形时结构基本周期的简化计算

当Rs→∞和RIv→∞时，由假定(1)可知，隔震层仅有绕其中性轴的转动变形，而上部结构仍为刚体。此时，高层剪力墙隔震结构仍则可简化为单自由度体系，其基本周期为：

(8)

上式中的层数n是计算上部结构对隔震层中性轴的转动惯量时引入的，若不考虑层数n的影响，当n=10时，其基本周期计算值将偏小7%，n=30时偏小2.4%，n=50时偏小1.5%。因此，层数n也可看作对结构基本周期的修正，且层数越多，其修正作用越小。

图6　式(8)验证Fig.6 Verification of formula(8)

图6为高层剪力墙隔震结构处于仅发生转动变形时的基本周期简化计算式(8)与式(1)的对比计算结果及误差曲线，当层数n取较小值与较大值时，基本周期的简化计算式的最大误差均处于0.05%左右，由此可见简化计算的偏差很小。

2.4前两阶自振周期的简化计算

结合式(1)及振型质量参与系数的定义可得高层剪力墙隔震结构第j阶振型质量参与系数为：

(9)

式中：mi为第i层质量，φji为经过对质量矩阵归一化处理的第j阶振型第i层振型位移。

若令γ1+2为高层剪力墙隔震结构前两阶振型质量参与系数和，则可由式(1)及式(9)计算出其随Rs、RIs和RIb变化的空间分布，如图7所示，因其为四维空间，故采用了切片图形方法，颜色的深浅程度代表γ1+2大小。由图可知，在考虑了隔震层转动刚度的影响后，高层剪力墙隔震结构前两阶振型质量参与系数和基本保持在95%以上。因此，该类结构单轴向反应谱分析时仅取前两阶振型即可得到较为满意的计算结果[13]。

另由图1可知，高层剪力墙隔震结构的前两阶振型均可看作上部结构与隔震层剪切、转动变形的一种组合，因此其前两阶自振周期的计算可简化为：

(10)

式(10)即符合高层剪力墙隔震结构的一般情况，同时也符合前述三种特殊状态。因此，作为自振周期的简化计算方法具有较高的统一性。

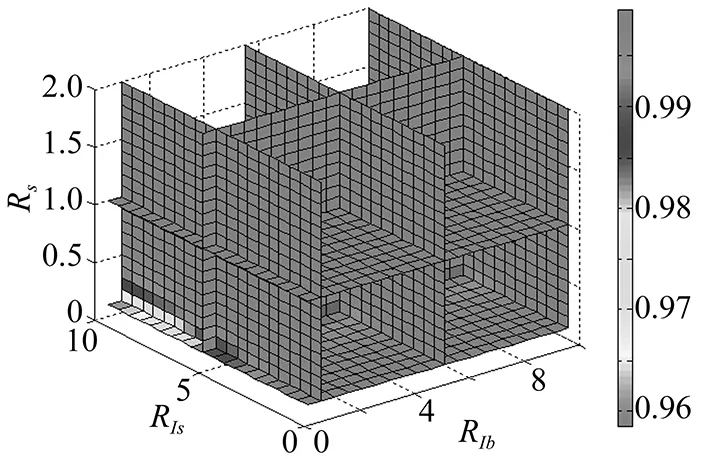
图7　γ1+2分布图Fig.7 The nephogram of γ1+2

依据文献[15]中对上部结构底层楼板的规定，取Rg=1.5；令Rs、RIs与RIb同为自变量，并考虑层数n分别取15、30和45层三种情况，再由式(6c)确定Rs的合理取值区间，验证高层剪力墙隔震结构基本周期的简化计算式(10)的准确性。

图8为式(6)、式(7)、式(8)及式(10)联合计算结果与式(1)计算结果相比的误差分布。由图可知，前两阶周期计算误差均出现在RIs/Rs较小及RIb/RIs较大的区域。一阶周期误差随层数增加而减小，最大误差不足1%；二阶周期误差则随层数增加而增加，最大不足9%。就总体而言，式(10)的计算精度是可以满足工程设计需要的。

图8　式(10)验证Fig.8 Verification of formula(10)

3　振型及阻尼比简化计算

3.1前两阶振型阻尼比简化计算

因高层剪力墙隔震结构可视为上部结构与隔震系统共同组成的结构体系，故其振型阻尼比可据文献[8]的双质点模型由下式确定：

(11a)

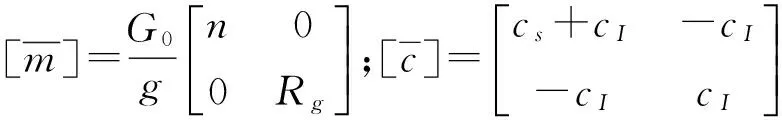
(11b)

(11c)

式中：ξeqi为第i个支座的等效阻尼比，ωt为试验确定ξeqi时的加载圆频率。

当层数n逐渐增大时，Rg/n→0，故上式在n较大时可进一步简化为：

ξj=Tj[μ2ξs/Ts+(1-μ)2ξI/TIs]

(j=1,2)

(11d)

3.2前两阶振型简化计算

由式(1)的计算结果可知，当T1/Ts≥1.5时，高层剪力墙隔震结构前两阶振型基本呈直线，因此可进行线性近似等效。

图9　振型Fig.9 Modal of vibration

(12a)

(12b)

在高层剪力墙隔震结构的地震作用效应中，通常较为关注基底剪力和倾覆力矩，分别用以估计隔震层的水平剪切变形、支座受拉和受压是否满足规范要求。由上述简化方法和式(1)分别计算出结构的动力特性后，采用振型分解反应谱法可分别得到基底剪力和倾覆力矩简化前后的对比误差曲面，如图10和图11所示，结果表明其受层数n的影响很小，可以忽略不计。与式(1)的计算结果相比，简化方法的基地剪力计算结果偏大，但最大不足7%，且随RIs/Rs和RIb/RIs的减小而减小，即T1/Ts越大误差越小。而由简化方法计算的倾覆力矩结果更为理想，其偏差均小于1.5%。因此，上述高层剪力墙隔震结构前两阶自振周期、振型及阻尼比的简化计算方法可应用于工程结构设计与分析中。

图10　基底剪力误差Fig.10 Errors of base shear

图11　倾覆力矩误差Fig.11 Errors of overturning moment

4　高层结构隔震前后周期比

(13a)

式中：λ1与λ2可由式(6c)、式(7)和式(8)表达为：

(13b)

由上式可知，高层结构隔震后与隔震前周期比除受Rs/RIs与Rs/RIb的影响外，还与层数n有关，但n对T1/Ts和T2/Ts的计算结果影响非常小，故可作以上近似。若不考虑隔震层转动刚度的影响(RIb→∞)，当给定高层结构隔震后与隔震前基本周期比T1/Ts，即可由式(13a)解出与之对应的Rs/RIs，并进一步确定隔震层水平剪切刚度，用以指导设计。

图12　T1与T2计算误差Fig.12 The calculation errors of T1 and T2

图12为计入与未计入RIb计算所得的前两阶周期误差曲线。二者相比，RIb对高层剪力墙隔震结构二阶周期的影响更为显著。T1的误差受周期比T1/Ts的影响很小，随RIb/RIs的增加而减小。当RIb≥2.5RIs时，T1的误差可控制在Ts×5%范围内。T2的误差受周期比T1/Ts的影响较大，且随其增加而增大，T1/Ts为1.5、2.0和2.5时，需要RIb分别大于2.5RIs、7RIs和14RIs才可使T2的误差控制在Ts×5%以内。因此，对于高层剪力墙隔震结构仅考虑隔震层的剪切刚度，忽略转动刚度的影响，将导致前两阶周期计算结果偏小。

5　实例分析

通过某一实际工程的有限元模拟及简化方法计算的对比分析，验证后者的正确性。该工程为22层剪力墙结构，层高3.3 m，剪力墙厚度250 mm，混凝土弹性模量Ec=3.0×104MPa，高宽比4.54，支座型号及布置如图13所示。地震波分别选用Kobe(PGA=0.345 g)、Chi_Chi(PGA=0.364 g)和NorthRidge(简称为N_R波，PGA=0.568 g)，结构地震响应时程有限元计算采用ANSYS建模。

图13　隔震支座布置图Fig.13 Arrangement of lead rubber bearings

由表3可知，不考虑与考虑隔震层转动的计算结果相比都是偏大的，Chi_Chi波作用下由简化方法得到的底部剪力和倾覆力矩增加最多，分别为10%和8.9%，相应的有限元方法增加均未超过5%，可见不考虑隔震层转动对结构底部剪力及倾覆力矩的影响并不大，且更加偏于保守。其结果偏大较小的原因在于，满足文献[16]中对支座拉压应力限值的前提下，支座的压缩变形量将很小，进而隔震层的转角也将很小。因此，在初步设计阶段可忽略隔震层转动的影响。

表2　结构参数

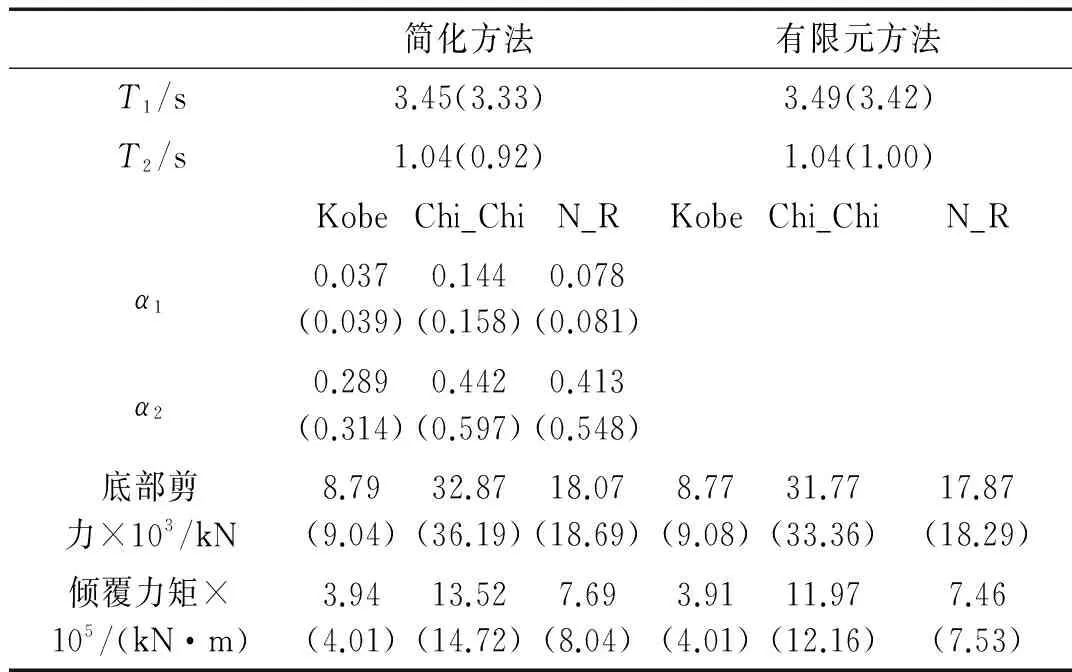
表3　计算结果对比

注：据式(11)计算的ξ1=0.09(0.08)；ξ2=0.1(0.11)；α1和α2分别为与之对应的加速度反应谱谱值。括号中数值为不考虑隔震层转动影响的结果。

简化方法计算结果与有限元时程分析结果相比，Kobe波的底部剪力偏大0.2%、倾覆力矩偏大0.8%；Chi_Chi波的分别偏大3.5%和12.9%；NorthRidge波的分别偏大1.1%和3%；表明简化方法的计算结果是更偏于安全的，能够满足工程结构初步设计的要求。因此，本文便捷有效的简化计算方法可以在高层隔震剪力墙结构的初步设计中应用。

6　结　论

将规则高层剪力墙隔震结构的侧向变形视为由上部结构的弯曲变形、隔震层的水平剪切变形和转动变形共同构成，并在必要的基本假设前提下，对该类结构的动力特性简化计算方法进行了分析与验证，得出以下主要结论：

(1) 在考虑了隔震层转动变形的影响后，高层剪力墙隔震结构前两阶振型质量参与系数和基本保持在95%以上。因此，该类结构单轴向反应谱分析时仅取前两阶振型即可得到较为满意的计算结果；

(2) 不考虑隔震层转动变形对高层隔震剪力墙结构底部剪力及倾覆力矩的影响并不大，故在初步设计阶段可忽略隔震层转动的影响。

(3) 基于线刚重比并考虑了隔震层转动变形的前两阶自振周期、振型和阻尼比的简化计算式，能够较为准确的估计基底剪力与倾覆力矩等重要的结构地震作用效应，为高层剪力墙隔震结构的设计与分析提供了快速计算方法。

[1] 王焕定,付伟庆,刘文光,等. 规则隔震结构等效简化模型的研究[J]. 工程力学, 2006,23(8): 138-143.

WANG Huan-ding, FU Wei-qing, LIU Wen-guang, et al. Research on equivalent simplified model of regular shock-insulation building [J]. Engineering Mechanics,2006,23(8): 138-143.

[2] Kelly J M. Earthquake resistant design with rubber [M]. Second Edition,Springer Verlag London Limited, 1997.

[3] Li Zhong-xi, Zhou Xi-yuan. Vibration property and earthquake response analysis method for regular isolated building [J]. Earthquake Engineering and Engineering Vibration,2002, 22(2): 33-41.

[4] 祁皑,范宏伟.基础隔震结构高宽比限值研究[J]. 建筑结构学报, 2004, 25(6): 52-58.

QI Ai,FAN Hong-wei. Research on the heigh-width ratio of base isolated structure[J]. Journal of Building Structures,2004, 25(6): 52-58.

[5] 祁皑,商昊江.高层基础隔震结构高宽比限值分析[J]. 振动与冲击, 2011,30(11): 272-280.

QI Ai，SHANG Hao-jiang, Analysis on limit of height-width ratio of high-rise base-isolated structure[J]. Journal of Vibration and Shock,2011,30(11): 272-280.

[6] 祁皑,徐翔,范宏伟.高层隔震结构高宽比限值研究[J]. 建筑结构, 2013,43(6):50-53.

QI Ai，XU Xiang，FAN Hong-wei. Study on height-width ratio of high-rise isolated buildings[J]. Building Structure, 2013,43(6): 50-53.

[7] 刘文光,刘阳, 杨巧荣,等. 高层隔震结构单质点模型的地震响应单纯质点法研究[J]. 振动工程学报,2012,25(6):693-698.

LIU Wen-guang, LIU Yang, YANG Qiao-rong, et al. A study on pure mass model method for seismic response of single mass model of high-rise isolated structure[J]. Journal of Vibration Engineering,2012,25(6): 693-698.

[8] 刘阳,刘文光,何文福,等. 高层隔震结构双质点模型的地震响应单纯质点法研究[J]. 振动与冲击, 2013,32(1): 8-13.

LIU Yang，LIU Wen-guang，HE Wen-fu，et al. Seismic response of a high-rise isolation structure 2-mass model with pure mass method[J]. Journal of Vibration and Shock,2013,32(1): 8-13.

[9] 何文福,霍达,刘文光,等.高层隔震结构振动台试验及数值分析[J]. 北京工业大学学报, 2010,36(3): 334-339.

HE Wen-fu, HUO Da, LIU Wen-guang, et al. Experimental study and numerical analysis of high rise isolated structure[J]. Journal of Beijing University of Technology,2010,36(3):334-339.

[10] 李昌平,刘伟庆,王曙光,等. 高层隔震和非隔震结构振动台试验对比[J]. 南京工业大学学报:自然科学版, 2013,35(2): 6-10.

LI Chang-ping，LIU Wei-qing，WANG Shu-guang, et al. Shaking table test on high-rise isolated and non-isolated structures[J]. Journal of Nanjing University of Technology:Natural Science Edition,2013,35(2): 6-10.

[11] 商昊江,祁皑. 高层隔震结构减震机理探讨[J]. 振动与冲击, 2012,31(4): 8-12.

SHANG Hao-jiang, QI Ai. Isolation mechanism of high-rise isolation structure[J]. Journal of Vibration and Shock,2012,31(4): 8-12.

[12] 苏键,温留汉·黑沙,周福霖.隔震层竖向刚度对高层基础隔震结构的影响[J]. 地震工程与工程振动, 2010,30(3): 166-170.

SU Jian, WEN Liu-han·Heisha, ZHOU Fu-lin. Effects of vertical stiffness of isolation layer on high-rise base isolated buildings[J]. Journal of Earthquake Engineering and Engineering Vibration,2010,30(3): 166-170.

[13] 潘东辉,于国友,张德强. 隔震高层结构的悬臂梁模型的地震反应研究[J]. 工程力学, 2012,29(5): 115-121.

PAN Dong-hui, YU Guo-you, ZHANG De-qiang. Earthquake response analysis of cantilever-beam model of isolated high-rise structure[J]. Engineering Mechanics, 2012,29(5): 115-121.

[14] 周坚. 高层建筑结构力学[M].北京: 机械工业出版社, 2006.

[15] 叠层橡胶支座隔震技术规程: CECS 126—2001[S]. 北京:中国标准出版社,2001.

[16] 建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010.

A simplified calculation method for dynamic characteristics of high-rise shear-wall isolated buildings

WANG Xueqing, ZHAO Ming

(College of Civil Engineering and Architecture, Anhui University of Technology, Maanshan 243032, China)

A simplified calculation method was proposed here for the lateral dynamic characteristics of high-rise shear-wall isolated buildings. When performing the uniaxial analysis, the building structure was modeled with the lumped mass method and the first two modes were analyzed with the response spectrum method based on the criterion of modal masses. Periods, modal shapes and damping ratios of the first two modes were calculated using simplified expressions based on the linear stiffness-gravity ratio considering rotation of base isolation. Numerical simulations showed that the simplified method can catch the dynamic characteristics of the first two modes. The explicit formulas for calculating period ratios of high-rise buildings without base isolation to those with base isolation were proposed. The results provided a foundation for the practical designs of high-rise shear-wall isolated buildings.

high-rise shear-wall building; base isolation; linear stiffness-gravity ratio; dynamic characteristics; simplified calculation

安徽省教育厅重点项目(kJ2013A052)

2015-03-06修改稿收到日期：2015-08-04

王学庆 男，博士，讲师，1977年生

TU352

A

10.13465/j.cnki.jvs.2016.15.021