非轴对称结构约束下破片飞散特性的试验和仿真研究

王马法， 卢芳云， 李翔宇， 林玉亮， 黄　洁

(1．中国空气动力研究与发展中心超高速所，四川　绵阳　621000； 2．国防科学技术大学 理学院，长沙　410073)



非轴对称结构约束下破片飞散特性的试验和仿真研究

王马法1,2， 卢芳云2， 李翔宇2， 林玉亮2， 黄洁1

(1．中国空气动力研究与发展中心超高速所，四川绵阳621000； 2．国防科学技术大学 理学院，长沙410073)

为了研究爆炸变形式破片战斗部变形型面与破片飞散特性的关系，对113mm口径的D型结构型面约束下的破片飞散特性进行了试验，并采用LSDYNA软件对内凹、外凸和D型等三种型面约束下破片的飞散特性进行仿真研究，获得了破片的空间分布特性和初速随方位角的分布规律。结果表明，D型结构的破片主要聚焦在目标方向±10°范围内，且偏心起爆的聚焦效果略好于中心起爆；不同起爆方式下目标方向的破片初速相差不大，都是随方位角的增加而降低；不同型面约束下破片飞散偏折角与爆轰波入射角之间近似满足不同斜率的线性关系。最后根据该线性关系特征提出了能够计算不同型面下飞散偏折角随入射角变化的工程计算式。

爆炸力学；爆炸变形式战斗部；D型结构；飞散偏折角

爆炸变形式破片战斗部是一种新型高效毁伤定向战斗部，它是通过起爆目标方向的变形装药使壳体产生凹陷，再起爆主装药驱动破片更多地飞向目标，实现高效毁伤的[1-3]。其中变形装药驱动壳体凹陷产生的变形型面是破片飞散特性的关键影响因素。国内外已经有许多学者对如何获取变形型面做了大量研究[4-5]，对于变形型面与破片飞散特性的关系也有一些研究[6-8]，这些研究大都利用真实变形后的型面结构来做实验，由于真实型面的结构参数很难准确获取，因此难以得到破片飞散偏折角与爆轰波入射角的关系。

为了研究变形型面与破片飞散特性的关系，通常将变形后的型面近似为圆弧段或直线段。近似为直线段型面的壳体截面与字母“D”相近，因此又称为D型结构。由于D型结构较为简单、易于理论分析，且具有较好的破片聚焦性能、相对容易生产加工等特点，本文对其进行试验研究，并利用LS_DYNA对内凹圆弧型、D型和外凸圆弧型结构的作用过程进行仿真分析，获得其破片速度分布特性和空间分布特性。利用仿真分析可跟踪破片轨迹的优势，获得了不同型面下破片飞散偏折角与爆轰波入射角的关系，最终提出了能够用于计算所有型面下破片飞散偏折角与入射角关系的工程计算式，为爆炸变形式破片战斗部的破片飞散聚焦特性的研究提供了参考。

1　D型结构破片飞散特性试验

1.1试验装置

试验装置直径为113 mm，高200 mm，总重4.2 kg，由装药、内壳层、外壳层、钢珠层和上下端盖组成，如图1所示。其中装药为180 mm高的TNT药柱，轴心到弦线的距离为25 mm，对应的圆心角为120°，药柱重1.66 kg。内壳体厚1 mm，高180 mm。外壳体厚1 mm，高200 mm。钢珠破片层由约4 340枚4 mm钢珠组成。

1.装药　2.内壳体　3.钢珠层　4.外壳体　5.端盖图1　D型结构试验装置结构图Fig.1 Experiment sets of D outline structures

1.2起爆方式及靶板布置

从结构端面起爆，共两发试验装置，起爆点设置如图2所示。将弦线中心位置定义为0°，弧线中心位置定义为180°，如图2所示。试验中分别在0°、90°、135°和180°四个位置处布置彩钢板，测量破片的空间分布。靶板和装置的距离为3.5 m。

图2　起爆方式示意图Fig.2 Schematic of initiation types

1.3试验结果及其分析

1.3.1破片空间分布特性

图3给出了部分回收的靶板，可以看到聚焦区域的靶板破坏较为严重，其余部位的穿孔较为稀疏，由于穿孔直径仅为5 mm左右，因此从图中较难分辨。根据靶板上划分的网格，统计出破片沿方位角方向的分布。

图3　回收的靶板Fig.3 Test boards after experiment

将统计结果以各区域的破片数量占统计破片总数的比率形式进行分析，得到破片数沿方位角分布的直方图如图4所示。图中横坐标为方位角，纵坐标为各区域的破片数占统计破片总数的比率。从图中可以看出，在±10°范围内破片数量明显多于90°和180°处的平均值，90°、135°、180°三个方向的破片数量相差不大。偏心起爆下破片分布的直方图中，0°附近的四个区域的破片数明显高于周围其他区域，说明在0°方向上，偏心起爆下破片的聚焦程度要好于中心起爆。

图4　破片沿方位角分布直方图Fig.4 The fragments distribution with azimuth angle

1.3.2破片速度分布特性

试验测得各位置处的破片平均速度如表1所示，由破片在空气中运动的速度衰减公式[9]v=v0e-ζx，可以推导得到破片初速与平均速度的关系式为：

(1)

式中：x为破片飞行的距离，ζ为速度衰减系数。本试验中x=3.5 m，ζ=0.028 4 m，将其代入上式得到各位置处的破片初速，各位置处的破片初速如表1所示。将破片初速随方位角的变化关系如图5所示。可以看到在20°内，中心起爆和偏心起爆的破片初速相差不大。偏心起爆下，破片速度在40°位置处开始迅速上升，之后随方位角增加而减小；中心起爆下则相反，从40°位置处开始，随方位角的增加而缓慢上升。其中，中心起爆下0°位置速度较大的原因可能是圆弧上的爆轰波反射后汇聚到这个方向，加强了这一区域产物的压力。

表1　 破片速度测试结果

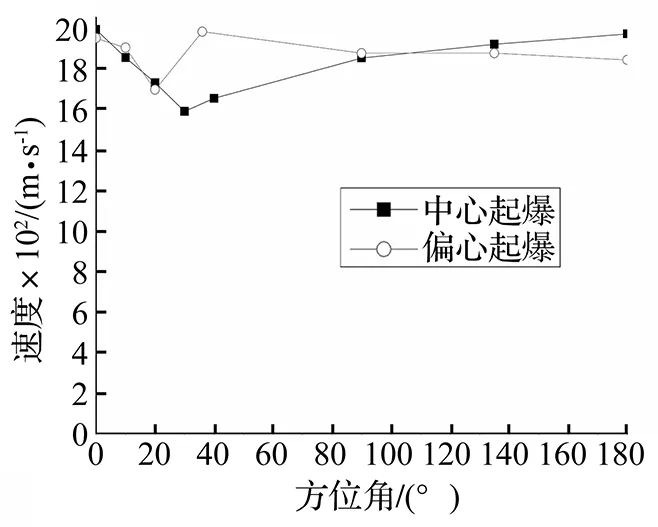
图5　破片初速沿方位角分布图Fig.5 The fragments initial velocities with azimuth angle

2　破片飞散仿真分析及其验证

2.1仿真模型

为了获得D型结构战斗部破片飞散的更多细节特征，本节利用LS-DYNA商用软件对以上战斗部的爆炸过程进行仿真。采用HyperMesh软件对D型结构试验装置进行建模。仿真计算中，采用ALE方法计算炸药与壳体的相互作用，因此需要将D型结构的部件分为Lagrange网格和Euler网格两部分。其中内壳体、外壳体、钢珠和端盖为Lagrange网格；装药、环氧树脂和空气介质为Euler网格，如图6所示。各介质之间采用自动面-面接触，空气网格边界施加压力外流边界条件，以模拟无限欧拉场，避免压力在边界上的反射。考虑到模型的几何对称性，本节仅对1/2模型进行仿真计算。

2.2材料参数

预制破片、端盖、壳体采用随动硬化材料模型来描述预制破片和端盖的动态响应行为，采用流体弹塑性材料模型和Gruneisen状态方程来描述壳体的动态响应行为。表2给出了破片、端盖和壳体的材料参数，表中σs是屈服应力，EY为弹性模量。

名称ρ0/(g·cm-3)EY/Mbarσs/MbarCS1γ0破片、壳体7.852.065.24E-30.3571.921.69端盖2.7850.6892.95E-30.5331.3382.0

TNT装药采用高能炸药燃烧材料模型和标准JWL状态方程来描述装药的爆轰过程。仿真计算中装药的计算参数如表3所示。

表3　TNT装药的JWL状态方程参数

2.3仿真结果与实验结果对比

起爆100 μs后破片飞散空间分布的俯视图如图7所示。可以看到D型结构弦线方向的破片较为集中地飞向了目标方向。

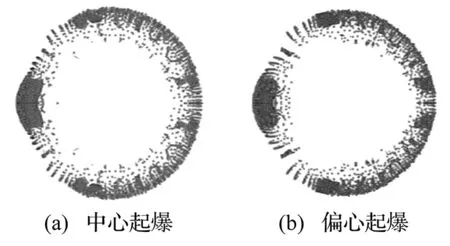
图7　100 μs时刻破片飞散分布图Fig.7 Distribution of fragments at 100 μs

非轴对称型面位置是本文关注的重点，对D型结构弦线位置(目标方向)的破片进行统计，得到其破片在靶板上落点在44°内，因此以44°内的破片总数作为归一化因子对破片数量进行无量纲化，统计结果如图8所示。从直方图的结果可以看出，破片主要集中在0°方向，随着方位角的增加而迅速减少，到30°方位角时，破片数量几乎为0，与试验结果吻合较好。

图8　破片飞散空间分布直方图Fig.8 The bar-maps of fragment distribution

除了对空间分布进行统计外，还对该位置的破片飞散初速进行了统计，获得破片在各方位角上的最大速度曲线如图9所示。对于中心起爆，随着方位角的增加破片初速成先减小后增加的趋势，且在0°位置处破片初速最大，约为2 000 m/s，从图中的对比可以看出，仿真结果与试验结果相吻合。对于偏心起爆，随着方位角的增加破片初速成先迅速减小，再在40°左右突然上升，然后又缓慢减小的趋势，此趋势与试验结果相吻合。在定量比较上虽然与试验数据有些差距，但相差的速度与测得的破片速度相比为小量，因此初速的仿真结果也与试验结果吻合。

图9　破片飞散初速分布Fig.9 The initial velocities distribution of fragments

3　三种型面约束下破片飞散特性

利用以上仿真材料模型和参数对型面为内凹和外凸，型面半径为R0和2R0的非对称结构破片飞散进行了仿真，其中为主体圆柱的半径，起爆方式为偏心起爆。通过对每枚破片进行跟踪，得到其初始位置和在靶板上落点位置的对应关系，并由相应的结构参数计算爆轰波的入射角和破片的飞散偏折角。具体来说，三种结构的计算方法稍有不同，如图10所示。其中，θ1为破片初始位置所在的方位角，θ2为破片初始位置相对于起爆点I的方位角，θ3为破片初始位置和内凹圆弧或者外凸圆弧圆心与对称面所夹的角度，θ4为破片飞散方向与对称面的夹角，α为爆轰波入射方向与该破片处壳体法线的夹角，即入射角，ε为破片飞散方向与壳体法线夹角，即飞散偏折角。

从图上的几何关系可以看出，若将内凹型结构中的θ3定义为负值，则内凹型和外凸型结构破片的入射角α和飞散方位角ε可以由以下公式计算为：

α=θ2-θ3

ε=θ4-θ3

(2)

式中：θ2和θ3可以由破片初始位置、结构参数和起爆点位置确定。由于结构尺寸远小于其与靶板的距离，θ4即可以约等于破片在靶板上落点的方位角。

D型结构的入射角α=θ2，飞散方位角ε=θ4。若将D型结构看作是内凹型和外凸型结构的圆弧半径无穷大，则此时θ3=0，即D型结构的入射角与飞散方位角也可以由式(2)计算。

对仿真结果进行统计，取内凹、外凸或者弦线方向90%的破片进行分析，得到不同结构下飞散偏折角与入射角的关系如图11所示。其中内凹型的型面半径定义为负值。图中可以清楚地看到，对于处在同一初始方位上的破片，其飞散方位角并不完全相同，具有一定的离散性。对于外凸型R=2R0结构，由于起爆点与圆弧圆心距离很近，因此所有破片的爆轰波入射角都非常小。外凸型R=R0结构即为圆柱型结构，其破片飞散方位角随入射角的线性关系不是很明显，飞散方位角接近于0。从内凹型结构和D型结构的结果来看，破片的飞散方位角与入射角近似为线性关系。

图10　破片的飞散角度分析模型Fig.10 Anaysis model of fragments projection angles

图11　破片的飞散方位角统计结果Fig.11 The state results of fragments projection angles

利用Origin软件对结果进行线性拟合，得到线性关系的斜率如表4所示。从表中的拟合度也可以看出，内凹型结构和D型结构的破片飞散角与入射角之间为线性关系，外凸型的线性关系则相对较差。将得到的斜率绘制成随R0/R的变化关系图，如图12所示。可以看到，不同结构下破片飞散偏折角与入射角线性关系的斜率并不相同，随着内凹半径的减小，斜率不断增加，随着外凸半径的减小，斜率不断减小。而且斜率与半径比R0/R的关系近似线性关系，线性关系的斜率为-0.237，截距为0.287，即入射角和飞散偏折角的关系可以表述为(拟合度为96.7%)：

ε=(-0.237R0/R+0.287)α

(3)

图12　拟合直线斜率随半径的变化关系Fig.12 The relationship between slopes of fitting lines with radius

结构R=R0R=2R0D型R=-2R0R=-R0R0/R10.50-0.5-1斜率0.0320.2150.2580.3930.535标准差0.0050.0040.0050.0030.039拟合度/%98.898.291.426.226.1

4　结　论

通过对非轴对称结构的破片飞散特性进行试验和仿真分析，得到的主要结论有：

(1) 对于D型结构，破片在弦线方向±10°范围内破片数量明显多于其它方向，且偏心起爆的聚焦效果要好于中心起爆。

(2) 弦线方向的破片初速随方位角的增加而降低。其它方向上，偏心起爆下，破片速度随方位角增加而减小；中心起爆下，随方位角的增加而缓慢上升。

(3) 不同结构约束下，目标方向的破片飞散偏折角与入射角线性关系的斜率不同，斜率与半径比R0/R的近似线性关系。

[1] König P J, Mostert F J. The results of a deformable warhead technology exercise[C]//20th International Symposium on Ballistics,2002.

[2] 曾新吾, 王志兵, 张震宇,等. 爆炸变形战斗部初探[J]. 兵工学报, 2004, 25(3): 285-288.

ZENG Xin-wu, WANG Zhi-bing, ZHANG Zhen-yu, et al. An investigation on explosive deformable warheads[J]. Acta Armamentarii, 2004, 25(3): 285-288.

[3] Howard W S, Lovelace D E. The development and performance of a large diameter deformable warhead[C].43rd Annual Bomb & Warhead Techincal Meeting,1993: 57-77.

[4] 陈放, 马晓青, 王鹏. 爆炸变形定向战斗部壳体变形分析[J]. 兵工学报, 2004, 25(6): 757-760.

CHEN Fang, MA Xiao-qing, WANG Peng.A study on parameters of deformable directional warhead[J]. ActaArmamentarii, 2004, 25(6): 757-760.

[5] 龚柏林, 卢芳云, 李翔宇. 可变形战斗部弹体变形型面的理论模型[J]. 爆炸与冲击, 2010, 30(1): 65-69.

GONG Bai-lin, LU Fang-yun, LI Xiang-yu. A theoreticalmodel for forecasting deformation shapes of deformable warheads[J]. Explosion and Shock Waves, 2010, 30(1): 65-69.

[6] 陈放, 张函, 马晓青,等. 爆炸变形定向战斗部破片控制研究[J]. 北京理工大学学报, 2009, 29(6): 479-483.

CHEN Fang, ZHANG Han, MA Xiao-qing, et al. A study on the control of fragments from a detonation deformable directional warhead[J]. Transactions of Bejing Institute of Technology, 2009, 29(6): 479-483.

[7] 李翔宇, 卢芳云, 王志兵,等. 可变形定向破片战斗部模型试验和数值模拟研究[J]. 国防科学技术大学学报, 2006, 28(1): 121-124.

LI Xiang-yu, LU Fang-yun, WANG Zhi-bing, et al. A study of simulation and experiment of target-directed deformable warhead model[J]. Journal of National University of Defense Technology, 2006, 28(1): 121-124.

[8] Gong B L, Lu F Y, Li X Y, et al. Study on fragment projection angle of D-Shaped warhead[C]//25th International Symposium on Ballistics,2010: 728-735.

[9] 隋树元, 王树山. 终点效应学[M]. 北京: 国防工业出版社, 2000：87-90.

Tests and simulation for dispersion properties of fragments from asymmetric structures

WANG Mafa1,2, LU Fangyun2, LI Xiangyu2, LIN Yuliang2, HUANG Jie1

(1. China Aerodynamics Research and Development Center, Mianyang 621000, China;2. College of Science, National University of Defense Technology, Changsha 410073, China)

In order to study dispersion properties of fragments from deformable warheads affected by a deformed outline, tests of D-outline structures and simulation of concave, convex and D-outline structures were implemented to analyze dispersion properties of fragments.The results of fragments distribution and initial velocities were obtained from tests and simulation. The simulation results were in good agreement with test data. The results showed that fragments focus on a range of ±10° around the target direction; the focusing effect of fragments from asymmetrical initiation structures is better than that from central initiation ones; the initial velocities decrease with increase in azimuth angle, and they are little different for different initiation types qualitatively and quantitatively; the relations between the projection angle of fragments and the incident angle of shock waves are linear with different slopes for different outline structures; based on the linear relation, an engineering formula is proposed to calculate the projection angle for different outline structures.

mechanics of explosion; deformable warhead; D-outline structure; projection angle

国家自然科学基金资助项目(11202237)

2015-02-25修改稿收到日期：2015-08-04

王马法 男，博士，1986年生

卢芳云 女，教授，博士生导师，1963年生

E-mail：fylu@nudt.edu.cn

O383

A

10.13465/j.cnki.jvs.2016.15.020