典型快速谱峭图算法的研究及应用

马新娜, 杨绍普

(1.石家庄铁道大学 信息科学与技术学院，石家庄　050043; 2. 石家庄铁道大学 机械工程学院，石家庄　050043)



典型快速谱峭图算法的研究及应用

马新娜1, 杨绍普2

(1.石家庄铁道大学 信息科学与技术学院，石家庄050043; 2. 石家庄铁道大学 机械工程学院，石家庄050043)

针对工程实际中状态监测下的具体机械部件在特定运行环境中发生故障的原因及类型具有典型性，在分析快速谱峭图算法的基础上，提出了典型快速谱峭图算法。该算法借鉴快速谱峭图算法分层和选取中心频率的思想，以典型故障的三倍特征频率为带宽，快速定位谱峭度最大的频率区间，并将该算法应用于共振解调技术滤波器参数的确定。为了验证该算法的有效性，在滚动轴承故障诊断试验台上进行了振动测试，采用基于典型快速谱峭图算法的共振解调技术进行故障诊断和类型识别。结果表明，基于典型快速谱峭图算法的共振解调技术能够较好的诊断典型故障，具有一定的工程应用价值。

典型快速谱峭图算法; 故障诊断; 滚动轴承；共振解调

状态监测和故障诊断是机械系统正常运行的基本保障[1]。因此，机械设备的故障特征提取和分析工作具有非常重要的实际意义[2]。尤其是早期故障带来的周期性冲击信号是故障诊断的主要判断依据[3-4]。但是机械运转过程中产生的大量振动噪声，为非平稳故障冲击信号的检测带来困难。由Dwyer提出的谱峭度方法对非平稳信号敏感，能够通过计算不同谱线上的峭度值，检测信号中的瞬态信息，定位谱峭度值最大的频带[5-6]。为了节省计算时间，便于工程应用，Antoni提出了“快速谱峭图”的方法[7-9]。对快速谱峭图的层次细化和选层优化，以及将快速谱峭图算法与共振解调、小波变换以及经验模态等技术相结合的研究非常广泛，并取得了一定的应用效果[10-12]。但是，无法从根本上解决快速谱峭图算法确定的共振频带过宽，特征频率过大问题[13]。文献[14]中提出的Protugram算法预先确定了共振频带的宽度，但是没有考虑中心频率的优化选择问题。

考虑实际机械系统中具体部件常见故障具有代表性，结合快速谱峭图方法中心频率的确定方案，提出了典型快速谱峭图算法。并将典型快速谱峭图算法的结果应用于共振解调带通滤波器中心频率及带宽参数的设置。该方法以典型故障的特征频率为依据确定滤波带宽，借鉴快速谱峭度方法寻找峭度最大的中心频率，即弥补了快速谱峭图方法的带宽过大问题，又保证了算法的快速性。以滚动轴承为检测对象，通过实验方式验证了该算法的有效性。实验结果表明该算法具有一定的工程实用价值。

1　典型快速谱峭图算法

1.1谱峭度

谱峭度(Spectral Kurtosis ，SK)的概念最初由Dwyer提出，其基本思想是通过计算谱线上的峭度值确定信号中的冲击频段。谱峭度弥补了功率谱不能检测和提取出信号中瞬态冲击现象的不足。

定义非平稳信号X(t)的系统激励响应Y(t)为[15]:

(1)

式中，H(t,f)为通过短时傅里叶变换计算得到的振动信号在频率f处的复包络。

(2)

式中，γ(τ)为时间宽度很小的时窗函数。定义Y(t)的四阶谱累积量为：

f≠0

(3)

式中，S(f)为谱瞬时距，表示复包络能量，定义2n阶谱瞬时距S2nY(f)为：

(4)

谱峭度表示概率密度函数的峰值，定义为四阶归一化累积量：

f≠0

(5)

含噪声的故障振动信号Z(t)的谱峭度为：

(6)

式中，KY(f)为不含噪声的故障振动信号Y(t)的谱峭度，ρ(f)为信噪比的倒数。

(7)

式中，SM(f)、SY(f)分别为噪声和故障信号的功率谱密度。信噪比、谱峭度的值取决于所选共振频带。因此谱峭度是中心频率与带宽的函数。故障诊断正确的前提正是寻求能使峭度极大化的共振频带的中心频率和带宽。

1.2快速谱峭图算法

快速谱峭图算法是通过对信号采用频带交替二分法或三分法进行分解，构建树状带通滤波器组实现。以二分法为例，快速谱峭图算法[16-17]的流程如下：

1) 构建一个多通滤波器h0(n)和一个高通滤波器h1(n)：

h0(n)=h(n)ejπn/4

(f∈[0,1/4])

(8)

(9)

式中：h(n)为截止频率1/8的低通滤波器模型。

2) 对滤波后的信号再次进行带通滤波。

3) 重复步骤2)多次，得到快速谱峭图分层结构图如下图1所示。

图1　快速谱峭图分层结构图Fig.1 Structure of fast kurtogram

传统上，从谱峭图谱中找出峭度值最大的频段作为中心频率和带宽的最优组合，进行故障特征分析。但是通过快速谱峭图算法得到的频段往往带宽过大。而且，当算法中分析的层数较多时，所划分的频带区域带宽过小，失去讨论的意义。

1.3典型快速谱峭图算法

虽然故障监测对象种类繁多，但针对具体机械环境中某一类具体部件的状态监测和故障诊断，产生的故障位置和诱因具有相似性。在工程实际中，经过长时间的跟踪和经验总结，往往重点开展常见典型故障的监测工作。

将滚动轴承作为监测对象，在借鉴快速谱峭图中心频率选定方法的基础上，根据频谱中存在三次谐波时对应的峭度值最大原则[18]，取典型故障的三倍故障特征频率为区间带宽，提出了典型快速谱峭图算法。

以某种典型故障为例，假设其故障特征频为f，采样频率为fs。根据典型快速谱峭图算法，所有选取频带的带宽为3f，第0层选取一个频带，其中心频率为(1/4)fs。第1层选取两个频带，其中心频率分别为(1/8)fs和(3/8)fs。以此类推，第i层选取2i个频带。其频带的中心频率可以表示为：

(10)

假设j为从低频到高频所选频带的序号j=1,2,3,…,2i，则式(10)中参数k=2j-1。当层数i较大时，第i层的频带之间会发生重叠。具体分层次数可以根据实际需要确定，但为了保证对采样区间的全覆盖，最大层数i的最小取值要满足fs/2i<3f条件。如果某个频带的边界超出[0，fs/2]范围，将此频带舍弃。得到典型快速谱峭图的分层结构图，见图2。

图2　典型快速谱峭度分层结构图Fig.2 Structure of typical fast kurtogram

通过典型快速谱峭图算法，可以得到所有常见故障的典型快速谱峭图谱，从中选取峭度值最大的频带进行分析。典型快速谱峭图算法的流程见图3。

图3　典型快速谱峭图算法流程图Fig.3 The flow chart of typical fast kurtogram

2　基于典型快速谱峭图算法的共振解调技术

20世纪70年代瑞典SKF公司提出的共振解调技术根据“周期性故障冲击信号激起系统高频共振现象”，通过振动信号频谱图中的共振带进行故障诊断，具有较高的准确率得到了一定应用。为了弥补共振解调技术中带通滤波器中心频率和带宽难于设定的不足[19-20]，将典型快速谱峭图算法应用到共振解调技术中，形成基于典型快速谱峭图算法的共振解调技术。具体流程如图4所示。

图4　基于典型快速谱峭图算法的共振解调方法Fig.4 Demodulated resonance based on typical fast kurtogram

将典型快速谱峭度图算法得到的峭度最大频带的中心频率和带宽作为共振解调带通滤波器的参数。通过共振解调技术找到采集的振动信号中的故障信号和系统中相同频率固有振荡产生的高频共振信息，然后分离故障特征信号，进行频谱分析，判断故障的类型。

3　实例验证

3.1实验环境

为了检验典型快速谱峭图算法的有效性，以60 t级铁路货车352226X2-RZ型轮对滚动轴承为研究对象，采用基于典型快速谱峭图算法的共振解调技术进行故障诊断。所用铁路货车轮对实验台及滚动轴承振动测试实验如图5所示。

图5　铁路货车轮对实验台Fig.5 The experiment platform of railway wheel-set

实验所用轮对滚动轴承存在较严重的外圈剥离故障，故障为长时间安装在铁路货车上运行形成的自然故障，除此之外，轴承表面存在细小划痕损伤。故障轴承的结构参数见表1。

表1　故障轴承的结构参数

根据实验中检测部件所在转轴的转速频率和轴承的结构参数，可以通过计算得到滚动轴承的各部件故障特征频率。实验工况和主要部件的故障特征频率见表2。

表2　实验工况及故障特征频率

实验过程中，采集多组轴承恒定转速下的加速度振动信号，用于检验基于典型快速谱峭图算法的共振解调方法的有效性。选取其中一组振动信号说明实验效果，局部时域信号如图6所示。

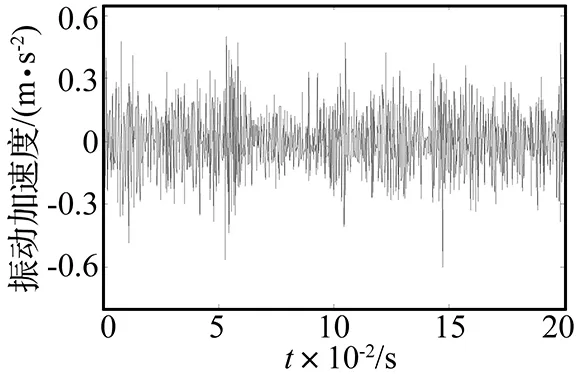
图6　振动信号局部时域图Fig 6 Vibration signal in time domain

3.2故障诊断

为了更好的对比快速谱峭图算法和典型快速谱峭图算法的区别。分别采用基于快速谱峭图算法的共振解调技术和基于典型快速谱峭图算法的共振解调技术进行滚动轴承的故障分析和诊断。

利用快速谱峭图算法，求得快速谱峭图如图7所示。在图中第一层第二个区间的峭度值最大为19.508 2。因此，利用快速谱峭图算法得到的最大峭度区间的中心频率为4 800 Hz，带宽为3 200 Hz。

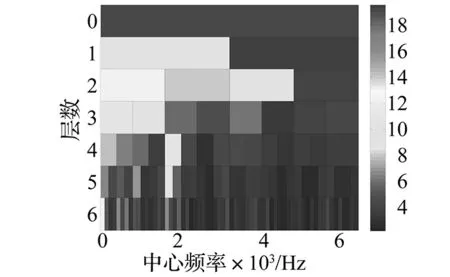
图7　快速峭度图Fig.7 Fast kurtogram

铁路货车轮对滚动轴承的现场典型故障分为外圈、内圈、滚动体三种类型，将此三种故障作为典型故障(为了便于计算对三种故障特征频率分别取整后使用，即68 Hz、89 Hz、28 Hz)。利用典型快速谱峭图算法进行分析，分别得到外圈典型故障、内圈典型故障和滚动体典型故障的典型快速谱峭图，如图8(a)，(b)，(c)所示。

外圈典型故障下求得的典型快速谱峭图(图8(a))的各区间中，第4层第16个区间的峭度最大，峭度值为21.686 1，此区间的中心频率为6 200 Hz，带宽为204 Hz。内圈典型故障下求得的图8(b)的各区间中第6层第63个的峭度值最大，峭度值为19.976 4，此区间的中心频率为6 250 Hz，带宽为267 Hz。滚动体典型故障下求得的图8(c)的各区间中第6层第64个峭度值最大，峭度值为19.987 3，此区间的中心频率为6 350 Hz，带宽为84 Hz。选取其中峭度值最大的区间即图8(a)中的中心频率为6 200 Hz，带宽为204 Hz的区间进行进一步分析。

图8　典型快速谱峭图Fig.8 Typical fast kurtogram

分别将快速谱峭图算法和典型快速谱峭图算法得到的区间中心频率和带宽作为共振解调技术中的带通滤波器的参数进行分析。得到滚动轴承故障频谱分析图，如图9所示。

图9　频谱分析比较Fig.9 Comparison of spectral analysis

从图9(a)中可以看出，利用基于快速谱峭图的共振解调方法可以找到峰值频率68.1 Hz，与计算求得滚动轴承外圈故障特征频率67.53 Hz较接近，可以诊断出滚动轴承存在外圈故障。图9(a)中存在近似的二倍频峰值135.7 Hz和三倍频峰值203.6 Hz。但是故障轴承使用过程中自然形成一些微小划痕，因此频谱图中还出现了较多其它频率的尖峰值，使得二倍频和三倍频峰值淹没其中，不能明显识别出来。

从图9(b)中可以看出，利用基于典型快速谱峭图的共振解调方法可以清晰的找到峰值频率68.1 Hz，136.1 Hz，204.6 Hz，与计算求得滚动轴承外圈故障特征频率67.53Hz，二倍故障特征频率135.06 Hz，三倍故障特征频率202.59 Hz较接近，可以诊断为滚动轴承存在外圈故障。

3.3效果分析

(1) 从上面的故障诊断分析，可以验证基于典型快速谱峭图的共振解调方法能够较好的在实验室环境中识别出铁路货车滚动轴承的故障和故障具体类型。

(2) 相对于快速谱峭图算法，典型快速谱峭图算法应用于共振解调技术时对干扰信号具有更好的抗干扰性，能够更好的进行滚动轴承的故障诊断。

(3) 典型快速谱峭图算法专注于工程实际中典型故障的检测，要求在故障检测方面具有一定的实际先验经验。

4　结　论

本文在分析了快速谱峭图算法基础上，吸取了快速谱峭图中快速定位中心频率的方法，结合工程实际中典型故障诊断的重要性，选取三倍典型故障频率为带宽，提出了典型快速谱峭图算法。为了验证此算法的可行性，在铁路货车轮对振动实验台上进行滚动轴承的故障振动测试。结果表明，将典型快速谱峭图算法与共振解调技术相结合用于滚动轴承的故障诊断，能够较好地诊断出滚动轴承的故障类型，验证了典型快速谱峭图算法的有效性。

[1] 赵志宏, 杨绍普, 李韶华. 基于Hilbert谱奇异值的轴承故障诊断[J]. 中国机械工程，2013，24(3): 346-350.

ZHAO Zhi-hong, YANG Shao-pu, LI Shao-hua. Bear-ing fault diagnosis based on Hilbert spectrum and singular value decomposition[J]. China Mechani-cal Engineering, 2013, 24(3):346-350.

[2] 唐贵基，王晓龙. 基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法[J]. 中国机械工程，2015,26(11)：1450-1456.

TANG Gui-ji, WANG Xiao-long. Diagnosis method for rolling bearing incipient faults based on sparsity of envelope spectrum and maximum correlated kurtosis deconvolution[J]. China Mechanical Engineering, 2015,26(11)：1450-1456.

[3] 陈彬强，张周锁，訾艳阳，等. 机械故障诊断的衍生增强离散解析小波分析框架[J]. 机械工程学报，2014,50(17)：77-86.

CHEN Bing-qiang, ZHANG Zhou-suo, ZI Yang-yang, et al. Novel ensemble analytic discrete framelet expansion for machinery fault diagnosis [J]. Journal of Mechanical Engineering, 2014, 50(17):77-86.

[4] 明安波，褚福磊，张炜. 滚动轴承故障特征提取的频谱自相关方法[J]. 机械工程学报，2012, 48(19)：65-71.

MING An-bo,CHU Fu-lei, ZHANG Wei. Feature extracting method in the rolling element bearing fault diagnosis spectrum auto-correlation[J]. Journal of Mechanical Engineering, 2012, 48(19): 65-71.

[5] Dwyer R F. Detection of non-gaussian signals by frequency domain kurtosis estimation[C]// Acoustic, speech and signal processing.Boston: IEEE inter-national conference on ICASSP, 1983:607-610.

[6] Randall R B, Antoni J. Rolling element bearing diagnosticsa tutorial[J]. Mechanical System and Signal Processing, 2011, 25:485-520.

[7] Antoni N J. The spectral kurtosis: A useful tool for characterizing non-stationary signals[J]. Mechanical System and Signal Processing, 2006, 20(6):282-307.

[8] Antoni J. Randall R B. The spectral kurtosis: Application to the vibration surveillance and diagnostics of rotating machines[J]. Mechanical system and Signal Processing，2006，20(6)：308-331.

[9] Antoni J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 21(1):108-124.

[10] 彭畅，柏林，谢小亮. 基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J]. 振动与冲击，2012,31(20)：143-146.

PENG Chang, BO Lin, XIE Xiao-liang. Fault diagnosis method of rolling element bearings based on EEMD, measure-factor and fast kurtogram[J]. Journal of Vibration and Shock, 2012,31(20)：143-146 .

[11] 林京. 连续小波变换及其在滚动轴承故障诊断中的应用[J]. 西安交通大学学报，1999，33(11)：108-110.

LIN Jing. Continuous wavelet transform and its application for bearing diagnosis[J]. Journal of Xi’an Jiaotong University, 1999,33(11):108-110.

[12] Wang Yan-xue, Liang Ming. An adaptive SK technique and its application for fault detection of rolling element bearings[J]. Mechanical Systems and Signal Processing，2011,25(1):1750-1764.

[13] 代士超，郭瑜，伍星，等. 基于子频带谱峭度平均的快速谱峭度图算法改进[J]. 振动与冲击，2015, 34(7)：98-102.

DAI Shi-chao, GUO Yu, WU Xing, et al. Improvement on fast kurtogram algorithm based on sub-frequency-band spectral kurtosis average[J].Journal of Vibration and Shock, 2015, 34(7)：98-102.

[14] Barszcz T，Jabionski A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the kurtogram[J]. Mechanical Systems and Signal Processing，2011，25(1)：431-451.

[15] 蔡艳平，李艾华，石林锁，等. 基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击，2011,30(2)：167-191.

CAI Yan-ping, LI Ai-hua, SHI Lin-suo, et al. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock, 2011,30(2)：167-191.

[16] 张晓涛，唐力伟，王平，等. 基于SVD与Fast kurtogram算法的滚动轴承声发射故障诊断[J]. 振动与冲击，2014,33(10)：101-105.

ZHANG Xiao-tao, TANG Li-wei, WANG Ping, et al. Acoustic emission fault diagnosis of rolling bearing based SVD and Fast kurtogramalgorithm[J]. Journal of Vibration and Shock, 2014, 33(10): 101-105.

[17] 王宏超，陈进，董广明，等. 基于快速kurtogram算法的共振解调方法在滚动轴承故障特征提取中的应用[J]. 振动与冲击，2013, 32(1)：35-37.

WANG Hong-chao, CHEN Jin, DONG Guang-ming, et al. Application of resonance demodulation in rolling bearing fault feature extraction based on fast computation of kurtogram[J].Journal of Vibration and Shock, 2013, 32(1): 35-37.

[18] 丁康，黄志东，林慧斌. 一种谱峭度和Morlet小波的滚动轴承微弱故障诊断方法[J]. 振动工程学报，2014,27(1)： 128-135.

DING Kang, HUANG Zhi-dong, LIN Hui-bin.A weak fault diagnosis method for rolling element bearings based on Morlet wavelet and spectral kurtosis[J]. Journal of Vibration Engineering, 2014, 27(1): 128-135.

[19] 张晓涛，唐力伟，王平，等. 轴承故障声发射信号多频带共振解调方法[J]. 振动、测试与诊断，2015,35(2)：363-368.

ZHANG Xiao-tao, TANG Li-wei, WANG Ping, et al. Multi-band resonance demodulation of rolling bearing fault acoustic emission signal[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(2): 363-368.

[20] 张龙，熊国良，黄文艺. 复小波共振解调频带优化方法和新指标[J]，机械工程学报，2015，51(3)：129-138.

ZHANG Long, XIONG Guo-liang, HUANG Wen-yi. New procedure and index for the parameter optimization of complex wavelet based resonance demodulation [J]. Journal of Mechanical Engineering, 2015, 51(3): 129-138.

Typical fast kurtogram algorithm and its application

MA Xinna1, YANG Shaopu2

(1. School of Information Science and Technology, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2. College of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

In practical engineering, the causes and types of occurring faults on specific mechanical components are typical. On the basis of analyzing fast kurtograms, the typical fast kurtogram algorithm was presented here. With the fast kurtogram ideas of hierarchy and selecting central frequency, three times of characteristic frequencies of typical faults were taken as a bandwidth to quickly find the frequency interval of the maximum spectral kurtosis. This algorithm was used to automatically determine filter’s parameters for resonance demodulation technique. In order to verify the validity of this algorithm, vibration tests were conducted on a rolling bearing fault diagnosis test platform. The fault diagnosis and type recognition were implemented using the reonance dempdulation technique based on the typical fast kurtogram alororithm. The results demonstrated that the proposed algorithm is reliable and can meet the requirements of engineering application.

typical fast kurtogram; fault diagnosis; rolling bearing; resonance demodulation

国家自然基金项目(11372197；11227201)；河北省自然基金项目(E2014210078)

2015-11-09修改稿收到日期：2016-01-28

马新娜 女，博士，副教授，1978年生

TH133.33;TP391.9

A

10.13465/j.cnki.jvs.2016.15.018