平行双自由面岩体爆破炮孔堵塞效应研究

王　洋， 史秀志， 苟永刚， 郭　霆

(中南大学 资源与安全工程学院，长沙　410083)



平行双自由面岩体爆破炮孔堵塞效应研究

王洋， 史秀志， 苟永刚， 郭霆

(中南大学 资源与安全工程学院，长沙410083)

为研究平行双自由面岩体炮孔堵塞效应，借助动量定理推导出炮孔堵塞长度范围计算公式；利用有限元软件LS-DYNA，采用ALE多物质算法，建立4 m深的四孔无限岩体模型。通过分析自由面附近单元应力峰值和岩体应力分布规律，得到：炸药长度为2.4 m的无堵塞炮孔爆破效果最优；1.2 m炸药长度的炮孔模型中，单向堵塞和非对称堵塞爆破对岩体的应力分布规律无影响，但岩体自由面附近单元的应力峰值增大，作用时间加长；双向对称堵塞的最佳堵塞长度为1.0～1.2 m。对比不同参数下的工程爆破效果，采用数值模拟结果的工程爆效最优，证明了数值模拟结果的正确性。

平行双自由面；岩体爆破；堵塞长度；数值模拟

自由面在爆破中起重要作用，自由面数目越多, 爆破效果越好, 耗药量也越少[1]。目前，关于岩体炮孔堵塞的研究有很多[2-6]，其中平行双自由面岩体爆破堵塞的研究较少：刘博[7]利用水泥砂浆模型爆破实验模拟地下矿山拉槽爆破，得出炮孔堵塞的最佳水炮泥长度；刘冰川[8]通过数值模拟手段，得出一次成井爆破的最优堵塞长度；李廷春[9]借助动量定理推导出一次成井堵塞长度的上、下限计算公式。然而，对于平行双自由面岩体爆破堵塞研究，仍需要对以下三个方面进行完善：最小抵抗线长度与堵塞长度不相等的岩体炮孔最优堵塞长度的理论计算值；双自由面岩体爆破堵塞需要充分考虑炮孔无堵塞、单向堵塞和双向堵塞三种堵塞条件；实际工程需要考虑多孔装药的群药包作用，需要对不同堵塞条件下的多孔爆破效应作分析对比试验。

本文利用动量定理推导出平行双自由面岩体的炮孔堵塞长度；借助有限元软件对不同方式下的炮孔堵塞爆破作数值模拟实验研究。分析炮孔无堵塞、单向堵塞和双向堵塞的岩体应力分布规律，得到平行双自由面岩体爆破的最优堵塞参数，为地下矿山采场破顶爆破、一次成井等爆破工程堵塞参数优选提供指导。

1　炮孔堵塞长度范围理论计算

理论计算封堵长度时，需作如下假设：爆轰气体为理想气体，爆生气体瞬间充满炮孔，并作用于炮孔空间各个部位和方向；封堵物的整体运动过程按近似刚体运动进行分析；堵塞物冲出槽腔的时间极短，堵塞物获得初始速度后做匀速运动。

1.1堵塞物冲出炮孔所需时间

爆生气体的瞬时压力P为：

(1)

式中：ρe为装药密度，kg/m3；dc和db分别为装药直径和掏槽孔直径，mm；De为爆轰速度，m/s；γ为爆生气体的多方指数，在爆炸作用初期，当爆生气体压力大于临界压力PH，γ=3 ；当爆生气体压力小于临界压力PH，γ=1.3～1.5。

封堵物初始运动时，爆生气体在封堵物端部产生的初始冲量IB为：

(2)

式中：ls为炮孔封堵长度最小值，m；Cs为堵塞物中的弹性波速度，m/s。封堵物与孔壁的摩擦力产生的初始冲量If，封堵物初始运动时，假设封堵物与孔壁的摩擦系数为f。

封堵物与孔壁的摩擦力产生的初始冲量If1为：

(3)

(4)

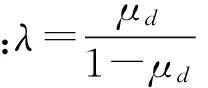
根据冲量定理，初速度V0可表示为：

IB-If±IG=MV0

(5)

即：

(6)

炮孔内堵塞物冲出炮孔所用时间t为：

(7)

对于上端封堵，封堵物初始运动时，封堵物自身重力为阻力，上式中正负号取负号；对于下端封堵，封堵物自身重力为动力，上式中正负号取正号。

1.2炮孔最小堵塞长度确定

炮孔最短封堵长度的确定原则是：封堵物排出前，槽腔范围内岩石破碎完成[7]。根据爆炸力学和应力波理论可知，介质破碎所需要的时间td1为：

(8)

式中：W为装药的最小抵抗线，m；CP和CR分别为被爆介质中的纵波速度和表面锐利波速度，m/s。 根据上述炮孔最短封堵长度确定原则可得t=td1，即：

(9)

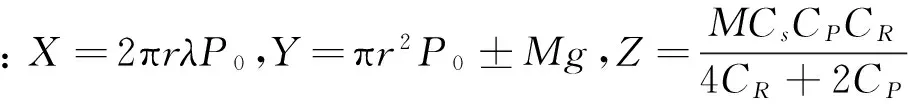
1.3炮孔最大堵塞长度确定

炮孔最长封堵长度的确定原则是：保证封堵物在爆破漏斗周边裂隙形成之前排出槽腔[9-10]。爆破漏斗初始形成的时间td2为：

(10)

式中：W为最小抵抗线,m，lh为封堵长度的最大值，m；α为破碎角，(°)；C1为裂隙扩展平均速度，m/s，C1=0.1CP。

根据上述炮孔上、下端最长封堵长度确定原则可得：

(11)

式中：X=CPC1MCScos(α/2),Y=2k(2C1cos(α/2)+CP)(πr2P0±Mg),Z=4krfλP(2C1cos(α/2)+CP)

根据炮孔中堵塞物重力冲量的方向决定式中重力的正负号。

由于敞口模型中爆生气体压力泄压迅速，故该计算公式只适用于双向堵塞炮孔。值得注意的是，由于该计算过程中有很多参数简化，利用式(9)和(11)得到的炮孔堵塞长度范围较宽，需要充分结合有限元数值模拟结果确定最优爆破堵塞长度。

2　炮孔堵塞长度的数值模拟研究

2.1建立数值计算模型

2.1.1模型几何尺寸

模型以工程实例为基础，简化工程爆破参数，建立标准的数值计算模型并计算得到结果。模型长、宽为4.0 m，高4.0 m，在模型中心布置四个炮孔，炮孔布置的网格参数为1 m×1 m，炮孔直径为0.016 m，径向耦合装药。根据问题的对称性取模型的1/4进行建模，计算模型如图1所示，模型堵塞长度分为顶部堵塞长度(L1)和底部堵塞长度(L2)两部分。模型的侧面设为透射边界即模拟无限岩体；对称平面上施加对称边界条件；上表面、下表面为自然边界条件即模拟岩体的上下自由面[10]。

图1　岩体爆破数值计算模型Fig.1 Numerical calculation model of rock blasting

2.1.2材料参数

模型中炸药参数采用矿山爆破中使用的二号岩石乳化炸药，其状态方程为：

(12)

式中：P为由JWL 状态方程决定的压力；A、B、R1、R2、ω均为与炸药相关的材料常数；V为相对体积；E0为初始比内能。其各参数值见表1。

表1　乳化炸药材料参数及JWL状态方程参数

本文爆破模拟过程包含矿体和河砂两种被爆物，矿体(选取的铅锌地下矿山主要是灰岩和砂页岩)选用

塑性动力学模型(MAT_PLASTIC_KINEMATIC)；河砂的特性类似于土壤(砂土)，选用土壤和泡沫模型(MAT_SOIL_AND_FOAM)来模拟。

由于炸药爆炸时附近岩体应变很大，应变率效应明显，爆炸荷载作用下的岩体模型采用包含应变率效应的塑性硬化模型[10]：

(13)

表2　矿体塑性动力学模型材料参数

注：该模型共需9个参数，上表仅给出8个，另外一个为失效应变，这里暂不考虑其影响。

2.1.3最优炮孔堵塞判定依据

Vutukuri 等[11]指出，最优的爆破方案满足以下条件：① 堵塞区的岩石应部分破碎而不产生大量大块；② 当A(或D)上记录单元的最大有效应力不大于花岗岩的动态抗拉强度和B(或C)上记录单元的最大有效应力不小于花岗岩的动态抗拉强度时，堵塞区的岩体只产生破裂而不会产生大量飞石。模型中岩体的动态抗拉强度为10 MPa，分别选取上、下端孔口附近时间历程记录面A(距顶端孔口0.2 m)、B(距顶端孔口0.4 m)、C(距底端孔口0.4 m)、D(距底端孔口0.2 m)，各记录面位置如图1。

表3　河砂材料模型的计算参数

常规炸药引起的粉碎区半径r1为装药半径的3倍～5倍，破碎区半径r2为装药半径的10倍～15倍[12-14]。忽略炮孔间的相互影响，则模型中每个炮孔起爆均类似于柱状炸药在半无限介质中起爆，所以群孔起爆时的等效弹性边界为各孔各自形成的破碎区的包络线[15]。由于药包的共同作用会使得炮孔中间部分的岩体应力值远大于炮孔外围岩体的应力值，故选取时间历程面上单元应力峰值时应避开该区域单元。通过对比时程记录面上单元应力峰值与岩石动态抗拉强度值，可得出不同堵塞下的岩体爆破效果。

2.2结果分析

2.2.1无堵塞炮孔模型爆破的药包长度效应

模型中炮孔直径是定值，爆破装药长度的变化即为爆破单耗的变化。现分别模拟1.2 m, 1.8 m, 2.4 m, 3.0 m, 3.6 m长度的炸药在模型中的爆破效应，炸药中心置于炮孔中心位置，炮孔无堵塞，采用中心起爆。

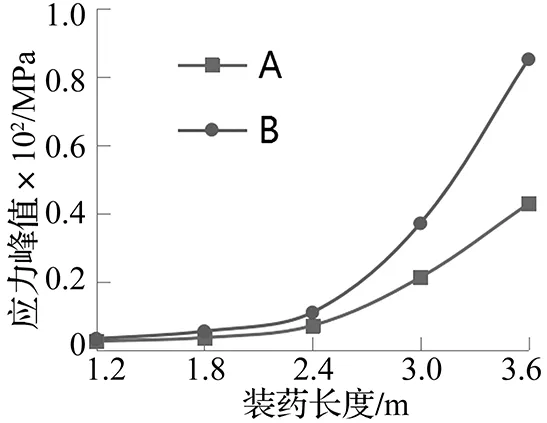
图2　模型A、B面上各记录点的最大有效应力与堵塞长度关系曲线Fig.2 Model A and B each record point on the surface of the maximum effective stress and the block length relation curve

经模拟计算，不同炸药长度爆破模型的时间记录面A、B上各记录单元的最大有效应力与炸药长度的关系曲线如图2所示。当装药长度为3.0 m 时，A上各记录点最大有效应力为21.3 MPa，大于岩石的动态抗拉强度，当装药长度为2.4 m时，A上各记录点最大有效应力为7.16 MPa，小于岩石的最大有效应力；当装药长度为2.4 m 时，B上各记录点最大有效应力为11.04 MPa，大于岩石的动态抗拉强度，当装药长度为1.8 m 时，B上各记录点上最大有效应力为5.53 MPa，小于岩石的动态抗拉强度。在本次模拟实验不堵塞双自由面岩体中装药长度为2.4 m的岩体中爆破只产生破裂而不会有大量飞石，即2.4～3m 装药长度的不堵塞炮孔岩体爆破效果最佳。

2.2.2炮孔不同堵塞方式下的模型应力分布规律

模型采用1.2 m中心装药长度，建立无堵塞炮孔模型、单向堵塞炮孔模型(L1=1.2 m;L2=0.0 m)、双向非对称堵塞(L1=1.2 m;L2=0.2 m)和双向对称堵塞(L1=L2=1.2 m)。各种工况在起爆后0.4 ms时的应力分布如图3、图4所示。

表4　节点有效应力极大值表

图3　t=0.4 ms, 不同堵塞条件下模型的应力图Fig.3 t=0.4 ms, stress diagram under different conditions Model blockage

图4　t=0.4 ms, 不同堵塞条件下模型中心剖面应力分布图Fig.4 t=0.4 ms, model under the conditions of different plugging center section stress distribution

图3和图4表明，四种堵塞条件下多孔爆破的平行双自由面岩体应力分布规律相近，炮孔中心区域的应力明显高于其附近的应力，这与应力波干涉理论相吻合，而炮孔壁处压力又明显高于其附近位置压力，而且出现时间较早，且持续时间较长，这有力地支持了爆炸应力波与高压气体联合作用理论。通过分析A、B、C、D面上单元有效应力峰值得，炮孔单向堵塞增加了堵塞端爆破应力的作用时间，但是由于卸压较快，岩体单元的压力峰值并不高；双向堵塞时堵塞物长度对岩体自由面附近监测单元的应力峰值影响较大，爆生气体对岩体的应力作用时间最长，岩体特征单元的应力峰值最大，故工程爆破中最优的堵塞方式为双向对称堵塞。

2.2.3岩体爆破炮孔双向对称堵塞的最优堵塞长度

炮孔堵塞对爆破的初始压力影响较小，炮孔中双向堵塞的堵塞物增加爆轰气体在炮孔内的作用时间，使得炮孔内的堵塞物压缩变形，从而改变堵塞物的体积分数分布规律。图5为不同长度的堵塞物在1 ms时体积分数分布图，堵塞物上部密度随堵塞长度的增加变化较小，当堵塞长度为0.8～1.4 m 时，堵塞物的上部体积分数基本相同；0.8～1.4 m堵塞物底端体积分数变化相近，但是随着爆生气体的作用时间延长，较短且变形较大的堵塞物会率先冲出炮孔，即炮孔堵塞长度越大，爆轰气体从炮孔冲出，增加爆破的能量利用率。

图5　t=1 ms时不同长度的堵塞物的体积分数分布图Fig.5 t=1 ms different lengths of blockage volume fraction distribution

由图6可知，在炮孔双向堵塞中，当堵塞长度为0～1.0 m时，A、B上各记录点最大有效应力都小于岩石动态抗拉强度；堵塞长度为1.2～1.4 m时，A、B上各记录点最大有效应力都大于岩石的动态抗拉强度；堵塞长度为1.0～1.2 m时，A上记录点最大有效应力小于岩石的动态抗拉强度，B上各记录点最大有效应力大于圆岩石的动态抗拉强度。即堵塞长度为1.0～1.2 m时，爆破两端产生破裂而没有大量飞石。图7表明，监测点的质点振动速度随堵塞长度的增大而增大，堵塞长度从0.8 m增加到1.2 m阶段振动速度增加迅速，这说明堵塞作用干预了炸药能量的释放方式，堵塞物长度由0.8 m增加到1.2 m的过程，削弱了空气冲击波的比例，增加了传向周围岩体的能量。

综上分析可得，平行双自由面岩体炮孔对称堵塞的最佳堵塞长度为1.0～1.2 m。

图6　模型A、B面上各记录点的最大有效应力与堵塞长度关系曲线Fig.6 The relation curves between the maximum effective stress of all elements on surface A、B and stemming length

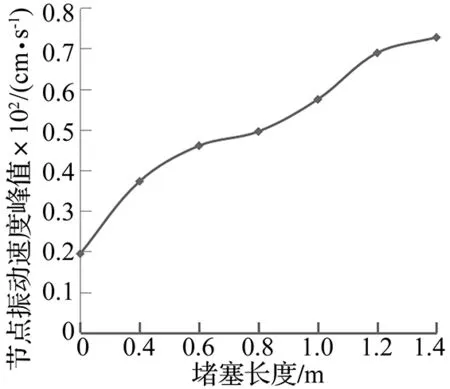
图7　距模型中心2.0 m处爆破震动速度峰值与堵塞长度关系曲线。Fig.7 The relation curves between the vibration velocity of all nodes 2.0m distances from the center of the model and stemming length vibration velocity

3　工程实例

图8为某地下矿山S2#N VCR实验采场装药列剖面示意图，采场岩石主要为黄铁铅锌矿，岩体裂隙较多，围岩较复杂。采场总破顶高度约9 m，拉槽区炮孔直径为0.16 m，每层装药高度H=1.2 m，堵塞物为河沙，采用药包中心起爆。采场利用孔内微差技术分层爆破，破顶层高度3.8 m。

利用式(9)、 (11)计算堵塞物长度的上、下限，数值计算结果为：ls=0.85 m，lh=1.51 m；数值模拟的最优堵塞长度为1.0～1.2 m。由于采场岩体的节理较复杂，故实际应用中堵塞长度值应稍大于分析结果，即采场破顶层上、下端堵塞长度L=1.2 m。为了验证计算结果，分别对比采场岩体结构类似但不同装药高度和堵塞高度的N2#S VCR破顶采场和S5#N VCR破顶采场，三个破顶采场的爆破效果对比结果见表5。

图8　采场破顶爆破装药示意图Fig.8 Stope roof blasting charge schematic diagram

工程效果S2#NVCR采场N2#SVCR采场S5#NVCR采场H=1.2m;L=1.2mH=2.0m;L=1.2mH=1.2m;L=1.5m爆堆表层块度块度均匀,无大块无大块有大块采场破顶区顶板无明显破损较烂,有松石无明显破损破顶层爆破单耗/(kg·t-1)0.240.290.21

4　结　论

(1) 基于堵塞物在炮孔中的运动规律和平行双自由面岩体的爆破破岩机理，借助动量定理，推导出平行双自由面岩体炮孔双向堵塞方式下的堵塞长度计算公式。

(2) 将平行双自由面岩体炮孔堵塞分为无堵塞、单向堵塞和双向堵塞三种堵塞方式，借助数值模拟软件，应用有效应力峰值分析法得出：未堵塞炮孔中2.4～3.0 m装药长度的爆破效果最佳；单向堵塞炮孔和非对称双向堵塞方式减小了爆炸对岩体的应力作用，但对岩体的群药包爆破应力分布规律无影响；双向对称堵塞的最优堵塞长度数值模拟分析值为1.0～1.2 m。

(3) 选取三个实验采场，对比H=1.2 m；L=1.2 m、H=2.0 m；L=1.2 m和H=1.2 m；L=1.5 m的破顶爆破，使用H=1.2 m；L=1.2 m参数的破顶层爆破单耗低、块度均匀、采场破顶区顶板完整，验证了平行双自由面堵塞长度的计算与数值模拟综合分析结果的正确性。在实际工程中，由于岩体节理的复杂性，选择合理的堵塞长度还应充分考虑岩体的节理分布规律。

[1] 李夕兵，凿岩爆破工程[M]. 长沙：中南大学出版社，2011.

[2] 郝亚飞，李海波，刘恺德，等. 单自由面爆破振动特征的炮孔堵塞长度效应[J].岩土力学，2011， 32(10)：3105-3110.

HAO Ya-fei, LI Hai-bo, LIU Kai-de, et al. Blasthole stemming length effects of single free-face blasting vibration characteristic[J]. Rock and Soil Mechanics, 2011, 32(10): 3105-3110.

[3] 喻长智，古德生，杜炜平，等. 炮孔堵塞长度的计算[J]. 矿冶工程，1999，19(4)：4-11.

YU Chang-zhi, GU De-sheng, DU Wei-ping, et al. A calculation of stem length of blasting hole[J].Mining and Metallurgical Engineering, 1999, 19(4): 4-11.

[4] 罗勇，沈兆武. 炮孔合理堵塞长度的研究[J]. 岩土工程技术，2006， 20(1)：25-28.

LUO Yong, SHEN Zhao-wu. Study on stemming length in hole-charged blasting [J]. Geotechnical Engineering Technique, 2006, 20(1):25-28.

[5] 赵新涛，程贵海，冯国建. 炮孔堵塞长度的计算与实验研究[J].力学季刊, 2010, 31(2): 165-171.

ZHAO Xin-tao, CHENG Gui-hai, FENG Guo-jian. Calculation and experimental study of blast-hole stemming length[J].Chinese Quarterly of Mechanics, 2010, 31(2): 165-171.

[6] 罗伟，朱传云，祝启虎. 隧洞光面爆破中炮孔堵塞长度的数值分析[J]. 岩土力学，2008，29(9): 2487-2491.

LUO Wei, ZHU Chuan-yun, ZHU Qi-hu. Numerical simulation of stemming length in tunnel smooth blasting[J]. Rock and Soil Mechanics, 2008, 29(9): 2487-2491.

[7] 刘博. 水炮泥堵塞作用机理模型试验及应用研究[D]. 长沙：中南大学，2014.

[8] 刘冰川. 深孔爆破一次成井炮孔堵塞理论研究及应用[D]. 长沙：中南大学，2014.

[9] 李廷春，刘洪强. 一次成井掏槽爆破炮孔合理封堵长度研究[J]. 中国矿业大学学报，2012，41(3)：384-389.

LI Ting-chun, LIU Hong-qiang. Optimized cut hole stemming length for shaft excavation using one-step deep-hole blasting[J]. Journal of China University of Mining & Technology, 2012, 41(3)：384-389.

[10] 白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京:科学出版社，2005.

[11] Vutukuri V S, Lama R D. Handbook on mechanical properties of rocks: testing techniques and results[M]. Ohio: Trans Tech. Publications, 1974.

[12] 王明洋，邓宏见，钱七虎. 岩石中侵彻与爆炸作用的近区问题研究[J]. 岩石力学与工程学报，2005，24(16)：2859-2863.

WANG Ming-yang, DENG Hong-jian, QIAN Qi-hu. Study on problems of near cavity of penetration and explosion in rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2859-2863.

[13] Xahykae B A H. 矿岩爆破物理过程[M]. 刘殿中. 北京：冶金工业出版社，1980.

[14] Esena S, Onederraa I, Bilgin H A. Modelling the size of the crushed zone around a blasthole[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(4): 485-495.

[15] 杨建华，卢文波，陈明，等. 岩石爆破开挖诱发振动的等效模拟方法[J]. 爆炸与冲击,2012, 32(2): 157-162.

YANG Jian-hua, LU Wen-bo, CHEN Ming et al. An equivalent simulation method for blasting vibration of surrounding rock[J]. Explosion and Shock Waves,2012,32(2):157-162.

Blast hole stemming length effects of rock blasting with parallel double-free-surface

WANG Yang, SHI Xiuzhi, GOU Yonggang, GUO Ting

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Rock fragmentation was examined for determining how stemming length affected blast effect. The formula for calculating borehole stemming length range was deduced with the momentum theorem. The tests for rock blasting with parallel double-free-surface were simulated with the finite element software ANSYS/LS-DYNA where the multi-material ALE method was used. A four-meter deep and four-hole infinite rock mass model was established. After analyzing the peak stress of the element nearby the free surface and the stress distribution of the rock, it was shown that the optimal explosive length is 2.4 m in a borehole model test without stemming; in the borehole model with one-sided stemming or asymmetric double-sided stemming, blasting has no effect on the stress distribution law of rock mass, but the peak stress of the element near the free surface increases and the acting time is lengthened; the optimal stemming length of the model with symmetric double-sided blast hole is 1.0～1.2 m; the blasting effects of numerical simulation results is the best compared with engineering blast effects with different parmeters, the correctness of numerical simulation results is verified.

parallel double-free-surface; rock mass blasting; stemming length; numerical simulation

国家科技支撑计划项目(2013BAB02B05)

2015-06-05修改稿收到日期：2015-08-05

王洋 男，硕士生，1991年11月生

史秀志 男，教授,博士生导师，1966年1月生

TD235

A

10.13465/j.cnki.jvs.2016.15.013