一种新的相关机械振源盲分离方法

于　刚, 周以齐， 张卫芬

(1.山东大学 高效洁净机械制造教育部重点实验室，济南　250061；2.解放军72850部队，济南　250032)



一种新的相关机械振源盲分离方法

于刚, 周以齐1， 张卫芬2

(1.山东大学 高效洁净机械制造教育部重点实验室，济南250061；2.解放军72850部队，济南250032)

针对传统盲源分离算法在机械振源不满足统计独立特性时，无法有效分离出振源信号的问题，提出了基于信号稀疏特性的相关机械源盲分离方法。盲源分离算法的关键在于准确地估计出混合矩阵。因此，首先提出了不相关源混合矩阵的估计方法；然后针对相关源，提出了有效剔除相关成分的方法，使得剩余信号可以按照不相关源进行处理。通过理论分析、仿真验证以及实测数据分析，验证了该方法的有效性。

盲源分离；振动源；相关源

机械设备运行中，多个部件都会产生一定的振动，导致测量信号通常是多个振源信号的混合。如果能针对每个振源单独地分析其信号特征，对于监测设备运行状态、分析结构特性、控制振动传递等应用具有一定的指导意义。盲源分离(Blind Source Separation, BSS)方法仅依靠测量信号即可得到各源信号及其混合模型，在理论上为振动分析提供了有力的技术手段[1]。独立分量分析(ICA)，利用信号间的统计独立特性，估计出分离矩阵，并用于源信号的分解，在故障诊断[2-3]、模态分析[4-5]等领域均得到了广泛的应用。

而工程应用中，各机械振源之间往往会存在交叉频率成分，导致无法满足ICA算法的独立性假设，从而造成算法失效。周晓峰提出利用小波包分解剔除观测信号间的相关成分，利用剩余分量重构信号进行矩阵估计，成功分离出了多个相关源信号[6]。该方法需要选择合适的小波包分解层数以及设定子带间的互信息阈值，需要较多的人工干预，一定程度上降低了其实用性。孟宗利用类似的思想提取源信号，将经验模态分解应用于测量信号分解，并根据互信息准则重构相关源信号[7]。本文利用源信号在时频域中的稀疏性估计混合矩阵，并提出了一种能有效剔除相关成分的方法，从而形成了一套完整的相关源盲分离算法。

1　BSS基本概念

盲源分离是指输入信号与系统参数均未知的情况下，仅依靠输出测量信号来估计这两项参数。源的混合模型可以表示为：

X(t)=AS(t)+n(t)

(1)

式中：X(t)为N维观测信号，S(t)为M个未知的相互统计独立的输入信号，A为N×M未知的满秩混合矩阵，通常N=M，n(t)为噪声信号。盲源分离的目的是根据独立性测度函数，寻求分离矩阵W，使得W=A-1，利用式(2)使得恢复出来的源信号Y(t)尽可能独立：

Y(t)=WX(t)

(2)

从式(2)可以看出，源分离的关键在于准确地估计出混合矩阵。由于相关源信号不满足统计独立假设，因而无法利用独立性准则有效地估计混合矩阵。本文先以不相关源为例说明矩阵估计的具体过程，然后提出一种有效剔除相关成分的方法，并将两者结合，提出一种新的相关源分离算法。

2　稀疏分量分析

信号稀疏性是指信号在时频域中大多数的时频点取值为零，或者接近于零，但有少数时频点取值明显大于零。当信号具有较好的稀疏性时，观测信号在某一时频点只有一个源的可能性增大。对于隶属同一源信号的时频点将会正比于源信号在测量信号中的混合衰减系数，因此信号的稀疏特性可以被用于估计源信号的混合矩阵。

m个通道信号中包含n个源的模型可表示为：

(3)

xj(t)代表第j个观测信号，aij为第i个源信号到第j个通道的混合衰减系数，si(t)为第i个源信号。利用线性时频变换，(如短时傅里叶变换)，将观测信号变换到时频域中。由于时频变换方法的线性保持特性，观测信号中的各个源分量间的系数关系是不变的，因此，混合信号在时频域中的分布可写为：

(4)

假设在时频点(tk,fk)，只有源si取值非零(其他源幅值较小或为零)，则式(4)可表示为：

(5)

由式(5)可知，在时频域中，对所有属于源sj的时频点(tk,fk)，观测信号[x1(tk,fk)x2(tk,fk)…xm(tk,fk)]的值正比于源si的混合系数[a1ia2i…ami]，因此可以估计出对应源的混合矩阵列向量。通过寻找隶属于不同源信号的时频点x(tk,fk)，则可以准确地估计出完整的混合矩阵。

3　仿真分析

3.1不相关源

以两不相关源信号s1、s2混入两观测信号x1、x2为例，同时混入一定比例的高斯噪声，来说明混合矩阵A的具体估计过程。

(6)

(7)

(8)

利用短时傅里叶变换，将混合信号x1、x2变换到时频域，得到x1(t,f)、x2(t,f)。如果以x1(t,f)、x2(t,f)的实部或者虚部分别作为横、纵坐标画在散点图中，则隶属于不同源信号的时频点(x1(t,f),x2(t,f))将会聚类成相应的直线，两聚类直线的方向向量对应着各源的混合衰减系数，如图1。图1中有两条明显的聚类直线，在散点图中的方向向量分别为[cos(30°)sin(30°)]T、[cos(60°)sin(60°)]T，对应着混合矩阵中的列向量。

图1　散点图Fig.1 The scatter plot

为了能准确地估计聚类直线的方向向量，定义观测信号的频域能量分布为

(I(xi(t,f)))2)dt

(9)

E(f)代表i个传感器接收到的信号在频域的能量和，R(xi(t,f))与I(xi(t,f))为第i个传感器信号在时频变换后的实部与虚部，m为通道数目。两源信号在各自频率处附近，其能量值达到最大，因此可以利用峰值检测法得到对应于各源的频率值fk，如图2中‘*’所示。分别画出时频点(x1(t,f),x2(t,f))在fk的散点图，如图3(a)、(b)所示。然后，将时频点归一化到单位圆，再利用聚类算法估计各自的聚类中心，即为对应的混合衰减系数，如图3(c)、(d)中‘*’所示。图中实线为理想的聚类直线，可以看出两者之间具有较小的偏差，说明本文方法具有较高的矩阵估计精度。

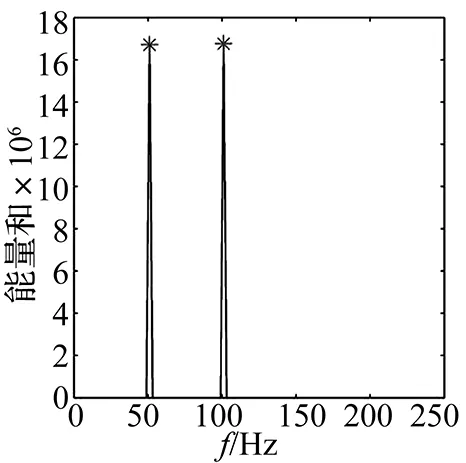
图2　频域能量图Fig.2 The sum energy in frequency-domain

图3　对应峰值点的散点图Fig.3 The scatter plot in peak frequencies

3.2相关源

当各源信号之间具有相关成分时，以上方法将无法有效估计混合矩阵。以3.1节仿真信号为例，在两源信号s1、s2之间加入相关成分c=sin(300πt)，即

(10)

图4　相关源散点图Fig.4 The scatter plot of correlated sources

依然采用相同的混合方式，如式(8)。利用短时傅里叶变换得到观测信号的时频分布，画出二维散点图，如图4。从图中可以看出，相关成分使得散点图中产生了椭圆成分，不具有直线聚类特性，无法利用上述方法估计混合矩阵。同时，相关成分会产生一定的频域能量峰值，也会干扰3.1节中方法的聚类估计过程。因此去掉相关成分的影响，是保证混合矩阵能够被准确估计的关键步骤。

引入文献[8-9]中提出的单源点与多源点的概念，两者定义如下

定义1：如果在某一时频点，仅有一个源存在，那这个点被称为单源点。

定义2：如果在某一时频点，有多个源存在，那这个点被称为多源点。

根据以上定义可知，对于不相关分量所在的时频点，由于只有不相关源存在，因此可以将其视为单源点；对于相关分量所在的时频点，由于有多个源的相关成分存在，因此可以视为多源点。下面通过理论分析，得到单源点与多源点的性质。

将式(8)变换到时频域为

(11)

假设某一时频点(tk,fk)为单源点，即仅有s1(t,f)存在，那么式(11)可写为

(12)

取公式(12)两边的实部与虚部

(13)

(14)

则有下式成立

(15)

(16)

式(15)与式(16)说明，对于单源点，观测信号x1(t,f)、x2(t,f)在时频域中的实部与虚部具有相同的聚类方向，并且与混合矩阵向量一致。

假设某一时频点(th,fh)为多源点，即s1(t,f)与s2(t,f)同时存在，那么式(11)可写为

(17)

对两边同时取实部与虚部，可得

(18)

(19)

为了说明多源点与混合矩阵间的关系，建立以下公式

(20)

(21)

由于混合矩阵为满秩矩阵，因此(a21·a12-a11·a22)≠0。由于已经设定时频点(th,fh)为多源点，因此R(s2(th,fh))与I(s2(th,fh))不可能同时为0。所以，式(20)与式(21)无法同时为0。上述分析说明，对于多源点，观测信号x1(t,f)、x2(t,f)在时频域中的实部与虚部具有不同于混合矩阵列向量的聚类方向。因此提出以下论断：可以通过检测所有时频点在实部与虚部的向量方向是否相同，即

(22)

是否成立，来达到剔除多源点的目的。为验证推论的正确性，对于多源点建立以下公式：

(23)

由于混合矩阵为满秩矩阵，因此(a11a22-a21a12)≠0。式(23)为0的唯一条件是

R(s1(th,fh))·I(s2(th,fh))-

R(s2(th,fh))·I(s1(th,fh))=0

(24)

即来自两个源信号的相关成分具有相同的相位。

式(23)说明，对于多源点，各通道观测信号的实部与虚部的方向向量的关系仅与相关分量的相位有关。当各观测信号xj(t)中所包含的相关分量si(t)具有相同的相位时，即式(24)成立，则式(22)无法有效剔除相关分量的影响。然而大多数情况下，产生于各源信号的相关成分之间的相位关系是随机的，所以满足条件(24)的多源点比例较小，可以被忽略。因此可以认为，产生于各源信号的相关成分之间的相位关系是不同的，即式(24)不成立。因此，可以得出结论：对于多源点，观测信号x1(t,f)、x2(t,f)在时频域中的实部与虚部具有不同的聚类方向。因此，通过判断式(22)是否成立，可以准确地剔除混合信号中的相关成分。多源点的影响被消除之后，则可以按照不相关源混合的处理方式进行矩阵估计。

4　仿真信号分析

4.1仿真信号验证

文献[6]以旋转机械设备的异常振动为模型，给出了仿真信号。借此信号，用于说明本文方法的有效性。假设某旋转机械的基频f0=50 Hz，s1，s2和s3分别对应着不对中、油膜涡动、组件松动等故障信号，并加入一定比例的高斯噪声信号。源信号频谱如图5。

图5　源信号频谱Fig.5 3 Sources in frequency domain

(25)

式中：s1，s2为相关源。混合矩阵为

(26)

信号采样频率为1 024 Hz，共1 024个点。对其进行短时傅里叶变换，由于有3个观测信号，得到三维散点图，如图6。

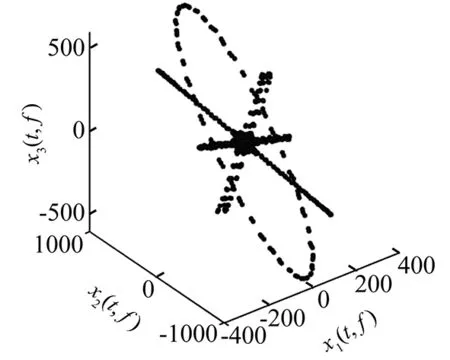
图6　散点图Fig.6 The scatter plot

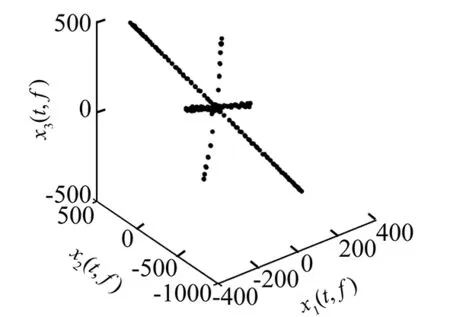
图7　去相关处理后散点图Fig.7 The scatter plot of removing correlated component

图8　本文方法分离信号Fig.8 The separated source using proposed method

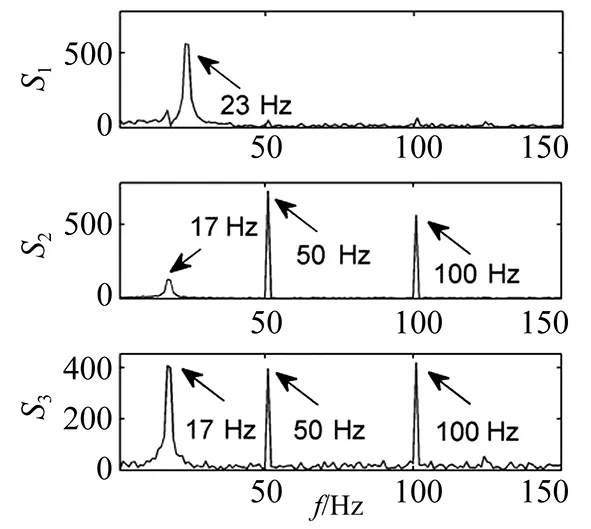
图9　ICA算法分离结果Fig.9 The separated sources using ICA

从图6中可以看出，相关成分使得散点图产生了较为散乱的椭圆成分。去相关成分处理后，散点图如图7。可以看出，剩余的不相关分量具有明显的直线聚类特性，可以准确地估计出混合矩阵。分离信号频谱如图8，可以看出分离信号与源信号频谱特征基本一致，利用式(28)，计算两两之间的相似系数为[0.99 0.98 0.96]。为了对比分析，利用FastICA算法处理混合信号，分离信号频谱如图9。可以看出，仅23 Hz源信号得到了有效地分离，当源信号不满足统计独立特性时，ICA方法无法分离出相关源信号，因此本文方法比ICA算法更适合于相关源信号的分离。

4.2噪声对算法性能的影响

为说明所加背景噪声的大小对本文算法分离结果的影响，引入平均相似系数指标，定量地评价本文方法的分离性能。平均相似系数公式为：

(27)

(28)

1)p≤1。

2)p=1时，表示源信号与分离信号完全相似。

3)p=0时，表示源信号与分离信号相互统计独立。

因此，p越接近于1，说明本文算法的分离结果越好。通过在观测信号中加入不同信噪比的背景噪声，进行盲分离处理后计算p的值，p随噪声比例的变化结果曲线如图10。

图10　相似系数曲线Fig.10 The similarity index

由图10可以看出，低信噪比的噪声会对分离结果造成一定的影响，如在0 dB左右，但相似系数依然大于0.55。随着信噪比的增大，分离结果趋近于1。说明本文算法具有一定的噪声鲁棒性。

5　实验仿真分析

内燃机作为工程领域中重要的动力来源，同时也是主要的振动来源。对于一些大型设备，往往会有多个动力源，因此可以将每一台内燃机视为一个振源进行分析。受限于仅有一台内燃机的实验条件，将内燃机在怠速、额定转速及最高转速这三个常用工况下的振动信号视为3个振源，采用人工混合的方式进行数据分析。因此，分别采集内燃机在这3个转速下的振动信号，采样频率为5 120 Hz，频谱如图11。

图11　3个转速下测量信号Fig.11 The measurement signals

此内燃机为4缸4冲程，其怠速、额定转速及最高转速分别为980 r/min、2 000 r/min、2 400 r/min。通过工况信息，可以计算得出3个转速下的发火基频分别为34 Hz、67 Hz、80 Hz，如图11中所示，由于发火基频处于不同频段，因此可以将其视为不相关分量。同时，各源之间都存在着峰值约为321 Hz左右的宽频成分，因此可以视为相关分量。利用一随机混合矩阵得到3个观测信号。对其进行短时傅里叶变换，得到三维散点图，如图12。

图12　散点图Fig.12 The scatter plot

图13　去相关处理后散点图Fig.13 The scatter plot of removing correlated component

图14　分离信号Fig.14 The separated sources

从图12中可以看出，散点图较为混乱，只有比较模糊的聚类特征，无法用于估计混合矩阵。利用提出的算法进行去相关成分处理之后，散点图如图13。可以看出，图中直线的聚类特性得到了明显地提高，可以更加精确地估计出混合矩阵。利用估计得到的矩阵分离信号，结果如图14，分离信号与源信号间的两两相似系数为[0.94 0.93 0.96]。从分离结果来看，各源信号均得到了有效分离，说明本文方法在处理复杂的实测数据时依然有效。

6　讨　论

本文提出的相关源盲分离算法，是以不相关源盲分离为基础，因此需要保证各个源信号中存在不相关分量，如4.1节中仿真信号s1、s2中的100 Hz与17 Hz分量，以及第5节实测信号中的各个发火基频分量。如果不满足此条件，本文方法将会失效。因此，经过去相关成分处理之后，才可以利用剩余的不相关分量进行矩阵估计，并进行下一步的源信号分离。

7　结　论

实际工程中，不同部件之间产生的振源信号，往往是相关源以及不相关源的混叠，使得传统盲源分离方法无法有效分离出正确的机械振源信号。本文利用信号间的稀疏特性，首先以不相关源为例，提出了有效估计分离矩阵的方法；并理论推导出相关源及不相关源的性质，提出了可以有效剔除相关分量的方法，使得剩余信号可以按照不相关源进行处理。通过仿真信号与实测信号，均验证了本文方法的有效性，具有一定的工程应用价值。

[1] Hyvärinen A, Oja E. Independent component analysis: algorithms and applications[J]. Neural networks, 2000,13(4): 411-430.

[2] Gelle G, Colas M, Delaunay G. Blind sources separation applied to rotating machines monitoring by acoustical and vibrations analysis[J]. Mechanical Systems and Signal Processing, 2000, 14(3): 427-442.

[3] Peled R, Braun S, Zacksenhouse M. A blind deconvolution separation of multiple sources, with application to bearing diagnostics[J]. Mechanical Systems and Signal Processing, 2005, 19(6): 1181-1195.

[4] Kerschen G, Poncelet F, Golinval J C. Physical interpretation of independent component analysis in structural dynamics[J]. Mechanical Systems and Signal Processing, 2007, 21(4): 1561-1575.

[5] Yang Y, Nagarajaiah S. Output-only modal identification with limited sensors using sparse component analysis[J]. Journal of Sound and Vibration, 2013, 332(19): 4741-4765.

[6] 周晓峰, 杨世锡, 甘春标. 相关机械振源的盲源分离方法[J]. 振动与冲击, 2010, 31(14): 60-63.

ZHOU Xiao-feng, YANG Shi-xi, GAN Chun-biao. Blind source separation of statistically correlatedsources[J]. Journal of Vibration and Shock, 2012,31(14):60-63.

[7] 孟宗, 蔡龙. 基于EEMD子带提取相关机械振动信号单通道盲源分离[J]. 振动与冲击, 2014 33(20): 40-46.

MENG Zong, CAI Long. Blind source separation of single-channel statistically correlated mechanical vibration signals based on subband extraction of EEMD[J]. Journal of Vibration and Shock, 2014 33(20) 40-46.

[8] Reju V G, Koh S N, Soon I Y. An algorithm for mixing matrix estimation in instantaneous blind source separation[J]. Signal Processing, 2009, 89(9): 1762-1773.

[9] Dong T, Lei Y, Yang J. An algorithm for underdetermined mixing matrix estimation[J]. Neurocomputing,2013,104(15):26-34.

Blind source separation of correlated vibration sources

YU Gang1, ZHOU Yiqi1, ZHANG Weifen2

(1. Key Laboratory of High-efficiency and Clean Mechanical Manufacture, Ministry of Education, Shandong University, Jinan 250061, China; 2.Unit 72850 of PLA, Jinan 250032, China)

The conventional blind source separation(BSS) method, independent component analysis(ICA), may not separate correlated vibration sources. However, most vibration sources generated in different structures are correlated, they may cause failure of ICA. Here, a new BSS method capable of separating correlated vibration sources was proposed. It was divided into two steps. Firstly, it was needed to remove the correlated components, and then the reminder components were regarded as uncorrelated sources to be processed. Theoretical analysis, simulation and tests were employed to validate the effectiveness of the proposed method.

blind source separation; vibration sources; correlated sources

国家科技支撑计划(2015BAF07B04);国家自然科学基金(51475277)

2014-12-16修改稿收到日期：2015-03-19

于刚 男，博士生，1987年12月生

周以齐 男，教授，1957年1月生

TN911.7;TH165.3

A

10.13465/j.cnki.jvs.2016.15.036