题海无边 寻根是岸

☉江苏省大丰高级中学 李素梅

题海无边 寻根是岸

☉江苏省大丰高级中学 李素梅

当下的数学教学越来越多的是做题、讲题，随着竞争压力的加大和知识难度的加深，有时候教师没有精力去研究教学的有效性，只能以不断训练的方式去寻求知识的熟练度和考点的广度.从一定程度上来说，这种训练模式必不可少，但是效率稍低.从这么多试题训练来看，有些是重复训练，而有些问题则是因为没有找到普遍性而让教学变得无目的性，因此笔者认为在做到一定量训练的同时，还需要将同类型的问题进行归纳、总结、研究，将具备共同属性背景知识的数学问题找到其根源所在，即所谓题海无边，寻根是岸.

近年来，愈来愈多的考题具备了一定的高等数学的背景，这些背景决定了数学问题的考查需要找到它们共同的知识核心——题根.寻找同类型问题的题根成为有效解决数学难点问题的重要核心.无论从心理层面还是知识层面来说，掌握数学问题的题根有足够的教学效果：其一，将同类型问题进行合理归类，设计成专题型知识处理，因为只有这些比较困难的试题才会以专题形态进行处理，整合在同一类型的专题中有助于学生不断研究共性，获得教学的高效率；其二，对于在题海中不断寻找具备共性的、具备高等数学知识背景的数学难题，将学生的思维调动起来，既提高教师自身专业化的水平，也提高了学生解决难题的有效性.笔者以向量教学中具备高等数学背景的极化恒等式为例，结合案例谈一谈寻找数学问题题根的教学设计.

案例1 向量复习教学——极化恒等式.

学习目标：（1）借助极化恒等式解决向量与三角、立体几何的综合问题；（2）掌握数形结合的思想方法.

教学重点：如何合理地用极化恒等式解决数量积.

教学难点：向量与三角问题，向量与空间立体几何问题的转化.

设计意图：“根本法”教学就是要学生真正从心里重视课本，研究课本，掌握最常规最实用的解题方法.平面向量的数量积常常在高考题中以小题的形式出现，且此类试题常见的解法有几何法和坐标法.综观近几年数学高考，向量试题有着越来越综合、越来越灵活的趋势，因而解题方法和解题工具的选择显得尤为重要，选择不恰当，费时、费力，且不得要领；选择恰当，题目可以“秒杀”.而极化恒等式恰恰就是可以“秒杀”这类高考向量题的一个有力工具.

一、寻找本质

提出问题：同学们，大家有发现a·b与a+b，a-b之间的关系吗？a·b=______________.

设计意图：根据向量数量积的运算律，同学们应该不难发现非零向量a，b的数量积与它们的和、差之间存在着这样的等量关系：a·b=［（a+b）2-（a-b）2］.引入本课主题.

极化恒等式：设a，b是2个非零向量，则成立恒等式a·b=［（a+b）2-（a-b）2］，也可写成4a·b=（a+b）2-（a-b）2.

几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的，即a·b=

设计意图：给出极化恒等式的定义，通过几何意义加深对这个公式的理解.对知识的扩充，并不是增加负担，而是对数学知识的理解，着力于选择解题工具.

二、研究共性

案例2 设△ABC，P0是边AB上一定点，满足P0B=AB，且对于边AB上任一点P，恒有则判断三角形的性质为_______________（.填直角三角形、等腰三角形等）

图1

0只有AC=BC时才能成立.

设计意图：此题考查的是平面向量的线性运算和数量积运算，是一个常规考题，但由于涉及动点变化的不等式恒成立，致使难度增大.考生普遍反映该题无从入手，得分较低.所以利用极化恒等式把多变量问题最终转化为单变量问题，解答就非常简单了.虽然此题也可用坐标法解答，但如何建系，设点，学生处理能力比较弱，即使建立了坐标系，对含参变量的恒成立问题，学生无法解答.解法如下：

图2

三、类题巩固

案例3 已知a·b=0，向量c满足（c-a）·（c-b）=0，|ab|=5，|a-c|=3，则a·c的最大值为_______.

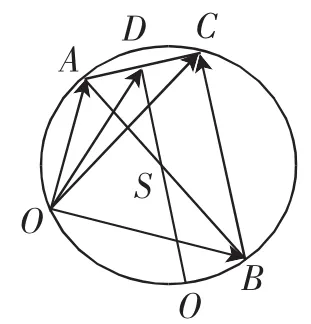
图3

变式：怎样求a·c的最小值呢？

设计意图：刚刚结束的一模考试中，此题得分偏低，考后学生反映该向量题很难，不知从何入手去正确选择解题策略，原因在于无法解读题干信息透露的真实意图.利用极化恒等式后，把a·c的最大值转化为的最大值，即圆上动点O到弦AC中点D的距离的最大值，这样就容易多了.设计变式，有助于促使学生产生体验新的知识的深切体会，有助于促成学生形成看待原有问题的全新视角，提炼数学思想方法，提高各种数学能力.本题也可以用其他方法解决，如几何法和坐标法，但学生的切入点找不好.

图4

白鹤滩水电站库区巧家县垫高造地区砂土液化分析……………………………………………………… 李德周（9-40）

解法3：（坐标法）如图5建系，令C（0，0），O（x，y），则由直角三角形BCA可知，A（0，3），B（4，0）.所以a=（-x，3-y），b=（4-x，-y），a·b=x2+y2-4x-3y=0，a·c=x2+y2-3y=4x，x∈，即得a·c≤18.

图5

四、节外生枝

案例4 正方体ABCD-A1B1C1D1的棱长为2，MN是它的内切球的一条弦（把球面上任意两点之间的线段称为球的弦），P为正方体表面上的动点，当弦MN最长时，的最大值为__________.

解析：当弦MN最长时就是球的直径，也就是正方体的棱长，取MN的中点为O，利用极化恒等式知，而O为球的直径的中点即球心，也是正方体的中心，所以点P为正方体的顶点时|取到最大值，所以的最大值为2.

变式：改求取值范围呢？

设计意图：将向量和空间立体几何综合起来，运用“极化恒等式”同样可以“秒杀”.

五、推本溯源

研究用极化恒等式“秒杀”这类高考向量试题，是让大家多一个解决向量试题的工具，并不是追求高难度的解题技巧，而是着意于解题工具的选择，着意于数学问题的理解，揭示问题的本质，看出试题背后隐藏的高等数学背景.向量有很多这样的几何背景，诸如向量加减法、向量数乘、平面向量基本定理、向量数量积公式所涉及的投影，这些都是值得我们去思考、去设计的.从这样的教学设计中，笔者也在深深地思考对于教学我们更应该去做的.

（1）在题海战术比较普遍的今天，教师更需要专研具备共性问题的价值，这些对于学生来说既解决了学生最为困扰的问题、大大提高了教学的实效，也脱离了一味题海训练模式的枯燥性，将专题型题根式教学与一定量训练结合的复习教学方式，才是教学合理的方向.

（2）专题题根式教学具备实效性，以文中向量极化恒等式为例，笔者认为在近年应试教学中有着极大的用武之地，但是每年都会有新的热点出现，将这些知识系统的整理、研究出来，有助于教师自身成长，也有助于当下教学的有效性.即所谓题海无边，寻根是岸.

1.赵思林.关于高考数学创新型试题的立意［J］.中学数学教学参考（上），2009（1-2）.

2.宋卫东.从生“动”到生动，诠释思维品质的提升［J］.中学数学月考，2013（5）.

3.鲍建生.向量变式教学研究［J］.数学教学，2013（11）.