基于Dijkstra算法最短路问题C语言实现
张淑敏 王元芬
(1.青海师范大学数学系 西宁 810008)(2.虎台中学 西宁 810008)
基于Dijkstra算法最短路问题C语言实现
张淑敏1王元芬2
(1.青海师范大学数学系西宁810008)(2.虎台中学西宁810008)
在日常生活和生产中最短路问题是重要的优化问题之一,而Dijkstra算法是目前公认的解决最短路径问题较好的算法。论文采用C语言编程来实现使用Dijkstra算法求解最短路问题。
最短路问题; Dijkstra算法; C语言
Class NumberTP301.6
1 引言
在日常生活和工作中,为了取得最大的利益或者节约更多的成本,人们都在试图用最简单的方法找出尽可能短的路程到目的地,例如铺设管道中为了节约成本而规划最合理的铺设方法,出门旅游选择合适的出游路线和出游方式等。这些问题都可以划归为最短路径问题,尽可能快地计算最短路径是我们生活的迫切需求。求最短路有两种算法,一是求从某一点到其他各点之间最短距离的Dijkstra算法,二是求网络图上任意两点之间最短距离的矩阵算法[2]。本文主要解决最短路径的Dijkstra算法的计算,利用其思想编写计算机程序,辅助完成最短路径问题的求解[4]。并且进一步熟悉最短路径问题的Dijkstra算法,掌握其思想,并会利用其算法解决一些优化问题。在用C语言编程中,体会利用简单语句就可以解决复杂问题的好处。
2 基本知识
2.1Dijkstra算法
Dijkstra算法是由E.W.Dijkstra于1959年提出,又叫迪杰斯特拉算法,它应用了贪心算法模式,是目前公认的最好的求解最短路径的方法。算法解决的是有向图中单个源点到其他顶点的最短路径问题,其主要特点是每次迭代时选择的下一个顶点是标记点之外距离源点最近的顶点。
2.2最短路径问题
最短路径问题是指若网络中的每条边都有一个数值(长度、成本、时间等),则找出两节点(通常是源节点和阱节点)之间总权和最小的路径就是最短路径问题。最短路径问题是网络理论解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。最短路径问题有三种具体形式:单源最短路径、全局最短路径和两点最短路径。
单源最短路径,包括确定起点的最短路径问题,确定终点的最短路径问题(与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题。在无向图中该问题与确定起点的问题完全等同,在有向图中该问题等同于把所有路径方向反转的确定起点的问题。)全局最短路径,求图中所有的最短路径。两点最短路径,即已知起点和终点,求两结点之间的最短路径[5]。
2.3C语言程序设计基础知识
C语言是一种结构化模块化的程序设计语言,它由顺序结构、选择结构、循环结构三种基本结构组成,使用这三种结构可以解决任何复杂问题[3]。常用的选择结构和循化结构的语句如下:
2.3.1选择结构和循环结构
1) if语句和用if语句构成的选择结构:
· 语句形式:if(表达式)语句。
· 执行过程:执行if语句时,首先计算紧跟在if后面一对圆括号中的表达式的值。如果表达式的值为非零(“真”),则执行其后的的if子句,然后去执行if语句后的下一条语句;如果表达式的值为零(“假”),则跳过if子句,直接去执行if语句后的下一条语句[9]。
2) for语句和用for语句构成的循环语句
· 语句形式:for(表达式1;表达式2;表达式3)循环体
· 执行过程:
(1)计算表达式1;
(2)计算表达式2;若其值为非零,转步骤(3);若其值为零,转步骤(5);
(3)执行一次for循环体;
(4)计算表达式3;
(5)结束循环[9]。
2.3.2主要函数及其函数的调用
1) 主要函数
(1)printf函数
· 调用形式:printf(格式控制,输出项1,输出项2,…)。
说明:输出格式说明的作用是将要输出的数据按照指定的格式输出。格式说明由%符号和紧跟其后的格式描述符组成。除了格式转换说明外,字符串中的其他字符(包括空格)将按原样输出[9]。
(2)scanf函数
· 调用形式:scanf(格式控制,输入项1,输入项2,…)。
· 说明:格式控制的主要作用是指定输入时的数据转换格式,即格式转换说明。scanf的格式转换说明与printf类似,也是由%开始,其后是格式字符。输入项之间用逗号隔开,对于int、float和double型变量,在变量之前必须加&符号作为输入项[9]。
2) 函数的调用
· 函数的一般调用形式:函数名(实在参数表)
· 说明:一个实用的C语言源程序总是由许多函数组成,这些函数都是根据实际任务,由用户自己来编写。但是一个C语言源程序无论包含多少个函数,正常情况下总是从main函数开始执行,main函数结束,所以在C语言中经常调用函数无完成某个命令。被调用函数有自定义的函数,也有C语言头文件中包含的,但绝对不能是main函数,因为main函数不能被其他函数调用。
3 Dijkstra算法的C语言实现
3.1算法描述[10]
将源点到其他各个点的路径转化为有效矩阵;路径的距离填入到矩阵对应的i行j列,自己到自己点的距离为0,其他没有路径关系的,距离为T。
将求最短路的问题转化为求距离矩阵d[i][j]中按照如下规律求数据和的最小值,算法描述如下:
1) 给源点P标号P[0]=0,给其他各点T标号T[k]=d[0][k],表示源点到其他各点的距离,并把这些点的P标号临时记为P[k]=0;
2) 在所有T标号中选出最小者,将其改为P标号改为P[i]=T[i];
3) 重新计算具有T标号的其他各点T[k],选出T[k]和P[i]+d[i][k]中较小者作为新的T标号T[k];
4) 重复步骤2)、3),直到除源点外其他各点的P标号都不是0为止,这时P[k]是从源点到k点的最短距离。
具体Dijkstra算法解决最短路问题步骤如下:
步骤1:给源点V0标上P标号d(V0)=0,表示V0到V0的距离为0,V0为起点,给其它点标上T标号d(Vj)=l0j(j=1,2,…,n);
步骤2:在所有的T标号中取出最小者d(Vj)=l0j,则把该点的T标号改为P标号;
步骤3:重新计算具有T标号的其他各点,选出d(Vk)+l0j中较小者作为Vk的新的T标号;
一般情况下,S={Vj|Vj具有P标号},U={Vj|Vj具有T标号},令d(Vk)=min{d(Vj)}为点的P标号,于是,vk∈S把U中的点的T标号修改为min{d(Vj),d(Vk)+lk}。
步骤4:重复步骤2、3,直到Vn∈S,这时d(Vn)是从V0到Vn的最短距离,最短路径可通过将所有路径方向反转一步步确定前一个点来确定。这个算法经过n-1次循环必结束。
3.2C语言程序代码
#include〈stdio.h〉
#define T /* 点i到点j没有路径关系的,距离为T*/
#define N /* 点的个数 */
intd[N][N];
void fun()
{int i,j;
printf(“ 请输入:”);
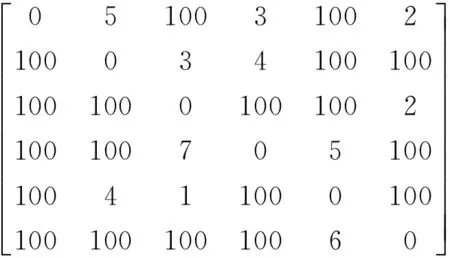
for(i=0;i {for(j=0;j scanf(“%d,”,&d[i][j]);/*将源点到其他各点的路径转化为有效矩阵输入*/ } } main() {intP[N],T[N],q[N]; int min,i,j,k,s; i=0; fun(); for(j=0;j P[j]=0; /*标记各点的临时P标号*/ for(k=1;k T[k]=d[0][k]; /*标记各点的T标号*/ while(i {min=T; for(k=1;k {if(P[k]==0) {for(j=0;j if(T[k]>P[q[j]]+d[q[j]][k])/*重新计算具有T标号的其他各点*/ T[k]=P[q[j]]+d[q[j]][k]; if(T[k] {min=T[k]; s=k; } } } P[s]=min; /*把T标号中选出的最小者改为P标号*/ q[i++]=s; printf(“
0点到%d点的最短距离为:%d”,s,P[s]); } } 3.3最短路问题实例 下面举例说明算法的执行过程及结果: 例:求下图中自点0到其他各点的最短有向路。 图1 实例图示 令T=100,N=6 程序结果为 0dao5dezuiduanluwei:2 0dao3dezuiduanluwei:3 0dao1dezuiduanluwei:5 0dao2dezuiduanluwei:8 0dao4dezuiduanluwei:8 所以0点到5点的最短距离为2,最短路径为0-5; 0点到3点的最短距离为3,最短路径为0-3; 0点到1点的最短距离为5,最短路径为0-1; 0点到2点的最短距离为8,最短路径为0-1-2; 0点到4点的最短距离为8,最短路径为0-3-4。 最短路径问题这一重要问题早在20世纪初就已经得到人们的高度重视,当时也有许多科学家研究这一问题的求解方法。但直到1959年荷兰计算机科学家Dijkstra才给出这一问题求解的基本思想,并给出了算法。使用Dijkstra算法不仅能解决最短路问题,还能解决许多实际问题而且在解决图论问题中被认为是好算法。使用Dijkstra算法解决实际问题时,设计相应的C语言程序,此程序比较直观,简单有效,可使大部分同学容易理解,应用非常广泛。 [1] 刁在筠.运筹学[M].北京:高等教育出版社,2010:203-206. DIAO Zaijun. Operational Rresearch[M]. Beijing: Higher Education Press,2010:203-206. [2] 施泉生.运筹学[M].北京:中国电力出版社,2008:177-179. SHI Quansheng. Operational Rresearch[M]. Beijing: China Electric Power Press,2008:177-179. [3] 苏智雄,等.基于CPM原理和Dijkstra算法的SPM网络计划模型及性质[J].运筹与管理,2008,17(1):148-153. SU Zhixiong. Network planning model and properties of dijkstra algorithm based on the principle of CPM and SPM. 2008,17(1):148-153. [4] 张勤.Dijkstra最短路径算法的C语言实现[J].福州大学学报,2011,4:24-27. ZHANG Qin. The shortest path dijkstra algorithm with C program[J]. Journal of Fuzhou University,2011,4:24-27. [5] 徐俊明.图论及其应用[M].北京:中国科学技术大学出版社,2010:1-22. XU Junming. Graph Theory with Applications[M]. Beijing: University of Science and Technology of China Press,2010:1-22. [6] 熊德国.用Dijkstra算法求解最短路的矩阵方法[J].河南理工大学学报(自然科学版),2011,30(5):608-615. XIONG Deguo. The method of matrix with dijkstra algorithm to solve the most short problem[J]. Journal of Henan University of Technology,2011,30(5):608-615. [7] 代西武.Dijkstra矩阵算法[J].北京建筑工程学院学报,2007,23(2):65-72. DAI Xiwu. Dijkstra Matrix Algorithm[J]. Journal of Beijing Institute of Civil Engineering and Construction,2007,23(2):65-72. [8] 黄保和,等.数据结构教程(C语言版)[M].北京:水利水电出版社,2000. HUANG Baohe. Data structure course(C language version)[M]. Beijing: Water Conservancy and Hydropower Press,2000. [9] 田淑清,等.全国计算机等级考试二级教程——C语言程序设计[M].北京:高等教育出版社,2011. TIAN Shuqing, et al. C language programming[M]. Beijing: Higher Education Press,2011. [10] KyleLoudon.算法精解[M].北京:机械工业出版社,2012. KyleLoudon. Algorithms extract solution[M]. Beijing: Mechanical Industry Press,2012. Realization of the Shortest Path Problem with C Program Based on Dijkstra Algorithm ZHANG Shumin1WANG Yuanfen2 (1. Department of Mathematics, Qinghai Normal University, Xining810008)(2. Hutai Middle School, Xining810008) The shortest path is one of important optimized problems in our daily life and production. At the same time, Dijkstra algorithm is a better one recognized as solving the shortest path problem. In the paper, Dijkstra algorithm is used to solve the shortest path problem by C program. the shortest path problem, Dijkstra algorithm, C program 2016年2月6日, 2016年3月17日基金项目:国家自然科学基金(编号:11461054)资助。 张淑敏,女,硕士,教授,研究方向:计算智能及其应用。 TP301.6 10.3969/j.issn.1672-9722.2016.08.001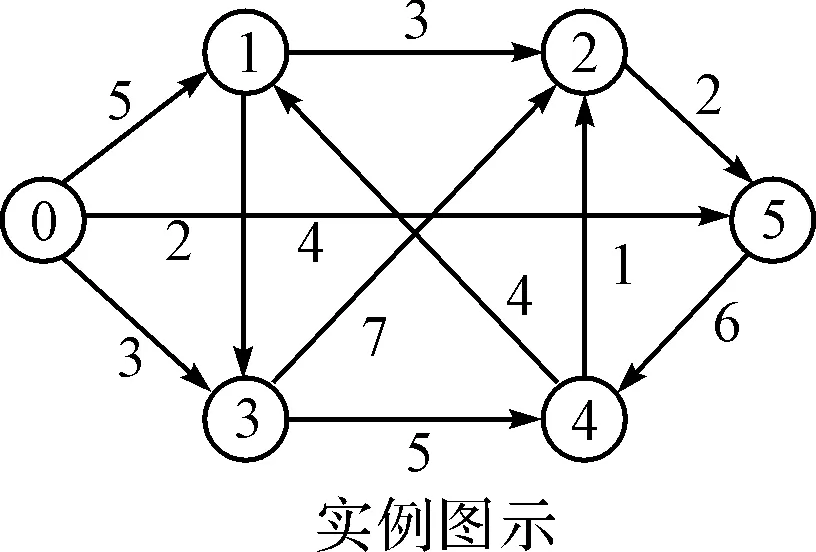
4 结语

