递推最小二乘法在变压器绕组参数辨识中的研究应用

党　琪　张江滨

(西安理工大学　西安　710048)



递推最小二乘法在变压器绕组参数辨识中的研究应用

党琪张江滨

(西安理工大学西安710048)

变压器是电力系统最重要的电气设备之一,根据绕组变形进而引起的绕组漏电感参数变化这一特征,故对绕组参数在线辨识提出了更高的要求。论文利用双绕组变压器模型,采用递推最小二乘算法,对绕组的漏电感参数进行辨识。通过Matlab/SIMULINK对某一简单的系统的仿真，结果表明该算法不受负载率及其功率因数的影响，能够准确地识别变压器绕组参数，对绕组状态进行在线监测。

变压器; 递推最小二乘法; 参数辨识

Class NumberTM41

1　引言

在日常运行过程中，变压器不可避免地要遭受故障时短路电流引起的电磁力冲击，绕组的匝间故障已经上升至事故率的首位，可能使绕组局部或整体发生变形，从而使变压器无法正常运行[1～2]，根据变压器的构造特征，绕组的漏感是由绕组结构所决定的,对于一台变压器而言,其绕组发生了变形,几何尺寸随之发生变化时,其漏感值也要产生变化。基于模型保护的变压器保护原理需要对变压器参数进行准确的在线辨识,将变压器绕组的漏电感,电阻做为变压器内部故障的检测特征量,以根据其变化判断变压器是否发生故障。因此，变压器的参数辨识越来越重要，文献[3～6]对变压器绕组参数辨识主要采用最小二乘法,最小二乘法的收敛较慢,影响保护的速动性。文献[7～8]采用智能算法中粒子群算法对变压器的参数进行辨识,但智能算法所占用储存空间大,计算速度较慢。

本文在建立变压器模型并通过数学公式推导,通过在Matlab/SIMULINK中仿真，利用递推最小二乘算法对简单系统中的变压器参数进行在线辨识，通过负荷一定，功率因数改变及功率因数一定，负荷率的改变对算法进行验证，为变压器绕组是否存在变形提供依据。

2　变压器模型

2.1双绕组变压器等值模型

本文以单相双绕组变压器为例,如图1所示。

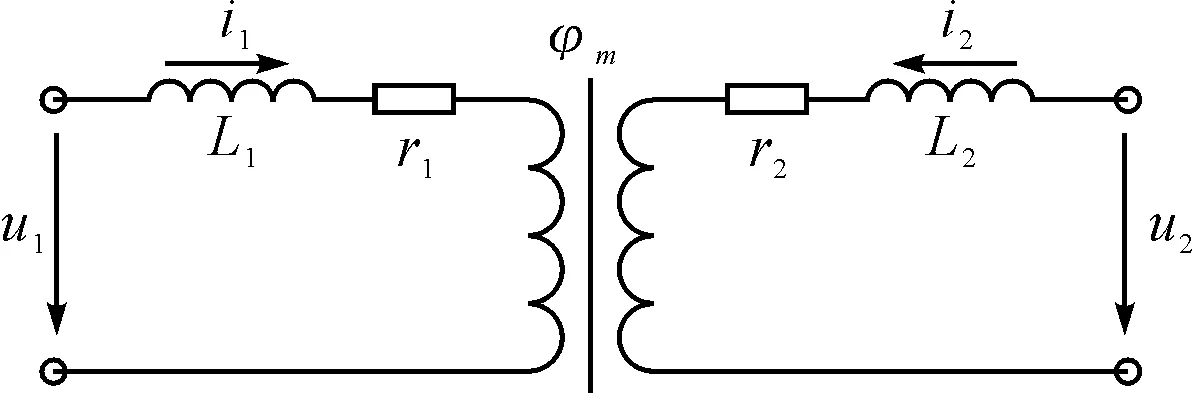
图1　双绕组单相变压器等值电路

根据变压器原、副边等值回路方程可得:

(1)

式(1)中u1、u2、i1、i2分别是变压器原副边电压和电流,r1、r2和L1、L2分别是变压器一、二次绕组的电阻和漏感,k1、k2分别为变压器一、二次绕组的匝数,φm是变压器铁心主磁通。令变压器变比K=k1/k2,dφm/dt为原、副边绕组间的互感磁通。式(1)中项包含了B-H曲线的非线性关系,很难直接获得。消去得到回路平衡方程为

(2)

由变压器模型得到,涉及到变压器模型中的参数是:变压器绕组的电阻,漏电感和励磁电感。其中原副边的电压电流量均可由变压器两侧的互感器测得,故其电阻电感值的精度影响甚大。

2.2Y0/Δ接法的三相双绕组变压器

本文建立模型以三相双绕组为例,对称的三相Y0/Y0变压器可由单相变压器回路方程模型可直接推广到,对于Y0/Δ接法的变压器,二次侧相电流不易直接获得,需进行处理,如图2所示。

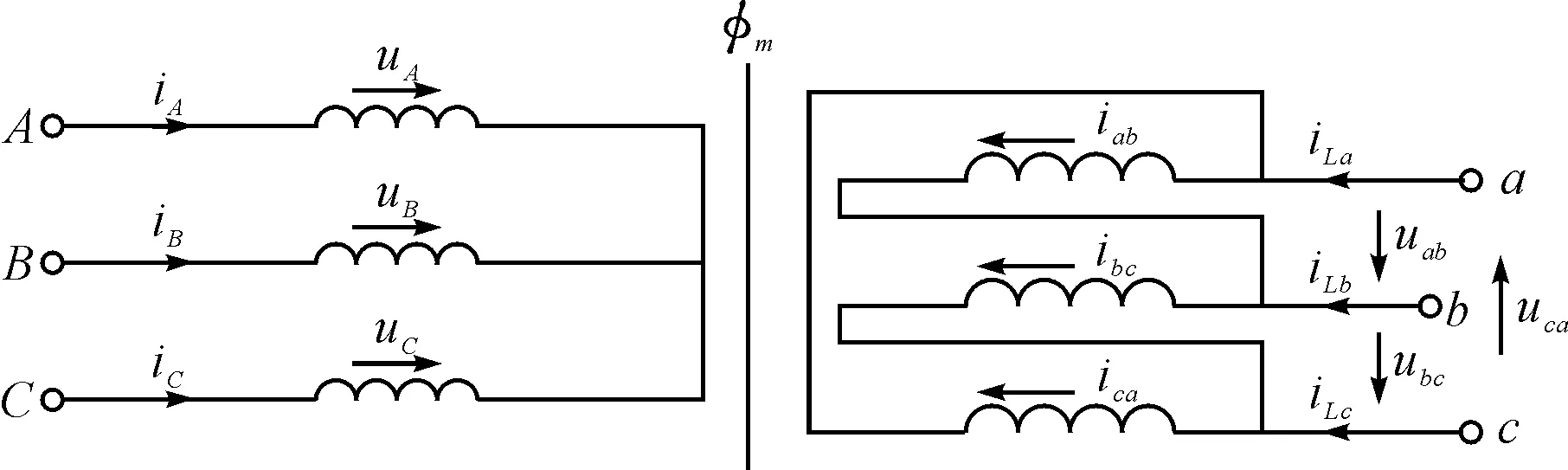
图2　三相双绕组变压器的Y0/Δ接法模型

式中,uA、uB、uC为原边侧的三相电压;iA、iB、iC为原边侧的三相电流。uab、ubc、uca为副边侧绕组三相电压;iLa、iLb、iLc为副边侧绕组三相线电流;ia、ib、ic为副边侧绕组的相电流。

原边一次侧回路方程为

(3)

副边二次的侧绕组的回路方程为

(4)

变压器回路平衡方程是以绕组中的电压、电流为基础建立的,对于电流互感器接在△侧绕组出线上的情况,绕组相电流不能直接测量得到。根据电路原理三角形接法线电流与相电流之间的关系有:iab-ica=iLa,ibc-iab=iLb,ica-ibc=iLc,以及三相变压器绕组对称的特点有式(5):

LA=LB=LC=L1,Lab=Lbc=Lca=L2

rA=rB=rC=r1,rab=rbc=rca=r2

(5)

Y0/Δ三相变压器的回路方程可以变换为式(6)所示:

(6)

同理,原边侧Y0接法绕组回路方程可以变化为式(7)所示:

(7)

得到Y0/Δ接法变压器的回路平衡方程为式(8)所示:

(8)

由上式可知,变压器正常运行,励磁涌流以及发生外部故障时,变压器结构不发生变化,式(8)均成立,而当外部内部故障时,变压器内部结构发生了变化,上式不成立。因此,当绕组发生变形后,漏感值同时变化的特点,可将变压器绕组的漏感值作为特征量,以其是否发生变化判断变压器绕组是否发生故障,故本文主要对漏电感参数进行在线辨识。

3　参数辨识

3.1参数辨识原理

参数辨识是指已知模型结构,从而进行参数估计,其过程是通过实验数据来确定模型中的未知参数。

变压器作为本文研究的主要内容,参数的辨识利用变压器的等效电路,通过测量变压器原副边上的电压和电流值,得到变压器绕组的参数,而这些参数是通过数学模型进行求解,为典型的灰箱系统。电力系统中的参数辨识具有“灰箱”系统的典型特征,即对系统有一定了解,知道模型或待测参数,其数学建模是根据电力系统的基本原理进行,利用系统辨识方法求解待辨识的参数。为了辨识变压器的参数,需要先定义上述的参数,在定义参数时应考虑以下三个方面:

1) 测量值能够确定变压器的主要参数并反映工作特征

变压器绕组的电阻、电感等参数可以作为待识别的参数，可反映变压器的固有特性，以及结构和材料的工作性能。而电压、电流及磁通等参数不能反映变压器的固有物理特性，只影响了算法。

2) 模型需符合实际工作特性

变压器在工作频率为f=50Hz时，杂散电容可以忽略，T型等效电路模型和变压器的磁路模型能够反映变压器。

3) 采用的测量数据需符合变压器特点

在对变压器进行参数辨识的时候,需要对变压器两侧的电压和电流进行测量,作为辨识模型中的已知参数。电压和电流值都是通过互感器进行测量的,互感器固有的传变特性会对辨识的结果带来一定的误差。

3.2最小二乘法

最小二乘法(又称最小平方法)是一种数学优化技术。优点在于能够避免噪声的统计知识,在大多数情况可得到参考解,且拥有较好的统计特性。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。其基本结构有两种形式,一种是经典的一次完成算法;另一种是现代的递推算法。前者在理论研究方面更为方便,后者更适用于计算机的在线辨识。最小二乘法的原理如下:

设一单输入单输出系统,用如下随机差分方程描述为式(9):

yk+a1yk-1+…+anyk-n

=b1uk-1+b2uk-2+…+bnuk-n+ξk

(9)

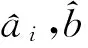
当有N+n对输入输出数据时,可以写出N个方程组,n为每个方程组总方程的个数,方程描述为式(10):

(10)

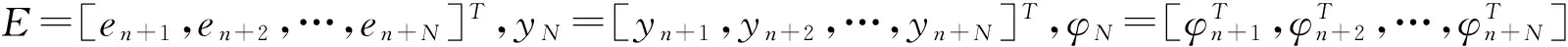
(11)

3.3递推最小二乘法

采用递推最小二乘法辨识参数θ(对应于待辨识的L1,L2,R1,R2),其递推步骤如式(12):

(12)

RLS用作在线实时辨识是有缺陷的:随着数据的增长,将出现“数据饱和”现象。即数据饱和就是随时间的推移,采集到的数据越多,新数据所提供的信息被淹没在老数据中,失去算法的修正能力。这时参数估计值偏离真值较远无法更新;对于时变过程来说,它又将导致参数估计值不能跟踪时变参数的变化。遗忘因子法能有效避免“数据饱和”现象。基本思想是对老数据加上遗忘因子,用来降低老数据的信息量,提升新数据的有效性,其递推法如式(13)所示:

(13)

遗忘因子通常不小于0.9,如果过程是线性的,应选0.95≤λ≤1。遗忘因子如果选的太大将会降低算法的跟踪性能,太小将易受噪声影响。

3.4变压器绕组参数辨识

变压器在运行过程中达到稳定状态时,电力系统中稳态电压、电流都是频率为50Hz的正弦波,将式(1)离散化后得到辨识方程:

(14)

其中

根据辨识模型的标准式,则超定线性方程组为

[S]n×4[X]4×1=[Y]n×1

(15)式中,矩阵X为待辨识的4维向量,[X]=[R1,L1,R2,L2]T等式左边的N*4矩阵为输入量S，即为可直接测量得到的双端绕组电流的导数；等式右侧N*1的已知矩阵Y为输出量，即为测量得到的双端绕组的电压量。以变压器电流的导数作为输入量，等式左边的量为输出量，各侧绕组的漏感、电阻作为待辨识的参数，就构成了辨识模型。

通常,上式中的辨识量为四个,但辨识方程只有两个,由可辨识理论可知,可辨识的参量只有两个,将会造成输入矩阵|STS|=0,参数的不可辨识。变压器绕组变形通常引起漏电感变化，故在辨识中通常对漏电感参数进行辨识，而绕组电阻受温度的影响较大，变形对其影响较小，故将其作为已知量，减少待辨识的数目。

4　仿真验证

本文使用Matlab/SIMULINK仿真软件搭建某一简单系统进行仿真,验证该算法有效性及正确性。通过上述章节的分析进行编程,所搭建系统模型图如图3所示。

图3　系统模型图

在上图所示的仿真模型中,电源通过输电线路、变压器向负荷供电在模型的搭建中,用三个相同单相变压器组合成一个三相变压器,接线方法采用Y0/Δ-11方式。对于每一个单相变压器,参数设定如下:高压侧绕组漏感为0.017H,低压侧绕组漏感为0.014H,即短路电感值为0.031H。变压器的端口电压电流取自两侧的电压电流互感器。SIMULINK搭建的仿真模块如图4所示。将SIMULINK中A相所测量得到的电气量,经过M文件进行递推最小二乘法的辨识。

图4　SIMULINK仿真图

利用改进最小二乘法辨识高压侧漏电感L1和低压侧漏电感L2,对各个电压、电流分别采用选取3000个采样点,进行参数辨识,变压器绕组正常时,辨识结果如图5所示。

图5　三相辨识图

从图5中的(b)、(c)中可以看出，可以分别地辨识出三相高低压侧的漏电感值，辨识值接近初始值，并在初始值附近波动且递推辨识的结果呈一条直线状，趋于平稳,说明递推辨识的结果是准确稳定的。

为了更准确地验证算法的正确性，估测最大误差。本文通过负载率一定，功率因数从0.6～1时进行参数辨识以及通过负荷功率因数一定,负载率从100%～30%变化时对三相漏感参数进行辨识，如表1所示。辨识值与原始值结果如图6、图7所示。

表1　负载率一定,功率因数对参数辨识结果的影响

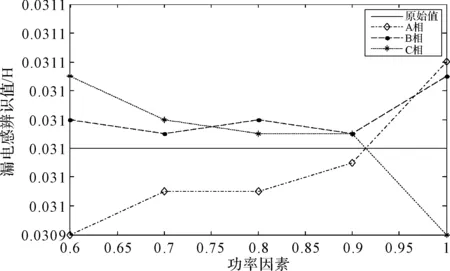
图6　功率因数对辨识结果的影响

由图6及图7可得，负载率一定时，辨识结果的最大误差为-0.19%；功率因数一定时，辨识结果的最大误差为0.2%。说明该算法不受辨识结果及其负载率的影响，收敛较快，因此可以准确地对变压器进行参数辨识，从而判断绕组是否发生形变。

图7　负载率对辨识结果的影响

5　结语

本文通过变压器的辨识方程,采用递推最小二乘法对变压器的参数进行辨识,通过在Matlab/SIMULINK中进行简单建模仿真,仿真的结果表明,递推最小二乘法可以有效准确地辨识变压器的参数,误差较小,且最小二乘算法对白噪声具有滤波作用,具有较好的工程应用,可以实时地实现对变压器绕组状态的监测。

[1] 李朋,张保会,郝治国,等.基于电气量特征的变压器绕组变形监测技术现状与展望[J].电力自动化设备,2006,26(2):28-32.

LI Peng, ZHANG Baohui, HAO Zhiguo, et al. Current status and Prospect of transformer winding deformation monitoring technology based on the characteristics of electrical capacity[J]. Power Automation Equipment,2006,26(2):28-32.

[2] 杨启平,邓正文,董辉,等.基于最小二乘法的电力变压器参数辨识算法[J].上海电力学院学报,2012,28(5):401-405.

YANG Qiping, DENG Zhengwen, DONG Hui, et al. Parameter identification algorithm of power transformer based on least square method[J]. Journal of Shanghai University of Electric Power,2012,28(5):401-405.

[3] 高晶,王建华,张保会,等.变压器漏电感参数在线辨识方法研究[J].西安交通大学学报,2008,2:202-203.

GAO Jing, WANG Jianhua, ZHANG Baohui, et al. On line identification method of leakage inductance parameters of transformer[J]. Journal of Xi’an Jiao Tong University,2008,2:202-203.

[4] 王果,朱大鹏.变压器绕组变形在线监测算法的改进[J].广西电力,2005(2):31-33.

WANG Guo, ZHU Dapeng. Improved online monitoring algorithm of transformer winding deformation[J]. Guangxi Electric Power,2005(2):31-33.

[5] 袁佳歆,袁剑,钟永恒.基于漏抗分析的变压器绕组变形在线检测方法研究[J].电工技术学报,2014(S1):170-176.

YUAN Jiayun, YUAN Jian, ZHONG Yongheng. On line detection method of transformer winding deformation based on leakage reactance analysis[J]. Journal of Electrical Engineering,2014:(S1):170-176.

[6] 熊小伏,邓祥力,油波.基于参数辨识的变压器微机保护[J].电力系统自动化,1991,23(11):18-21.

XIONG Xiaofu, DENG Xiangli, YOU Bo. Transformer microcomputer protection based on parameter identification[J]. Automation of Electric Power Systems,1991,23(11):18-21.

[7] 杨浩,曾鑫,罗建.基于约束最小二乘法的变压器三相漏感辨识算法[J].电力系统自动化,2009(13):68-72.

YANG Hao, ZENG Xin, LUO Jian. Transformer three phase leakage inductance identification algorithm based on constrained least square method[J]. Automation of Electric Power System,2009(13):68-72.

[8] 高亮,陈亚杰,邓祥力.基于粒子群优化算法的变压器参数辨识[J].上海电力学院学报,2014(2):17-19.

GAO Liang, CHEN Yajie, DENG Xiangli. Parameter identification of transformer based on particle swarm optimization algorithm[J]. Journal of Shanghai University of Electric Power,2014,2:17-19.

[9] 徐大可,汲胜昌,李彦明.变压器绕组变形在线监测的理论研究[J].高电压技术,2000,26(3):38-43.

XU Dake, JI Shengchang, LI Yanming. Theoretical study on the online monitoring of transformer winding deformation[J]. High Voltage Technology,2000,26(3):38-43.

[10] 王世山,汲胜昌,李彦明.电缆绕组变压器短路时线圈轴向稳定性的研究[J].中国电机工程学报,2004,24(2):166-170.

WANG Shishan, JI Changsheng, LI Yanming. Study on the axial stability of the short circuit of the cable winding transformer[J]. Proceedings of the Electrical Engineering of China,2004,24(2):166-170.

[11] 刘兴平,陈民铀.一种配电变压器绕组变形故障的在线监测新方法[J].电力系统保护与制,2013(12):20-26.

LIU Xingping, CHEN Minyou. New online monitoring method of distribution transformer winding deformation[J]. Power System Protection and System,2013(12):20-26.

[12] 邓祥力,熊小伏,高亮,等.基于参数辨识的变压器绕组变形在线监测方法[J].中国电机工程学报,2014,34(28):4950-4955.

DENG Xiangli, XIONG Xiaofu, GAO Liang, et al. On line monitoring method of transformer winding deformation based on parameter identification[J]. Proceedings of the Electrical Engineering of China,2014,34(28):4950-4955.

[13] 李朋,张保会,郝治国,等.基于回路平衡方程的变压器绕组变形在线监测研究[J].电力自动化设备,2006,26(5):11.

LI Peng, ZHANG Baohui, HAO Zhiguo, et al. On line monitoring of transformer winding deformation based on loop balance equation[J]. Electric Power Automation Equipment,2006,26(5):11.

[14] 欧小波,汲胜昌,彭晶,等,漏电抗的参数辨识技术在线监测变压器绕组变形的研究[J].高压电器,2010,46(12):41-45.

OU Xiaopo, JI Shengchang, PENG Jing, et al. The research on the transformer winding deformation by the parameter identification technology of leakage reactance[J]. High Voltage Electrical Equipment,2010,46(12):41-45.

[15] 王明林,陈民铀,赖伟,等.一种改进的配电变压器短路电抗在线检测方法[J].电力自动化设备,2015,35(3):41-15.

WANG Mingli, CHEN Minyou, LAI Wei, et al. An improved online detection method of short circuit reactance of power distribution transformer[J]. Power Automation Equipment,2015,35(3):41-15.

[16] 索南加乐,王志恩,焦在滨.基于变压器T形等效电路的漏电感参数特性分析[J].电力自动化设备,2010,34(11):38-42.

SUO Nanjiale, WANG Zhien, JIAO Zaibin. Leakage inductance parameter characteristic analysis based on T equivalent circuit of transformer[J]. Electric Power Automation Equipment,2010,34(11):38-42.

[17] Behjat V, Vahedi A, Setayeshmehr A, et al. Diagnosing shorted turns on the windings of powertransformers based upon online FRA using capacitiveand inductive couplings[J]. IEEE Transactions on Power Delivery,2011,26(4):2123-2133.

[18] Kornatowski E, Banaszak S. Diagnostics of atransformer’s active part with complementary FRA andVM measurements[J]. IEEE Transactions on Power Delivery,2014,29(3):1398-1406.

Application of Recursive Least Squares Method in Transformer Winding Parameter Identification

DANG QiZHANG Jiangbin

(Xi’an University of Technology, Xi’an710048)

Transformer is one of the most important electrical equipments in power system. With the characteristic of leakage inductance change caused by winding deformation, on-line parameters identification of transformer winding is put forward higher requirements. In this paper, double winding transformer modelis simulated and the least square method is adopted to realize accurate on-line identification of the transformer parameters. The simple system is simulated by Matlab/SIMULINK and the resultis shows that the algorithm is not affected by the load factor and power factor. The algorithm can identify the transformer winding parameters accurately and achieve on-line monitoring.

transformer, least square method, parameter identification

2016年2月10日,

2016年3月15日

党琪,女,硕士,研究方向:电力系统测量、控制与保护。张江滨,男,博士,研究方向:电力系统运行与控制。

TM41

10.3969/j.issn.1672-9722.2016.08.008